乘波体压缩面变化对其气动性能影响分析1)
崔 凯徐应洲 肖 尧 李广利
(中国科学院力学研究所高温气体动力学国家重点实验室,北京100190)
(中国科学院大学工程科学学院,北京100049)
乘波体压缩面变化对其气动性能影响分析1)
崔 凯2)徐应洲 肖 尧 李广利
(中国科学院力学研究所高温气体动力学国家重点实验室,北京100190)
(中国科学院大学工程科学学院,北京100049)
乘波体是一种利用激波包裹特性获得高升阻比的高速飞行器构型.已有研究中,乘波体气动性能的改善主要依赖于给定源流场条件下的前缘型线优化.本文采用数值优化和计算流体力学模拟为主要手段分析了乘波体压缩面变化对其气动性能的影响,以期有效拓展乘波体的设计空间.主要内容如下:首先给出了一种基于表面局部变形的乘波体设计方法.其次结合运用增量修正参数化方法、计算流体力学分析和微分演化算法构造了乘波体压缩面外形气动优化设计流程,以一种椭圆锥形流场生成的乘波体作为基准构型开展了无黏优化.之后从优化结果中选择升阻比递增的6个典型构型进行前缘钝化处理后,基于N-S方程对其气动性能进行了评估.最后综合依据无黏/黏性计算结果分析了乘波体压缩面变化对其气动性能的影响.结果表明该部分形状的改变对乘波体气动性能影响十分明显,在升力面积不变的条件下,乘波体压缩面形状变化可导致其升阻比出现成倍变化,即使在升力不减条件下,升阻比较基准构型也可获得超过14%的提升.此外,还可导致乘波体相对压心系数出现明显偏移.
乘波体,优化设计,增量参数化方法,微分演化算法,计算流体力学
引言
目前高超声速飞行器的气动布局主要包括升力体、轴对称旋成体、翼身融合体和乘波体等几类[1],其中乘波体[2-4]是一种较为独特的构型概念.该构型基于给定流场,通过激波面切割和流线追踪方式设计.在设计飞行条件下(给定马赫数、攻角等),高速飞行时产生的弓形激波完全附着于飞行器的边缘,上下表面没有流动泄露,激波后高压区可完全包裹于飞行器的下半部分,使飞行器升阻比有效提升.因飞行时好像乘在激波之上,故称为“乘波体”.近年来,随着高超声速飞行器相关研究的不断升温,有关乘波体的各类研究也逐渐成为热点之一.
由于乘波体可基于任意超声速流场生成,因而源自不同流场的乘波体设计方法和性能分析是主要研究内容之一.早期工作主要围绕一些相对简单的源流场,如正圆锥流场[5]、倾斜圆锥、椭圆锥及带有纵向曲率的旋成体流场[6-8]、楔锥流场等[9].近年来,随着数值模拟技术的不断发展,一些更加复杂的流场,如任意截面锥形体流场[10-11]、卡门曲线为母线的旋成体流场[12]和多级压缩锥体流场[13]等亦被用于生成乘波体.在密切锥类方法基础上,也进一步发展了密切流场法[14]和密切内锥设计方法等[15-16].此外,近期还有直接对锥体及其流场进行切割的被动乘波体设计方法[17-18].上述研究均在不同程度上改善了乘波构型的综合性能.在此基础上,以乘波体为基础的创新构型和高超声速飞行器新概念也不断涌现[19-25],这意味着乘波体已逐渐开始从单纯的概念研究逐渐向实用化阶段推进.
伴随乘波体相关研究的深入,气动外形优化也逐渐成为此领域重要研究内容.这一领域的研究始于20世纪60年代.最具代表性的工作为 Bowcutt等[26]和Corda等[27]于1987年和1988年分别针对圆锥流场和幂次率母线轴对称体流场生成的乘波体,采用参考温度法计算摩擦阻力,并以非线性单纯形算法作为优化驱动器对前缘线进行优化,获得了一系列“黏性优化乘波体”.基于类似的优化流程,后续工作通过结合使用不同的乘波体设计方法及不同优化方法,特别是现代启发式算法,将这一研究由单目标优化逐渐拓展至多目标优化设计[19-20,28-32].
依据其设计流程,乘波体由其源流场和位于激波面上的前缘线共同确定.从目前公开发表文献看,乘波体的外形优化均在给定源流场条件下,通过改变前缘线形状进行优化设计,对乘波体下表面(即压缩面)形状的研究相对较少.由于乘波体压缩面为迎流面,是乘波体升力和阻力的主要来源,因此其外形变化必然会导致乘波体气动性能的大幅改变.文献[33-34]以黏性优化乘波体为基础,分别采用风洞实验和计算流体力学方法对两个前缘线俯视形状相同,但压缩面具有明显差别的乘波体进行了气动性能分析,结果表明两种构型的升阻比差别超过5%,该文结果表明乘波体压缩面的形状变化对其气动性能的影响不可忽略.因此,对压缩面形状的合理设计以及优化问题进行分析和研究,对拓展乘波体及乘波飞行器的设计空间,获得气动性能更为优良的乘波体无疑具有积极意义.但从研究现状看,这一方向的工作尚未看到公开文献发表.
本文主要基于上述背景,从应用基础研究角度出发,以椭圆锥导乘波体为实例,开展了乘波体压缩面变化对其气动性能的影响研究.具体工作内容简述如下:首先对给定前缘线条件下(等价于升力面积不变)乘波体压缩面合理设计问题进行了分析,在此基础上基于超声速流场扰动仅向下游传播的特点,给出了一种基于表面局部变形的乘波体构型设计方法.之后以无黏优化设计和黏性分析作为手段,分析了乘波体压缩面形状变化对其气动性能的影响.结果表明,即使在考虑黏性及钝化条件下,乘波体压缩面的变化也可导致其升力、阻力、升阻比和压心等参数出现大幅改变.
1 乘波体压缩面设计问题分析
1.1 源自给定流场的乘波体方法简介
源于给定流场的乘波体设计方法在相关文献中已有较多介绍[8-13],此处仅进行简单阐述.乘波体生成流程如图1所示.首先,给定一个任意三维几何体作为生成体,在设计条件下,应用数值求解欧拉方程可获得其无黏流场,同时捕捉到激波面;其次,在激波面上定义一条三维曲线,即乘波体的前缘线;随后,从前缘线上的每一点出发,沿来流方向进行流线追踪,所有流线构成的曲面做为乘波体的下表面(压缩面);最后,采用自由流面方法设计乘波体上表面并完成设计.由于流面上没有法向流动,因而在设计条件下,乘波体下表面的绕流流场与源无黏流场一致,同时由于乘波体的前缘线精确位于激波面上,下表面经压缩激波后产生的高压区不会泄露到上部,因此可保证其良好的气动性能.

图1 乘波体设计流程图示Fig.1 Sketch of waverider construction
1.2 给定前缘线条件下乘波体压缩面设计问题分析
从前述乘波体的设计流程中不难看出,乘波体的外形主要由两个因素确定:(1)生成乘波体的源流场,(2)位于激波面上的前缘线.源流场给定后,激波面可唯一确定,如何在激波面上合理选择前缘线,即前缘线优化问题已有较多研究.然而,源流场与激波面并非一一对应,即同一激波面可能对应多个源流场,图2基于二维图示对此进行说明.当给定某一圆锥及来流条件时,可获得激波面形状.假定将圆锥母线从中间某一位置开始进行有限幅度的上弯或下弯,如图2中虚线所示,由于前半部分仍保持锥体外形,因此激波面仍将与初始圆锥相同,但波后流场不同.此时,当在此激波面上给定相同的前缘线时,基于不同的流场中也会必然获得下表面(压缩面)形状迥异的乘波体构型.由于乘波体压缩面为迎流面,其外形的变化必然导致乘波体的气动性能产生明显差异.

图2 具有相同激波面的源几何体Fig.2 Generating bodies with the same shock layer
由上可知,乘波体压缩面的变化等价于改变生成乘波体的源流场.依据这一思路,虽然可以基于前述乘波体设计流程来逐次修改其压缩面外形,但将大幅增加流程的复杂性,同时,如果考虑源几何体的三维局部变形,源流场的求解只能依赖于三维计算流体力学分析,这也将带来计算消耗的大幅增加.此外,采用这一思路是将乘波体的参数化间接采用源几何体的参数化替代,这也增加了参数化方法选择和设计空间界定的难度.针对上述问题,本文基于超声速流场的特点,采用表面局部变形方法生成乘波体,并基于增量修正方法进行参数化.
2 基于表面局部变形的乘波体修正方法和增量参数化设计
乘波体的设计马赫数一般在高超声速区域,在此条件下,流场中的扰动仅向下游传播,且扰动范围限于激波锥之内.乘波体一般为扁平体,当压缩面的中后部分区域产生有限幅度的外形变化时,若能合理限制变形区域和幅度,其对流场所产生的扰动将不会干扰乘波体的边缘区域,因此其乘波特性,即激波附着边缘及高压区包裹特性将不会受到破坏,可生成新的乘波体外形.显然,采用这样的乘波体生成方式,可大幅简化前述分析和优化流程.
由于乘波体压缩面为流面,无法解析表达,若采用样条曲面对其进行拟合,设计参数个数及各设计参数的控制区域均难以控制.基于上述情况,本文采用增量修正方法[25]进行参数化设计.简而言之,该方法是将外形的参数化转化为其修正量的参数化,并在网格坐标系统下将修正量叠加至原有外形,数学表达式如下
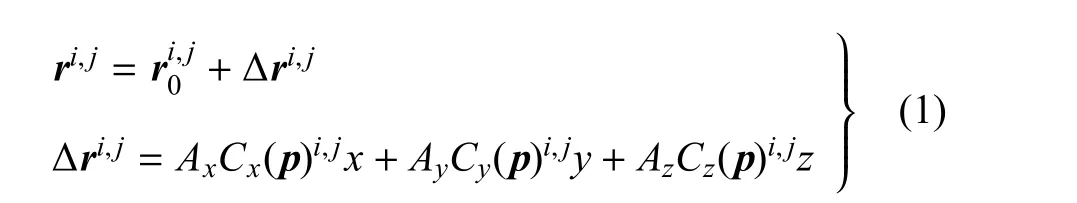
式中,i和j分别为控制域内的面网格点编号为控制域内基准外形网格点的三维空间坐标向量,Δri,j为该点坐标修正量向量,ri,j为修正后的该点外形坐标值向量.Ax,Ay和Az分别为3个空间坐标方向的最大增量值,Cx,Cy和Cz分别对应3个方向的控制函数,p为3个方向控制函数的参变量集,实际中作为设计变量使用.图3给出了一个实例,图中,左侧上下两图分别为初始外形和修正量形状,右侧为叠加后的外形.
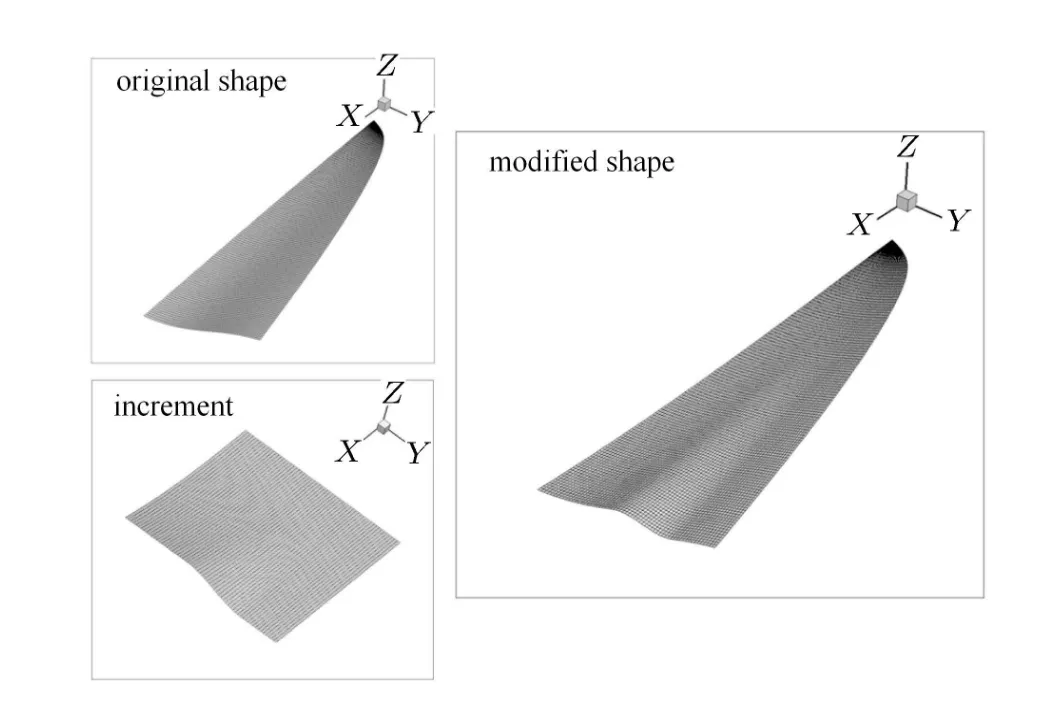
图3 外形参数化实例Fig.3 An example of shape parameterization
基于本文问题的特点并从缩减计算量的角度考虑,参数化主要针对乘波体压缩面的对称(轴向)和尾缘(展向)剖面的两条边界曲线,乘波体前缘线固定不变.沿轴向的控制函数曲线采用广义抛物线进行参数化,其归一化的表达形式为
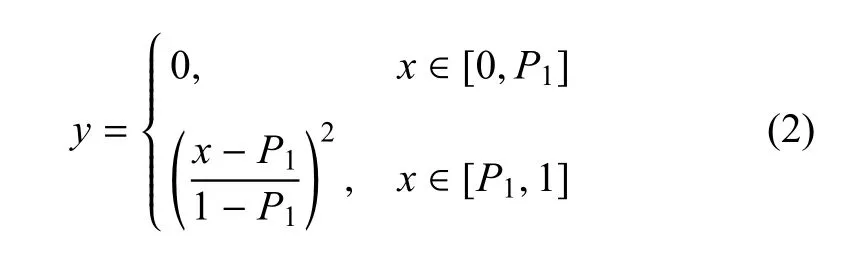
其中,P1为直线段与曲线段的交接点,在优化设计中作为设计变量.沿展向的控制函数曲线采用广义余弦函数进行参数化,其归一化的表达形式为
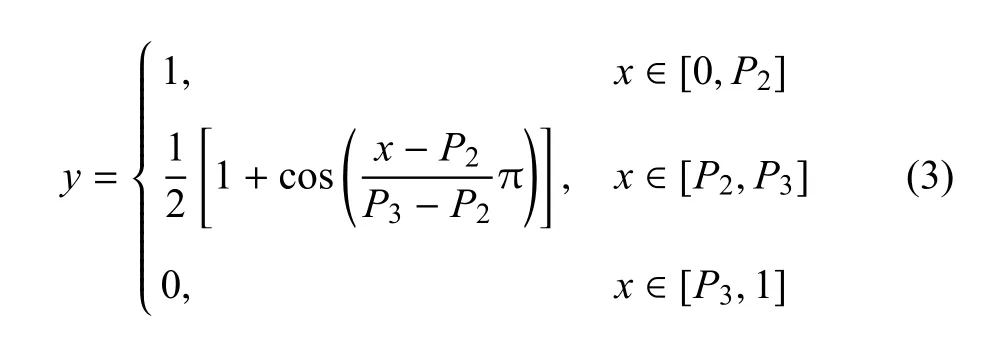
其中,P2和P3为余弦曲线两端直线段与曲线段的交接点,在优化设计中作为设计变量.此外,修正量的外形基于边界线的变化插值获得.采用上述参数化方法,通过参数P1和P3的合理选择,可保证变形区域距离边界保留足够距离,进而保证乘波体压缩面边缘区域不发生变形,保持其乘波特性.
3 乘波体压缩面无黏优化和结果分析
基于优化设计分析乘波体压缩面形状变化对其气动性能的影响,可在设计空间内获得充足的研究样本.优化设计基于无黏分析进行,其主要原因如下:(1)依据设计原则,乘波体仅在尖前缘及无黏条件下方可完全保证其乘波特性,因而基于无黏计算可严格测试前述基于局部表面变形的乘波体生成和参数化设计方法;(2)基于无黏分析可大幅缩减计算量及提高优化流程的鲁棒性.后续计算中,自由来流条件均给定为飞行马赫数6和高度25km.
3.1 基准乘波体构型及性能参数
基准乘波体构型采用基于任意锥体流场的乘波体外形设计软件包 GCBWRG[10],源于截面长宽比为1.618的椭圆锥体流场生成.长度给定为2m,其上表面为水平自由来流面.图4给出了飞行攻角0°条件下乘波体沿轴向不同截面压力分布云图.可以看出,高压区均完全包裹于乘波体的下方,乘波性能良好.图5绘出了该乘波体升阻比随飞行攻角的变化曲线,考虑底部阻力时,0°攻角下的升阻比为5.65,最大升阻比出现于2°攻角状态,数值为6.55,对应升力系数Cl=0.06235(以俯视投影为参考面积,其数值为1.4492m2).
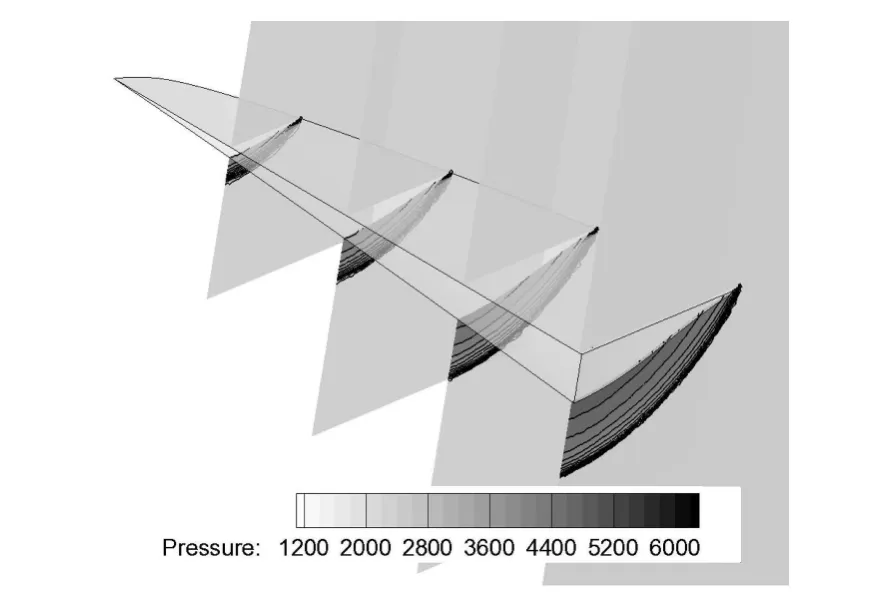
图4 基准乘波体(半模)及其截面压力分布Fig.4 Baseline waverider(half model)and its pressure contours at dif f erent cross section
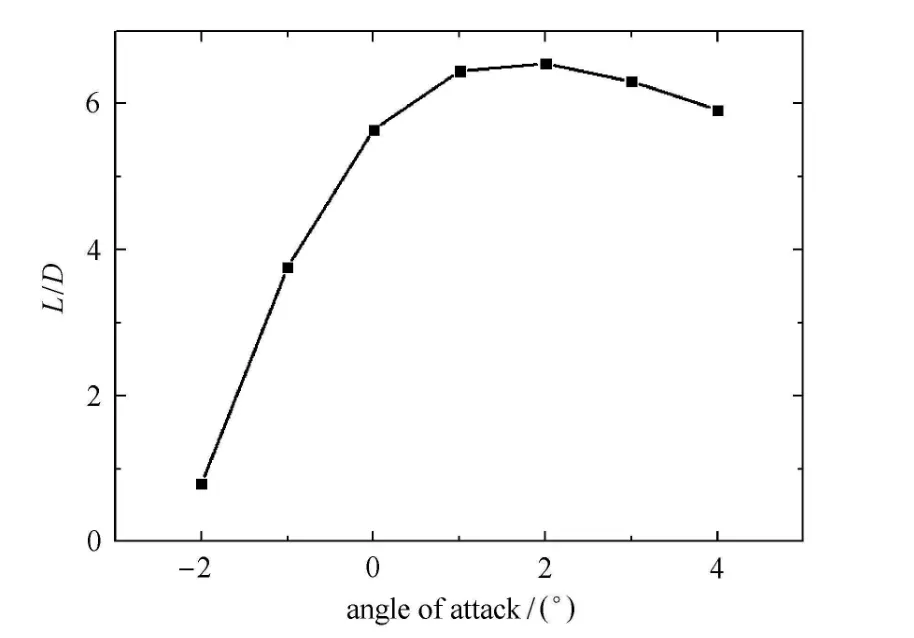
图5 基准乘波体升阻比随攻角变化曲线Fig.5 Variation of the lift-to-drag ratio values with fligh angle of attack for baseline waverider
3.2 优化目标和流程
优化目标给定为升阻比最大化,同时将升力系数不减作为不等式约束.优化模型的数学表达式为
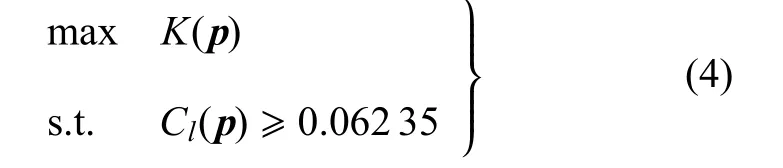
式(4)中,p为设计变量构成的矢量,K为升阻比,Cl为升力系数.将约束条件采用采用惩罚函数法处理并进行归一化后,式(4)的约束优化问题可转化为如下的无约束优化问题
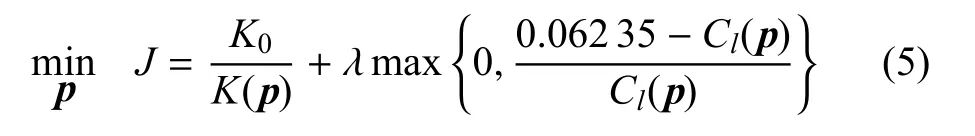
式 (5)中,K0为基准乘波体的最大升阻比 (K0=6.5),λ为惩罚因子,这里固定取为100.采用归一化表达的目的为避免升阻比和升力系数间的数值不匹配.
优化设计的设计变量共5个,包括外形最大增量值(控制外形变化量)、式(2)和式 (3)中的参数P1~P3(控制外形变化区域和形状),以及飞行攻角.上述5个参数及其给定的上下边界如表1所示.表中,Hmax为最大增量值,α为飞行攻角(度).
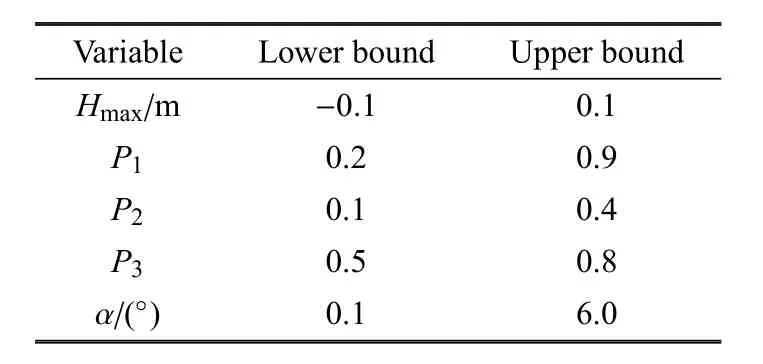
表1 设计变量的上下边界Table 1 Boundary values of design space
优化算法采用微分演化算法[35],该方法属于进化类算法的一种,主要思路为从一个初始种群出发,经过变异、交叉、遗传等操作来获得目标函数的最优值.该方法与遗传算法的思路相似,具有不需要计算目标函数的梯度,鲁棒性强,全局最优值搜索能力较强等优点.同时,由于该方法直接采用实数编码,且在染色体的交叉选择及种群更新等方面的处理优于遗传算法,因此更加高效.优化算法的流程图如图6所示.

图6 微分演化算法流程图Fig.6 Flowchart of dif f erential evolution algorithm
3.3 优化结果及分析
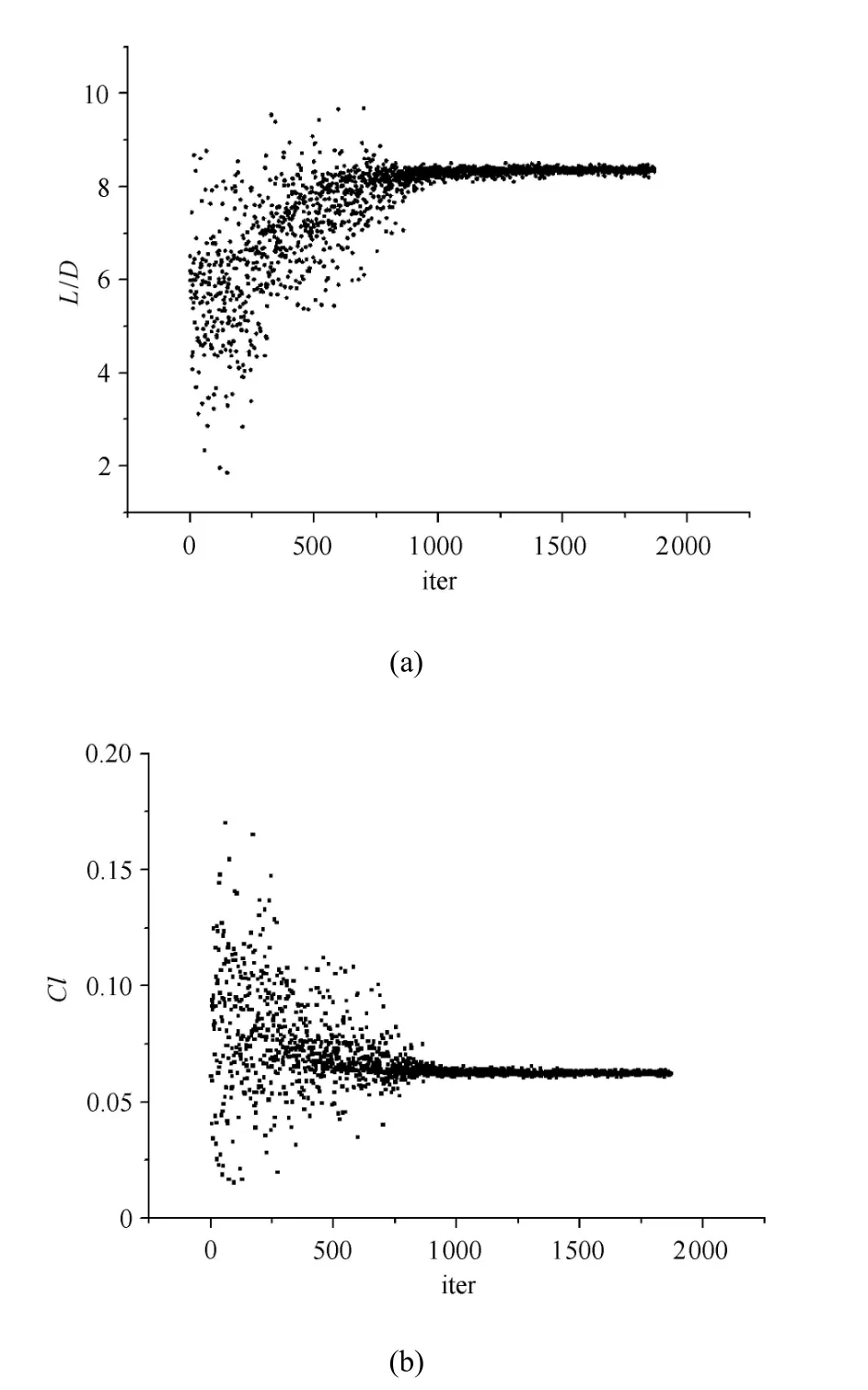
图7 升阻比(a)和升力系数(b)收敛图Fig.7 Convergence history of theL/D(a)and the lift coefficient(b)
图7分别给出了优化目标(升阻比)和约束(升力系数)随迭代进行的历程.经优化后,乘波体的最大升阻比为8.39,较基准构型提升29.1%,升力系数为0.06248,略高于基准构型的升力系数(0.2%).上述结果表明通过压缩面优化,可在满足升力系数不减条件下有效改善乘波体的升阻比.此外,整个优化历程中的升阻比最大值为9.69,较基准构型提升近50%,但其升力系数仅为0.04042,不满足约束条件,这表明升力约束为紧约束.
为评估本文乘波体生成方法的有效性,从所有优化算例中遴选出变形量达到上下边界值,即向上(图8(a))和向下(图8(b))变形幅度最大的两个构型进行验证.图8分别给出了上述两个构型在设计条件下(0°飞行攻角)的不同截面压力分布云图.从图中可以看出,两个乘波体构型的压缩面形状具有较大差别,但在设计状态下,高压区仍完全包裹于飞行器下部,即乘波特性明显保持.图9给出了上述两个构型乘波体尾缘处(X=2m)的截面压力分布与基准乘波体的等值线图比较,图中左半部分均为基准乘波体,右半侧分别为构型A和构型B,为清晰表达,仅给出激波面附近的压力等值线(2200Pa~3200Pa).从图中可见,经压缩面变形后,两个乘波体的激波面均与基准外形激波面保持一致.上述结果充分表明了前述乘波体生成方法的有效性.
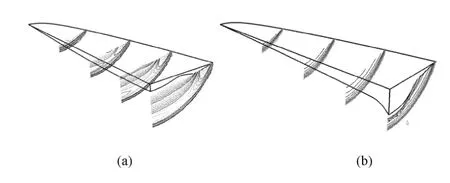
图8 两种乘波体的不同截面压力云图Fig.8 Pressure contours at dif f erent cross-sections of the two waveriders
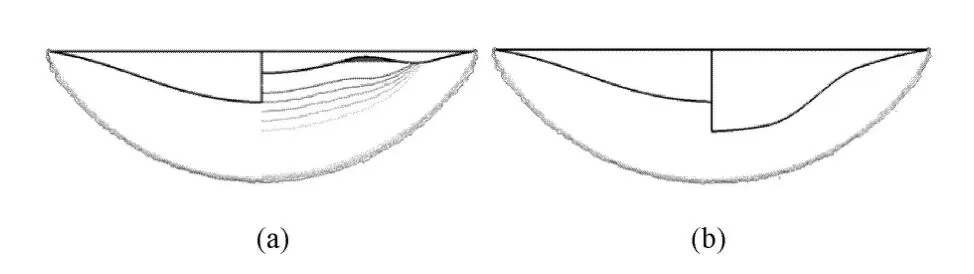
图9 乘波体尾缘压力等值线比较Fig.9 Pressure contours comparison at the ending edge
两个构型的设计变量数值及设计条件下的主要气动参数结果如表2所示.从表中可以看出,两个构型的最大变形量(Hmax)分别达到上下边界.从气动参数比较看,二者的升力系数差别约为7倍,阻力系数差别达20倍以上,升阻比亦有接近4倍的差距.相对压心变化也超过一倍.上述结果表明压缩面的形状改变可导致乘波体的气动性能出现大幅变化,设计空间获得极大拓展.此外,结果还表明乘波体与高升阻比并不等价,若压缩面选择不当,尽管构型具有乘波特性,但亦可能导致其升阻比大幅下降.
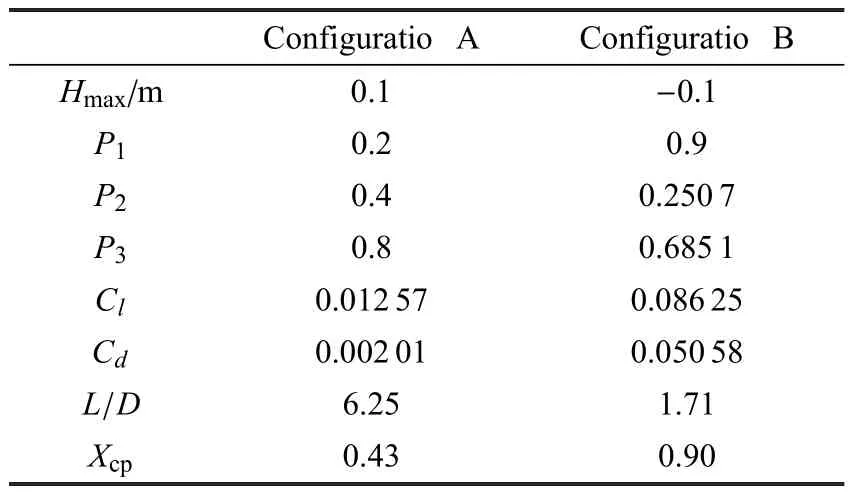
表2 两种边界构型的设计变量和气动参数值Table 2 Values of design variables and aerodynamic parameters of the two configuration
4 考虑黏性和边缘钝化的典型构型评估
基于前述的无黏优化设计结果,对于本文算例而言,乘波体压缩面的设计空间可得到基本界定.为进一步分析,从前述优化结果中选择具有不同升阻比的 6个典型构型 (无黏升阻比变化范围为2.87~7.86),采用加材料方法对其边缘进行厚度为10mm的钝化处理,所得外形如图10所示.之后基于N-S方程对上述构型的气动性能进行了数值评估.

图10 典型构型外形图Fig.10 Geometries of typical waverider configuration
计算网格采用多块结构网格,见图11.为保证可比性,所有算例均基于相同的网格拓扑结构和网格参数,总网格数为232万,贴近壁面的网格进行了加密处理,近壁首层网格尺度为0.2mm,以保证边界层的捕捉.计算采用总变差减小格式,时间推进选用隐式格式,采用k-ε湍流模型.

图11 钝化前缘乘波体黏性分析计算网格示意图Fig.11 Grid structure for viscous analysis of blunt-edge waveriders
在设计状态(飞行攻角0°)下,上述乘波体尾缘截面压力分布云图与基准构型的比较如图12所示.图中左侧部分均对应基准构型,右侧部分对应前述6种典型构型.从图12可以明显看出,尽管由于钝化和黏性的影响,前缘激波出现脱体,下表面高压区有部分泄漏,但所有构型的激波位置、激波面附近压力分布及上表面附近的压力分布均与基准构型保持一致,即经表面局部变形后的构型所具有的乘波特性与基准构型相同.该结果再一次验证了本文提出的乘波体生成方法的有效性.
表3列出了上述6种典型构型及基准乘波体构型的黏性/无黏气动性能评估结果.表中Cl为升力系数,Cd为阻力系数,L/D为升阻比,Xcp为纵向相对压心系数.C0表示基准乘波体构型(黏性评估时亦对边缘进行了钝化),C1~C6与图10中给出的构型对应,α为飞行攻角.由于无黏优化过程中该参数为可变量,因此在黏性评估中亦采用无黏计算时的攻角,以保证可比性.从表中的计算结果可以看出,首先,在考虑前缘钝化及黏性效应条件下,乘波体的升力与无黏分析结果差别不大,但阻力明显增大.其次,乘波体的俯视投影面积不变,湿润面积差别较小,同时边缘钝化的形状也完全一致,因此较无黏结果而言,尽管阻力系数明显增大,但对所有构型而言,阻力系数的增量相对变化不大,均在0.05左右.
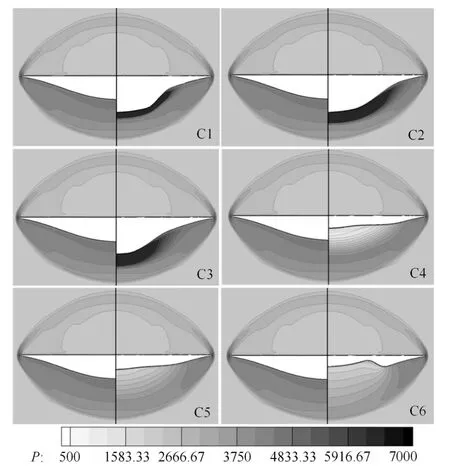
图12 不同乘波体尾缘压力分布云图比较Fig.12 Pressure contours comparison at trailing edge plane of dif f erent waveriders
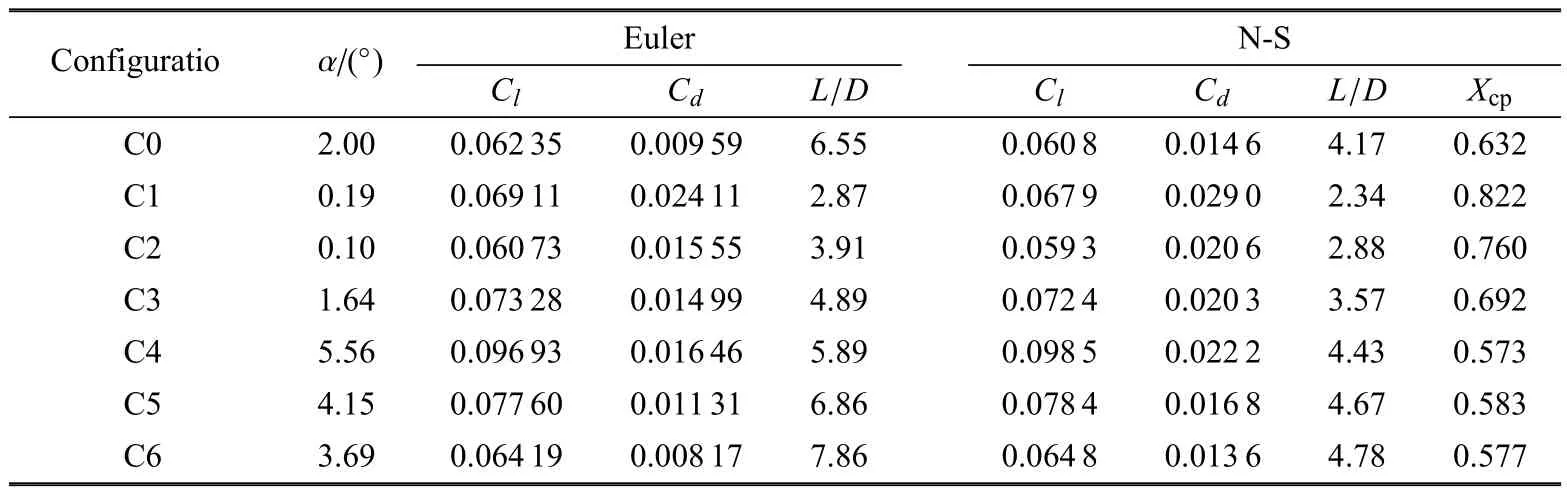
表3 典型构型黏性/无黏气动参数比较Table 3 Comparison of aerodynamic parameters based on dif f erent numerical models for typical waveriders
典型构型的选择是依据无黏升阻比递增原则,因此升阻比基本呈线性增加.考虑边缘钝化和黏性后,由于阻力增加,升阻比明显下降,但按构型顺序仍呈增加趋势.当乘波体厚度较小时,钝化边缘的脱体激波阻力及摩擦阻力所占总阻力的比重明显增加,因此无黏和有黏条件下升阻比差别明显增加,这一点在构型C5和C6的结果中体现尤为明显.由此可知,尽管考虑边缘钝化和黏性条件的升阻比极值与无黏条件下的升阻比极值不同,但在相当大的范围内,无黏和有黏升阻比变化规律相同.因此实际的优化设计中可以考虑先开展无黏优化,之后在无黏优化结果附近缩减所搜空间,再进行黏性优化或分析,可以有效减小计算量,提高计算效率.此外,在考虑钝化和黏性条件下,构型C1和C6的升阻比相差超过一倍.相对于初始C0构型而言,在升力不减条件下,升阻比也有超过14%的改善(构型C6).这表明通过压缩面的改变提升飞行器气动性能具有极大的优化空间.
图13给出了上述乘波体压缩面压力分布云图比较,从图中可见,随压缩面外形变化,物面压力分布差异明显,这是导致相应构型气动参数发生变化的原因.此外,压缩面压力分布的变化还导致俯仰力矩出现大幅变化,使构型的纵向压心产生偏移,如表3所示.
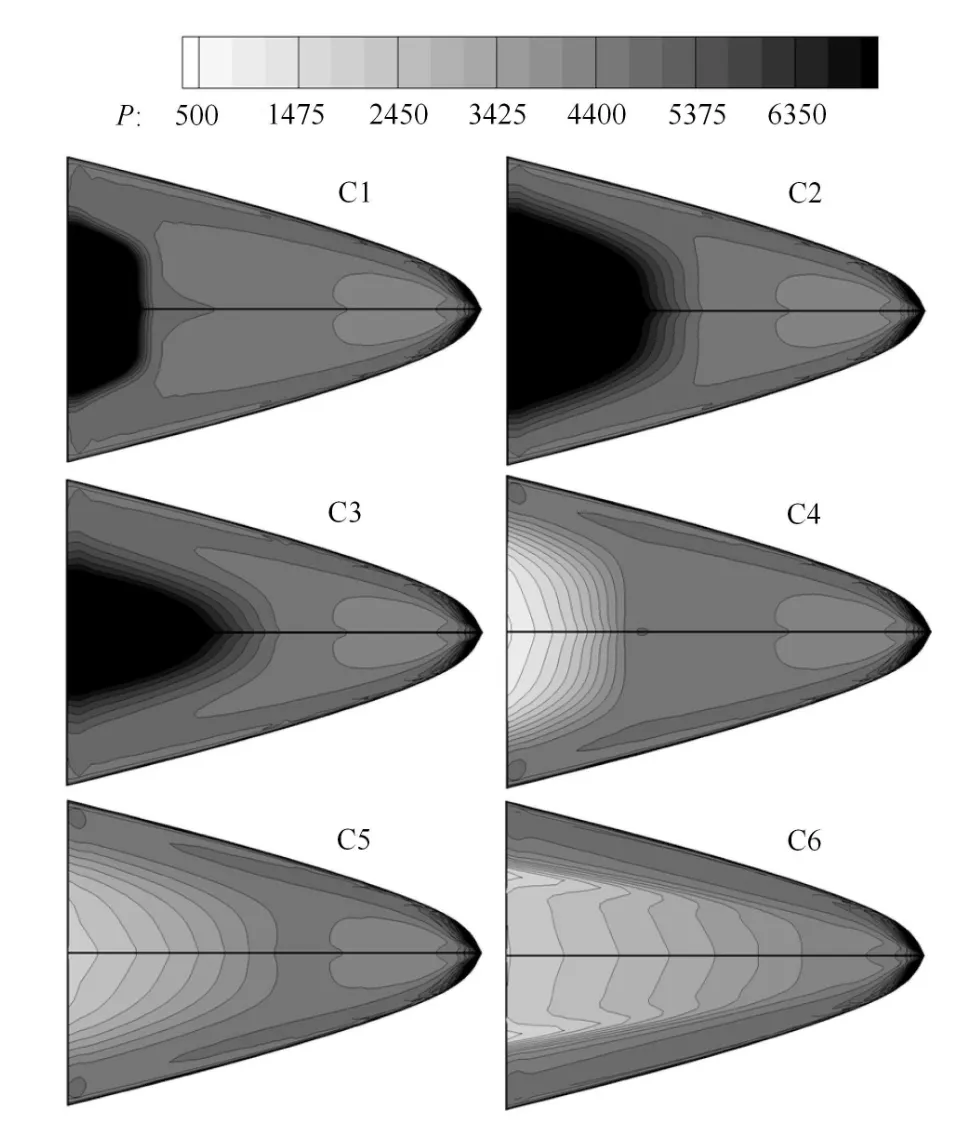
图13 不同压缩面乘波体压力分布比较Fig.13 Pressure contours on lower surfaces of waveriders with dif f erent compression surfaces
5 结论和讨论
本文给出了一种基于表面局部变形的乘波体设计方法,并在此基础上结合数值优化和计算流体力学方法评估了压缩面变化对乘波体气动特性的影响.结果表明,所给出的乘波体设计方法简便易行,与增量参数化方法相结合,可在较大范围内修改乘波体压缩面,且充分保持构型的乘波特性.数值优化结果表明,在前缘线(升力面积)不变的条件下,乘波体的升阻力系数及压心系数均具有较大的优化设计空间.在实际应用中,可结合实际需求,同时考虑升阻比、稳定性和配平特性等开展优化设计,应可取得明显效果.
对于本文所给出的乘波体设计方法而言,表面变形幅度和变形区域的选择对于构型能否保持乘波特性十分关键.增量参数化设计方法基于网格坐标系统改变外形,便于变形区域的界定,因此十分适合于压缩面优化.但目前的方法在变形区域的选择中主要依赖于经验,在后续工作中,基于空气动力学基本理论,在不同设计条件下对变形区域及变形最大幅度的合理选择开展研究,是一个十分值得探索的问题.
在本文工作中,乘波体的上表面采用自由来流面设计,并在优化和分析中保持不变.但从构型可以直观看出,此类乘波体的容积相对较小,通过优化,压缩面趋于平缓,随升阻比增加,容积减小更为明显.而在实际中,如果考虑容积需求,乘波体的上表面只能采用压缩面设计,这也将产生额外的阻力.此时应同时考虑上下表面形状变化开展优化,对于这类问题,本文的思路和方法可直接推广使用.此外,当在实际设计中考虑横航向稳定性时,采用本文的方法对乘波体压缩面形状进行修改和优化也将十分便利.
1 叶友达.近空间高速飞行器气动特性研究与布局设计优化.力学进展,2009,39(6):683-694(Ye Youda.Study on aerodynamic characteristic and design of optimization for high speed near space vehicles.Advances in Mechanics,2009,39(6):683-694(in Chinese))
2 Ferguson F,Dasque N,Dhanasar M,et al.Waverider design and analysis.AIAA Paper 2015-3508,2015
3 Lunan DA.Waverider,a revised chronology.AIAA Paper 2015-3529,2015
4 Ferguson F,Dasque N,Dhanasar M,et al.The design,analysis and performance evaluation of waverider configuration for hypersonic vehicle applications.AIAA Paper 2015-1008,2015
5 Jones JG,Moore KC,Pike J,et al.A method for designing lifting configuration for high supersonic speeds,using axisymmetric fl w fieldsIngenieur-Archiv,1968,37:56-72
6 Rasmussen ML.Waverider configuration derived from inclined circular and elliptic cones.Journal of Spacecraft and Rockets,1980,17(5):537-545
7 Doty RT,Rasmussen ML.Approximation for hypersonic fl w past an inclined cone.AIAA Journal,1973,11:1310-1315
8 Rasmussen ML,Clement LW.Cone-derived waveriders with longitudinal curvature.AIAA Paper 84-2100,1984
9 Takashima N,Lewis MJ.Waverider configuration based on nonaxisymmetric fl w field for engine-airframe integration,AIAA Pa-per 94-0380,1994
10 Cui K,Yang GW.Waverider configuration derived from general conical FlowfieldsActa Mechanica Sinica,2007,23(3):247-255
11 Cui K,Yang GW.The ef f ect of conical fl wfield on the performance of waveriders at mach 6.Chinese Science Bulletin,2007,52(1):51-64
12 Ding F,Liu J,Chen CB,et al.Novel approach for design of a waverider vehicle generated from axisymmetric supersonic fl ws past a pointed von Karman ogive.Aerospace Science and Technology,2015,42:297-308
13 吕侦军,王江峰,伍贻兆等.多级压缩锥导乘波体设计与分析.宇航学报,2015,36(5):518-523(LZhenjun,Wang Jiangfeng,Wu Yizhao,et al.Design and analysis of multistage compression conederived waverider configurationJournal of Astronautics,2015, 36(5):518-523(in Chinese))
14 Rodi PE.The osculating fl wfielmethod of waverider geometry generation.AIAA Paper 2005-0511,2005
15 贺旭照,倪鸿礼.密切内锥乘波体设计方法和性能分析.力学学报,2011,43(5):803-808(He Xuzhao,Ni Hongli.Osculating inward turning cone(OIC)wave rider-design methods and performace analysis.Chinese Journal of Theoretical and Applied Mechanics, 2011,43(5):803-808(in Chinese))
16 贺旭照,倪鸿礼.密切曲面锥乘波体--设计方法和性能分析.力学学报,2011,43(6):1077-1082(He Xuzhao,Ni Hongli.Osculating curved cone(occ)waverider:design methods and performance analysis.Chinese Journal of Theoretical and Applied Mechanics,2011, 43(6):1077-1082(in Chinese))
17 Lyu YC,Jiang CW,Gao ZX,et al.Passive waverider method and its validation.AIAA Paper 2014-4346,2014
18 Hu SY,Jiang CW,Gao ZX,et al.Design of periodic cruise vehicle based on the passive waverider method.AIAA Paper 2015-4546, 2015
19 Steelant J,Langener T,Matteo FD,et al.Conceptual design of the high-speed propelled experimental fligh test vehicle HEXAFLY. AIAA Paper 2015-3539,2015
20 Pezzella G,Marini M,Reimann B,et al.Aerodynamic design analysis of the HEXAFLY-INT hypersonic glider.AIAA Paper 2015-3644,2015
21 Ding F,Liu J,Shen CB,et al.Novel inlet-airframe integration methodology for hypersonic waverider vehicles.Acta Astronautica,2015,111:178-197
22 Liu J,Ding F,Huang W,et al.Novel approach for designing a hypersonic gliding-cruising dual waverider vehicle.Acta Astronautica, 2014,102:81-88
23 Li YQ,An P,Pan CJ,et al.Integration methodology for waveriderderived hypersonic inlet and vehicle forebody.AIAA Paper 2014-3229,2014
24 Cui K,Hu SC,Li GL,et al.Conceptual design and aerodynamic evaluation of hypersonic airplane with double flankinair inlets.Science China Technology Science,2013,56(8):1980-1988
25 胡守超,崔凯,李广利等.基于实验设计方法的高超声速飞机前缘型线优化分析.力学学报,2016,48(2):290-299(Hu Shouchao, Cui Kai,Li Guangli,et al.Optimization and analysis of the leading edge shape for hypersonic airplanes based on DOE methods.Chinese Journal of Theoretical and Applied Mechanics,2016,48(2):290-299(in Chinese))
26 Bowcutt KG,Anderson JD,Capriotti D.Viscous optimized hypersonic waveriders.AIAA Paper 87-0272,1987
27 Corda S,Anderson JD.Viscous optimized hypersonic waveriders designed from axisymmertirc fl w fieldsAIAA Paper 88-0396, 1988
28 张锋涛,崔凯,杨国伟等.基于神经网络技术的乘波体优化设计.力学学报,2009,41(3):418-424(Zhang Fengtao,Cui Kai,Yang Guowei,et al.Optimization design of waverider based on the artificia neural networks.Chinese Journal of Theoretical and Applied Mechanics,2009,41(3):418-424(in Chinese))
29 Lobbia MA,Suzuki K.Experimental investigation of a Mach 3.5 waverider designed using computational flui dynamics.AIAA Journal,2015,53(6):1590-1601
30 Ryan KM,Lewis MJ,Yu KH.Comparison of robust optimization methods applied to hypersonic vehicle design.Journal of Aircraft, 2015,52(5):1510-1523
31 Lobbia MA.Optimization of waverider-derived crew reentry vehicles using a rapid aerodynamics analysis approach.AIAA Paper 2015-0757,2015
32 Lobbia MA.Multidisciplinary design optimization of hypersonic transport configuration using waveriders.AIAA Paper 2014-2359, 2014
33 Bauer SXS.Analysis of Two Viscous Optimized Waveriders//Proceeding of the First International Hypersonic Waverider Symposium,1990,Univ.of Maryland,College Park,MD,USA
34 Charles EC.Interpretation of waverider performance data using computational fluidynamics.Journal of Aircraft,1994,31(5):1095-1100
35 Stron R,Price K.Dif f erential evolution—a simple and efficient heuristic for global optimization over continuous spaces.Journal of Global Optimization,1997,11:341-359
EFFECT OF COMPRESSION SURFACE DEFORMATION ON AERODYNAMIC PERFORMANCES OF WAVERIDERS1)
Cui Kai2)Xu Yingzhou Xiao Yao Li Guangli
(State Key Lab of High-Temperature Gas Dynamics,Institute of Mechanics,Chinese Academy of Sciences,Beijing100190,China)
(School of Engineering Science,University of Chinese Academy of Sciences,Beijing100049,China)
A waverider is a type of hypersonic lifting body that has the entire bow shock underneath the body as well as attached to the leading edge when flyin at its design Mach number.Present research for improving the aerodynamic performance of waveriders mainly focused on searching an optimal profil of the leading edge on the condition of given a specifi generatingfl wfield Inordertofurtherextendthedesignspaceofwaveriders,anoveldesignmethodthatisbased on a local shape deformation technique is presented in this paper.Moreover,an inviscid analysis-based optimization study was carried out to research the ef f ect of compression surface deformation on aerodynamic performances of waveriders by integrating the increment-based parameterization method,the computational flui dynamic analysis,and the dif f erential evolutionalgorithm.Afterwards,sixselectedwaveriderconfiguration werepolishedtobluntleadingedges,andthentheir aerodynamic performances were evaluated by solving the Navier-Stokes equations.The results show that both theL/Dand the relative pressure center coefficient of the waveriders produce significan changes with the variation of compressionsurface shape.Among all waveriders,the maximal dif f erence of theL/Dis more than double.Even by considering the lift constraint,the increment of theL/Dis more than 14 percent in comparison with the baseline configuration In addition, the value of relative migration of the relative pressure center coefficients is remarkable.
waverider,aerodynamic shape optimization,increment-based parameterization method,dif f erential evolution algorithm,computational flui dynamics
O354.4,V211.24
A doi:10.6052/0459-1879-16-041
2016-02-01收稿,2016-10-11录用,2016-10-13网络版发表.
1)国家自然科学基金资助项目(11372324,11572333).
2)崔凯,副研究员,主要研究方向:飞行器构型设计和优化.E-mail:kcui@imech.ac.cn
崔凯,徐应洲,肖尧,李广利.乘波体压缩面变化对其气动性能影响分析.力学学报,2017,49(1):75-83
Cui Kai,Xu Yingzhou,Xiao Yao,Li Guangli.E ff ect of compression surface deformation on aerodynamic performances of waveriders.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1):75-83

