基于优化LESA模型的高标准基本农田划定方法研究
——以重庆市合川区为例
程 杨,骆云中,王 帅,杨思思
(1.西南大学资源环境学院,重庆 400715;2.陕西省土地工程建设集团,陕西 西安 710075)
基于优化LESA模型的高标准基本农田划定方法研究
——以重庆市合川区为例
程 杨1,骆云中1,王 帅2,杨思思1
(1.西南大学资源环境学院,重庆 400715;2.陕西省土地工程建设集团,陕西 西安 710075)
为了摆脱层次分析法在LESA模型指标权重计算方法的不足,采用插值标度、建立调和函数的方法,对三标度法进行优化,计算矩阵权重向量和最大特征值,建立LESA指标权重排序模型,并划定重庆市合川城区周边基本农田为9 434.26 hm2。从模型来看,影响耕地质量的指标权重由大到小排列分别为气候条件、地形条件、土壤条件;影响立地条件的指标权重由大到小排列分别为区位条件、发展条件、利用强度。新方法包含传统层次分析法标度,摆脱了传统方法中元素对比阈值差异绝对值偏大的问题,在矩阵运算上的复杂性降低,且赏罚机制的触发在元素重要性对比中成功地控制了偏离平均值的元素值。该方法有较好的适应性,是优化LESA模型指标权重计算的有效方法。
调和函数;层次分析法;LESA;指标权重;合川区
LESA(Land Evaluation and Site Assessment)模型自1983年由美国土壤保持局提出以后[1],被广泛地运用到高标准基本农田划定[2-5]、农地效益评价[6-8]等领域。LESA指标的构建对模型的合理性起决定性的作用,而指标权重的确定很大程度上影响着LESA评价单元的最终值。当前,用于确定LESA模型指标权重的方法主要有:层次分析法、特尔斐法、灰色关联法、因子分析法,熵权法等,其中层次分析法运用最为普遍[9]。但是,在高标准基本农田和农地效益评价时,层次分析法涉及优劣势对比的指标较多,构建判断矩阵的运算复杂[10],且元素两两对比时无法控制两个对比元素的阈值范围[11]。因此,为了摆脱层次分析法在LESA模型指标权重计算方法的不足,笔者提出了基于调和函数的层次分析法,并运用该方法确定了合川基本农田划定的LESA模型指标权重,旨在简化层次分析法在LESA模型次级权重运算上的复杂程度以及提高LESA模型权重指标最终分值的准确程度。
1 研究对象
1.1 研究区概况
合川区地处重庆市北,地理坐标在东经105°58'37"~106°40'37"、北纬29°51'02"~30°22'24"之间,是渝西北、川东北的交通枢纽和重要的物资集散地,是重庆通往四川、陕西、甘肃等地的交通要道。截至2012年末,全区耕地面积120 801.54 hm2,占土地总面积的51.53%;其中,水田53 859.07 hm2、旱地66 940.59hm2,分别占耕地总面积的44.58%、55.41%。该案例涉及合川主城及其周边11个街道乡镇,涉及划定耕地面积18 385.89 hm2。
1.2 基础数据及评价单元划分
基础数据有图件数据、国民经济统计数据、检测数据、调查数据等。其中,图件数据包括土壤图、合川城区级周边地形图、DEM高程数据图、2010年土地利用变更调查数据、合川区耕地质量等级更新图、合川区城市周边基本农田划定举证数据以及重庆市土地利用总体规划数据(2012)等;国民经济统计数据包括2010~2012年合川区国民经济统计年鉴、合川区各个乡镇农林经济统计数据;检测数据包括土壤监测点检测数据、气象监测数据等;调查数据包括调查问卷数据等。评价单元以合川城区土地利用现状图为基础,利用Arcgis空间数据及属性特征叠加地形图、DEM高程数据、土壤图等划分10 150个评价单元。
2 研究方法
2.1 三标度法优化
三标度法是层次分析法的一种衍生方法,其优点在于:只有3个标度,有关专家很容易得出正确判断,减少了误差;容易构建最优传递矩阵,满足判断一致性。但是,三标度法自身也存在缺陷,例如:对指标的评价结果预期与实际情况偏离较远;没有能表示元素之间重要性差异的度量;无法控制两个对比元素阈值范围。以上缺陷的存在,使得三标度法在应用时有一定的局限性,通常用三标度法得到的评价结果与实际情况并不符合。因此,探索三标度法的合理优化方法尤为必要。
为了缩小两两元素重要性差异的阈值范围,只对两两对比元素重要性进行标度定义,而将两两对比元素原始标度之间的插值作为新的衡量标度,将标度扩充到五度,插值须符合以下原则:(1)赏罚调和原则,通过调和方程的建立,对明显优于或者明显劣于平均指标的元素进行调和运算,调和度通过调和斜率最大程度地体现出敏感性因素,调和的值与三标度法的计算值呈现差异,此差异体现对优劣于平均指标因素的赏罚;(2)科学合理原则,由于人们对指标因素概念的理解和认识不同,评分时具有一定的主观性和模糊性,所以在评分与定性分析的结果基本相符时,调和插值的标度应该建立在普遍认同的量值基础之上。
2.2 新标度的构建与确定
首先,根据赏罚调和原则和科学合理性原则构建新标度,对评价元素只做单项重要性比较(表1)。
其次,根据科学合理原则构建调和函数。通常,当i元素和j元素同等重要,定义标度为1;当i元素比j元素极其重要时,定义标度为5。于是提出形如X2k(其中k∈Q)的能满足合理性原则的调和函数来对原有标度进行转换,调和函数如下:

表1 插值标度

式中:Ti指调和标度,Tb指初始标度,k指调和系数。
调和系数k值决定了新标度之间阈值的大小。当k=1时,标度阈值变化小于原标度;当k>1时,阈值变化大于原标度;当k=0时,调和标度即为原始标度。所以在k取值时,需要根据评价对象的实际情况来确定。按照实际情况,k=1时,调和程度较为合适。通过调和函数,当Tb=2时,Ti=1.5,同理分别求得其他标度(表2)。
2.3 指标值的处理
首先,将指标按照公式(2)进行标准化处理,消除正向化或者负向化指标量纲,使指标在同一层次中具有可比性。

表2 构建的新标度

式中:v'指标准化后的指标值,vi指指标的初始取值,vmin指同维指标最小值(适用于负向化指标),vmax指同维指标最大值(适用于正向化指标)。
其次,同趋势化。指标的初始取值反映了各样本在某一方面的相互位置关系,因而在多指标综合评价时所有指标必须同趋势。

式中:v''指标准化、同趋势化处理后最终值。
2.4 指标的调和矩阵构建及权重计算
第一,分别对LESA模型中的次级指标和具体指标构建评价矩阵,然后根据公式(1)构建对应调和矩阵;第二,通过Mathematica工具集进行矩阵运算[12],求得调和矩阵的最大特征根,分别计算出次级指标和具体指标的权重向量;第三,然后通过公式 ,计算出CI的值。查询平均随机一致性指标RI值,检查是否符合一致性检验要求;第四,根据次级指标权重向量和具体指标层权重向量建立总排序模型。
3 结果与分析
3.1 指标体系建立
LESA模型的指标体系是双层结构体系,主级指标体系分别为耕地质量(LE)和立地条件(SA)。LE对应的次级体系Vx是体现土壤特征为主体的农用地自然属性的综合指标;SA对应的次级指标体系Wy是体现社会经济及区位对农用地利用方式的影响。为了全面综合反映评价对象,Vx、Wy应选择最科学的、最能反映系统特征的、最易度量的主导性指标。在此基础上,综合相关研究[6-7,13-14],根据研究对象和目的以及评价方法的需要,按照指标的全面性、灵敏性、科学性、可操作性[15-16]选取25个耕地质量次级指标和22个立地条件次级指标(表3)。

表3 主次级指标及指标内容
3.2 主级指标的权重比例确定
LESA的两个主级体系之间的权重比例根据不同地区的评价服务目标要求进行灵活的组合,美国在运用LESA模型进行耕地保护时,采用的比例组合为2∶1来确定LESA分值[13-14]。高标准基本农田建设的目标之一是粮食的高产稳产,自然质量与立地条件之间的权重比例关系都是为了粮食生产能力服务,因此两者之间的权重关系可以通过对粮食生产能力的影响来确定。研究以(0,1)区间,以0.1为标准间隔,对常量系数a、b逐一取值,测算不同权重关系下LESA体系的综合分值,最后用SPSS求出各样点综合分值与粮食标准粮产量的相关系数。经计算,相关系数最大为0.779,此时a=0.3,b=0.7,即为LE体系和SA 体系之间的最佳权重值比例为3:7(公式4)。
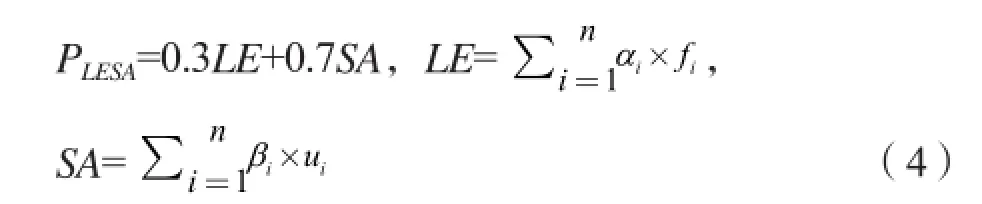
式中:PLESA为LESA评价分值;LE指耕地质量评价分值;SA指耕地立地条件评价分值;αi指耕地质量具体指标取值;fi指耕地质量具体指标对应的权重;βi指立地条件具体指标取值;ui指立地条件具体指标对应的权重。
3.3 次级指标的权重比例确定
(1)以立地条件SA次级指标为例,根据表2分别构建Wy及其具体指标内容W1的调和矩阵。
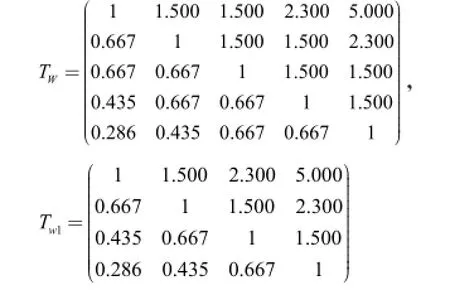
求得TW最大特征根λmax=5.121,及权重向量W=(W1,W2,W3,W4,W5)T=(0.377,0.301,0.114,0.183,0.139)T,Tw1最大特征根λmax=4.106,及权重向量w=(w1,w2,w3,w4)T=(0.495,0.211,0.187,0.107)T。
(3)查询平均随机一致性指标RI值可知,TW和Tw1对应5阶和4阶矩阵RI值分别为1.21和0.89。因此,根据CR=CI/RI求得TW和Tw1对应CR值,分别为0.027和0.034,皆小于0.10,符合一致性检验。
与此同理,构建耕地质量调和矩阵Tv、耕地质量次级指标V1~V7的调和矩阵和立地条件次级指标W2~W5的调和矩阵,分别求取λmax、权重向量以及进行一致性检验,如表4、表5所示。
3.4 总排序模型的构建结果与分析
根据主级指标权重和次级指标权重分类,分别构建耕地质量LE和立地条件SA的总模型。研究中耕地质量指标和立地条件主要有数值型指标、域值型指标和语言型指标3种类型[17];其中,α3~α5、α9、α18、α20~α22、α26~α27、α30属于数值型;α1~α2、α6~α8、α11、α13~α14等属于域值型;剩余属于语言型。根据《中国耕地质量等级调查与评定更新成果(重庆卷)》采用专家多轮评估赋值的方法确定其作用分值;β1~β3、β5属于数值型用缓冲分析赋予相应分值;β4、β6~β21属于域值型。根据统计年鉴、乡镇农林经济统计及其相关计算公式[5,18]进行因素分级赋值,最后进行标准化。(LE)αi和(SA)βi的取值分别与其对应的次级权重值相乘即可得到指标的最终分值结果,最后根据公式(4)将每个指标的最终分值结果与最佳权重系数相乘求和即可得到LESA评价分值(表6~表8)。

表4 次级指标调和矩阵及计算结果
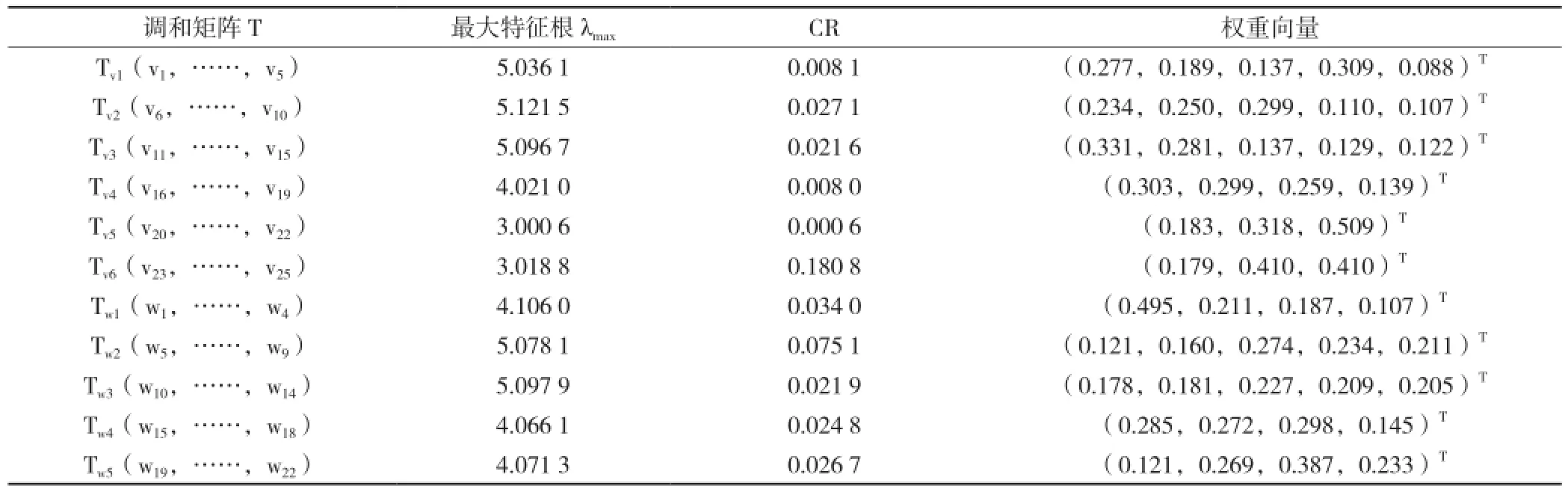
表5 指标调和矩阵及计算结果
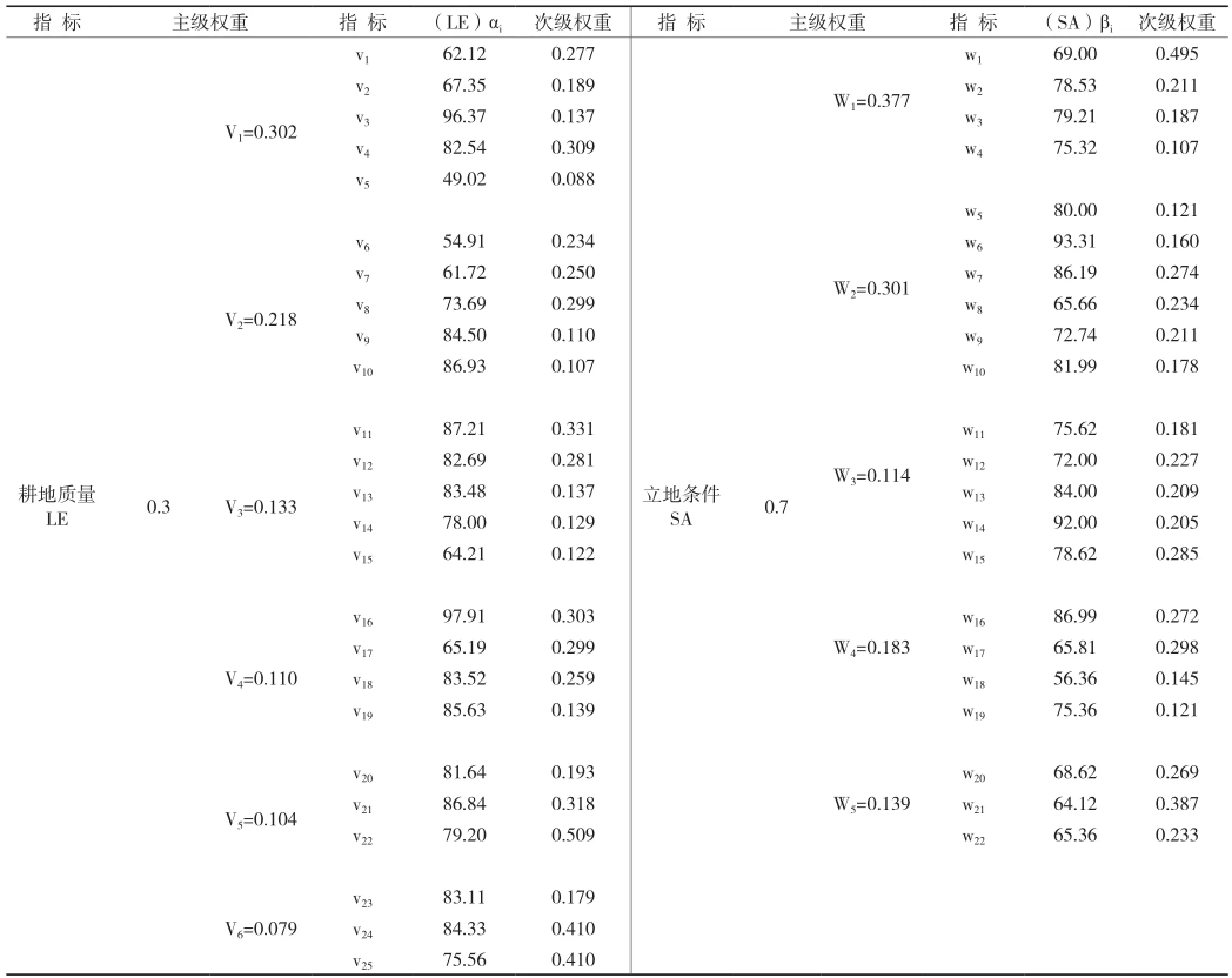
表6 合川区耕地质量与立地条件总模型

表7 合川区耕地质量和立地条件评价统计

表8 合川区耕地质量和立地条件综合评价统计
最后,对结果进行空间自然聚类,得到5级等分结果。由表8可知,合川城区周边基本农田LESA分值分布在19~89之间。采用等间距分类法,将其进行5类划分,如图1所示。其中,LESA分数>60的1、2、3级作为基本农田[5],基本农田面积为9 434.26 hm2。
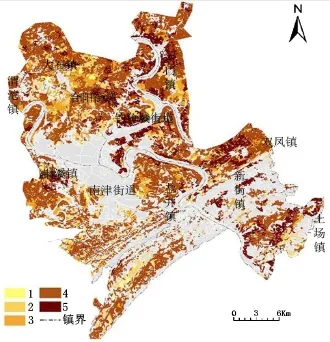
图1 合川区基本农田划定结果
4 结论与讨论
研究采用调和函数先对标度进行改进再用于排序权值计算,优化了LESA模型中需判别指标的权重,简化了矩阵运算,由于包含了传统的标度体系,改进后的方法适用范围更广、更全面。通过对重庆市合川区基本农田的划定实践,结果表明该方法控制了元素重要性对比的标度阈值,亦使得决策者易于构建判断矩阵,操作更简便,具有重要的现实意义。
对比改进方法前的相关研究[2,4,17]可以看出,在元素重要性的对比方面,改进的层次分析法通过调和系数k对初始标度进行调和运算,保证了出现敏感因素对比时对极敏感因素的调和,亦控制了极敏感因素重要性对比阈值的偏离,改进后的方法使得元素重要性对比的分值更加合理,更能突出模型中敏感性因素的权重地位;对比应用在LESA模型中的主成分分析法[18]、四象限法[19]、特尔斐法、因素成对比较法[20]等,改进的层次分析法在指标权重的确定上只有两层层次结构,操作更加简便,且在权重的计算上避免了复杂运算导致的指标信息进一步缺失的风险。需要注意的是,在对调和系数取值时,应该注意考虑优选对象的实际情况,对调和系数取值进行多名专家多轮评估,以保证调和系数取值的合理性和准确性。
[1] Richard W,Donford R,Dennis R,et al. Implementing LESA in Whitman County,Washington[J]. Journal of Soil and Water Conservation,1983,(2):87-89.
[2] 张 莹. 基于LESA模型的高标准基本农田建设潜力区划定研究一德化县为例[D]. 福州:福建师范大学,2015.
[3] 李晋龙. 基于LESA体系的延安市基本农田划定研究[D]. 西安:长安大学,2015.
[4] 张丹丹. 基于的黔江区金溪镇基本农田划定研究[D]. 重庆:西南大学,2013.
[5] 钱凤魁,王秋兵. 基于农用地分等和LESA方法的基本农田划定[J].水土保持研究,2011,(2):251-255.
[6] 张 帆,吴倩宇,邓楚雄. 主体功能区中基于LESA的农用地评价指标体系构建[J]. 湖南农业科学,2011,(5):48-50.
[7] 刘媛媛,胡月明,杨永忠,等. 基于LESA的佛山市农用地经济效益评价研究[J]. 广东农业科学,2013,(7):193-196.
[8] 张 依. 基于LESA体系的耕地质量综合评价及其应用研究[D].武汉:华中农业大学,2015.
[9] 屈 清. 基于GIS的永久性基本农田划定关键技术研究——以重庆市涪陵区为例[D]. 重庆:西南大学,2014.
[10] Jovana D,Milica V. AHP-based group decision making approach tosupplier selection of irrigation equipment[J]. Water Source,2014,41(6):782-791.
[11] Yasser M,Hossein B E,Zahra S A. Extension of fuzzy delphi AHP based on interval-valued fuzzy sets and its application in water resource rating problems[J]. Water Source Management,2016,30(9):3123-3141.
[12] 郑金銮. Mathematica辅助中学数学教学的实践、意义及其思考[D].福州:福建师范大学,2001.
[13] 涂建军,卢德彬. 基于GIS 与耕地质量组合评价模型划定基本农田整备区[J]. 农业工程学报,2012,(2):234-238.
[14] 刘瑞平,王洪波,全芳悦. 自然因素与社会经济因素对耕地质量贡献率研究[J]. 土壤通报,2005,(3):289-294.
[15] 代小平,陈 菁,陈 丹,等. 基于层次——集对分析方法的区域农业节水技术选择方法[J]. 灌溉排水学报,2013,(5):91-94.
[16] 江 红,程和琴,Francisco A S. 多准则渔业管理政策优选研究——以东海为例[J]. 资源科学,2010,(4):612-619.
[17] 刘琳琳. 基于LESA的城市边缘区永久基本农田划定研究——以沈阳市沈北新区为例[D]. 沈阳:沈阳农业大学,2016.
[18] 边振兴,杨子娇,钱凤魁,等. 基于LESA体系的高标准基本农田建设时序研究[J]. 自然资源学报,2016,(3):436-446.
[19] 唐秀美,潘瑜春,刘 玉,等. 基于四象限法的县域高标准基本农田建设布局与模式[J]. 农业工程学报,2014,(13):238-246.
[20] 沈 明,陈飞香,苏少青,等. 省级高标准基本农田建设重点区域划定方法研究——基于广东省的实证分析[J]. 中国土地科学,2012,(7):28-33.
(责任编辑:成 平)
High Standard Farmland Demarcation Method Based on Optimized LESA Model—Take Hechuan District of Chongqing as An Example
CHENG Yang1,LUO Yun-zhong1,WANG Shuai2,YANG Si-si1
(1. College of Resources and Environment, Southwest University, Chongqing 400715, PRC; 2. Shanxi Land Construction Group, Xi’an 710075, PRC)
In order to get rid of the problem of calculating the weight of LESA model index by analytic hierarchy process, the interpolation scale and harmonic functions were applied to optimize three-scale manner and calculate matrix weighting vectors as well as eigenvalue of maximum. LESA total ranking index weights model was established and the basic farmland around Hechuan was defined as 9 434.26 hm2. The weights of the indicators affecting the quality of the cultivated land were the climatic condition, the terrain condition, the soil condition. Weights of the indicators affecting the site conditions were location condition, development condition, utilization intensity. Conventional AHP was adapted to scale, which has solved the problem of lightly large absolute threshold differences. In addition, the complexities of matrix calculation were reduced. Furthermore, triggering the reward mechanism had successfully controlled element value of deviating from the average in the cooperation of elementary importance. The method of this article had properly great adaptation; meanwhile it was also an effective and feasible method to optimization of LESA model weight calculation.
harmonic functions; AHP-method; LESA; indicator weight; Hechuan District
S274;S277
:A
:1006-060X(2017)02-0062-05
10.16498/j.cnki.hnnykx.2017.002.017
2016-11-10
国家科技支撑计划课题(2015BAD06B04)
程 杨(1990-),男,重庆市人,硕士研究生,主要从事高标准基本农田建设研究。
骆云中

