导叶叶片数对轴流式油气混输泵内部非定常流场的影响

马希金，包春辉

(兰州理工大学，甘肃兰州 730050)

1 前言

在石油的开采过程中，多相混输技术不仅要实现油、气、水以及固体杂质的多相集输，而且还应具有液相泵和压缩机的双重性能。螺旋轴流式油气混输泵是多相混输技术发展的产物，是多相混输系统中的关键设备［1，2］。螺旋轴流式油气混输泵是由多个压缩级串联的多级泵，每一个压缩级都是由一个动叶和一个静叶组成，动叶叶片呈螺旋形，动叶、静叶均采用锥形流道［3］。螺旋轴流式油气混输泵的压缩级结构如图1所示。

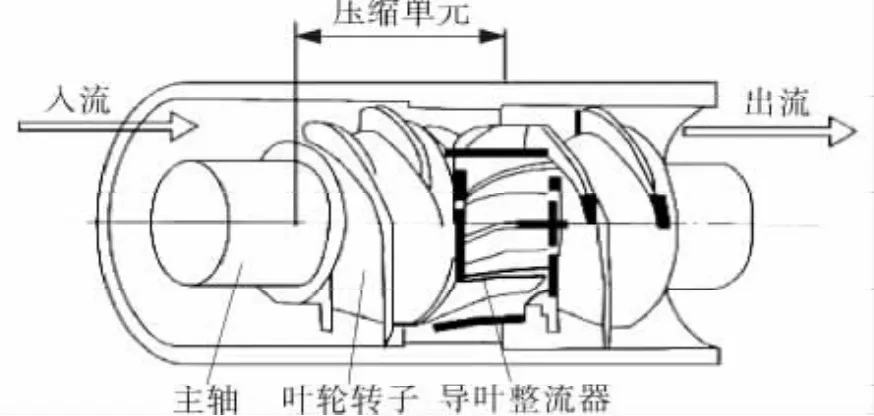
图1 轴流式油气混输泵的压缩级结构

本课题组对螺旋轴流式油气混输泵的研究已经逐步成熟，并对自主研发设计出的YQH-100型油气混输泵进行了优化。邵莲等通过改变叶片数优化叶轮，经过定常数值计算得出:叶片数为4时，动叶轮性能较佳［4］。文献［5］中研究了叶片数的变化对油气混输泵性能的影响，得出叶片数变化对混输泵效率的影响不大，适当增加叶片数可以降低叶轮比转速，提高扬程。李新凯等通过对本课题组研制的第三代油气混输泵导叶叶片数的研究发现，当导叶叶片数为13时，混输泵的效率和相对扬程均有所提高［6］。在文献［7］中对核主泵叶轮与导叶叶片数匹配规律进行了研究，阐明合理的叶轮和导叶叶片数对泵的水力性能的影响很大，在只改变导叶叶片数时，导叶叶片数的选取对核主泵效率影响的最大差值为8．48%。在轴流式油气混输泵中，导叶是连通上级叶轮与下级叶轮的中枢部件，导叶的性能直接影响着混输泵的整体性能，本课题组经过研发设计出了长短叶片交替的导叶叶轮。故在此基础上，本文将对导叶叶片数变化对混输泵性能的影响进行研究。

目前，对离心泵和斜流泵非定常的研究已较成熟，如文献［8］中阳君等对带导叶离心泵非定常流动时泵的特性曲线进行了分析，发现在小流量下泵内各种非定常流动会使泵的性能曲线出现驼峰或迟滞不稳定现象，文献［9］中张德胜等对斜流泵叶轮和导叶叶片数不同时压力脉动的变化进行了研究，得出在设计工况下导叶内部压力脉动波形主要受叶轮叶片数的影响。但对轴流式混输泵气液两相非定常的研究较少，文献［10］中余志毅等对叶片式混输泵气液两相非定常流动特性进行分析，发现高含气率时气相漩涡会造成气体局部聚集使混输泵的两相输运过程出现“不连续气团运动”的现象。所以本文就以YQH-100型油气混输泵为研究对象，基于气液两相流流动理论，利用FLUENT数值模拟软件对轴流式油气混输泵的导叶叶片数为7、8、9、10、11、13 时分别进行流场数值计算，并比较同一导叶叶片数下含气率为0．5和0时混输泵非定常流场的异同。

2 计算域模型网格划分

导叶叶片的设计选型在课题组之前的研究中已经很完善，本文中只是根据不同导叶叶片数的要求对模型进行适当的修改，来获得合适的计算域模型。本文使用ICEM-CFD软件选用非结构网格对建立的计算域模型进行网格的划分，计算域网格的网格单元总数为2676717，满足网格无关性假设。整机模型的计算网格如图2所示。

图2 轴流式油气混输泵计算域网格

3 数值计算方法

3． 1 控制方程

在油气混输泵流场的数值模拟中，一般将气相定义为空气，液相定义为水进行简化计算，并且采用Mixture模型作为两相流模型假，定气液两相的流型为泡状流，考虑到 Boussinesq涡粘性模型［11］。采用非定常不可压缩湍流流动的连续方程和动量方程作为控制方程。

连续方程:

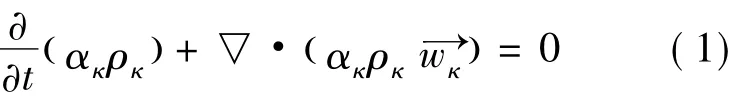
动量方程:

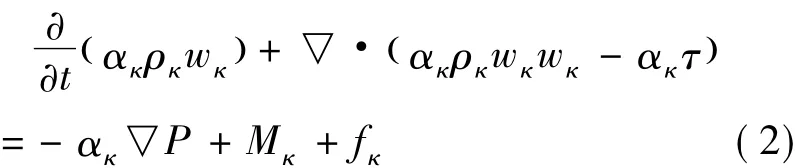
式中 ακ——κ相体积分数，满足αg+αl=1

κ——下标，任意一相(l为液相，g为气相)

ρκ—— κ 相密度

wκ——κ相相对速度

τ——粘性应力张量

P——压强

Mκ——κ相所受的相间作用力

fκ——与叶轮旋转有关的质量力，包括离心力和科氏力

湍流模型选用均相SST模型。这一模型在BSLκ-w模型基础上考虑了湍流剪切应力的输运，可对逆压梯度下的流动分离现象给出更精准的预测［12］。该模型下涡粘性系μt为:

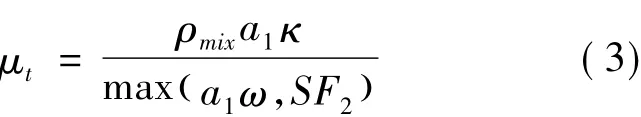
式中 ρmix——气液两相混合密度，即ρmix=αgρg+αlρl

a1——模型常数，a1=5/9

κ ——湍动能

ω——湍流频率

S——应变率的不变测度

F2——混合函数

3． 2 边界条件

在数值计算时，设定进口为速度进口，出口在不含气时为自由出流，含气率为0．5时为压力出口。将转动参考坐标系设在与叶轮一起旋转的流体区域上［13］，固壁面无滑移，由于叶轮是旋转的，而导叶是静止的，它们之间的交界面，引入滑移网格模型进行处理［14］。压力和速度的耦合方式采用SIMPLEC算法，离散格式均采用一阶迎风格式，收敛精度设为10－4。在混输泵非定常流动计算时，本文所选用的采样频率为5900 Hz，即非定常的计算时间步长为 Δt=0．0001695 s［15］，每 120个时间步长为1个叶轮旋转周期。在设计流量工况下，分别对6种不同导叶叶片数时的混输泵模型进行数值计算。为了得到混输泵内部的压力脉动特性，在靠近一级轴流叶轮出口处，二级轴流叶轮入口处，以及导叶内部共设置了12个压力脉动监测点，图3为监测点布置示意。图中点A1～A4和点C1～C4都在垂直于轴的断面上，并且4个点在同一半径上呈中心对称分布，而点B1～B4布置在导叶的单个流道内的流动方向上。

图3 监测点布置示意

4 计算结果及分析

4． 1 导叶叶片数对混输泵外特性的影响

从图4中可以看出，导叶叶片数n对扬程曲线的影响较大，其扬程的最大差值为7．9%，随着导叶叶片数的增加，混输泵的扬程逐渐下降，当导叶叶片数达到11后再增加叶片数时扬程保持平稳。导叶叶片数对效率曲线的影响明显，随着导叶叶片数的增加，含气率为0时，混输泵的效率先升高后降低，在叶片数为9时达到最优效率值;含气率为0．5时，混输泵的效率逐渐升高，其效率的最大差值为3．7%。这是由于随着导叶叶片数增加，导叶流道的内部空间被压缩，而加入气相后，泵内混合介质更容易受到挤压而改变气相的体积分数，导叶对混合介质的输运能力有所提升，从而使混输泵的效率得到了提高。

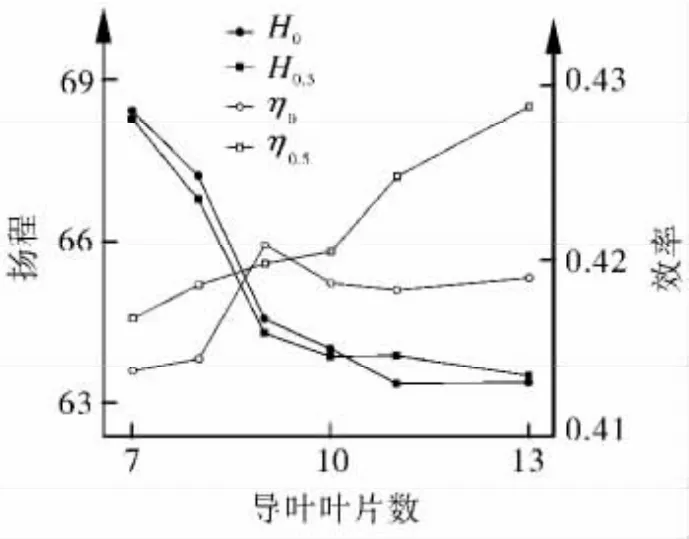
图4 导叶叶片数对混输泵外特性曲线的影响

4． 2 导叶叶片数对压力脉动的影响

通过数值计算可以得到混输泵内12个监测点上压力脉动的数据，可对不同导叶叶片数时的压力脉动进行分析，用压力系数反映压力脉动的程度，结果如图5～7所示。压力系数定义为［16～20］:

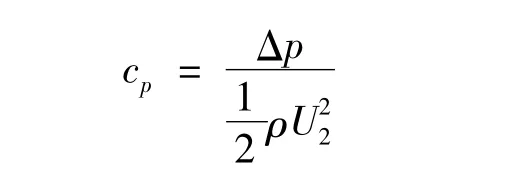
式中 Δp——监测点瞬态压力与叶轮旋转一周时均压力之差

ρ——流体密度

U2——叶轮外径圆周速度

图5 监测点A3压力脉动时域

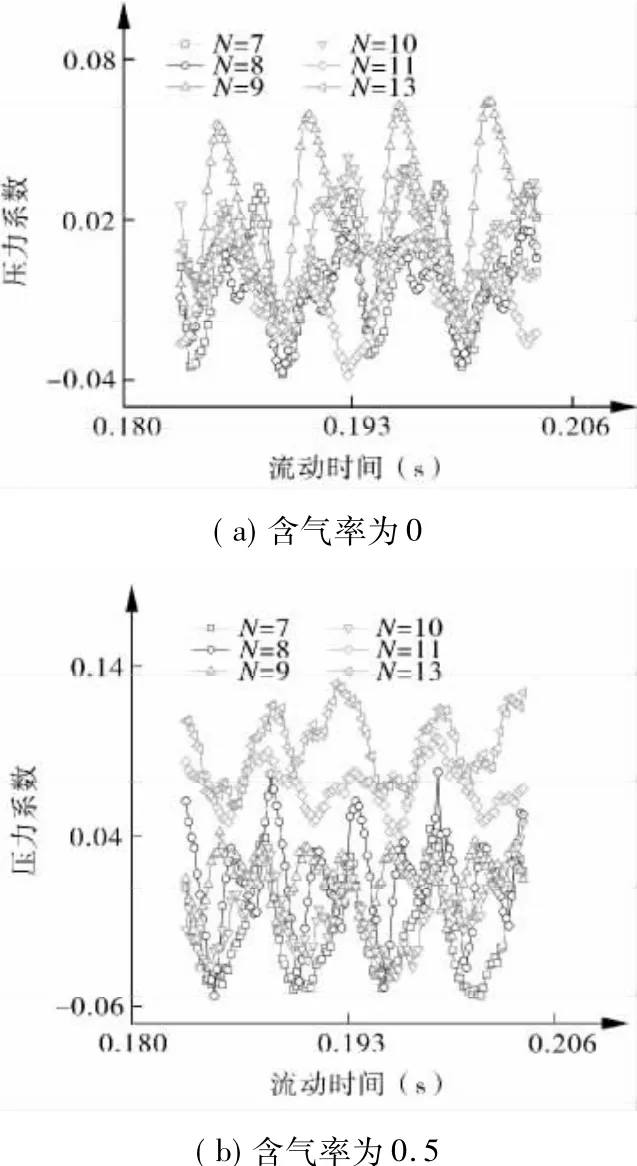
图6 监测点B3压力脉动时域

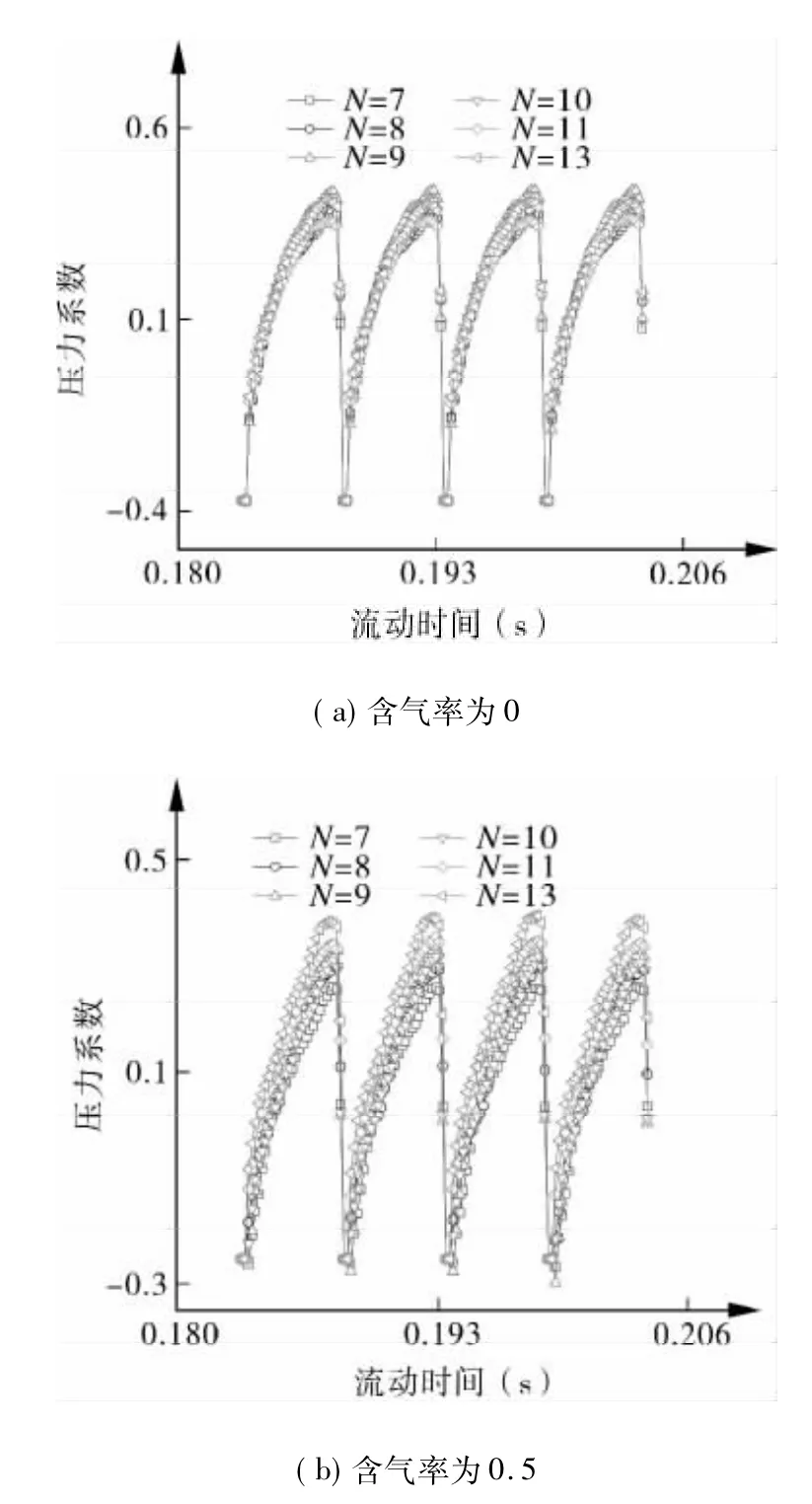
图7 监测点C3压力脉动时域

从图5可以看出，在一级叶轮出口处，压力脉动随导叶叶片数增加的变化不大，压力脉动的波形稳定，出现明显的4个波峰和4个波谷。从图6可以看出，在导叶流道中，压力脉动随导叶叶片数增加的变化很大，压力脉动的波形很不稳定，出现了二次波峰和波谷。从图7可以看出，在二级叶轮进口处，压力脉动随导叶叶片数增加的变化也不大，但压力脉动的幅值变化很大，压力脉动波衰减很快。比较图5～7可知，含气率为0．5时，不同导叶叶片数下压力脉动的变化更明显，随着导叶叶片数的增加，压力脉动的幅值越大。

由于导叶流道内压力脉动的变化较大，并且含气率为0．5时，导叶叶片数对压力脉动的影响更明显，故再对含气率为0．5时导叶流道内各检测点上的压力脉动进行分析。由于本文选用的采样频率为5900 Hz，其所对应的压力脉动的主频为195．032 Hz，非常接近叶片通过频率196．667 Hz，故在以下分析中将其简称为叶频。用傅里叶变换得到压力脉动的频域图，见图8。

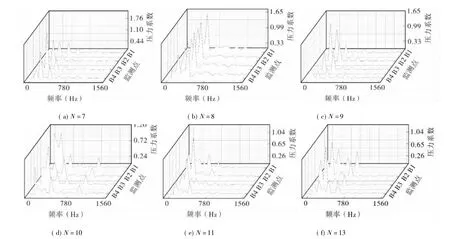
图8 导叶流道内压力脉动的频域

从图8中可以看出，导叶叶片数为7和9时，导叶流道内压力脉动以叶频的脉动特性为主，在导叶流道的中间位置压力脉动叶频的幅值较大，而在流道出口位置压力脉动明显减弱。导叶叶片数为8时，导叶流道内压力脉动以两倍叶频的脉动特性为主，导叶流道内沿流动方向压力脉动的衰减不明显。导叶叶片数为10，11和13时，导叶流道内压力脉动的波形较复杂，脉动频率还是以叶频为主。总体而言，随着导叶叶片数的增加，导叶流道内压力脉动的波形变得更复杂，压力脉动幅值的衰减变得缓慢，叶频压力脉动的幅值逐渐减小。

4． 3 导叶叶片数对叶轮内气相分布的影响

在多级油气混输泵中，随着叶轮级数的增加叶轮内压力增大，而叶轮内混合介质中气相占有的体积会缩小，气相的体积分数越少，混输泵的运行就越稳定，故本文对二级叶轮内部靠近叶轮轮毂处圆柱展开面上的气相分布进行分析，气相分布如图9所示。

图9 二级叶轮内气相分布

从图9中可以看出，不同导叶叶片数下，二级叶轮内气相分布不同。当导叶叶片数为7，8，10，11，12时，气体集聚现象十分明显，在二级叶轮内靠近轮毂处叶片出口边位置都出现了气体集聚的现象，在靠近叶片背面出口边处甚至出现了气团。只有当导叶叶片数N=9时，气相分布较均匀，气体体积分数也较低。所以导叶叶片数为9时，油气混输泵的运行更加平稳。

5 结论

基于SST模型，采用滑移网格技术，对设计流量工况下不同导叶叶片数轴流式油气混输泵的非定常流场进行数值计算，并在流场内布置压力脉动监测点，开展了导叶叶片数对混输泵的外特性、混输泵内部的压力脉动以及气相分布的影响。通过分析得出以下结论:

(1)导叶叶片数的变化对YQH-100型油气混输泵的扬程影响较大，对效率的影响较明显。随着导叶叶片数的增加，混输泵的扬程逐渐下降，其最大差值为7．9%;混输泵的效率在含气率为0和0．5时变化不同。随导叶叶片数增加，含气率为0时，混输泵的效率先升高后降低，当叶片数为9时达到最优值;含气率为0．5时，混输泵的效率逐渐增加，其效率最大差值为3．7%。

(2)含气率对混输泵内压力脉动的影响较大。含气率为0．5时，监测点压力脉动的幅值更大，压力脉动受导叶叶片数变化的影响也更明显。

(3)导叶流道内压力脉动受导叶叶片数变化的影响很明显。随着导叶叶片数的增加，导叶流道内压力脉动的波形变得更复杂，压力脉动幅值的衰减变缓，叶频压力脉动的幅值逐渐减小。

(4)不同导叶叶片数时，二级叶轮内的气相分布不同。当导叶叶片数为9时，气相分布较均匀，其他叶片数时，在靠近轮毂处叶片出口边位置出现了气体集聚的现象。

［1］ 冯志丹．含气率变化对轴流式油气混输泵轴扭应力的影响及改善［D］．兰州:兰州理工大学，2014．

［2］ 贾维斌．油气混输泵变工况条件下的密封性能分析［D］．兰州:兰州理工大学，2015．

［3］ 倪鹏博．动静叶轮轴向间距的变化对油气混输泵性能的影响［D］．兰州:兰州理工大学，2014．

［4］ 马希金，邵莲，曲鑫，等．油气混输泵叶片参数匹配的优化［J］．西华大学学报(自然科学版)，2009(2):74-76．

［5］ 马希金，赵杰，邵莲．叶片数变化对油气混输泵性能影响的研究［J］．流体机械，2009，37(6):24-27．

［6］ 马希金，李新凯，王楠，等．导叶叶片数对气液混输泵性能的影响［J］．兰州理工大学学报，2012，38(3):51-55．

［7］ 杨从新，齐亚楠，黎义斌，等．核主泵叶轮与导叶叶片数匹配规律的数值优化［J］．机械工程学报，2015，51(15):53-60．

［8］ 阳君．带导叶离心泵非定常流动对特性曲线驼峰的影响［D］．镇江:江苏大学，2014．

［9］ 张德胜，施卫东，王川．斜流泵叶轮和导叶叶片数对压力脉动的影响［J］．排灌机械工程学报，2012，30(2):167-170．

［10］余志毅，刘影．叶片式混输泵气液两相非定常流动特性分析［J］．农业机械学报，2013(5):66-69．

［11］ GRAY D D，GIORGIN A．The validity of the boussinesq approximation for liquids and gases［J］．Int J Heat Mass Transfer，1997，6(19):545-551．

［12］ MENTER F．Two-equation eddy-viscosity turbulence models for engineering application ［J］．AIAA Journal，1994，32(8):1598-1605．

［13］李新凯．气液混输泵优化设计及其数值模拟［D］．兰州:兰州理工大学，2012．

［14］ FERZIGER J，H PERIC M．Computational Methods for Fluid Dynamics［M］．3rd ed．Berlin:Springer-Verlag，2002．

［15］高强．导叶式混流泵压力脉动特性研究［D］．兰州:兰州理工大学，2014．

［16］马希金，张贞贞，侯祎华．多级油气混输泵轴向间隙变化对其性能的影响［J］．流体机械，2015，43(4):28-32．

［17］郭崇志，孙耀平，宋书伟．安全阀稳态与瞬态数值模拟技术对比研究［J］．压力容器，2015，32(2):27-34．

［18］王文博，刘厚林，王凯，等．1000 MW级核电站用喷淋泵泵壳安全性分析［J］．排灌机械工程学报，2015，33(5):402-406．

［19］杨敏官，邵腾，高波，等．熔盐泵分流式空间导叶内部流动及其非定常特性［J］．排灌机械工程学报，2015，33(4):306-310．

［20］ ZOBEIRI A，KUENY J L，FARHAT M，et al．Pumpturbine rotor-stator interactions in generating mode:pressure fluctuation in distributor channel［C］．Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems．Yokohama，Japan，2006．