基于H∞滤波的无序量测更新算法

赵凯，胡建旺，吉兵

（军械工程学院，石家庄050003）

基于H∞滤波的无序量测更新算法

赵凯，胡建旺，吉兵

（军械工程学院，石家庄050003）

在目标跟踪系统中，传感器量测因通信延迟无序地到达融合中心，产生无序量测融合问题。针对此问题，将H∞滤波作为基础滤波算法，提出了一种可处理单步或多步延迟无序量测的新算法。新算法借鉴有序滤波思想，利用等价量测来代替无序量测发生时刻后的量测序列，然后从该时刻起利用无序量测和等价量测进行有序更新。仿真实验表明，新算法相比于传统算法有更高的滤波精度，尤其在系统模型误差较大时仍有良好的滤波效果。

无序量测，H∞滤波，等价量测，有序滤波

0 引言

集中式目标跟踪系统中，各传感器的通信延迟、预处理时间与采样速率等存在差别，会有传感器信息不能同步到达融合中心的现象出现，这种现象称为异步现象［1-3］。在此情形下，对于同一个目标，若有较早时刻产生的量测在较晚产生的量测之后到达融合中心，则称这些量测为无序量测（Out-of-Sequence Measurement，OOSM）。

对于OOSM问题，Bar-Shalom等人提出了A1、 B1和C1等算法［5-7］，解决单步滞后OOSM问题。文献［6］提出了等效量测的概念，将A1算法的适用范围扩展到了多步滞后OOSM，并命名其为Al1算法。Thomopoulos算法［8］完全借助了信息滤波器，而后人们又在此基础上提出了更简洁有效、稳定性更强的OOSM滤波算法，如：AA1算法［11］，AAl算法［12］。上述算法都是以Kalman滤波为基础滤波算法，基于线性最小均方误差（Linear Minimum Mean Square Error，LMMSE）准则建立，因此，当系统建模误差较大，即系统模型不精确时，滤波效果下降严重。

H∞滤波通过极大极小准则，对过程噪声和量测噪声的统计特性作了最坏的假设，增强了稳定性和滤波精度。

对此，提出以H∞滤波为基础的新的OOSM更新算法。通过结合H∞滤波、有序滤波［10］与等价量测方法，算法可有效处理单步延迟和多步延迟无序量测问题，且在系统模型误差较大情形下有良好的效果。

1 OOSM问题描述

线性离散系统

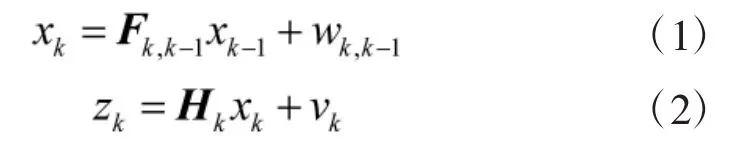
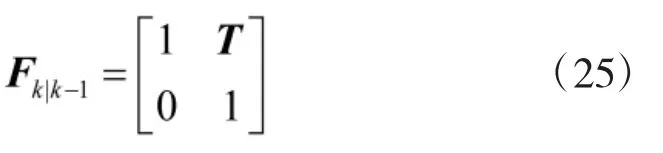
式中，Fk，k-1为时刻tk-1到tk的状态转移矩阵，Hk为tk时刻量测矩阵；wk，k-1为时刻tk-1到tk的累积过程噪声，vk是时刻tk的量测噪声，两者均为互不相关的高斯白噪声，方差分别为Qk与Rk。

假设tk时刻，已有状态估计

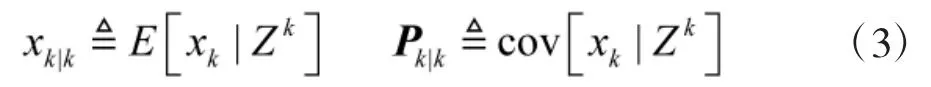
此时，需要用量测zd更新式（3）表示的tk时刻的状态估计，即计算

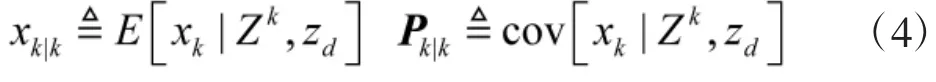
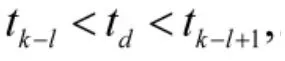
2 H∞滤波算法

Ravi Banavar在文献［13］中最先提出了基于博弈论的H∞滤波算法。H∞滤波算法采用极大极小准则，引入了H∞范数，在最大噪声作用下寻求干扰引起的误差范数最小，因而能够在系统模型不精确条件下，保证滤波精度，具有较强的稳定性。

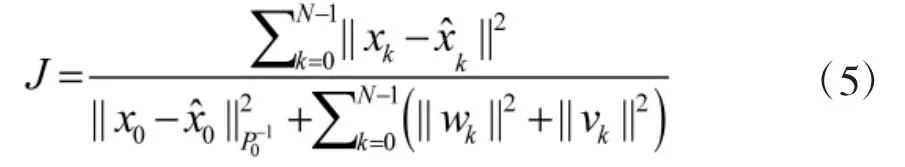
令

推导出H∞滤波方程［14］

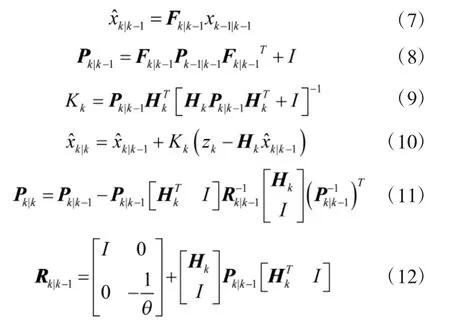
上述表明，参数θ取值对算法性能有重要作用：增大θ，可增强滤波器稳定性，但会降低估计精度；减小θ则与之相反。

3 基于滤波的无序量测更新算法

本文首次将H∞滤波算法应用到处理OOSM问题中。当融合中心收到OOSM后，将滤波过程返回至OOSM发生时刻，利用无序量测与等价量测按照H∞滤波方程进行有序更新。

3.1 等价量测方法

Bar-Shalom提出等价量测（EQM）方法［6］，将多步量测等价为单步进行处理。

由式（14）可知，等价量测

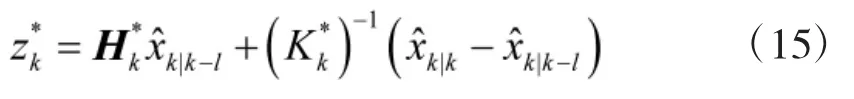
其中

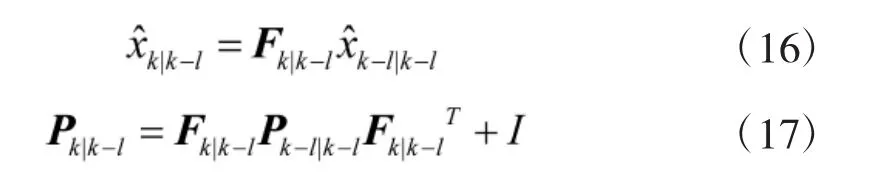
3.2 有序更新方法

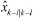
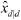
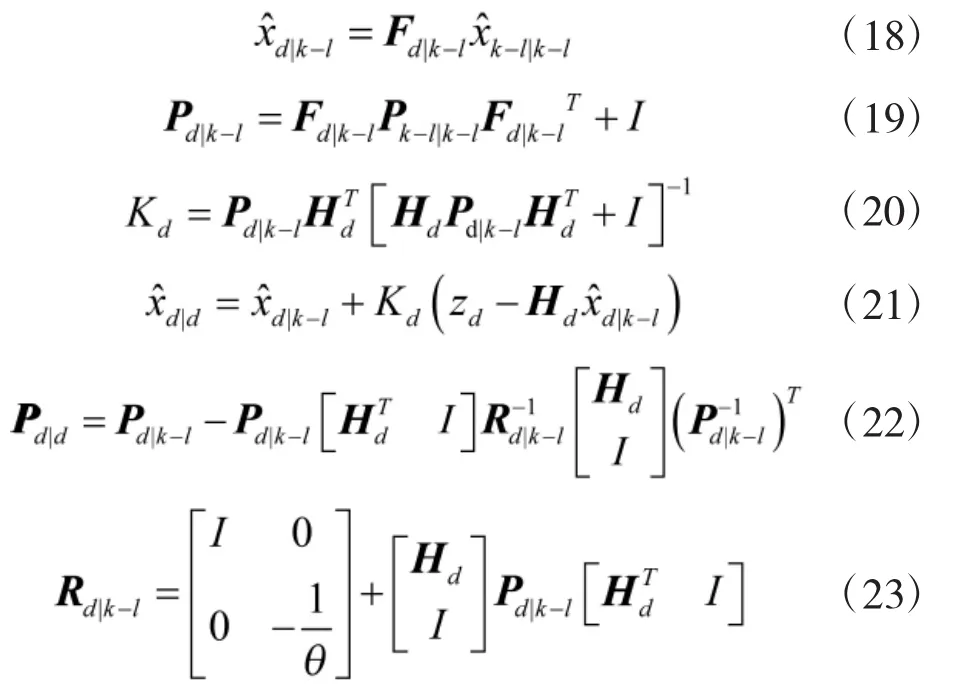
过程与第1步类似，不再赘述。其中状态转移矩阵

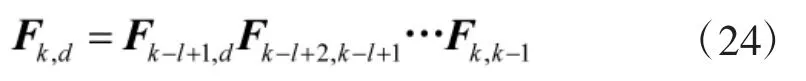
至此，完成整个OOSM更新过程。

4 仿真分析

假定目标沿轴做匀速运动，运动方程和量测方程式（1），式（2）。利用5个传感器对其进行跟踪。

式（1）中目标状态转移矩阵为

目标状态向量为

累积过程噪声协方差为

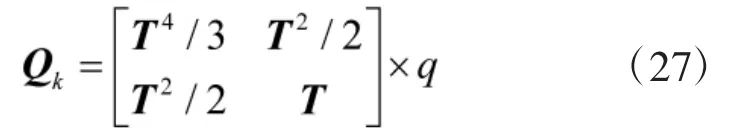
式（2）中目标量测矩阵为

量测噪声协方差为Rk=1。

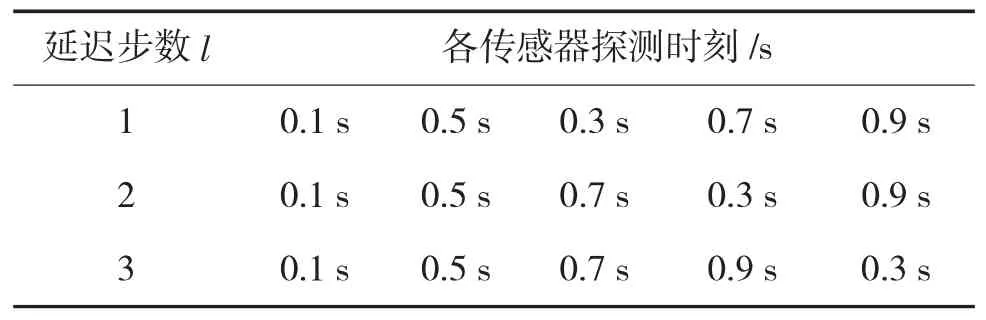
表1 TOOSM中各传感器观测时刻

为比较各算法处理无序量测问题性能，在仿真中选择滤波输出的位置分量均方根误差，其定义为

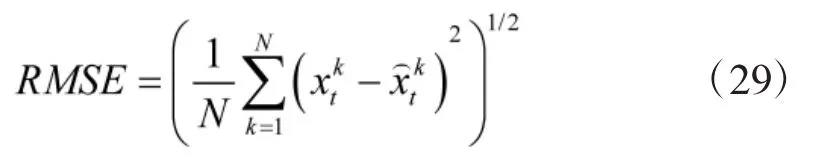
4.1 仿真1

如前文所述，θ的取值极大地影响新算法性能。假设延迟步数l=3，令θ分别取0.01、0.20、0.40、0.60、0.80、1.00、1.50，输出结果如表2所示。

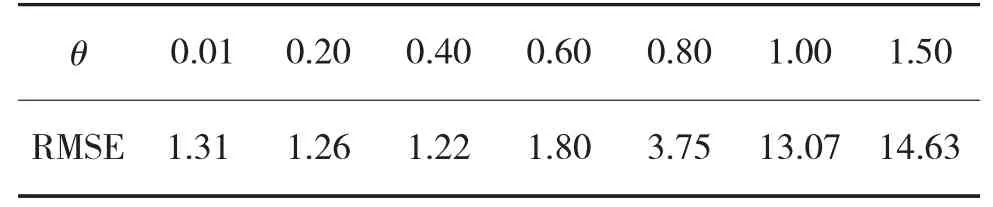
表2 不同θ时的位置分量均方根误差

以上取值中，θ=0.4时位置分量的均方根误差最小，因此，取θ=0.4。

4.2 仿真2

假设延迟步数l=1，3，使用新算法、Al1算法、AAl算法及数据缓存法分别进行处理，输出结果如表3所示。括号内数值为相对数据缓存法结果的偏差。

从表3可看到，以最优的数据缓存法为基准，新算法滤波精度远高于Al1算法，与AAl算法相似，并且随着延迟步数增加，性能下降不明显。

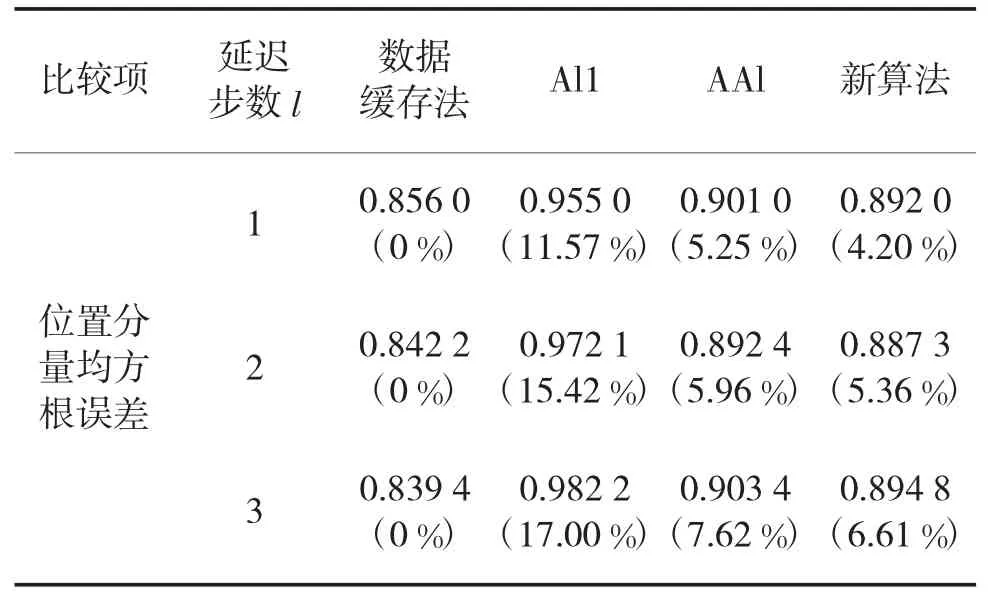
表3 仿真2中各算法结果比较

4.3 仿真3

假设每个融合周期内融合中心接收到传感器2的量测都是无序量测。对应于延迟步数l=1，3，分别使用新算法、Al1算法、AAl算法与数据缓存法进行处理，结果如下页图1所示。

从图1多个融合周期的滤波结果看，在单步延迟情形下，新算法滤波精度接近于数据缓存法，远高于Al1算法与AAl算法；但随着延迟步数的增加，其滤波精度稍有下降，但仍好于Al1算法与AAl算法。

4.4 仿真4

比较系统模型误差较大时各算法性能，验证滤波器稳定性。将状态转移矩阵设为

处理结果如图2所示。从图2看出，在系统模型有较大误差的情形下，新算法对单步延迟OOSM的处理有良好的效果，当延迟步数增加时精度下降，但仍远高于Al1算法与AAl算法。这是因为新算法基于H∞滤波，稳定性较好。

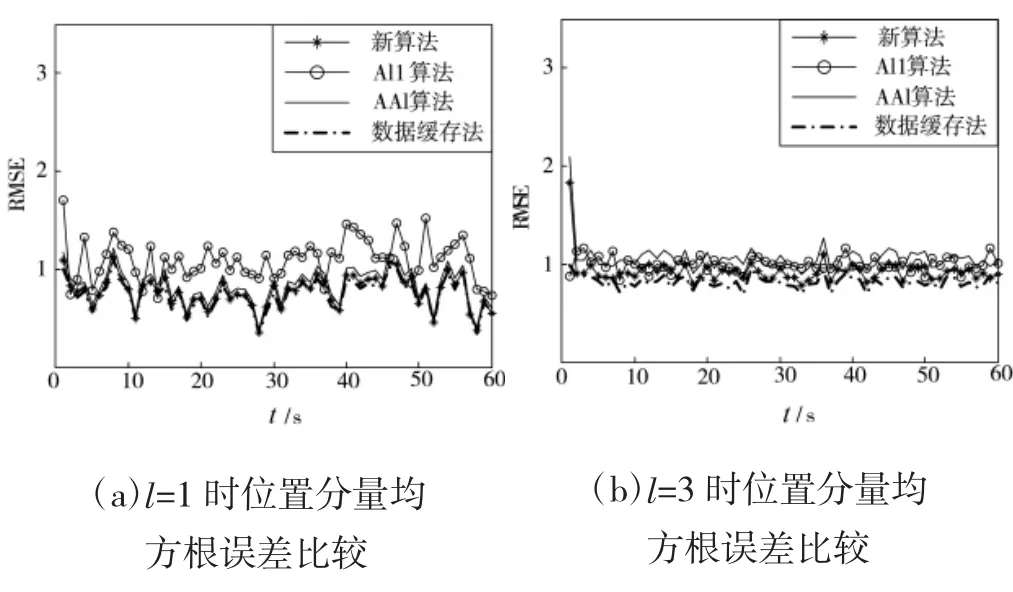
图1 仿真3中各算法结果比较

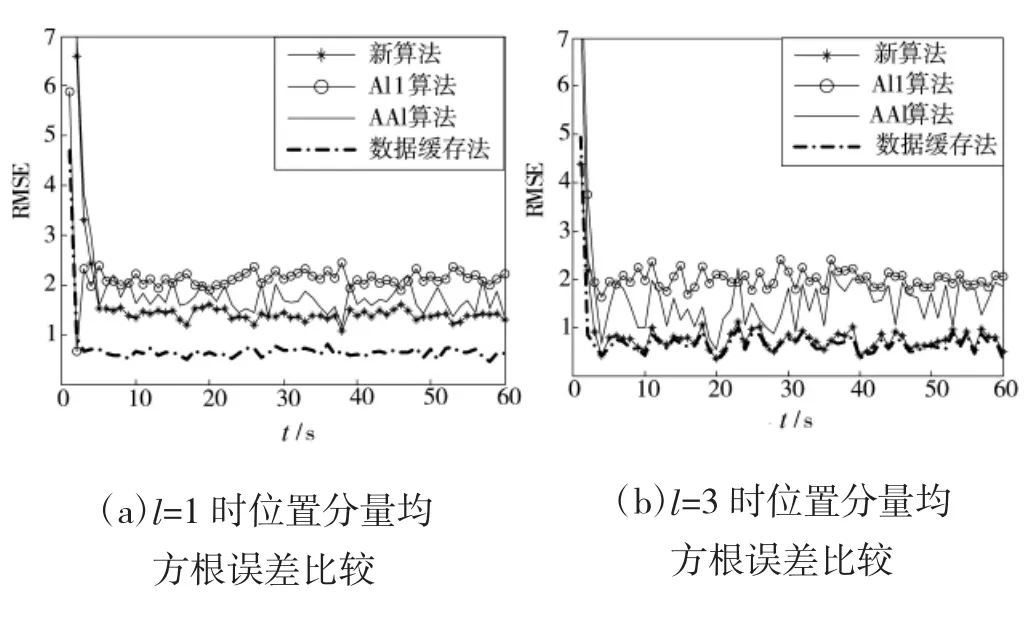
图2 仿真4中各算法结果比较

5 结论

新算法在有序滤波框架下，结合等价量测方法，使用H∞滤波算法对OOSM进行更新，可处理单步延迟与多步延迟OOSM问题，精度较高。仿真实验也验证了算法性能。今后，可以考虑将H∞滤波算法与粒子滤波等算法结合，解决非线性条件下无序量测问题。

［1］韩崇昭，朱红艳，段战胜，等.多源信息融合［M］.2版.北京：清华大学出版社，2010：368-379.

［2］王洪峰，周磊，单甘霖.国外军事信息融合理论与应用的研究进展［J］.电光与控制，2007，14（4）：13-17.

［3］王炜，黄心汉，王敏.无序量测滤波更新算法综述［J］.控制与决策，2012，27（1）：1-5.

［4］王炜，黄心汉，徐忠昌，等.一种新的无序量测处理算法［J］.电子与信息学报，2009，31（8）：1996-2000.

［5］BAR-SHALOM Y，MALLICK M，CHEN H，et al.One-step solution for the general out-of-sequence-measurement problem in tracking［C］//Aerospace Conference Proceedings，2002，IEEE，2002：4-1551-4-1559.

［6］BAR-SHALOM Y，MALLICK M，CHEN H，et al.One-step solution for the general out-of-sequence-measurement problem in tracking［C］//Aerospace Conference Proceedings，2002，IEEE，2002：4-1551-4-1559.

［7］BAR-SHALOM Y.Update with out-of-sequence measurements in tracking：exact solution［J］.Aerospace&Electronic Systems IEEE Transactions on，2002，38（3）：769-777.

［8］THOMOPOULOS S C A，ZHANG L.Decentralized filtering with random sampling and delay［J］.Information Sciences，1994（81）：117-131.

［9］ZHOU W H，LIN L I.Optimality analysis of one-step OOSM filtering algorithms in target tracking［J］.Science in China，2007，50（2）：170-187.

［10］黄细凤，吴钦章.顺序更新式无序量测处理算法［J］.传感技术学报，2012，25（2）：224-228.

［11］BANAVAR R N，BANAVAR R N.A game theoretic approach to linear dynamic estimation［J］.Thesis Texas Univ，1992（2）：42-45.

［12］SHEN X，SONG E，ZHU Y，et al.Globally optimal distributed kalman fusion with local out-of-sequence-measurement updates［J］.Automatic Control IEEE Transactions on，2009，54（8）：1928-1934.

［13］SHEN X，DENG L.Discrete H∞filter design with application to speech enhancement［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing，1995：1504-1507.

［14］侯代文.基于sigma点H∞滤波的说话人跟踪方法［J］.信号处理，2009，25（3）：374-378.

［15］ZHOU W H，LIN L I，GUOHAI C，et al.Optimal update with multistep out-of-sequence measurements in target tracking［C］//Proc of the 8th Int Conf on Signal Processing. Guilin，2006：281-284.

An Out-of-Sequence-Measurement Update Algorithm Based on H∞Filtering

ZHAO Kai，HU Jian-wang，JI Bing
（Ordnance Engineering College，Shijiazhuang 050003，China）

In target tracking systems，sensor measurements may arrive at the fusion center out of sequence because of the communication delays，which results in the Out-of-Sequence Measurement（OOSM）problem.Aiming at the above problem，taking H∞filtering as the basis filtering algorithm，a new algorithm can deal with both 1-step-lag OOSM and multi-step-lag OOSM is proposed.The new algorithm deal with OOSM by combing the framework of in-sequence filtering method the equivalent measurement is used to replace the measurement after the moment when the OOSM measured，and then updates from that moment with the OOSM and the equivalent measurement.Theoretical and simulations show that，compared to the traditional algorithm，the new algorithm has a higher filtering accuracy，especially when the system model error is large.

OOSM，H∞filtering，equivalent measurement，in-sequence filtering

TP391

A

1002-0640（2017）02-0159-04

2016-01-18

2016-03-16

赵凯（1991-），男，山东济南人，硕士研究生。研究方向：多源信息融合，目标跟踪。