基于T-S模型的非线性系统主从控制器设计*
蓝新波,赵志俊,杨善友,戴晨昱
(1.广东农工商职业技术学院,广州510507;2.广州大学,广州511370;3.中国移动通信集团广东有限公司,广州510623)
基于T-S模型的非线性系统主从控制器设计*
蓝新波1,赵志俊2,杨善友1,戴晨昱3
(1.广东农工商职业技术学院,广州510507;2.广州大学,广州511370;3.中国移动通信集团广东有限公司,广州510623)
针对同时具有输出和输入非线性的系统,通过中间虚拟控制量的设置,转化为两个非线性子系统的串联,从而简化系统结构并解决最终控制量不宜直接获取的问题。针对无人水面艇的航迹和横摇控制,设计了基于反演控制的从控制器,实现了输入非线性中虚拟控制量到舵角的映射,通过T-S模型将输出非线性系统,转化为线性时变系统,并考虑舵机的角度与角速度约束,设计了广义预测主控制器。该方法不仅简化了系统结构,同时仿真结果表明,所设计的主从控制器可以获得较好的控制效果。
输入输出非线性,T-S模型,广义预测控制,无人水面艇
0 引言
伴随着科学技术的发展和生产实践的不断深入,人类所面临的控制对象如航天器、机器人等越来越复杂,所要求的控制精度也越来越高。因此,复杂非线性系统的控制问题逐步成为控制领域的研究难点和重点。无人水面艇(Unmanned Surface Vehicle,USV)也是具有这样特点和控制要求的装置。USV具有灵活机动、低运行成本、无人员伤亡等特点,在反潜、反水雷、海上侦察与测量、港口警戒、护航、目标搜索与攻击等方面有着重要的用途[1-3]。伴随着通讯、导航和控制等技术的发展,USV迎来了一个高速发展时期,USV将和无人机一样在未来战争和民用方面发挥越来越重要的作用。
无论是反潜中声呐的布放、目标攻击中导弹或火炮的发射,还是海上测量中传感器的工作,都要求USV提供一个尽量稳定的平台。然而由于长度和吨位普遍较小,USV在工作中更易受到海浪、海风和海流等环境扰动的影响,使之发生大的摇荡。在USV六自由度的运动中,通常横摇阻尼最小,横摇角很大,影响其在高海况下的任务执行。同时由于USV的内部空间限制,除了必须的任务模块很难再放置单独的姿态稳定装置。
对于采用舵作为转向装置的常规排水型USV,由于舵的压力中心位于USV重心下方,同时横摇对舵的响应明显区别航向对舵的响应,因此,合理地控制舵角可以利用舵在保持航向的同时进行减摇操作。然而由于海况、浪向、航速和搭载任务模块的不同,使USV的运动方程具有很大的非线性和不确定性,对USV的运动控制提出了很大的挑战。USV的智能运动控制是一套非常复杂的系统,设计到自主航行与避碰等技术,作为其中的一个子项目,本文完成USV基本的航向与横摇控制。
针对USV等非线性系统,控制的主要方法有反馈线性化[4]、自适应控制[5]、变结构控制[3,6]和智能控制等控制方法[7]。这些方法都有其特定的应用范围,例如:常规的反馈线性化方法要求模型精确且全部状态可测,变结构控制中的抖振和智能控制中的实时性等问题限制了这些方法的应用。由于USV控制中非线性、不确定性、强干扰及需要考虑输入(舵角和角速度)和输出(航向偏差)约束等问题,使得如何设计一个具有满意性能的控制器变得比较困难。而广义预测控制中的滚动优化和反馈校正技术,能够对基于模型的预测进行修正,以适应变化的USV模型参数和海况,并且预测控制对输入和输出的约束处理比较直接[8]。因此,本文采用广义预测控制来完成USV的航向与横摇控制。
1 USV的运动模型
USV的运动模型可以采用不同的方式进行描述,如整体结构模型[9-10],分离型结构模型(MMG)[10-11]及响应型模型。忽略横摇和艏摇的耦合作用,可以把横摇与艏摇运动作为单独的两个方程来处理。由于工程技术人员对船舶的操纵性问题研究的比较深入,因此,直接反应舵角对航向影响的响应型模型获得了广泛应用。航向与舵角之间的关系可用下式表示[10]:
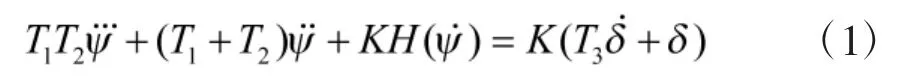
船舶的横摇运动方程可描述为:
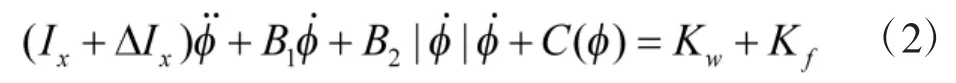

1.1 海浪扰动力矩
船舶在航行过程中不可避免地受到周围环境扰动的影响,其中最主要的是海浪的影响,海浪对船舶的航向保持和横摇稳定有着重要的不利影响。由于实际的海浪是随机的不规则波,很难精确进行计算,因此,可以采用波谱函数进行海浪波高的描述。采用ITTC双参数谱,其功率谱为:
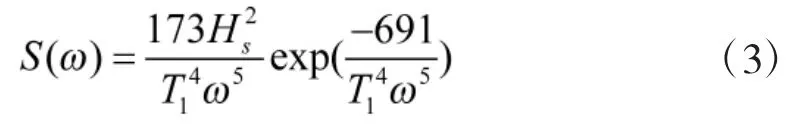
式中,Hs为有义波高,T1为平均过零周期。在仿真和控制系统设计中常采用成形滤波器法对海浪进行模拟,即用白噪声通过一个线性函数输出的谱密度与特定海况的谱密度近似。设成形滤波器的传递函数为:
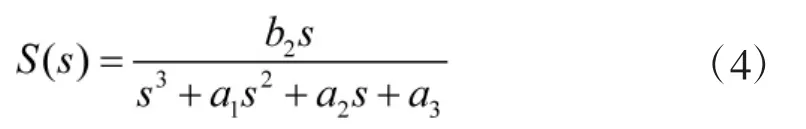
可以使白噪声经过式(4)之后的功率谱与式(3)接近来确定式(4)中的参数。
由于船舶的横摇运动对波倾更为敏感,而波倾的滤波器可描述为:

式中c为参数。
需要注意的是,海浪扰动分为高频的一阶扰动力距和低频的二阶扰动力距。一阶扰动力距是横摇的主要扰动,低频二阶扰动力距引起船舶航向改变和位置漂移。由于一阶扰动力距频率通常低于舵机伺服系统的工作频带,因此,可以用舵来实现减摇,但如果用舵机补偿一阶扰动引起的航向变化,会引起频繁的无效操舵而航向控制精度没有提升。
1.2 舵对横摇的控制力矩
考虑螺旋桨的影响,舵上的正压力可表示为:
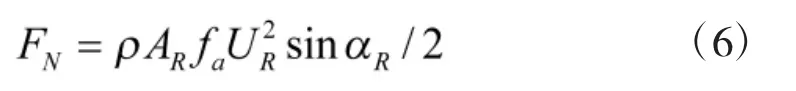
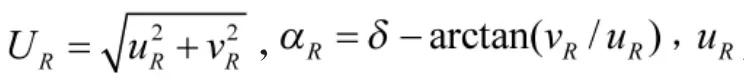

式中,zR为舵压力中心距USV重心的垂向距离,αH为考虑操舵诱导船体横向力之后舵力修正因子,zH为操舵诱导横向力中心至USV重心的垂向距离。
舵减摇控制器的输出为指令舵角,而舵机本身具有延迟和饱和等非线性限制,在控制器的设计时如果不考虑这些不利因素的影响,将导致控制性能变坏。因此,在进行控制器设计时,把舵机近似成为一阶惯性环节:

式中,δr为指令舵角,Tr为时间常数,并考虑舵角和舵角速率的影响。
1.3 运动模型的离散化
由于现在普遍应用数字处理器对被控对象进行控制,因此,需要对式(1),式(2)进行离散化:

式中,T为采样周期

忽略了横摇和艏摇的耦合作用,则系统控制式(9)分为航向控制子系统和横摇控制子系统。
2 控制器的设计
2.1 系统结构分解
由于系统的复杂性,为了降低设计难度,基于对舵减摇系统结构的分析,整个系统的设计可分为两步实现:①主控制器,根据航向控制计算舵角和横摇控制要求计算控制力矩(中间控制量)。②从控制器:根据式(6)计算所需舵角,并与主控制器计算的航向保持舵角进行合成,形成最终的控制舵角。
2.2 主控制器的设计
在主控制器的设计中,可以把航向和横摇控制作为一个整体方程进行设计,然而由于控制量与舵角δ有关,导致对约束的处理变得复杂。因此,可以把航向控制和横摇控制作为两个独立的子系统。由于航向保持是第一位的,首先根据舵角和角速度的约束计算指令舵角,第2步,根据航向保持获得的指令舵角、舵角和角速度的剩余容量、航速等信息计算约束条件,并据此计算。
由Takagi和Sugeno提出的T-S模型是一种比较典型的系统模糊模型,其在本质上是非线性的,但是构成模型的诸条规则均采用线性方程式作为结论部分。这样就使得T-S模型不仅能够在精度上逼近在紧集上定义的非线性函数,同时使得模型的输出具有线性的数学特性,可以采用成熟的线性控制方法来对非线性系统进行分析和控制[13-14]。
由于航向和横摇控制子系统设计过程相同,这里以横向子系统为例。对于式(9)中的USV非线性离散时间模型的航向控制,可以由m条模糊规则来表示,其中第i条模糊规则可表示为:[14-15]
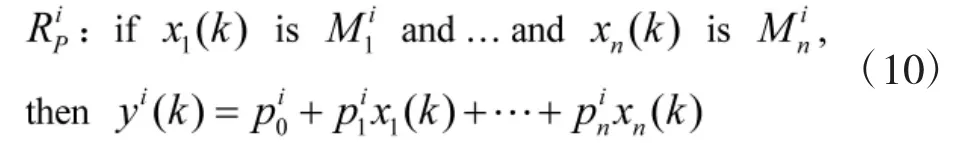
式中各参数的含义可以参考文献[16]。
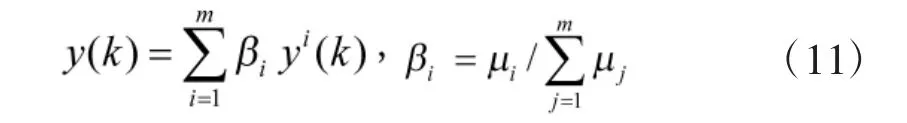
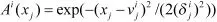
由于USV运动模型的时变和不确定性,对后件参数必须进行在线辨识来修正参数以保证USV模型的自适应性。同时,为了增加系统的实时性减小计算量,在每个采样周期并不需要对每个规则均进行辨识,而是计算规则的激励强度,只对具有最大激励强度的该条规则进行参数学习,并在递推最小二乘算法中加入遗忘因子:
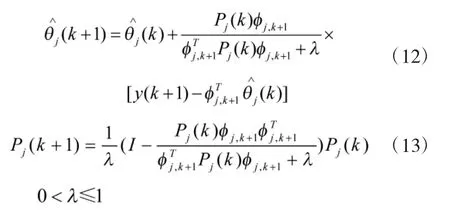
式中各参数的含义可以参考文献[17]。
采用带约束的输出预测误差和控制增量加权的二次型性能指标:
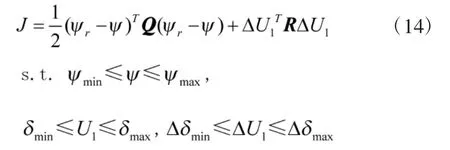
式中,ψr为参考航向,ψ为参考模型输出,ΔU为控制增量,Q和R为正定权重矩阵,分别为系统输出误差和控制增量的权值。目标函数的约束ψmax和ψmin、Δδmin和Δδmax、δmin和δmax分别为航向最大最小约束、舵角速度最大最小约束和舵角最大最小约束。
基于上述T-S模型航向控制子系统可以转化为下式的线性时变系统:
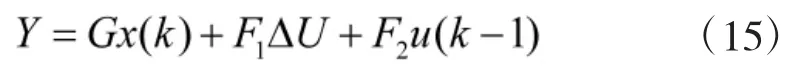
式(14)中的优化指标变为:
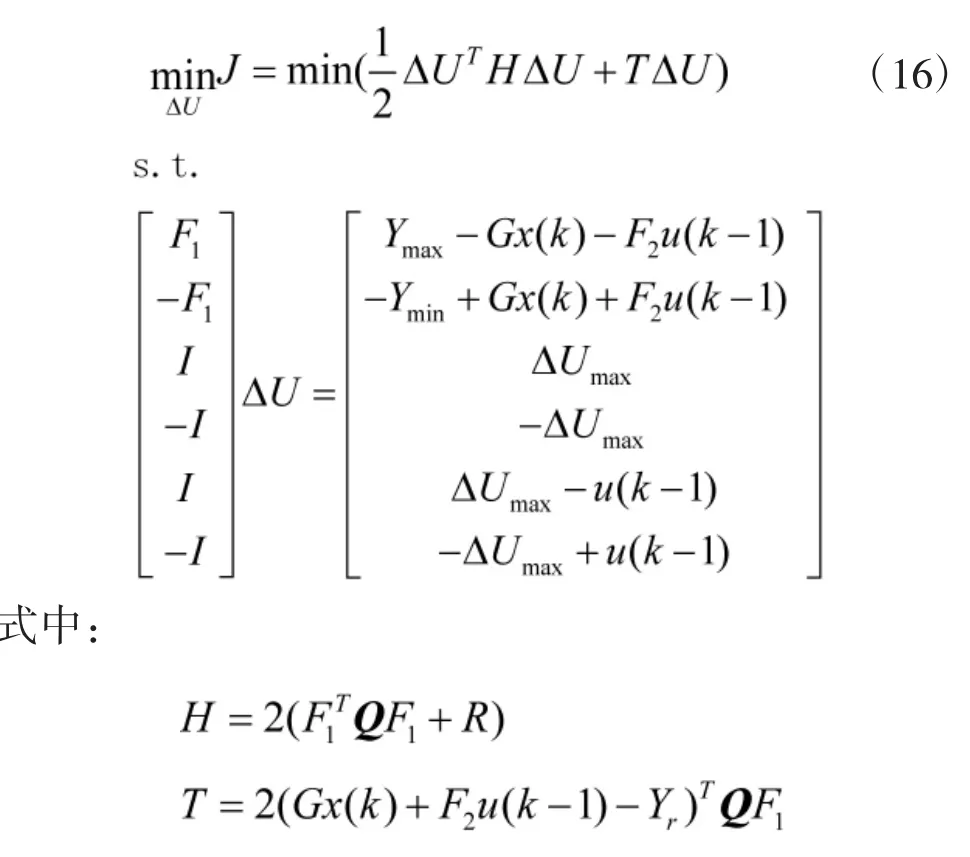

2.3 从控制器的设计
从控制器的目的是计算横摇稳定舵角δ2(k)使。为了解决Kf的非线性和结构的复杂性问题,采用数值迭代法进行从控制器的设计。由于控制器中采样间隔时间非常小,相邻采样点上和δ(2k)变化也将是很小量。因此,在计算当前时刻的控制量δ(2k)时,取前一采样时刻k-1时的计算值作为本次迭代计算的初值,采用Newton-Raphson迭代法使,则在从控制器中δ2(k)的计算中每一步的增量:
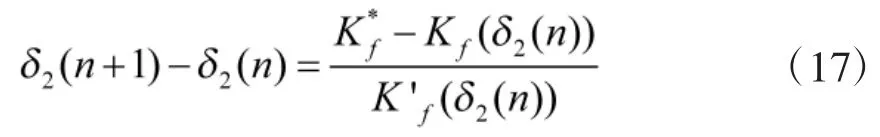
2.4 主从控制器框图
包含航向子系统和横摇子系统的主从控制器框图如图1所示。
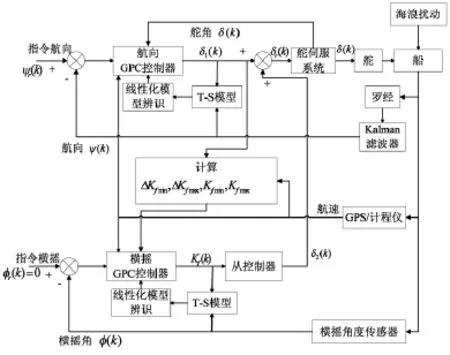
图1 控制器结构框图
由罗经获得的航向信号通常包含高频的一阶扰动,通常不希望用舵机补偿此一阶扰动引起的航向变化,以避免引起频繁的无效操舵,因此,需要对罗经获得的航向信号通过Kalman滤波器进行状态重构,只保留低频的二阶干扰,并且可以避免采用低通滤波器所引起的相位滞后。
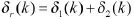
3 数值仿真
以某USV为例,其主要参数如下,总长Loa=9.0m,艇宽B=2.5 m,重心高度Zg=0.98 m,满载排水量Δ=5 000 kg。在有义波高Hs=2 m的条件下航行。
图2为使用舵减摇与未使用舵减摇时的横摇角对比,在未使用舵减摇时横摇角平均值为2.851 6°,使用后剩余横摇角为1.788 6°,减摇效果为37.3%。图3为使用舵减摇与未使用舵减摇时的航向角对比,在未使用舵减摇时航向角偏差的平均值为0.303 5,使用后为0.334 3,增加10.2%。使用后的航向偏差虽然有所增加,但航向偏差均在1度之内,可以满足USV的航向控制要求。
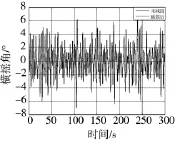
图2 横摇角
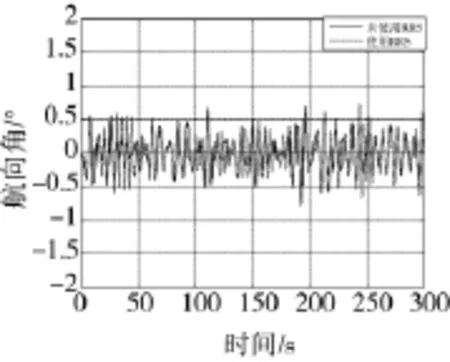
图3 航向角
4 结论
针对USV航行过程中的横摇控制问题,利用舵在保持航向的同时进行横摇减摇。针对USV航行过程中的非线性、不确定性和强干扰等特点,采用了基于T-S模型GPC控制器,并考虑了舵角的约束问题。所设计的控制器在航向控制满足要求的前提下,可以提供37.3%的横摇减摇效果。
需要注意的是,在使用舵减摇的同时,航向偏差增加明显,这主要是由于USV的吨位较小,船长较短,横摇周期和艏摇周期的频率相差较小。解决此问题的方法需要考虑图1中的指令合成方式,变直接相加为根据USV的姿态、当前舵角等来合成下一步的指令舵角。
[1]李家良.水面无人艇发展与应用[J].火力与指挥控制,2012,37(6):203-207.
[2]曹诗杰,曾凡明,陈于涛.无人水面艇航向航速协同控制方法[J].中国舰船研究,2015,10(6):74-80.
[3]廖煜雷.无人艇的非线性运动控制方法研究[D].哈尔滨:哈尔滨工程大学,2012.
[4]KWANGHEE N.Stabilization of feedback linearization systems using a radial basis function network[J].IEEE Trans. On Automatic Control,1999,32(10):1026-1031.
[5]CAI Z,QUEIROZ M S,DAWSON D M.Robust adaptive asymptotic tracking of nonlinear systems with additive disturbance[J].IEEE Trans.On Automatic Control,2006,51(3): 524-529.
[6]刘军,韩明文,俞金寿.基于滑模变结构的永磁同步直线电机控制系统研究[J].控制工程,2012,19(6): 1093-1096.
[7]李砚浓,李汀兰,姜艺,等.基于RBF神经网络自适应PID四旋翼飞行器控制[J].控制工程,2016,23(3): 378-382.
[8]CLARKE D W,MOHTADI C,TUFFS P S.Generalized predictive control[J].Automatica,1987,23(2):137-162.
[9]ABKOWITZ M A.Measurement of hydrodynamic characteristic from ship maneuvering trials by system identification[J]. Trans.of SNAME,1980,88:283-318.
[10]THOR I F.Handbook of marine craft hydrodynamics and motion control[M].Trondheim:WILEY,2012.
[11]YASUKAWA H,YOSHIMURA Y.Introduction of MMG standard method for ship maneuvering predictions[J].Journal of Marine Science&Technology,2014,20(1):37-52.
[12]BLANKE M,CHRISTENSEN A C.Rudder-roll damping autopilot robustness to sway-yaw-roll couplings[R].Aalborg:Aalborg University,1993.
[13]宋吉广,金鸿章,梁利华,等.全航速升力反馈减摇鳍控制策略研究[J].控制与决策,2011,26(9):1343-1352.
[14]王书斌,胡品慧,林立.基于T-S模糊模型的状态反馈预测控制[J].控制理论与应用,2007,24(5):819-824.
[15]苏成利,李平,邓淑贤,等.一种基于T-S模糊模型的自适应预测函数控制[J].控制工程,2007,14(6):610-613.
[16]苏佰丽,陈增强,袁著祉.多变量非线性系统的有约束模糊预测解耦控制[J].系统工程学报,2007,22(5): 546-550.
[17]刘忠信,孙青林,陈增强,等.基于T-S模型的钻杆对中自适应预测控制[J].控制与决策,2002,17(3): 372-384.
Design a Master-slave Controller for Nonlinear System Based on T-S Model
LAN Xin-bo1,ZHAO Zhi-jun2,YANG Shan-you1,DAI Chen-yu3
(1.Guangdong AIB Polytechnic,Guangzhou 510507,China;
2.Guangzhou University,Guangzhou 511370,China;
3.Chian Mobile GroupGuangdong Co.,Ltd,Guangzhou 510623,China)
To simplify system structure,a middle virtual control value is employed for both output and input nonlinear system,by which the system are separated to two subsystem and to get ultimately control value.A master-slave controller is designed based on the separated subsystem for trace and roll control of unmanned surface vehicle.The backstepping control is applied to map middle control value to rudder angle as slave controller.A T-S model is applied to change the output nonlinear system to linear time-varying system,and then the generalized predictive control with the constraints of rudder angle and angular velocity is introduced for the linear time-varying system as master controller.This approach not only simplifies the system structure,and simulation results show that the design of the master-slave controller can achieve good control effect.
Input and output nonlinearity,T-S model,generalized predictive control,unmanned surface vehicle
TP18
A
1002-0640(2017)02-0074-05
2015-11-07
2016-02-20
广东省教育厅优秀青年基金资助项目(YQ2015200)
蓝新波(1981-),男,广东河源人,副教授,硕士。研究方向:控制理论及应用、计算机网络。

