基于Smith法的高速巡逻艇极限强度评估

陈亮亮+简开勇+朱小楠+罗慧明+邓建通

摘 要：针对高速巡逻艇的极限强度评估问题，根据中国船级社《水面舰艇入级规范》（2011）的要求，给出了极限强度评估流程。以某新设计的高速巡逻艇为例，采用规范法计算了船体梁承受的极限弯矩，编写了校核在中垂和中拱工况下船体梁横剖面的极限弯矩能力的计算程序，根据程序计算结果对该艇进行了极限强度评估。结果表明，本文方法使用方便，精度满足工程要求，可为此类船型的极限强度计算提供参考。

关键词：高速巡逻艇；极限承载力；极限弯矩；Smith法；强度评估

中图分类号：U661.4 文献标识码：A

Abstract：This paper focuses on the ultimate strength of fast patrol boat and presents the whole evaluation procedure according to the requirement of the CCS Rules for Classification of Surface Naval Ship 2011.By taking a newly designed fast patrol boat as an example， the ultimate bend moment is calculated by the rule formula， and a code for calculation of ultimate capability under sagging and hogging conditions is developed， the codes calculation results are used to evaluate the hull girder ultimate strength of the boat. The result shows that this method operates conveniently with enough precision and can give reference for ultimate strength evaluation of the boat.

Keywords：Fast patrol boat； Ultimate capability； Ultimate bend moment； Smith method； Strength evaluation

1 前言

高速巡邏艇航速较快，结构重量较轻，在设计过程中会对其结构进行充分的优化。为了保证其结构安全，合理的评估其极限强度显得非常重要。准确计算其船体遭受的极限外载荷和评估其船体极限承载能力对高速巡逻艇的设计和营运具有重要意义。

本文首先基于CCS规范[1]给出的外载荷计算公式求得某高速巡逻艇的设计载荷，然后采用Smith法计算了船体极限承载力的计算流程，并根据规范要求进行了极限强度评估。

2 船型概述及计算流程

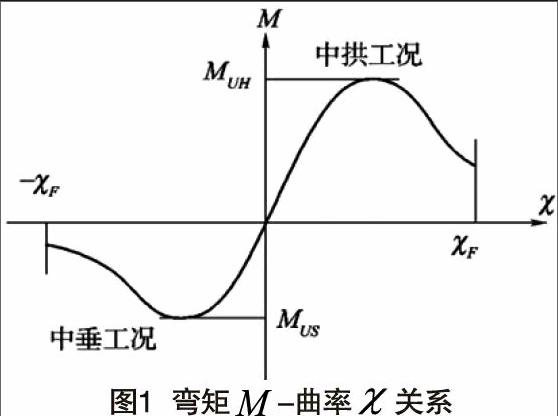
Smith法是计算船体极限弯矩的常用方法，其原理是增量-迭代法，也是目前CSR规范中推荐的计算方法[9]。通过逐渐增加船体纵向弯曲曲率的形式反映剖面构件的破坏过程，结合离散后的有效单元的力学性能分析，得到船体梁的弯矩-曲率曲线。当曲线的斜率减小至零时，所对应的弯矩即为船体梁的极限弯矩，如图1所示。Smith法考虑了构件的后屈曲特性，具有良好的精度，使用简单方便。

在计算中仅考虑船体梁垂向弯曲，忽略了剪力、扭转载荷、水平弯矩以及侧向压力的影响。

2.1 计算流程

船体梁总纵极限弯矩是船体梁的最大弯曲承受能力，超过此值船体结构将会被破坏。

（1）将船体梁横剖面离散成结构单元，即纵向加筋板格、硬角及横向加筋板格单元；

（2）导出所有单元的应力—应变曲线；

（3）导出期望的最大要求曲率。每一计算步的增量为。初始步的曲率增量，取为。根据船体梁横剖面的弹性剖面模数Zv-net50得到第一步计算的中和轴位置ZNA-1；

（4）对各单元（序数j），计算其对于曲率的应变、对应的应力及单元上的力；

（5） 通过检查剖面 上的总轴向力来确定新中和轴的位置ZNA-i，并调整ZNA-i的位置直到为止。

单元受压时为正，受拉时为负，重复步骤4 和5 直至达到平衡。当中和轴的变化小于0.000 1 m 时，即认为已达到平衡；

（6） 将各单元力的贡献相加，得到相应的弯矩：

（7） 按增加曲率，用当前中和轴位置作为下一步计算的初始值并重复步骤（4）到（6），直至达到最大要求曲率。

极限强度为M-k曲线的极值，若曲线的极值没有出现，则增加最终曲率Kf，至极值出现为止，计算流程见图2。

2.2 单元划分

（1）硬角单元：硬角单元是船体梁横剖面上刚度较大的构成单元，主要按弹性-塑性失效模式损坏，这些单元一般由两块不共面的板组成。硬角单元离板交点的范围是在横向加筋板上取20 tn50，在纵向加筋板上取0.5 s，见图3。

（2）普通扶强材单元：包括一个普通扶强材和带板。当扶强材两侧的板格是纵向加筋时，取带板宽度为普通扶强材的平均间距；当扶强材一侧的板格是纵向加筋，另一侧是横向加筋时，带板宽度取纵向加筋的宽度，见图3。

（3）加筋板单元：将包括纵桁或舷侧纵桁腹板的板格理想化为加筋板单元、普通扶强材单元的带板或硬角单元。

板格分为如下两类：纵向加筋板格，长边沿纵向；横向加筋板格，长边沿与纵向垂直的方向。普通扶强材单元之间、普通扶强材单元与硬角单元之间或硬角单元之间的板作为加筋板单元，见图3。表1给出了不同加筋板单元和普通扶强材单元的失效模式，不同失效模式对应的载荷-缩曲线参见[9]的附录2。

3 高速巡逻艇的船体梁极限载荷计算

中国船级社《水面舰艇入级规范》[1]中给出了作用在整个船体结构上的船体梁载荷，也给出了作用在船体局部结构上的用以校核结构局部强度的设计载荷。

由于舰艇航速不同，导致船体所受外载荷的性质也不同。根据表1的数据，本艇相对速度=10.21>7.38，属于高速船的范畴，因此，中拱计算弯矩和中垂计算弯矩按以下公式计算：

4 算例分析

4.1 船型概述

本文应用基于CCS规范[1]中给出的方法对某型高速巡逻艇进行船体梁结构的极限强度评估，该艇的有关参数见表2所示。

选取的船体校核位置如图5所示，应用Smith法将中剖面离散为67个单元。

分别计算弹性—塑性失效、梁柱屈曲、扭转屈曲、折边型材制成的扶强材腹板局部屈曲、扁钢制成的扶强材腹板局部屈曲和横向加筋板格的屈曲等不同失效形式下的各单元应力值，计算时调整中和轴高度ZNA-i高度，得到各单元上的应力，并使该剖面的和应力为零，从而输出剖面的和弯矩。然后递增曲率，再次调整中和轴高度，输出弯矩。最后绘制弯矩随曲率的变化关系曲线。

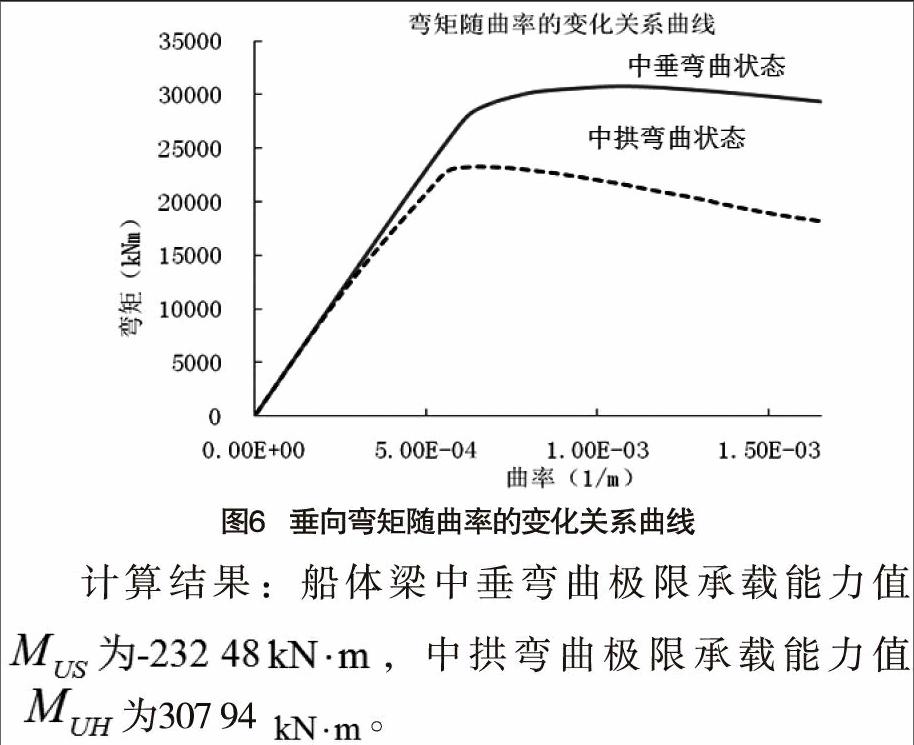
根据增量-迭代法，以曲率为横轴，垂向弯矩值为纵轴，绘制弯矩——曲率的曲线，如图6所示。

5 计算结果与分析

根据规范[1]的要求，在船体任一横剖面上的船体梁极限弯矩能力应满足下式：

6 结论与讨论

本文基于CCS《水面舰艇入级规范》（2011），对某新设计的高速巡逻艇的极限强度进行了计算。通过分析计算结果，可以得到以下结论：

（1）建立了高速巡逻艇的极限强度评估流程，根据评估要求可以采用规范公式计算船体所承受的极限弯矩；

（2）本文編写了基于增量-迭代原理的Smith法极限承载力计算程序。Smith法考虑了材料屈服、结构单元屈曲以及后屈曲的特性，很好地反映了船体剖面的实际破坏过程；

（3）本文建立的流程计算快捷，结果准确，可为今后类似的船体梁载荷和极限承载能力计算提供参考。

参考文献

[1]中国船级社.水面舰艇入级规范[S].人民交通出版社，2011.

[2]Vasta J. Lessons learnt from full-scale ship structural test. Trans. SNAME， 1958， 66.

[3]Caldwell J B. Ultimate longitudinal strength. Trans. RINA， 1965，107.

[4]Smith C S. Influence of local compressive failure on ultimate longitudinal strength of a ships hull[J] .PRADS， Japan， Tokyo. 1977，77.

[5]Yao Tetal. Analysis of the accident of the MV Nakhodka. Part 2.Estimation of structural strength. J Mar Sci Technol， 1998. 3.

[6]Soares， C. Luis， R.M. Nikolov， P. et al. Benchmark study on the use of simplified structural codes to predict the ultimate strength of a damaged ship hull. International Shipbuilding Progress， 2008，55.

[7]赵耕贤.船体与海洋工程结构设计技术[M].哈尔滨：哈尔滨工程大学出版社，2014.

[8]王雷，黄进浩，陈鹏，万正权.基于完整船体极限强度和搁浅剩余强度的协调共同结构规范对比分析[J].船舶力学，2015，19（4）.

[9]中国船级社.钢质海船入级规范[S].人民交通出版社，2015.