基于可变模糊决策理论的EPC项目总承包商的选择

张元节 曹建芮(华北水利水电大学 水利学院，河南 郑州 450045)

运行与管理

基于可变模糊决策理论的EPC项目总承包商的选择

张元节 曹建芮(华北水利水电大学 水利学院，河南 郑州 450045)

EPC总承包模式下，由总承包商来承担有关项目设计、采购和施工等风险。因此对业主而言，为确保顺利实施EPC项目，选择合适的总承包商尤为重要。在建立业主选择EPC总承包商指标体系的基础上，根据最小相对信息熵原理确定各指标的主客观组合权重，构建基于可变模糊决策理论的选择模型，利用其综合优属度的排序选择出可靠的总承包商。以采用EPC模式的W水利工程为例，进行总承包商的评价和决策，结果表明该选择方法合理可行，具有一定的借鉴意义。

EPC模式；总承包商选择；可变模糊决策理论；组合权重

近年来，一种采用固定总价合同的新型承包模式，即“设计—采购—施工”(EPC)总承包模式在水利工程中逐渐得到推广。根据我国水利工程项目的特点及国内外EPC总承包模式的实践经验可知：EPC总承包模式主要适用于具有庞大投资规模、较长设计和采购周期的水利工程项目[1]，同时也要求总承包企业具有复杂的专业技术及较高的管理水平。因此，如果业主没有选择合适的总承包商，将会给其带来意想不到的经济损失。

目前，对选择EPC总承包商的研究主要从指标体系和选择方法两个方面进行。王显鹏等人构建了对若干个候选总承包商的综合能力进行排序的选择模型[2]；杨晓辉在其硕士论文中对于业主在不同阶段选择总承包商时应考虑的影响因素进行了详细研究[3]；孟宪海、赵启对业主选择EPC项目总承包商时的相关标准及应遵循的原则进行了阐述[4]。但是，已有的研究大多仅考虑了主观因素的单一选择模型，结果具有一定的主观性。

在现有研究成果及可变模糊决策理论的基础上，建立了EPC总承包商选择的模型，综合了模糊综合评价模型、神经网络系统中的非线性模型、理想点模型和模糊优选模型等4种模型的评价结果，且采用由层次分析法(AHP)和信息熵确定的主客观组合权重，弥补了现有选择模型所得结果的偶然性和主观性，为业主选择EPC项目总承包商提供了一种新的思路和方法。

1 构建选择总承包商的指标体系

在实际选择EPC总承包商时，业主并非完全考虑到很多影响因素。为了使其客观选出合适的承包商，综合相关文献及专家意见，遵循指标体系的建立及选择总承包商的原则，在相关标准的指导下，借鉴类似工程经验，经本专业若干专家及业主单位负责人商讨后，对文献[2]中影响业主选择EPC项目总承包商的相关因素作进一步细分。最终构建一个由5个一级指标和16个二级指标(其中5个为定性指标，其余的为定量指标)组成的递阶层次分明的指标体系，具体如图1所示。

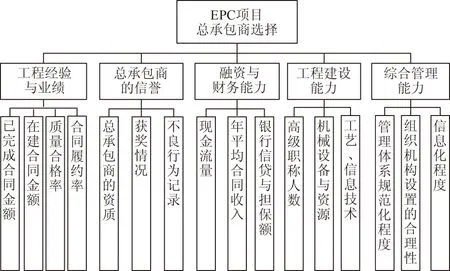
图1 业主选择EPC总承包商的指标体系

2 建立总承包商选择模型

2.1 可变模糊决策模型[5]

在文献[5]中，陈守煜建立了两级可变决策模型，具体为

(1)

式中,i为可供业主选择的总承包商的个数(i=1,2,…n)；ui为总承包商i的综合相对优属度；dgi为决策的距优距离;dbi为决策的距劣距离；α为优化准则参数(α=1,2 ，分别为最小一乘方和最小二乘方准则)。

(2)

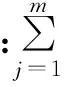
(3)

通常情况下，根据α和p的取值(α=1,2;p=1,2)，其组合方式主要有以下4种:α=1,p=1;α=1,p=2;α=2,,p=1;α=2,p=2。

(1) 当α=1,p=1时

则

(4)

此时为一个相当于模糊综合评价模型的线性模型。

(2) 当α=1,p=2时

则

(5)

在dgi和dbi的表达式中取p=2，此时相当于理想点模型。

(3) 当α=2,p=1时

则

(6)

此时为可用于描述神经网络系统中神经元的非线性特性或激励函数的sigmoid型函数。

(4) 当α=2,p=2时

则

(7)

且在dgi和dbi的表达式中取p=2，此时相当于模糊优选模型。

2.2 确定各指标的相对隶属度[6]

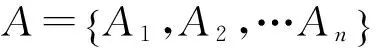
(8)

(9)

(10)

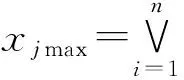
2.3 确定各指标的组合权重

确定各个指标的权重是选择模型的首要问题。目前，评价指标的权重主要有主观、客观和组合权重3种。为确保EPC项目总承包商选择更加合理可靠，选择过程中的主、客观因素理应得到综合全面的考虑。因此，根据最小相对信息熵原理，将由层次分析法确定的主观权重和信息熵法确定的客观权重进行组合得到各指标的组合权重[7]，以确保选择结果真实公正。

2.3.1AHP法确定主观权重[8,9]

首先构造各层次指标的判断矩阵(主要是依据前文建立的递阶层次指标体系及各层次指标两两相比的重要性)。由此根据各判断矩阵的最大特征值求出其对应的特征向量，并对其进行归一化处理和一致性检验，若一致性检验通过即可得到相应的主观权重向量Wz。则一级指标的主观权重向量为

且满足

2.3.2 利用信息熵法确定客观权重[10]

目前信息熵法常被用来客观地确定指标的权重其具体步骤如下。

(1) 首先通过对不同总承包商在各指标下的特征目标值组成的矩阵X进行归一化处理得到计算矩阵。为反映评价体系中各评价指标的相对重要性，应根据要评价的问题，将各指标作无量纲化处理，本文采用指标相对隶属度矩阵R作为其计算矩阵。

(2) 计算第i个总承包商Ai在第j个指标下的指标值比重pij。

(11)

(12)

式中，ej为第j个指标值。

(4) 计算各评价指标的客观权重。

(13)

式中，wj为第j个指标的客观权重(j=1,2,…,m)。

2.3.3 确定组合权重[11,12]

(14)

式中， wj为第j个指标的组合权重； wzj为第j个指标的主观权重；wkj为第j个指标的客观权重。

对上述问题进行求解可得出组合权重为

(15)

3 实例分析

实施EPC总承包模式的W水利工程，业主拟采用邀请招标的方式选择合适的总承包商。要从6家备选的总承包企业中筛选出最为可靠的3家，并对其发出招标邀请。有关各总承包企业的基本情况如表1所示。表中无法量化的定性指标的特征目标值由相关专家根据总承包商的实力，采用10分打分法，对其进行量化[2]。

表1 各总承包企业对应不同指标的特征目标值

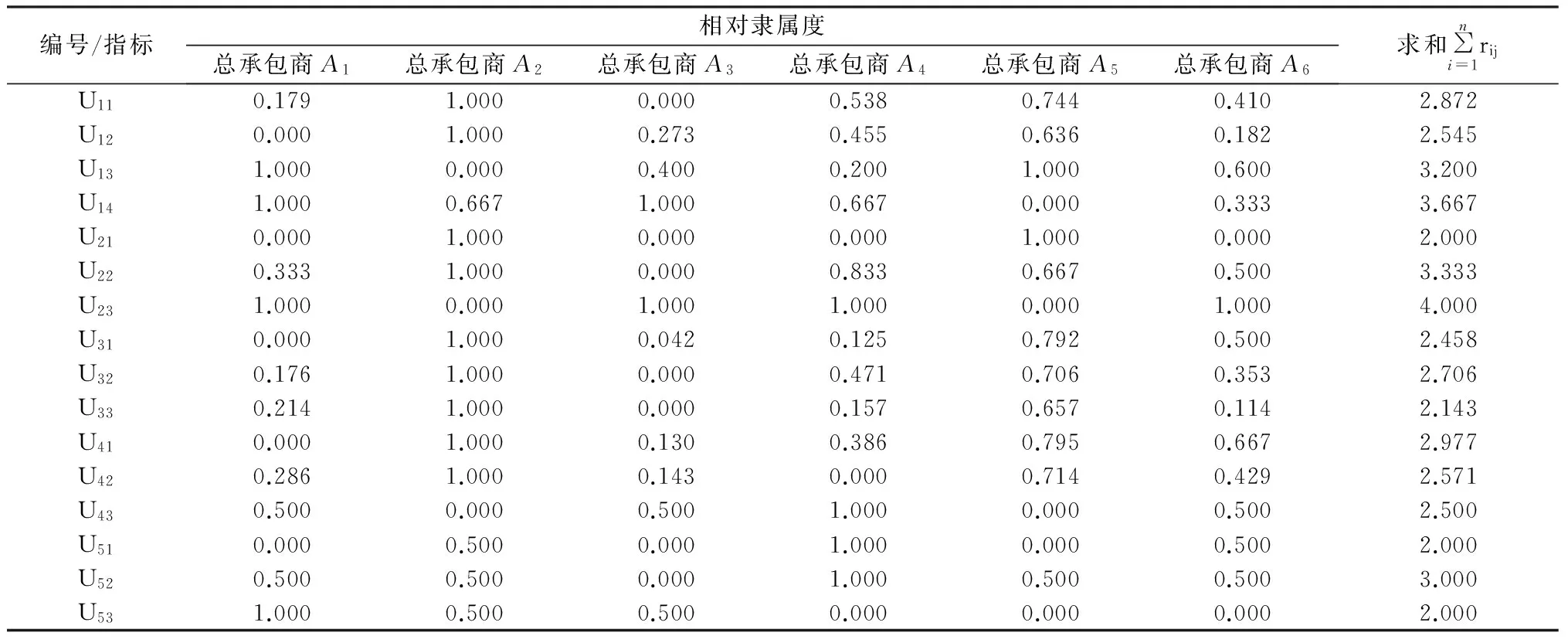
表2 各评价指标下不同总承包商的相对隶属度

3.1 确定各指标的相对隶属度

根据2.2中的公式(8)～(10)计算出的各总承包商在各评价指标下的相对隶属度如表2所示。

3.2 主客观组合权重的确定

3.2.1 确定主观权重

根据2.3.1中层次分析法确定主观权重的具体方法及相关专家的打分情况，可得出各评价指标的主观权重向量为

Wz={0.097,0.027,0.074,0.098,0.038,0.010,0.061,0.258,0.049,0.091,0.027,0.020,0.072,0.072,0.060,0.019}

3.2.2 确定客观权重

(1) 根据2.3.2中的公式(11)计算第i个总承包商在第j个指标下的指标值所占的比重。以总承包商A1和指标U11为例，则有

其余各指标下不同总承包商的指标值所占的比重如表3所示。

(2) 根据2.3.2中的公式(12)计算得出各指标的熵值ej，然后根据公式(13)计算各评价指标的客观权重，其中假定当pij=0时，pijlnpij=0。表4即为各指标的客观权重。

3.2.3 确定主客观组合权重

将3.2.1和3.2.2中求得的主客观权重代入2.3.3中的公式(15)，由此可以求解出各指标的组合权重，如表5所示。

表3 各指标下不同总承包商的指标值比重pij

表4 指标U11～ U53的客观权重

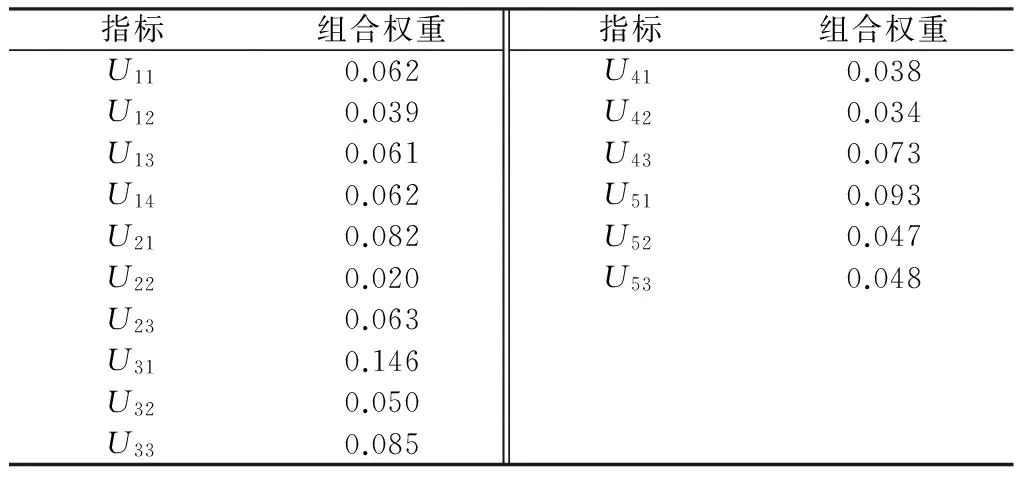
表5 指标U11～ U53的组合权重

3.3 模型的选择结果

将3.1中确定的各指标的相对隶属度和3.2中计算的主客观组合权重代入2.1的模型公式中，计算出不同α和p组合所得的4个不同选择模型下各总承包商的综合优属度，见表6。

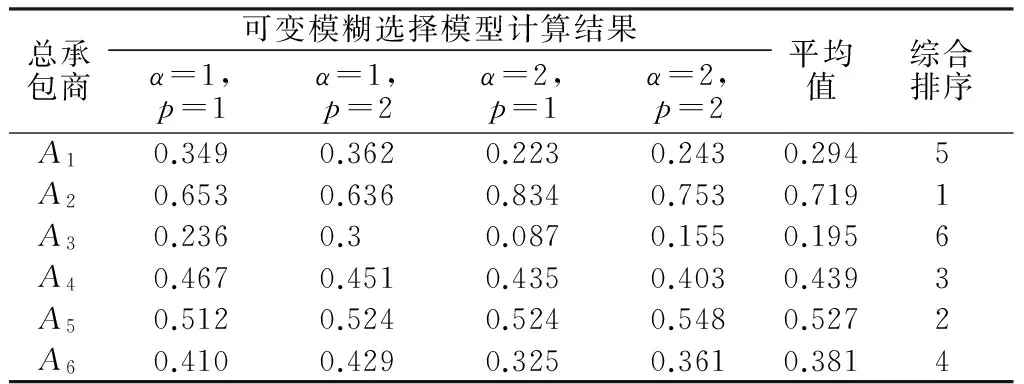
表6 可变模糊选择模型计算结果

根据表中可变模糊选择模型的计算结果，可求出不同总承包商在4种选择模式下综合优属度的平均值及其优劣排序。结果表明，关于W水利工程在EPC模式下总承包商的选择，业主应向总承包商A2、A5、A4三家企业发出邀请招标。事实证明，最终结果与实际情况比较吻合，该选择方法对于EPC项目总承包商的选择具有一定的有效性和可行性。

4 结 语

运用可变模糊决策模型，建立业主选择EPC项目总承包商的选择模型，先后运用AHP和信息熵法，分别计算各指标的主、客观权重，并根据最小相对信息熵原理对其进行组合[11]；通过各指标的指标值矩阵X，求得其对应的隶属度矩阵；将指标的主客观组合权重及其相对隶属度数据代入可变模糊决策模型中，得出EPC项目总承包商的选择方案；最后，将该选择模型应用于W水利工程实例中，对6个备选总承包商企业的综合优属度进行优劣排序，确定业主的选择对象。

将基于可变模糊决策理论的选择模型及主客观组合权重应用于EPC项目总承包商的选择问题中，使所得评价结果更加全面，且弥补了由个人主观臆断带来的缺陷。实例结果表明，该选择模型得到的评选结果与实际中选择方案契合，是业主选择EPC项目总承包商时可以考虑的有效方法之一。

[1] 赵启.EPC项目选择承包商研究[D].北京:清华大学,2005.

[2] 王显鹏,贾增科.基于Vague集的EPC项目总承包商选择模型研究[J].项目管理技术,2011,9(6):13-16.

[3] 杨晓辉.绿色理念下EPC项目总承包商选择研究[D].哈尔滨:哈尔滨工业大学,2011.

[4] 孟宪海,赵启.EPC项目选择总承包商的原则与标准[J].经贸实务,2005,(7):55-57.

[5] 陈守煜.水资源与防洪系统可变模糊集理论与方法[M].大连:大连理工大学出版社,2005.

[6] 陈守煜.复杂水资源系统优化模糊识别理论与应用[M].长春:吉林大学出版社,2002.

[7] 李秋元,刘东.组合权重模糊模型在区域地下水水质评价中的应用[J].中国农村水利水电,2014,(3):1-4.

[8] 方国华,黄显峰.多目标决策理论、方法及其应用[M].北京:科学出版社,2011.

[9] 王方勇,穆征,李静,等. 基于模糊AHP分析法的水库移民环境容量分析[J]. 人民长江,2009,40(13):66-68.

[10]罗进.利用信息熵计算评价指标权重原理及实例[J].武汉纺织大学学报,2014,27(6)：86-89.

[11]文俊,李靖,金菊良，等.基于熵组合权重的区域水资源可持续利用预警模型[J].水电能源科学,2006,(3):6-10.

[12]吴开亚,金菊良.区域生态安全评价的熵组合权重属性识别模型[J].地理科学,2008,(6):754-758.

(编辑：唐湘茜)

2017-01-10

张元节，女，华北水利水电大学水利学院，硕士研究生.

1006-0081(2017)02-0027-05

TV512

A