半径自适应的初始中心点选择K-medoids聚类算法

王 勇，王李福，饶勤菲，邹 辉

(重庆理工大学 计算机科学与工程学院，重庆 400054)

半径自适应的初始中心点选择K-medoids聚类算法

王 勇，王李福，饶勤菲，邹 辉

(重庆理工大学 计算机科学与工程学院，重庆 400054)

针对K-medoids(K为中心点)聚类算法对初始聚类中心敏感、聚类结果依赖于初始聚类中心的缺陷，提出一种新的半径自适应的初始中心点选择算法。该算法在每次迭代过程中都重新根据剩余样本点的分布特征计算半径，从而实现动态计算相应样本点的局部方差和领域半径，选取较优的初始聚类中心点，实现良好的聚类效果。采用不同规模的UCI数据集和不同比例随机点的模拟数据集进行测试，利用5个通用的聚类评价指标对性能进行评价。结果表明：本算法性能较同类算法有明显提高。

局部方差；初始聚类中心；聚类；K-medoids;自适应

聚类在机器学习及模式识别中已经成为研究的热点，其在生物信息学、文本检索、医学图像处理、网络入侵检测等领域有着广泛的应用[1-3]。目前聚类的方法主要分为以下几类：基于层次的方法、基于密度的方法、基于网格的方法、基于模型的方法、基于划分的方法和高维数据的方法[4-5]。其中，K-medoids聚类算法是基于划分的经典聚类算法之一[6]，因其对噪声敏感性较低得到了较多的应用[7]。然而，K-medoids聚类算法存在无法事先确定合适的聚类数目、算法复杂度较高、容易达到局部最优、没有统一的聚类评价准则函数、初始中心点选择误差较大等缺陷[8]。为克服传统K-medoids算法在初始聚类中心点选择方面的不足，姚丽娟[5]通过矩阵方式求解高密度区域进行初始中心点选取，从而缩小了初始中心点搜索范围，降低了算法复杂度，但其需要设置一个经验值θ来计算平均密度Mdensity，通过Mdensity的计算确定初始中心点的选择范围。马菁等[9]提出了一种基于粒度的样本相似度函数来选取初始中心点的思路，避免了传统K-medoids聚类算法中很多不必要的中心点迭代计算，但其算法中阈值d的确定没有可以度量的数学方法。谢娟英[10]通过对邻域半径的确立直接选取最大密度的样本点作为初始中心点。当数据规模较大时，该算法相比传统的K-medoids聚类算法时间复杂度低，但是邻域半径大小只是一个经验值，缺乏一定的理论指导。文献[11]通过对邻域周围样本点个数Num的设置来计算方差，并以方差作为半径来确定初始中心点的选择范围，从而在一定程度提高了聚类的准确性。不同的Num值对样本的邻域集合、局部方差大小有不同的影响，然而在定义所有样本局部方差以及样本邻域集合时采用的是同一个值，并没有考虑到样本局部分布特征的不同对初始中心点选择的影响。

为保证选取的初始聚类中心点尽可能位于不同的类簇，文献[11]虽然采用了统一的Num值，考虑到了全局最优的情况，但是好的聚类初始中心点选择过程中既要考虑到全局最优又要考虑到局部最优，采用统一的Num值计算各个样本点的邻域半径没有考虑到各样本局部分布特征的不同，因此更好的Num不应当是一个固定的值，而应既能考虑到全局的最优解，又能伴随着局部样本分布的变化而变化，具有自适应的效果。本文提出了一种根据每一个样本点的分布特征优化局部方差和邻域半径的方法。为考虑全局分布特性，该方法通过全局半径确定Num值，尽可能获得全局最优解。同时考虑到各个样本局部分布特征的不同，选用在同一个半径范围外样本点的数量作为每一个样本的Num值，不同的样本分布特性将会得到不同的Num值，从而重新定义样本的局部方差和邻域半径。该方法能动态计算出相应样本点的邻域半径，通过对邻域半径的确立，选取出较优的初始聚类中心点。

1 基于局部方差的K-medoids算法

基于局部方差的K-medoids算法[10]思想来源于概率论和数理统计。当数据在平均数附近波动较大时，各数据与平均数之差的平方和较大，方差较大；反之则方差较小。根据定义，位于数据分布较为集中的区域或者中心区域方差较小。为了寻找较好的初始聚类中心，选择的K个初始聚类中心不但要尽可能处于K个类簇的中心区域，而且应尽量分别位于K个类簇，既保证初始聚类中心位于样本分布密集区域，同时保障初始聚类中心位于不同的类簇。算法选取初始中心点的详细步骤如下：

步骤1 输入K，X，Num(其中K为类簇数，X为数据集，Num值为近邻样本参数)。

步骤2 计算X中各个样本点xi的局部方差F(xi)，依据F(xi)值将X中的样本按照升序排列，得到样本集X′，同时初始化聚类中心点集M为空，即M={}。

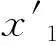
步骤5 如果M中包含有K个中心点，即|M|=K，则转步骤6，否则转步骤3。

步骤6 输出初始中心点集M。

该算法在定义样本局部方差和邻域半径时采用统一的Num值，并未考虑样本局部分布特征的不同对初始中心点选取的影响。虽然与传统聚类算法相比聚类效果有一定提高，但当其采用相同Num值计算样本点的邻域半径时，可能会造成两种情况：一是邻域半径过大，把不该删除的样本点即下一个待选取的中心点删除，从而影响初始中心点的选取；二是邻域半径过小，该删除的样本点未能删除，反而被选为下一个中心点，影响初始中心点的选取。同时，人为选取Num经验值也会增加操作复杂度。

2 新的基于局部方差的K-medoids算法

为解决选取的初始聚类中心点既要考虑全局最优又要考虑局部最优的问题，本文提出一种根据每一个样本点的分布特征优化局部方差和领域半径的方法，可以选取出较优的初始聚类中心点。

2.1 相关定义如下

Radius值定义为：

(1)

样本xi周围样本点个数的Num值定义为：

Num=num[d(xi-xj)>t×Radius]

(2)

其中，t为从0到10步长为1的半径调节系数。

样本xi的局部方差定义为

(3)

样本xi的邻域半径定义为

(4)

neigh(xi)={xl|d(i,l)≤L1

l=1,2,…,n}

(5)

2.2 算法详细步骤

本算法分为4个阶段，流程框架如图1所示。

图1 算法流程框架

算法的详细步骤如下：

a) 初始化聚类中心

步骤1 根据式(1)计算所有样本点之间的平均距离作为Radius值，同时初始化聚类中心点集M为空，即M={}。

步骤2 每个样本点以t×Radius作为半径，根据式(2)计算得到n个样本点各自的Num值，步骤如下：

① 令Num=0；

② 计算dj到di的距离dij，j=1,2,…,n；

③ 若dij>t×Radius，则Num++。

步骤3 根据式(3)计算每个样本点的局部方差，再根据式(4)得到每个样本点的邻域半径。

步骤4 取局部方差最小的样本点作为初始聚类中心点，并加入到集合M中。

步骤5 按照式(4)和(5)删除该中心点及其邻域半径内的样本点。

步骤6 重复步骤2～5，直到初始中心点集M中包含有K个中心点，即|M|=K。

步骤7 输出中心点集M。

b) 构造初始类簇

步骤1 将X中所有样本点分配给M中距离最近的中心点，得到初始类簇划分。

步骤2 计算聚类误差平方和。

c) 更新类簇中心点

步骤1 在每一个类簇中重新计算每个样本点到其他样本点的距离，将距离和最小的样本点作为新的类簇中心点。

步骤2 用新中心点替换原来的中心点。

d) 重新分配数据

步骤1 在X中计算每个样本点到M中每个中心点的距离，将样本分配到距离最近的中心点所在的类簇。

步骤2 计算当前类簇的聚类误差平方和，若没有变化，则转步骤c)继续执行，连续计算10次若没有变化，则算法结束；否则转步骤c)继续执行。

3 实验仿真分析

为测试本文算法的聚类性能，分别采用UCI机器学习数据库[12]的经典数据集和含有不同规模、不同比例的模拟数据集进行实验。实验配置为Pentium(R) Dual-Core E5800 3.20GHz CPU,48G内存，500G硬盘，Win7 64位操作系统的高性能计算机，使用Java语言在Myeclipse 10.0开发环境下进行算法实现。将改进后的K-medoids算法与改进前的K-medoids算法[10-11]进行实验对比。

算法性能评价采用5个通用的聚类评价指标：聚类误差平方和、RI指数、Precision、Recall、F1值。若TP为同一类的样本点被分到同一个簇，TN为不同类的样本点被分到不同簇，FP为不同类的样本被分到同一个簇，FN为同一类的样本被分到不同簇，则有：

RI=(TP+TN)/(TP+FP+FN+TN)

(6)

Precision=TP/(TP+FP)

(7)

Recall=TP/(TP+FN)

(8)

F1=2×Recall×Precision/(Recall+Precision)

(9)

3.1 UCI机器学习数据库数据集实验

采用UCI数据库[12]常用的10个经典测试数据集进行测试，包括Iris、Wine、WDBC等。其中，大数据集选用包含2 310个样本的Soybean-small数据集。数据集见表1，表中最后一列t为调节系数。

表1 数据集描述及相应的t值

图2显示了不同算法在不同数据集上的测试评价指标。通过实验结果比较可见：在数据集2(Iris)上除聚类误差平方和指标外其余各指标低于另外两个算法；数据集3(Wine)上Precision指标略低于另外两个算法，但是其余5个指标均优于Xie和Gao的算法；在数据集1(Soybean-small)上Recall指标低于其余两种算法，其余5个指标均优于Xie和Gao的算法。在剩余的4个数据集中，5项指标均大幅优于另外两种算法。

以上关于UCI数据集的实验结果分析表明：本文算法优于改进前算法，有效改进了聚类效果，同时算法的伸缩性也有所提高。

3.2 人工模拟数据集实验

表2 随机生成的带随机点的人工模拟数据集的生成参数

图3显示了不同算法在不同模拟数据集上的评价指标。由实验结果比较可见：在随机样本比例为20%的小规模数据集以及随机样本比例分别为10%，15%的大规模数据集上，3种算法聚类性能评价指标相当；在其余的数据集上，本文算法均大幅优于改进前算法和基于邻域的K中心点聚类算法。从图中还可以看出：另外两种算法出现较大波动性，说明本文算法较少受到随机性点的影响，聚类效果更稳定。

以上模拟数据集实验结果显示：本文算法聚类效果更稳定，对含有随机性样本点的数据集有更好的聚类效果。

图2 UCI数据集的聚类结果比较

Fig.2 Comparison of clustering results on UCI datasets

图3 不同比例随机点人工模拟数据集上实验结果

4 结束语

本文针对现有K-medoids聚类算法的不足，提出了一种半径自适应的初始中心点选择K-medoids 聚类算法。该算法结合了样本的全局分布特征与局部分布特征，重新对局部方差和邻域半径进行了优化，从而提高了原聚类算法的性能。在UCI数据集以及含有不同比例随机点的不同规模模拟数据集上的测试结果表明：本文算法可伸缩性较好，在含有不同比例随机点的数据集中有更好的聚类效果，说明本文算法聚类效果较好。

[1] 王勇，唐靖，饶勤菲，等.高效率的K-means最佳聚类数确定算法[J].计算机应用,2014,34(5):1331-1335.

WANG Yong,TANG Jing,RAO Qinfei,et al.High efficient K-means algorithm for determining optimal number of clusters[J].Journal of Computer Applications,2014,34(5):1331-1335.

[2] 陈庄，罗告成.一种改进的K-means算法在异常检测中的应用[J].重庆理工大学学报(自然科学),2015,29(5):66-70.

CHEN Zhuang,LUO Gaocheng.Improved K-means Algorithm Using in Anomaly Detection[J].Chongqing University of Technology(Natural Science),2015,29(5):66-70.

[3] 刘云.中文文本关键词提取和文本聚类中聚类中心点选取算法研究[D].镇江:江苏大学,2016.

LIU Yun.Research on Keyword Extraction Algorithm for Chinese Texts and Cluster Center Point Selection Algorithm in Text[D].Zhenjiang:Jiang Su University,2016.

[4] 孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.

SUN Jigui,LIU Jie,ZHAO Lianyu.Clustering algorithm research[J].Journal of Software,2008,19(1):48-61.

[5] 金建国.聚类方法综述[J].计算机科学,2014,41(11A):288-293.

JIN Jianguo.Review of Clustering Method[J].Computer Science,2014,41(11A):288-293.

[6] 姚丽娟，罗可，孟颖.一种新的k-medoids聚类算法[J].计算机工程与应用,2013,49(19),153-157.

YAO Lijuan,LUO Ke,MENG Ying.Newk-medoids clustering algorithm[J].Computer Engineering and Applications,2013,49(19):153-157.

[7] 朱晔，冯万兴，郭钧天,等.一种改进的K-中心点聚类算法及在雷暴聚类中的应用[J].武汉大学学报(理学版),2015,61(5):497-502.

ZHU Ye,FENG Wanxing,GUO Juntian,et al.ImprovedK-Medoids Algorithm Based on Density Information for Thunderstorm Clustering[J].Journal of Wuhan University(Nat Sci Ed),2015,61(5):497-502.

[8] 潘楚，张天伍，罗可.两种新搜索策略对K-medoids聚类算法建模[J].小型微型计算机系统,2015,36(7):1453-1457.

PAN Chu,ZHANG Tianwu,LUO Ke.ModelingK-medoids Clustering Algorithm by Two New Search Strategies[J].Journal of Chinese Computer Systems,2015,36(7):1453-1457.

[9] 马菁，谢娟英.基于粒计算的K-medoids聚类算法[J].计算机应用,2012,32(7):1973-1977.

MA Jing,XIE Juanying.New K-medoids clustering algorithm based on granular computing[J].Journal of Computer Applications,2012,32(7):1973-1977.

[10]谢娟英，郭文娟，谢维信.基于邻域的K中心点聚类算法[J].陕西师范大学学报(自然科学版),2012(7):16-22.

XIE Juanying,GUO Wenjuan,XIE Weixin.A neighborhood-based K-medoids clustering algorithm[J].Journal of Shanxi Normal University(Natural Science Edition),2012(7):16-22.

[11]谢娟英，高瑞.Num-近邻方差优化的K-medoids聚类算法[J].计算机应用研究,2015,32(1):30-34.

XIE Juanying,GAO Rui.OptimizedK-medoids clustering algorithm by variance of Num-near neighbor[J].Application Research of Computers,2015,32(1):30-34.

[12]FRANK A,ASUNCOIN A.UCI machine learning repository[EB/OL].[2016-10-12].http://archive.ics.uci.edu/ml.

(责任编辑 杨黎丽)

Radius-Adaptive on Selection of Initial Centers inK-Medoids Clustering

WANG Yong, WANG Li-fu, RAO Qin-fei, ZOU Hui

(College of Computer Science and Engineering, Chongqing University of Technology, Chongqing 400054, China)

For the defect ofK-medoids clustering algorithm which was sensible to the initial center and depended on the initial center, this paper proposed a new selection of initial centers algorithm through radius adaptive. The algorithm calculated each radius according to distribution of the remaining sample in each iteration, thus to dynamically calculate local variance and neighborhood radius for corresponding sample and then select the optimum initial cluster centers to achieve good clustering effect. Using different size of UCI data sets and simulated data sets with different ratios of random points for testing and using the five general clustering index to evaluate its performance, the results show that the performance of this algorithm is better than other similar algorithms.

local variance; initial cluster center; clustering algorithm;K-medoids; adaptive

2016-11-20 基金项目：国家自然科学基金资助项目(61173184)

王勇(1974—)，男，重庆人，博士，副教授，主要从事多媒体和网络研究，E-mail： ywang@cqut.edu.cn；通讯作者 王李福(1989—)，男，重庆垫江人，硕士研究生，主要从事图像处理研究,E-mail: hellowanglifu@163.com。

王勇，王李福，饶勤菲，等.半径自适应的初始中心点选择K-medoids聚类算法[J].重庆理工大学学报(自然科学)，2017(2):95-101.

format：WANG Yong, WANG Li-fu, RAO Qin-fei, et al.Radius-Adaptive on Selection of Initial Centers inK-Medoids Clustering[J].Journal of Chongqing University of Technology(Natural Science)，2017(2):95-101.

10.3969/j.issn.1674-8425(z).2017.02.017

TP301

A

1674-8425(2017)02-0095-07