顶部溶洞水压对隧道突涌水灾害影响的数值分析

雷 霆， 关 欣， 洪 帆， 居炎飞， 韩劲龙， 李乐乐

(1. 武汉港湾工程质量检测有限公司， 湖北 武汉 430040； 2. 海工结构新材料及维护加固技术湖北省重点实验室， 湖北 武汉 430040)

顶部溶洞水压对隧道突涌水灾害影响的数值分析

雷 霆1, 2， 关 欣1， 洪 帆1， 居炎飞1, 2， 韩劲龙1, 2， 李乐乐1, 2

(1. 武汉港湾工程质量检测有限公司， 湖北 武汉 430040； 2. 海工结构新材料及维护加固技术湖北省重点实验室， 湖北 武汉 430040)

岩溶地区地质条件复杂，在隧道修建中存在溶洞突涌水安全隐患，而顶部溶洞带来的灾害性更加明显，溶洞水压是其重要影响因素。针对隧道顶部溶洞，建立数值模型，将溶洞水压作为工况因素，分析围岩中的孔隙水压力变化规律，揭示隧道开挖过程中突涌水通道的分布情况。基于数值模型中单元孔隙水压力突变最大值判断方法，溶洞与掌子面围岩达到塑性状态后，监测两者之间的单元孔隙水压力随开挖步变化速率，找出每一行单元中的最大值，从而确定不同溶洞水压下的突水通道及安全厚度。研究表明，随着顶部溶洞水压增大，突水通道距离溶洞底部由近及远，而安全厚度也随之增大。

岩溶隧道； 顶部溶洞； 溶洞水压； 突水通道； 安全厚度

0 引言

我国岩溶地区分布广阔，随着高速公路、铁路的迅猛发展，穿越岩溶山区的隧道越来越多，这些隧道具有大埋深、高地应力、强岩溶等地质特点。由于地质条件复杂，难以通过勘察手段明确地质灾害体的分布情况，常常会带来突水涌泥等灾害，给隧道开挖和运行造成严重的威胁。

溶洞是岩溶灾害中最常见的致灾构造，由于隧道开挖扰动，防突厚度减小，溶洞中的充填水压得到释放，容易造成强突水。隧道顶部的溶洞及其充填物在地应力、开挖扰动双重作用下，极易发生突水涌泥，具有爆发性强、体量大及垮塌伤害等特点，破坏力极大。史世雍等[1]通过建立有限元模型，分析了隧道顶部溶洞对围岩稳定性的影响规律，证明拱顶最大主应力随开挖下降比较明显；赵明阶等[2]、宋战平等[3]揭示了隧道上部溶洞的距离及大小与隧道顶部围岩塑性区的大小及沉降量成一定相关关系。

溶洞的致灾机制复杂，涉及到溶洞赋存规律、充填物特性以及围岩情况。文献[4-7]表明溶洞致灾主要体现在溶洞与隧道掌子面之间围岩，溶洞周围岩体承受溶洞水压及地应力作用，沿岩体软弱结构面产生渗透破坏，逐渐达到塑性状态，而掌子面围岩受到开挖扰动产生裂隙使强度降低而进入塑性变形状态，随着开挖的推移，两者塑性区产生贯通，带来突水的风险。李利平等[8]通过数值方法对岩体应力场、渗流场和损伤场进行耦合分析，研究表明突水通道的形成经历了隔水岩体裂纹萌生、扩展和贯通。由此可见，溶洞与掌子面之间岩体塑性区贯通后仍具有一定的承受水压和地应力的能力，当一定开挖步后，岩体强度降低而通道形成，发生突水。

溶洞与隧道之间安全厚度对溶洞隐伏隧道开挖具有现实指导意义，当前学者对安全厚度研究较多，而常见的方法主要是基于数值手段而衍生的预测方法，有数值流行方法、多元线性回归、正交分析、支持向量机等[9-12]，提供了多种安全厚度的预测方法，总结的安全厚度也有利于不同围岩情况下隧道突水风险的规避。

本文以隧道顶部溶洞为研究对象，研究溶洞水压对突水通道的影响，基于数值模型中单元孔隙水压力突变最大值判断方法，即溶洞与掌子面围岩达到塑性状态后，监测两者之间的单元孔隙水压力随开挖步的变化速率，随着开挖继续进行，当水平向每一行单元均先后达到最大值时，认为达到破坏，产生突水通道，即可确定突水通道及安全厚度。通过研究可以确定上覆溶洞突水随隧道开挖过程的演变及致灾过程，可为隧道及地下工程提供突水风险的预先判断及规避的预留时间。由于本文并不以数值结果作为工程应用目的，而是定性描述突水通道的形成原理及溶洞水压对围岩的影响情况，因而参考文献[13-14]，将溶洞距离设置为2 m。

1 隧道计算模型及模拟方案

本文利用有限元软件Ansys 12.0建立三维隧道模型，并导入FLAC 3D有限差分软件进行开挖模拟。

1.1 计算模型及边界条件

根据隧道结构的计算原理及相关案例经验，并考虑到模型边界效应、隧道埋深及溶洞距离，确定本文几何模型： 1)隧道中心位置取x=0，y=0，z=0，隧道跨度取12 m； 2)水平方向(x方向)正负各取25 m； 3)垂直方向(y方向)正向取40 m(其余埋深高度以竖向荷载施加在模型顶部进行等效模拟)，负向取25 m； 4)纵向(z方向)沿负向取46 m； 5)溶洞以球体进行简化模拟，位置设在纵向中点处，即z=-23 m。网格统一采用映射网格划分，溶洞部分在建模过程中预先保留，建立模型如图1所示，模型网格单元约为100 000，主要表现为隧道断面以及溶洞区域密集，向四周逐渐变为稀疏，满足模型计算要求。

图1 模型网格划分

模型边界条件约束： 下边界施加竖向位移约束，左右边界施加水平位移约束，前后边界施加轴向位移约束。

1.2 模型参数选定

1.2.1 地质力学参数

模型地质力学参数取值如表1所示。隧道采用全断面法开挖，为了更加直观反映隧道溶洞突水危害性，未进行隧道开挖支护研究，隧道掌子面轮廓设为不透水边界。模型的地下水头统一取50 m。

表1 模型地质力学参数

隧道埋深h取300 m，溶洞半径R取6 m，溶洞与隧道之间距离d取2.0 m，溶洞充填水压分为5个档，分别取p=0.10、0.25、0.50、0.75、1.00 MPa。

1.2.2 流体渗透参数

模型设计到流固耦合计算，在FLAC 3D中启用渗流模式(CONFIG fluid)，可以进行瞬态渗流分析。在该计算过程中，孔隙水压力的改变产生了变形，体积应变导致了孔隙水压力的改变，进行完全的流固耦合计算。对于隧道地下结构，地下水位影响显著，因此在模型中设置合理的浸润线(流体密度及重力加速度均相应设置)及各向同性。

流体的取值情况如下： 水的体积模量为2×109Pa，围岩的渗透系数取4.92×10-10cm/s，围岩孔隙率取0.40。

1.3 开挖与计算

在计算模型初始应力平衡时，考虑了溶洞形成过程对围岩的影响，因此采用“保留溶洞单元-杀死溶洞单元-施加溶洞水压”3次平衡方式，应用Druck-Prager屈服准则，并采用弹塑性模型进行求解。在施加溶洞水压进行平衡计算和隧道开挖情况下，采用渗流模式，模型施加一定的水头，模型6个边界面均按照水头推算的实际孔隙水压力施加，设置为透水边界，溶洞壁和隧道掌子面同样设置为透水边界。

考虑到开挖扰动及开挖步幅对溶洞渗流破坏区的影响，远离溶洞隧道两端采用3 m步幅开挖，接着2 m步幅，最后临近溶洞时为1 m步幅。具体模拟开挖步骤： 沿着开挖方向，以3 m的步幅完成第1—5步(黄色区域);以2 m的步幅完成第6—7步(绿色区域);以1 m的步幅完成第8—15步(红色区域);以2 m的步幅完成第16—17步(绿色区域);以3 m的步幅完成第18—22步(黄色区域)。隧道开挖示意图如图2所示。

图2 隧道开挖示意图(单位： m)

2 突水通道与安全厚度确定方法

由于本文采用的数值模型及参数具有一定的局限性，所产生的结果并不一定表示出现突水通道，而是定性地判断出隧道围岩与溶洞间的最危险破坏通道。基于前述突水通道形成机制，具体的确定方法如下。

1)当溶洞与隧道掌子面附近围岩的塑性区贯通时，在数值模型的贯通区水平、竖直方向上选取5×5个单元为监测点，监测其孔隙水压力随开挖步的变化情况，并计算孔隙水压力随开挖步的变化速率。隧道塑性区贯通如图3所示。

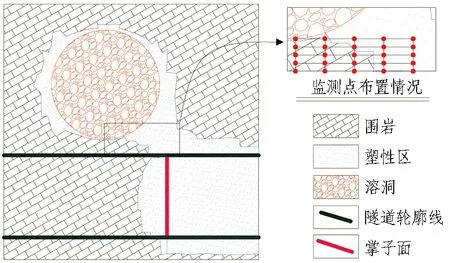
图3 隧道塑性区贯通

2)在该监测区中找出水平方向上每5个监测点中孔压速率变化最大者，可找到5个目标点，连接该目标点即成突水通道。

3)针对上述的目标点，判断其均出现陡降的开挖步，该开挖步即被确定为最危险开挖步，此时的溶洞与隧道掌子面最近的直线距离为安全厚度。安全厚度示意图如图4所示。

图4 安全厚度示意图

3 计算结果与分析

3.1 塑性区贯通情况

在不同工况下，更改FLAC 3D的计算命令流中溶洞内水压力参数，经过每一步开挖收敛计算，得到如图5所示的塑性区贯通图。

由图5可知:p=0.10、0.25、0.50、0.75、1.00 MPa工况下，开挖步分别达到第8、7、6、5、5步时塑性区产生贯通，可以初步判断溶洞内水压越大，溶洞与隧道之间围岩变形越大，塑性区贯通越早，从而突涌水风险越大。

3.2 监测点制定

选择p=0.10 MPa或0.25 MPa工况下第5开挖步下的塑性区，此时隧道与溶洞之间围岩选择范围最大，且可选单元也最多，溶洞最底部到掌子面水平分布有8组单元(V1—V8)，竖向有5组单元(H1—H5)，组成监测区，可用数列形式{i58}表示，单元具体位置及相应编号顺序如图6所示。

(a) p=0.10 MPa工况

(b) p=0.25 MPa工况

(c) p=0.50 MPa工况

(d) p=0.75 MPa工况

(e) p=1.00 MPa工况

图6 单元位置及编号

对于每种工况，为了最大覆盖监测区，使突水通道的定义更具代表性，监测点在水平、竖直向各选取5个，具体如表2所示。

表2 监测点布置情况

3.3 突水通道确定

提取不同工况下监测点的孔隙水压力，计算出单步孔隙水压力的变化速率，并绘制成曲线如图7—11所示。

由图7—11可知： 1)在p=0.1 MPa工况下，i13、i23、i34、i44、i55号单元的孔隙水压力单步突变最大，可以判处突水通道经该5个单元扩展形成； 2)在p=0.25 MPa工况下，i14、i24、i35、i45、i55号单元的孔隙水压力单步突变最大，可以判处突水通道经该5个单元扩展形成； 3)在p=0.50 MPa工况下，i15、i25、i35、i46、i56号单元的孔隙水压力单步突变最大，可以判处突水通道经该5个单元扩展形成； 4)在p=0.75 MPa工况下，i17、i27、i37、i47、i57号单元的孔隙水压力单步突变最大，可以判处突水通道经该5个单元扩展形成； 5)在p=1.00 MPa工况下，i18、i28、i38、i48、i58号单元的孔隙水压力单步突变最大，可以判处突水通道经该5个单元扩展形成。

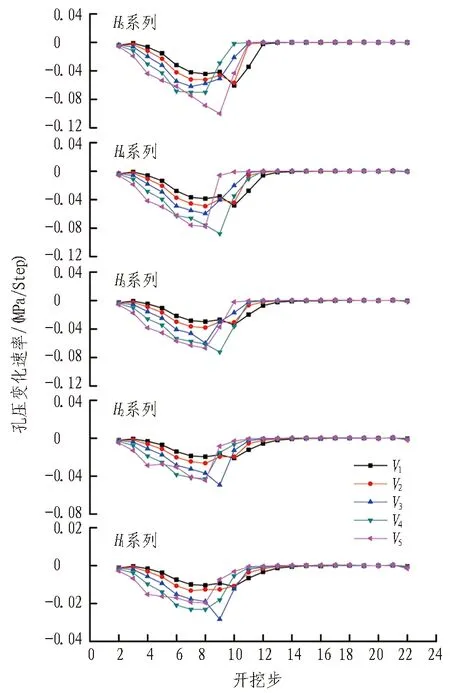
图7 监测点孔隙水压力变化速率(p=0.1 MPa)

Fig. 7 Varying velocities of pore water pressure of monitoring points (p=0.1 MPa)

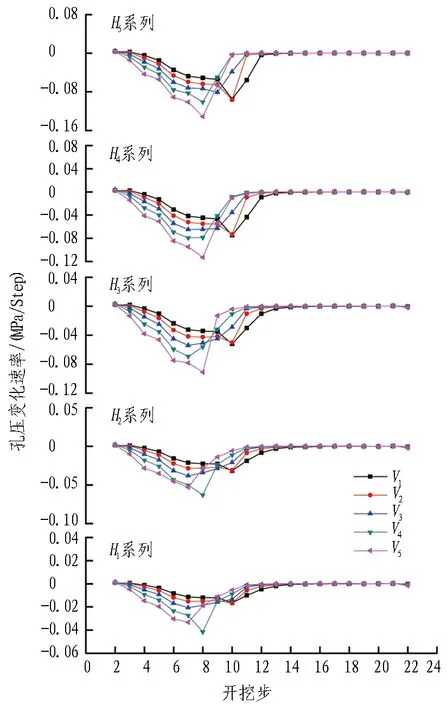
图8 监测点孔隙水压力变化速率(p=0.25 MPa)

Fig. 8 Varying velocities of pore water pressure of monitoring points (p=0.25 MPa)

图9 监测点孔隙水压力变化速率(p=0.5 MPa)

Fig. 9 Varying velocities of pore water pressure of monitoring points (p=0.5 MPa)

图10 监测点孔隙水压力变化速率(p=0.75 MPa)

Fig. 10 Varying velocities of pore water pressure of monitoring points (p=0.75 MPa)

图11 监测点孔隙水压力变化速率(p=1.0 MPa)

Fig. 11 Varying velocities of pore water pressure of monitoring points (p=1.0 MPa)

不同工况下的突水通道如图6所示。通过分析可知： 1)隧道顶部溶洞水压越大，突水通道形成的开挖步越早； 2)突水通道的上部，受溶洞水压影响较大，这是因为溶洞水压增大，附近围岩逐渐水压致裂形成通道，而离掌子面较近的地方因水压过大与掌子面附近围岩产生贯通，造成突水； 3)突水通道的下部，受溶洞水压与开挖扰动共同影响，随着溶洞水压的减小，下部通道向前移动，但比上部通道较慢； 4)溶洞水压对溶洞附近围岩的影响比掌子面附近围岩大，而开挖扰动对掌子面的围岩影响较大。

3.4 安全厚度分析

由3.3节监测点数据分析可知，不同工况下形成突水通道单元的孔隙水压力速率均达到陡降时的开挖步，即最危险开挖步，并计算出安全厚度，如表3所示。由表可知，最危险开挖步随着溶洞水压增大越早，安全厚度越大，模型中溶洞水压设计范围为 0.1～1.0 MPa，安全厚度最大为5.31 m，最小为2.24 m，该结果在实际工程中有一定的偏差，应用价值并不明显，但可以在一定程度上揭示突水通道的形成原理及溶洞水压对围岩的影响情况，借此给隧道施工带来一定的指导意义。

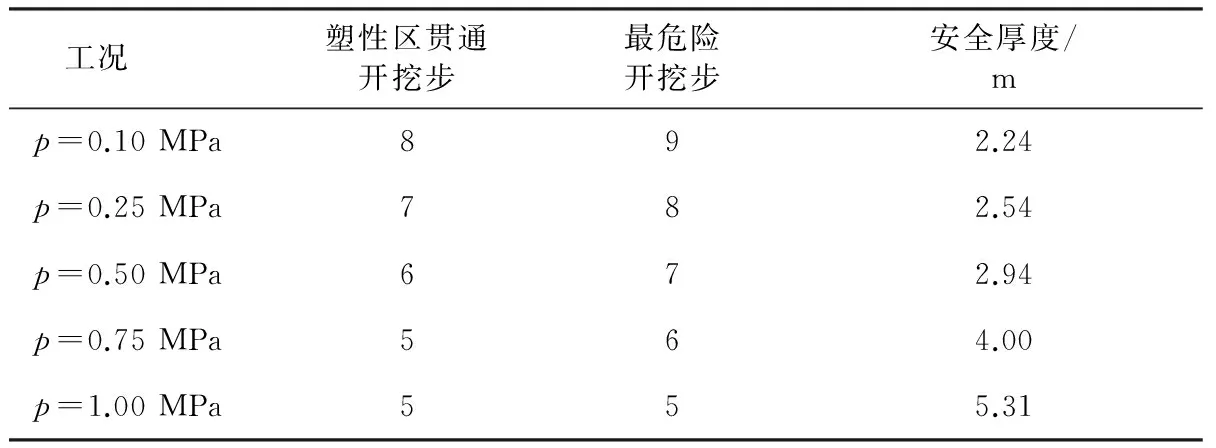
表3 安全厚度计算结果

4 结论与建议

隧道顶部溶洞对隧道的开挖极易造成突涌水灾害，为了研究溶洞水压对突水通道的影响，以溶洞水压为因素划分5种工况，基于数值分析结果，可总结如下。

1)本文建立了基于数值模型中单元孔隙水压力突变最大值判断方法，当溶洞与掌子面之间单元达到塑性状态，选择此时两者之间单位为监测对象，水平向各行单元中选一个最大突变者，竖直方向连接即为突水通道。

2)顶部溶洞水压从0.1 MPa增至1.0 MPa，突水通道距离溶洞底部由近及远，但突水通道上部位置对溶洞水压敏感度大于突水通道下部，而突水通道下部位置受开挖扰动影响较上部大。

3)溶洞与隧道之间围岩达到塑性区贯通的开挖步，随溶洞水压增大而越小，各工况下达到最危险开挖步较其塑性区贯通开挖步均有一定的延迟。通过计算可知，溶洞水压为1.0 MPa时安全厚度为5.31 m，水压为0.1 MPa时安全厚度为2.24 m，本文研究可为相关隧道工程起到一定的理论指导作用。

[1] 史世雍, 梅世龙, 杨志刚. 隧道顶部溶洞对围岩稳定性的影响分析[J]. 地下空间与工程学报, 2005, 1(5): 698-702,716.(SHI Shiyong, MEI Shilong, YANG Zhigang. Research on the influence of karst cave in the roof of tunnel on stability of surrounding rock[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(5): 698-702,716. (in Chinese))

[2] 赵明阶, 刘绪华, 敖建华, 等. 隧道顶部岩溶对围岩稳定性影响的数值分析[J]. 岩土力学, 2003, 24(3): 445-449.(ZHAO Mingjie, LIU Xuhua, AO Jianhua, et al. Numerical analysis of influence of karst caves in top of tunnel on stability of surrounding rock masses[J]. Rock and Soil Mechanics, 2003, 24(3): 445-449. (in Chinese))

[3] 宋战平, 綦彦波, 李宁. 顶部既有隐伏溶洞对圆形隧道稳定性影响的数值分析[J]. 岩土力学, 2007, 28(增刊1): 485-489.(SONG Zhanping, QI Yanbo, LI Ning. Niumerical experimentational research on concealed karst cave’s influence on circular tunnel stability[J]. Rock and Soil Mechanics, 2007, 28(S1): 485-489. (in Chinese))

[4] 李利平, 李术才, 张庆松. 岩溶地区隧道裂隙水突出力学机制研究[J]. 岩土力学, 2010, 31(2): 523-528.(LI Liping, LI Shucai, ZHANG Qingsong. Study of mechanism of water inrush induced by hydraulic fracturing in karst tunnels[J]. Rock and Soil Mechanics, 2010, 31(2): 523-528. (in Chinese))

[5] 李术才, 袁永才, 李利平, 等. 钻爆施工条件下岩溶隧道掌子面突水机制及最小防突安全厚度研究[J]. 岩土工程学报, 2015, 37(2): 313-320.(LI Shucai, YUAN Yongcai, LI Liping, et al. Water inrush mechanism and minimum safe thickness of rock wall of karst tunnel face under blast excavation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 313-320. (in Chinese))

[6] 焦阳, 白海波. 煤层底板含隐伏溶洞滞后突水机理[J]. 煤炭学报, 2013, 38(增刊2): 377-382.(JIAO Yang, BAI Haibo. Mechanism of delayed groundwater inrush from covered karst cave in coal seam floor[J]. Journal of China Coal Society, 2013, 38(S2): 377-382. (in Chinese))

[7] 张民庆, 曾强运, 杨兵. 岩溶隧道溶洞泄水机理及工程实例分析[J]. 岩土工程学报, 2010, 10(10): 1543-1550.(ZHANG Minqing, ZENG Qiangyun, YANG Bing. Water release mechanism of caverns of karst tunnels and case studies[J]. Chinese Journal of Geotechnical Engineering, 2010, 10(10): 1543-1550. (in Chinese))

[8] 李利平, 李术才, 石少帅, 等. 岩体突水通道形成过程中应力-渗流-损伤多场耦合机制[J]. 采矿与安全工程学报, 2012, 29(2): 232-238.(LI Liping, LI Shucai, SHI Shaoshuai, et al. Multi-field coupling mechanism of seepage damage for the water inrush channel formation process of coal mine[J]. Journal of Mining and Safety Engineering, 2012, 29(2): 232-238. (in Chinese))

[9] 王勇, 孙彩红. 岩溶隧道溶洞顶板安全厚度预测探讨[J]. 现代隧道技术, 2005, 42(3): 17-22.(WANG Yong, SUN Caihong. Prediction of the safe thickness of the roof of karst caves under a tunnel[J]. Modern Tunnelling Technology, 2005, 42(3): 17-22. (in Chinese))

[10] 曹文贵, 程晔, 赵明华. 公路路基岩溶顶板安全厚度确定的数值流形方法研究[J]. 岩土工程学报, 2005, 27(6): 621-625.(CAO Wengui, CHENG Ye, ZHANG Minghua. Studies of numerical manifold method for determination of safe thickness of karst roof in roadbed[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 621-625. (in Chinese))

[11] 王勇, 乔春生, 孙彩红, 等. 基于SVM的溶洞顶板安全厚度智能预测模型[J]. 岩土力学, 2006, 27(6): 1000-1004.(WANG Yong, QIAO Chunsheng, SUN Caihong, et al. Forecasting model of safe thickness for roof of karst cave tunnel based on support vector machines [J]. Rock and Soil Mechanics, 2006, 27(6): 1000-1004. (in Chinese))

[12] 刘超群, 彭红君. 隧道掌子面与溶洞安全距离分析[J]. 现代隧道技术, 2012, 49(3): 109-113.(LIU Chaoqun, PENG Hongjun. Analysis of safe distance between a tunnel and karst cave[J]. Modern Tunnelling Technology, 2012, 49(3): 109-113. (in Chinese))

[13] 郭明. 隐伏溶洞对隧道围岩稳定性的影响规律及鄂西山区岩溶处治技术研究[D]. 济南： 山东大学, 2014.(GUO Ming. Study of concealed karst cave’s influence on karst tunnel stability and treatment technology on tunnels of Exi Mountainous[D]. Jinan: Shandong University, 2014. (in Chinese))

[14] 宋建禹. 隐伏溶洞与山岭隧道间安全厚度预测及其稳定性研究[D]. 重庆： 重庆交通大学, 2012.(SONG Jianyu. Study of concealed karst caverns with mountain tunnel safety thickness prediction and the research of stability[D]. Chongqing: Chongqing Jiaotong University, 2012. (in Chinese))

Numerical Analysis of Influence of Water Pressure of Overlying Karst Cave on Tunnel Water Inrush

LEI Ting1, 2, GUAN Xin1, HONG Fan1, JU Yanfei1, 2, HAN Jinlong1, 2, LI Lele1, 2

(1.WuhanHarbourEngineeringQualityDetectionCo.,Ltd.,Wuhan430040,Hubei,China; 2.ChinaHubeiKeyLaboratoryofAdvancedMaterials&ReinforcementTechnologyResearchforMarineEnvironmentStructures,Wuhan430040,Hubei,China)

Due to the complex geological conditions of karst area, tunnel construction is often accompanied by potential safety hazard of water inrush from karst caves, especially when the karst cave overlies tunnel (in which condition the water pressure is very important). A numerical model for tunnel under a karst cave is established, and the water pressure of the karst cave is regarded as a construction condition. The variation rules of pore water pressure of surrounding rocks are analyzed, and the distribution of water inrush channel during tunnel excavation is revealed. The water inrush channel and safety thickness of rock under different water pressures of karst cave are decided based on the maximum value estimation method of mutation of the element pore water pressure. The study results show that the distance between water inrush channel and the bottom of karst cave and the safety thickness of rock increase with the water pressure of overlying karst cave increases.

karst tunnel; overlying cave; water pressure of karst cave; water inrush channel; safety thickness

2016-08-19;

2016-11-10

雷霆(1987—)，男，湖北荆门人，2015毕业于山东大学，建筑与土木工程(岩土)专业，硕士，助理工程师，主要从事岩土检测与工程方面的研究工作。E-mail： lt_paper@126.com。

10.3973/j.issn.1672-741X.2017.02.007

U 45< class="emphasis_bold"> 文献标志码： A

A

1672-741X(2017)02-0167-07