双面弹性地基梁隧道纵向变形的有限元模拟

丁志军 刘律智 潘 荣

(上海理工大学，上海 200093)

双面弹性地基梁隧道纵向变形的有限元模拟

丁志军 刘律智 潘 荣

(上海理工大学，上海 200093)

基于双面弹性地基梁模型，并借助有限元软件，分析了堆载条件下地铁隧道的纵向变形规律，考察了不同埋深、不同堆载位置对深埋隧道纵向变形的影响，结果表明，基于双面弹性地基梁模型的有限元方法分析隧道纵向变形具有可行性，埋深和堆载距离的增大都使得其对隧道纵向变形的影响逐渐减弱。

双面弹性地基梁，深埋隧道，有限元，纵向变形

0 引言

地铁作为解决城市交通拥挤问题的重要手段之一，已经在各大城市得到广泛运用。地铁的开通也会带动线路周边的发展，使得既有地铁隧道上方或其近旁越来越多的建造新结构物，从而引起地面荷载变化，土体扰动，造成隧道产生过大变形，危及隧道安全。

盾构隧道结构为主的地下线路的使用颇为广泛。盾构法隧道的构造决定其纵向承受变形的能力要小得多，因此研究地面荷载作用下隧道的纵向变形机理非常重要。林永国等[1]对地铁隧道纵向变形的影响因素进行了总结。吴庆和杜守继[2]通过室内模型试验对堆卸载作用下既有盾构隧道结构的变形特征进行研究。戴宏伟等[3]、廖少明[4]、臧小龙[5]采用不同的分析计算模型，研究了隧道内力和变形。林永国等[6]、张治国等[7]采用两阶段应力法分析基坑开挖对临近地铁隧道纵向变形的影响。白海卫[8]通过理论分析、数值模拟和原位试验等方式研究了新建隧道对既有隧道纵向结构性能的影响。然而上述研究都是基于弹性地基梁模型的隧道变形分析，现如今，地铁隧道一般都位于一定的上覆土层之下，并且随着城市地下空间的开发需求增大,地铁的深度会越来越大。此时，隧道结构的上覆土层对纵向变形的影响也不可忽略。璩继立等[9]把深埋盾构隧道等效为双面弹性地基梁，采用有限差分法和MATLAB编程求出隧道的纵向位移和内力。

本文基于双弹性地基梁理论，在文献[9]中解析解基础上，进一步的借助大型商业化有限元软件进行验证，并分析了不同堆载位置，不同埋深对于隧道纵向变形的影响。

1 基本假定与模型简介

本文采用双面弹性地基梁理论计算隧道纵向变形。基本假定和理论公式的推导已发表于文献[9]，在此不再赘述。

2 有限元算例分析

某地铁隧道附近由于施工，有一堆载区，如图1所示。荷载与隧道纵轴线平行的方向长度为L2=40 m，宽度b=30 m，超载引起的隧道上方的垂直荷载为80 kPa，荷载中心与隧道中心水平距离L1=10 m，地铁采用盾构施工，隧道埋深12 m，外径6 m，隧道截面抗弯刚度EI=9×108kN·m2，假设隧道下卧层和上覆土层的地基基床系数为k=1 000 kN/m3(具体经验值可见文献[10])。隧道分段n=40，分段长度为L=3 m。

2.1 模型网格及边界条件

按照上述算例构造有限元模型，为满足计算精度的需要，模型沿隧道轴向，即模型长120 m，隧道中心线距两侧土体边界为40 m，即宽取80 m，模型共划分了70 786个四面体单元，8 848个三角形单元，994个边单元，28个顶点单元。模型网格划分情况如图2所示。

在模型下表面，采用固定约束对X，Y，Z方向变形进行约束，在垂直于隧道中心线的两个侧面及平行于隧道中心线的两个侧面采用滑动约束分别对X方向，Y方向的变形进行约束，模型顶部为自由面，模型约束情况如图3所示。

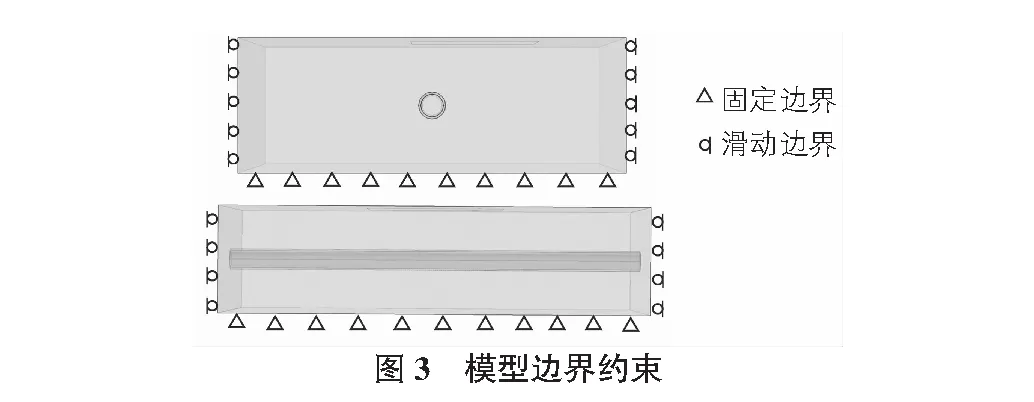
2.2 材料

隧道采用线弹性材料进行模拟，由数值解采用的隧道截面抗弯刚度等效换算，杨氏模量E1=48 GPa，泊松比μ1=0.167，密度ρ1=2 500 kg/m3。土体采用摩尔库仑模型进行模拟，杨氏模量E2=12 MPa，泊松比μ2=0.32，密度ρ2=1 850 kg/m3,粘聚力c=16 kPa，内摩擦角φ=16°。

2.3 荷载

模型荷载通过两个荷载步加载，荷载步Ⅰ：地应力平衡，在整个模型域上平衡地应力，荷载步Ⅱ：加载上部荷载，在模型上部的矩形区域内加载上部荷载80 kPa，采用斜坡函数加载形式，如图4所示。

3 有限元模拟结果

如图5所示为基于双面弹性地基梁模型的隧道纵向位移、弯矩和剪力的模拟结果。图中同时给出了文献[9]中的理论推导结果，用于对比。可以看出，有限元方法得出的结果与解析解方法得出的规律一致。例如，对于隧道沉降量，在荷载作用的中心处(x=0 m)，隧道沉降量最大，中心两边的值逐渐减小，在x=±60 m时，隧道的位移基本为0。但是，两种方法的结果大小存在差异。例如隧道沉降量的最大值分别为19.4 mm(解析解值)，23.7 mm(有限元值)，并且两者的差值在荷载作用中心处(x=0 m)最大，随着距离荷载中心越来越远，沉降量差值逐渐减小，在约x=40 m处，差值几乎为0。当距离超过40 m后，沉降量差值有稍微的增加。

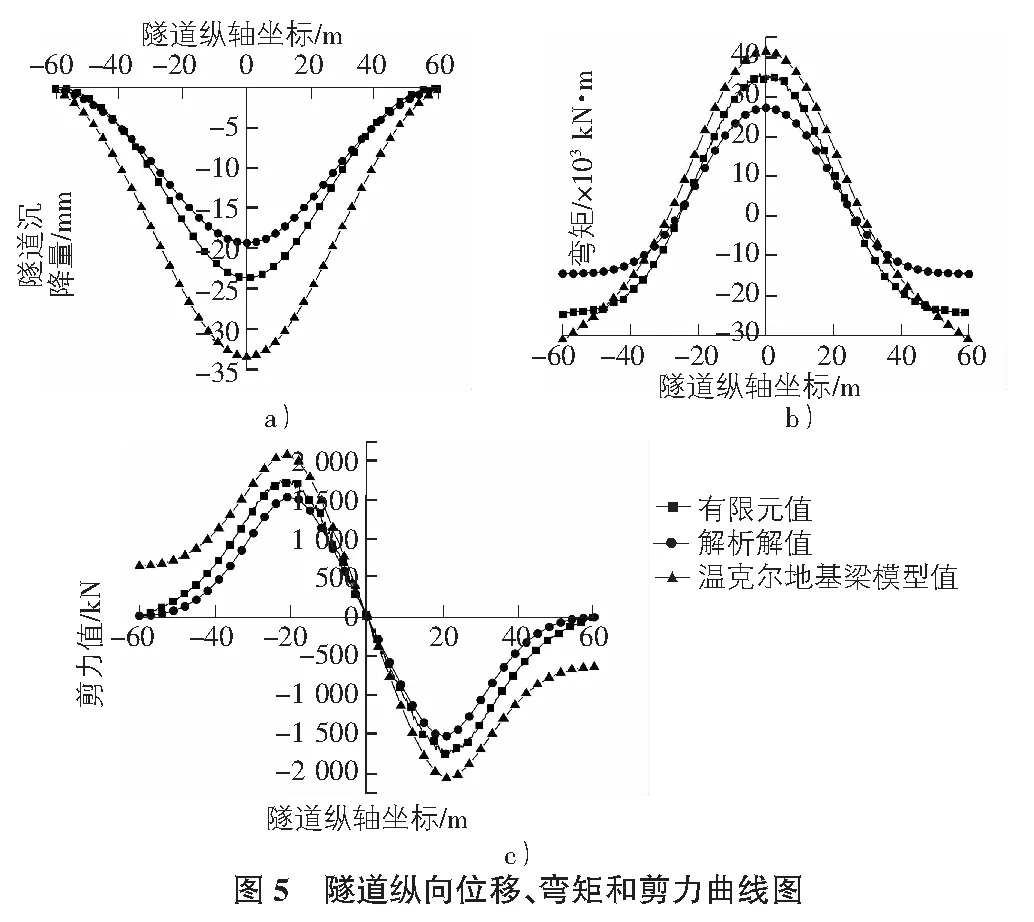
在两种不同的计算方法过程中，都做出了一定的假设。例如在有限元计算中，假设土体为理想弹塑性体，隧道采用线弹性材料进行模拟。这些假设和简化使得计算过程中出现误差以及不同方法间的差异。

虽然两种计算方法存在一定的误差及差异，但是相对于不计上覆土层影响的温克尔弹性地基梁分析方法，采用双面弹性地基梁模型计算的变形和内力，无论是解析解法，还是稍大的数值模拟法，其结果都明显要小得多。因此，采用双面弹性地基梁理论对深埋盾构隧道进行纵向变形设计要更合理。

4 不同工况的有限元模拟结果

基于上述双面弹性地基梁的有限元模型，分析了荷载位置、隧道埋深对其纵向变形的影响程度，有助于进一步了解深埋隧道的纵向变形特征。

4.1 埋深对隧道变形的影响

如图6所示为埋深分别是7 m，12 m，17 m(隧道直径保持不变)时隧道纵向变形的模拟结果。可以看出，不同埋深隧道变形的规律一致，数值不一。埋深越浅，相同位置处隧道的变形越大。因此，隧道必须具有一定的埋覆深度[11]。随着埋深的增加，隧道的最大沉降量、弯矩、剪力值迅速减小。

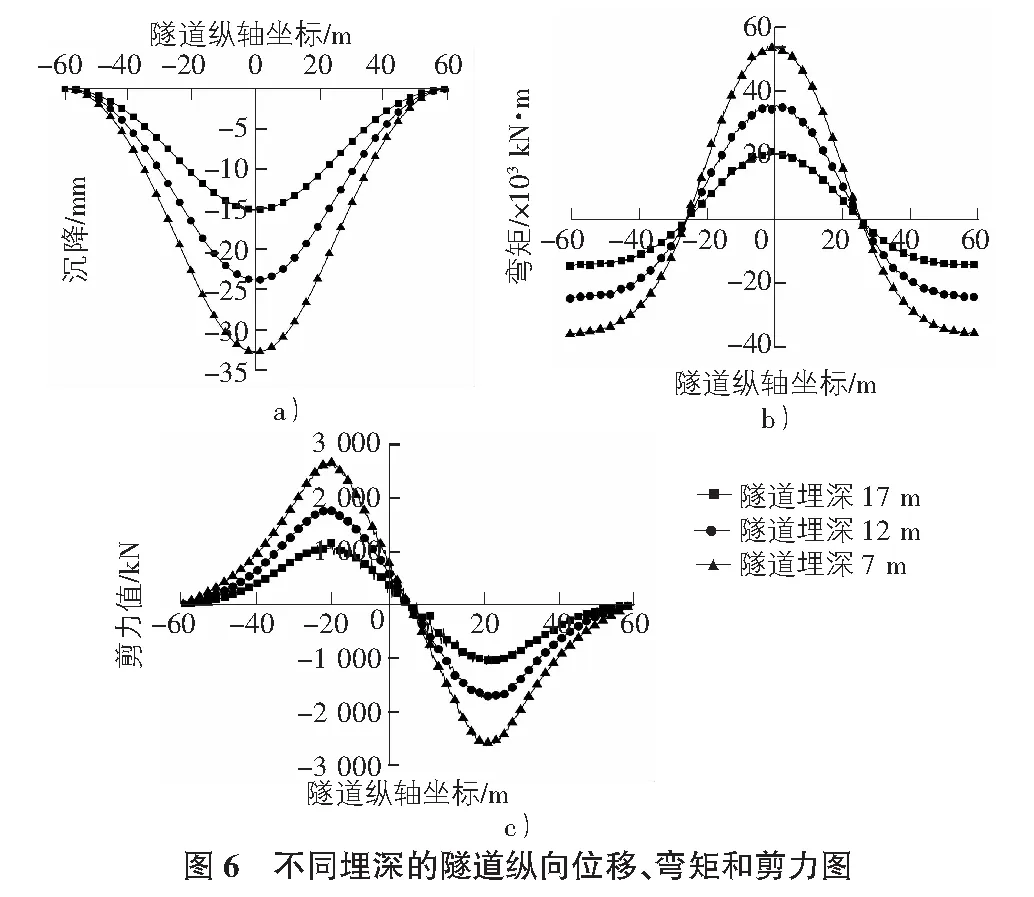
4.2 荷载位置对隧道变形的影响

如图7所示为荷载中心距离隧道中心为0 m，10 m，20 m时隧道纵向变形的模拟结果。结果显示，不同荷载位置隧道变形的规律一致，数值不一。距离越近，隧道变形越大。随着荷载位置距离轴中心位置越来越远，隧道最大沉降量、弯矩、剪力值逐渐减小，且减小的幅度逐渐增大。例如，对于隧道沉降量，荷载中心距轴0 m，10 m，20 m的最大沉降量分别为30 mm，23.7 mm，11.3 mm，减小的程度分别为21%，52%。因此，可以推测，荷载距离增大到一定程度后，对于深埋隧道的影响可以忽略。

5 结论与建议

目前新建盾构隧道大多采用深埋的方式，为了考虑周围土体的抗剪性能对盾构隧道结构的约束作用，本文基于改进的双面弹性地基梁模型，借助有限元软件分析了堆载引起的地铁隧道的纵向变形，并考查了不同埋深、不同堆载位置对于隧道纵向变形的影响，得出以下结论：

1)基于双面弹性地基梁模型，采用有限元软件计算隧道纵向变形得出的结果，规律与文献[9]中理论推导的结果一致，但是数值存在一定的差异。两者的结果都比基于温克尔弹性地基梁模型分析的结果更合理。

2)埋深越浅，隧道纵向最大沉降量、弯矩、剪力值越大。随着隧道埋深的增加，隧道的最大沉降量、弯矩、剪力值迅速减小。

3)荷载中心距离隧道中心的距离对于隧道纵向变形的影响会随着距离的逐渐增大而减弱。

[1] 林永国,廖少明,刘国彬.地铁隧道纵向变形影响因素的探讨[J].地下空间与工程学报,2000,20(4):264-267.

[2] 吴 庆,杜守继.地面堆载对既有盾构隧道结构影响的试验研究[J].地下空间与工程学报,2014,10(1):57-66.

[3] 戴宏伟,陈仁朋,陈云敏.地面新施工荷载对临近地铁隧道纵向变形的影响分析研究[J].岩土工程学报,2006,28(3):312-316.

[4] 廖少明.圆形隧道纵向剪切传递效应研究[D].上海：同济大学,2002.

[5] 臧小龙.软土盾构隧道纵向结构变形研究[D].上海：同济大学,2003.

[6] 林永国.地铁隧道纵向变形结构性能研究[D].上海：同济大学,2001.

[7] 张治国，张孟喜，王卫东.基坑开挖对临近地铁隧道影响的两阶段分析方法[J].岩土力学，2011，32(7)：2085-2092.

[8] 白海卫.新建隧道下穿施工对既有隧道纵向变形的影响和工程措施研究[D].北京：北京交通大学,2007.

[9] 璩继立,潘 荣,唐瑞东.基于双面弹性地基梁的隧道纵向变形研究[J].水资源与水工程学报,2016,27(1):190-194.

[10] GB 50307—1999，地下铁道、轻轨交通岩土工程勘察规范[S].

[11] [日]土木学会.隧道标准规范(盾构篇)及解说[M].朱伟,译.北京:中国建筑工业出版社,2001.

Finite element modelling of longitudinal deformation of tunnels based on the double elastic foundation beam

Ding Zhijun Liu Lvzhi Pan Rong

(UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The double elastic foundation beam model and the finite element software were used to analyze the longitudinal deformation of deep-lying shield tunnel by the heaped load. The effect of different depth and different load position on longitudinal deformation was also investigated. The results showed that the finite element method was feasible to analyze the longitudinal deformation of tunnel based on the elastic foundation beam model. Both the increase of the depth of the tunnel and the distance of the heaped load decreased the longitudinal deformation of the tunnel gradually.

the beam on double elastic foundation， deep-lying tunnel， finite element， longitudinal deformation

1009-6825(2017)03-0156-03

2016-11-16

丁志军(1990- )，男，在读硕士

U451

A