图形法在高中地理时间计算中的应用

●江西省赣州市赣县中学 邓少杨

图形法在高中地理时间计算中的应用

●江西省赣州市赣县中学 邓少杨

在高中地理教学过程当中，关于地球运动的部分是教学的重点之一，同时也是高中地理的教学难点，这一部分的知识既包含地球的公转，同时也包含地球的自转。可以说，这也是学生遇到的第一个难点。

在实际的教学过程中我们发现，关于这一部分的教学困扰着很多教师，而对于地球运动的学习也困扰了很多学生。很多教师都认为这是因为学生没有足够的思维能力，因此，在高中地理教学过程当中如何才能够提高学生的空间思维能力就显得异常重要。一般来讲，可以通过提高学生的抽象洛基思维能力或者是将抽象概念具体化两种方法来进行解决，本文采用了后一种方法，在实际的教学过程中取得了不错的效果。

一、在圆上解决时间计算

1.在圆上的时区划分。

在地理课程中第一次出现涉及时区问题是在初中阶段，如图1所示，这种插图类似于展开状的地图，其实就是将一条直线平均划分为24条线段，但是，这种插图很难让学生将时区、地球运动等联系起来的。大部分教师进行该内容的教学过程当中，都采用了相似的辅助图来进行教学，但是这种辅助图对于学生的思维能力有着较高的要求，因此很多学生都认为这一部分是学习地理的瓶颈。

考虑到地球上任意一点的时间只和纬度有关，我们可以将一条抽象的线首尾相连形成一个圆形，这样就可以在这个圆形当中解决与时间有关的问题。如图2所示。

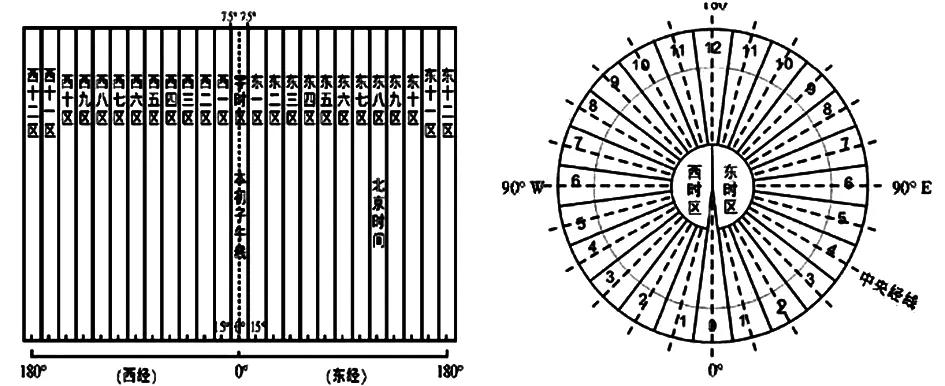
图1 直线型时区划分图 图2 圆形时区划分图

从图中我们可以看到，利用这种图示，我们清楚地明白了时区与区时的基础知识。例如，经度每隔15°为一个时区，全球24个时区；在中时区以东，每15°划为一个时区，分别是东一区到东十二区，中时区以西同理等。

而利用圆形时区划分图，我们能够轻松解决很多地球运动的问题。例如，在知道某一个地方的地方时的情况下，求出另一个地方的地方时；在知道某一个地方的经度以及时差的情况下，求另外一个地方的经度等。

2.在圆上的日期变更。

想要解决日期变更的问题，首先应该分清楚人为日界线以及自然日界线的概念。所谓的人为日期变更线也就是180°经线，这条线在地球上的位置是不会变动的，而自然日期变更线则是地方时为0时的经线，这条线在地球表面自东向西不停地进行移动。

在高中地理教学过程当中，我们经常利用图3来进行判断，该图与图1相似，对于学生的思维能力有着较高的要求，并不利于教学。

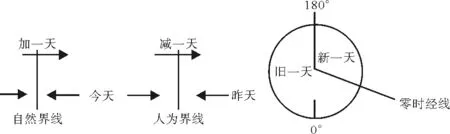
图3 直线型日期变更辅助图 图4 圆形日期变更辅助图

如果我们在圆上解决日期变更的问题，利用图4则可以更为直观地体现出来。

二、对地球运动部分教学建议

1.难点问题简单化。

在教学过程当中，教师应该寻找将问题简单化的方法，保证能够在学生抽象思维能力不强的情况下发挥学生的具象思维能力，从而完成教学难点的突破。

2.正确理解空间思维能力的培养。

不能否认的是，如果学生具有较强的空间思维能力，就能够更好地理解地球运动部分的教学内容，但培养学生的地理思维能力仍然是高中地理教学的目的之一。

在高中地理教学过程当中，教师应该寻找合适的教学方法，让学生能够更好地学习教学中的难点以及重点，培养学生的空间思维能力不应该以培养学生的抽象思维能力为主，而应该发挥学生的优势，利用地图将问题简单化处理，将抽象的知识具现出来，辅助学生进行解题。