透析错例 把握实质
汤建明

“平面图形的认识(二)”是初中数学中“图形与几何”的基础,在学习的过程中,常常会出现因不能正确理解基本概念、基本性质而导致的各种错误.现举例说明,望同学们在学习的过程中注重概念的了解、性质的理解,学会对数学本质的掌握.
一、不能正确理解平行线的性质
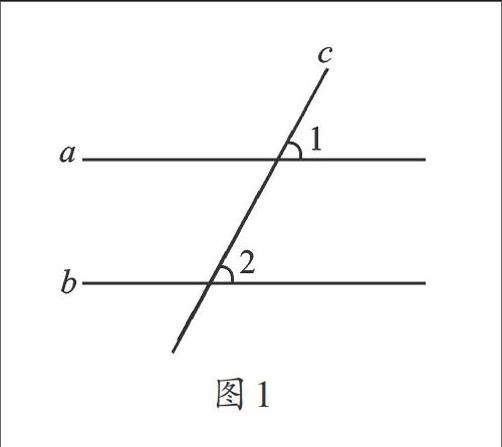
例1 如图1,直线c与直线a,b相交,若∠1=56°,则∠2等于( ).
A.34° B.56°
C.124° D.不能确定
【错解】B.
【分析】从图形来看,∠1、∠2是直线c被直线a、b所截后所得的两个同位角,误以为根据平行线的性质可得:∠1与∠2具有相等关系.平行线的性质“两直线平行,同位角相等”的条件是两直线平行,结论是同位角相等.本题中直线a,b的位置没有明确给出平行,因此,∠1与∠2是否具有相等关系也就不能确定.
【正解】D.
【警示】“两直线平行,同位角相等”“两直线平行,内错角相等”“两直线平行,同旁内角互补”这些平行线的性质,都是在两直线平行的条件下,两角之间具有的数量关系.
二、不能正确理解“三线”的概念
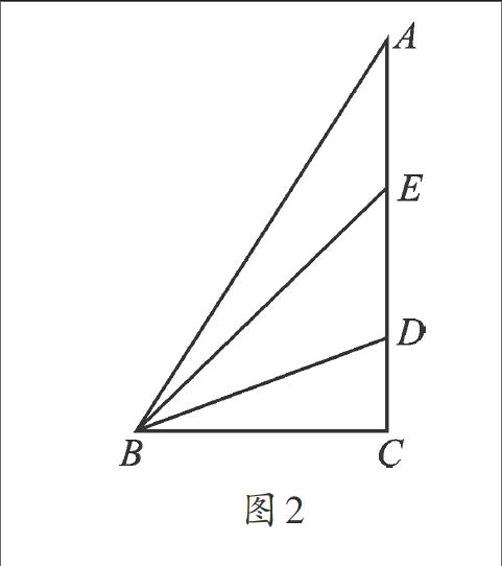
例2 如图2,在△ABC中,∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( ).
A.BC是△ABE的高
B.BE是△ABD的中线
C.BD是△EBC的角平分线
D.∠ABE=∠EBD=∠DBC
【错解】C.
【分析】根据条件“∠C=90°”即可知:BC⊥AC,垂足为点C,则BC可以看成是△ABC、△BEC、△BCD、△ABD、△BED以及△ABE的高,则选项A是正确的,不符合题意;根据条件“AE=DE”即可知:点E是△ABD的边AD的中点,即为△ABD的中线,则选项B是正确的,不符合题意;根据条件“BD平分∠EBC”即可知,BD是△EBC的角平分线,则选项C也是正确的,不符合题意;∵BD平分∠EBC,∴∠EBD=∠DBC.∵AE=DE,△ABD不是等腰三角形,∴∠ABE≠∠EBD,∴∠ABE=∠EBD=∠DBC不成立,则选项D是不正确的,符合题意.
【正解】D.
【警示】三角形的角平分线、高、中线是三角形重要的线段,熟记这些概念并正确识图是解答这类问题的关键.
三、没有掌握中线性质
例3 如图3,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且S△ABC=16cm2,则S阴影= cm2.
【错解】8.
【分析】由条件“点D、E、F分别为边BC、AD、CE的中点”可知:AD、BE、CE、BF分别为△ABC、△ABD、△ACD以及△BCE的中线,根据“等底等高的两个三角形面积相等”可得:S△BED=[12]S△ABD、S△ECD=[12]S△ACD,所以S△BEC=[12]S△ABC,同理可得S△BEF=[12]S△BEC,即S△BEF=[14]S△ABC
=4cm2.由于有的同学不能掌握中线性质,即三角形中线将三角形分成两个面积相等的三角形,而不能对这类图形的面积加以转化.
【正解】4.
【警示】根据等底等高的三角形的面积相等,可知道三角形的中线把三角形分成两个面积相等的三角形.解答这类问题时,我们要善于将这类不规则的图形逐步转化为熟悉的图形或可以求的图形面积问题.
四、不能正确理解三角形的三边关系
例4 (2016·淮安)已知一个等腰三角形的两边长分别为2和4,则该等腰三角形的周长是 .
【错解】10或8.
【分析】因为所给的等腰三角形的两边长分别为2和4,所以对这两边到底是这个等腰三角形的腰还是底边,需要分情况加以讨论.即:(1)三角形的三边长分别为2,2,4,∵2+2=4,∴它们不能构成三角形,即此种情况不存在;(2)三角形的三边长分别为2,4,4,此时能构成三角形,且周长为10.综上所述,该等腰三角形的周长为10.而有的同学仅仅考虑了等腰三角形边的情况,忽视了三角形的三边关系,即三条线段能否构成三角形,而出现错误的结论.
【正解】10.
【警示】解决与三角形三边长有关的问题时,一定要考虑构成三角形的三边长能否满足三角形的三边关系.
五、考虑问题不全面,不能正确分类讨论
例5 (2016·涼山)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( ).
A.7 B.7或8
C.8或9 D.7或8或9
【错解】B或C.
【分析】设内角和为1080°的多边形的边数是n,则(n-2)·180°=1080°,解得:n=8.即切去一个角后,形成的另一个多边形的边数为8.由于原多边形切去的这个角怎么切的没有说明,因此有三种可能出现的结果,即边数不变、边数增加1、边数减少1,则原多边形的边数为7或8或9.
【正解】D.
【警示】解答这类操作性问题时,先确定内角和为1080°的多边形边数,再根据操作过程中可能出现的结果进行分类讨论.
(作者单位:江苏省建湖县城南实验初中教育集团城南校区)

