一类分形方块(Σ3,7)的拓扑豪斯道夫维数

李青，代玉霞，柯枫

(湖北大学数学与统计学学院，湖北 武汉 430062)

一类分形方块(Σ3,7)的拓扑豪斯道夫维数

李青，代玉霞，柯枫

(湖北大学数学与统计学学院，湖北 武汉 430062)

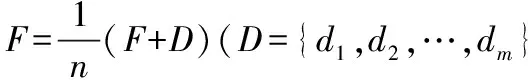
分形方块；拓扑基；拓扑豪斯道夫维数

0 引言及结果

设n≥2，记D={d1,d2,…,dm}⊆{0,1,…n-1}2为一个数字集，其中#D=m表示D的基数.

设

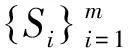
(1)

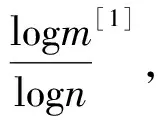
(2)

其中C≥1为常数. 文献[2-4]研究了分形方块的拓扑结构和李卜希兹等价类.

本文中主要研究分形方块的拓扑豪斯道夫维数，先回顾拓扑豪斯道夫维数的定义[5].

定义1.1 定义dimtHφ=-1.对非空度量空间X，定义X的拓扑豪斯道夫维数为

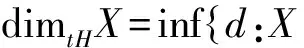
其中∂A表示集合A的边界，dimH表示豪斯道夫维数[1].

本文中dimt表示拓扑维数[6-7]. 下面性质给出了拓扑豪斯道夫维数与拓扑维数及豪斯道夫维数之间的大小关系.

性质1[5]对任意的度量空间X，有dimtX≤dimtHX≤dimHX.

下面性质说明了拓扑豪斯道夫维数的单调性.

性质2[5]对任意的度量空间X⊆Y,有dimtHX≤dimtHY.

下面性质是研究拓扑豪斯道夫维数的一个基本性质.

性质3[5]对任意的度量空间空间X,Y,若f:X→Y是一个满足(2)式的一个双射，则dimtHX=dimtHY.

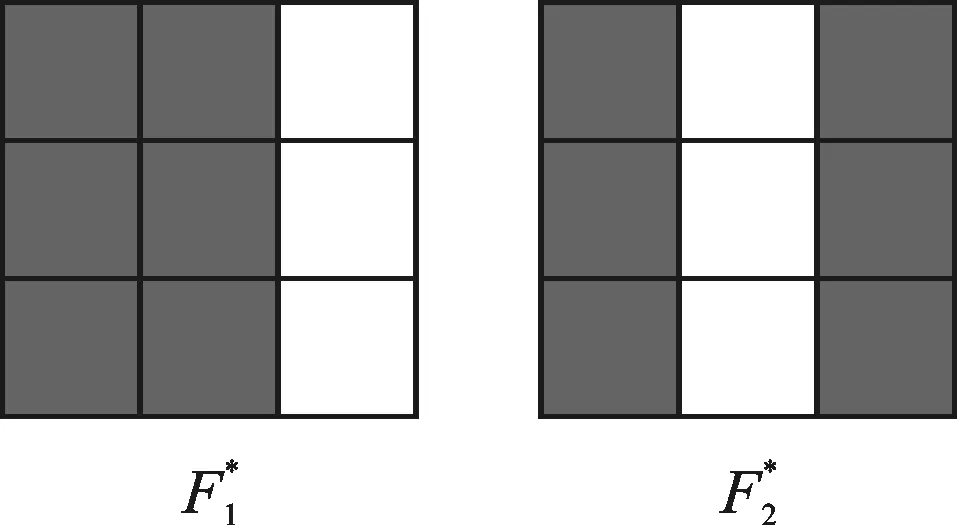
本文中主要研究Σ3,7中的分形方块的拓扑豪斯道夫维数.Σ3,7有如下8个分形方块.

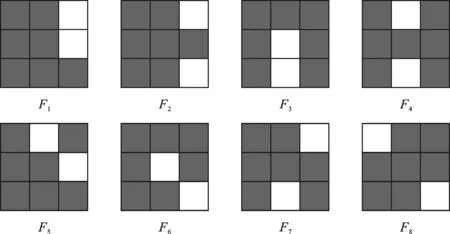
图1 Σ3,7中分形方块

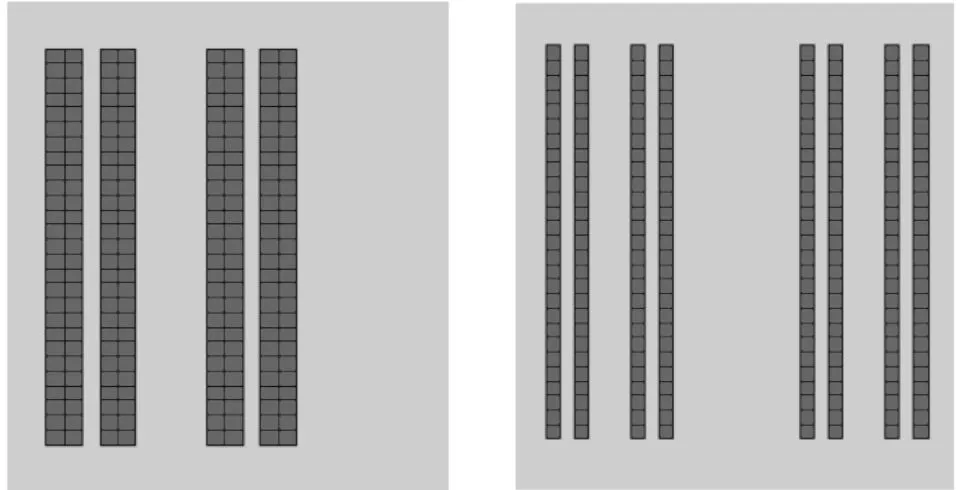
其经过多次迭代后如下图所示:

图2 Σ3,7中多次迭代后的分形方块

下面定理给出了本文中的主要结论.

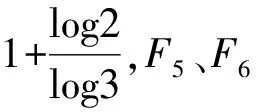
注释：对F7、F8的拓扑豪斯道夫只知其精确下界为1，未能得到其精确上界.

1 预备引理

为证明定理，本节介绍证明中用到的引理，主要是给出分形方块上拓扑基(后面简称基)的构造方法，先给出基的等价描述.

定理1.1[8]设Ц是拓扑空间(X,J)上的一个开集族，则Ц是拓扑空间的一个基当且仅当对于每一个x∈X和x的每一个领域Ux，存在Vx∈Ц使得x∈Vx⊆Ux.

下面引理给出了分形方块矩形基的一种构造方法.

引理1.2[9]设F是一个分形方块，E是[0,1]的稠密子集，记

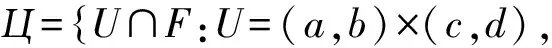
则Ц是F的一个基.

定理1.4[5]设X是一个非空的可分度量空间.则

dimtH(X×[0,1])=dimH(X×[0,1])=dimHX+1.

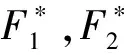
其经过多次迭代后的图形如下:

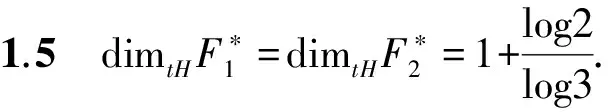
(3)

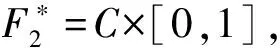
结合(3)式得证.

2 定理的证明

本节分3种情形证明定理.

情形一(构造引理1.3中的基)

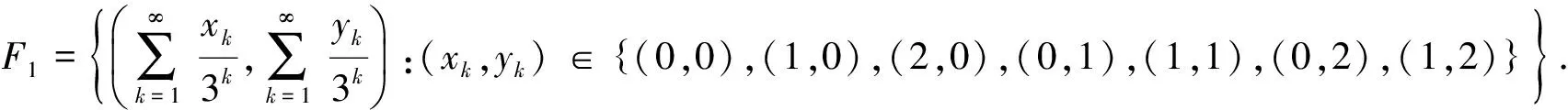
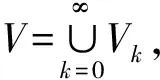
对任意p=(a,b)∈V，存在k≥0，使得x∈Vk+1Vk. 取p的关于直线y=b对称的邻域U1(p)满足

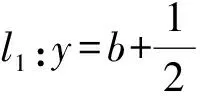
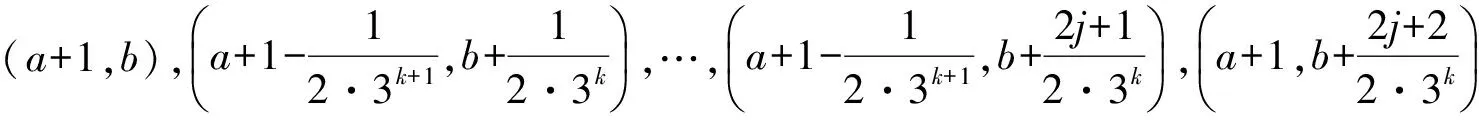
(iii)C1,2是C1,1向左平移2个单位所得.

递归作p的关于直线y=b对称的邻域Un(p)，n≥2满足

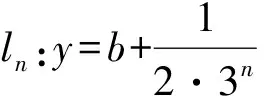
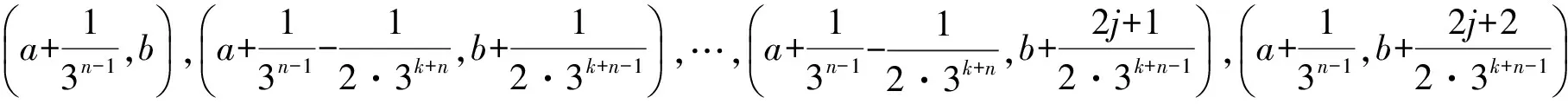
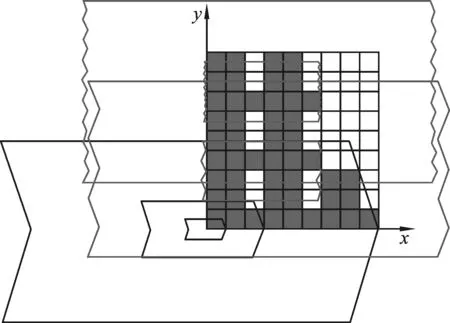
图3 F1的一个拓扑基

(iii)Cn,2是Cn,1向左平移2/3n-1个单位所得.

如图3所表示.

由上述构造可得，对任意p∈V，有Un+1(p)∈Un(p)且

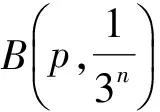
令

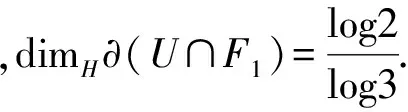
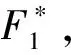
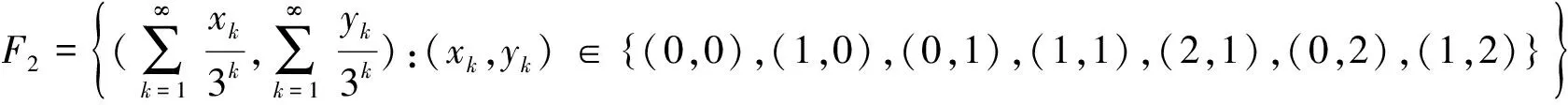
类似于F1中的方法，对于任意的p=(a,b)∈V(V同上)，作Un(p)满足

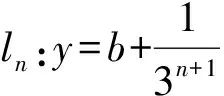
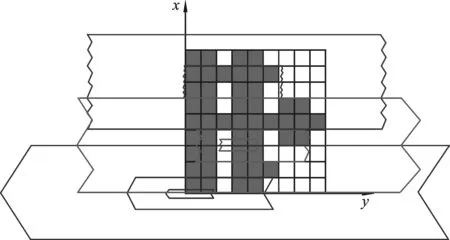
图4 F2的一个拓扑基

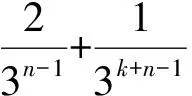
如图4所表示.

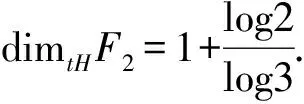
情形二(构造引理1.2 中的基)

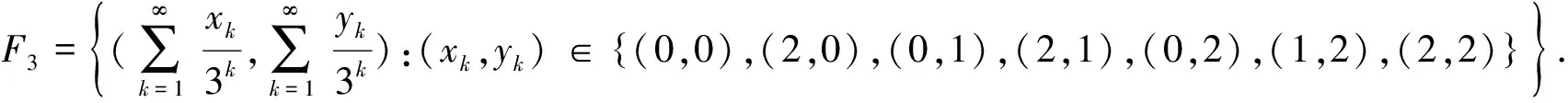
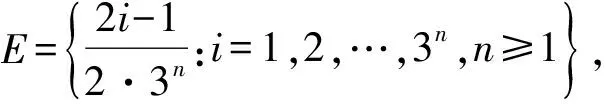
令

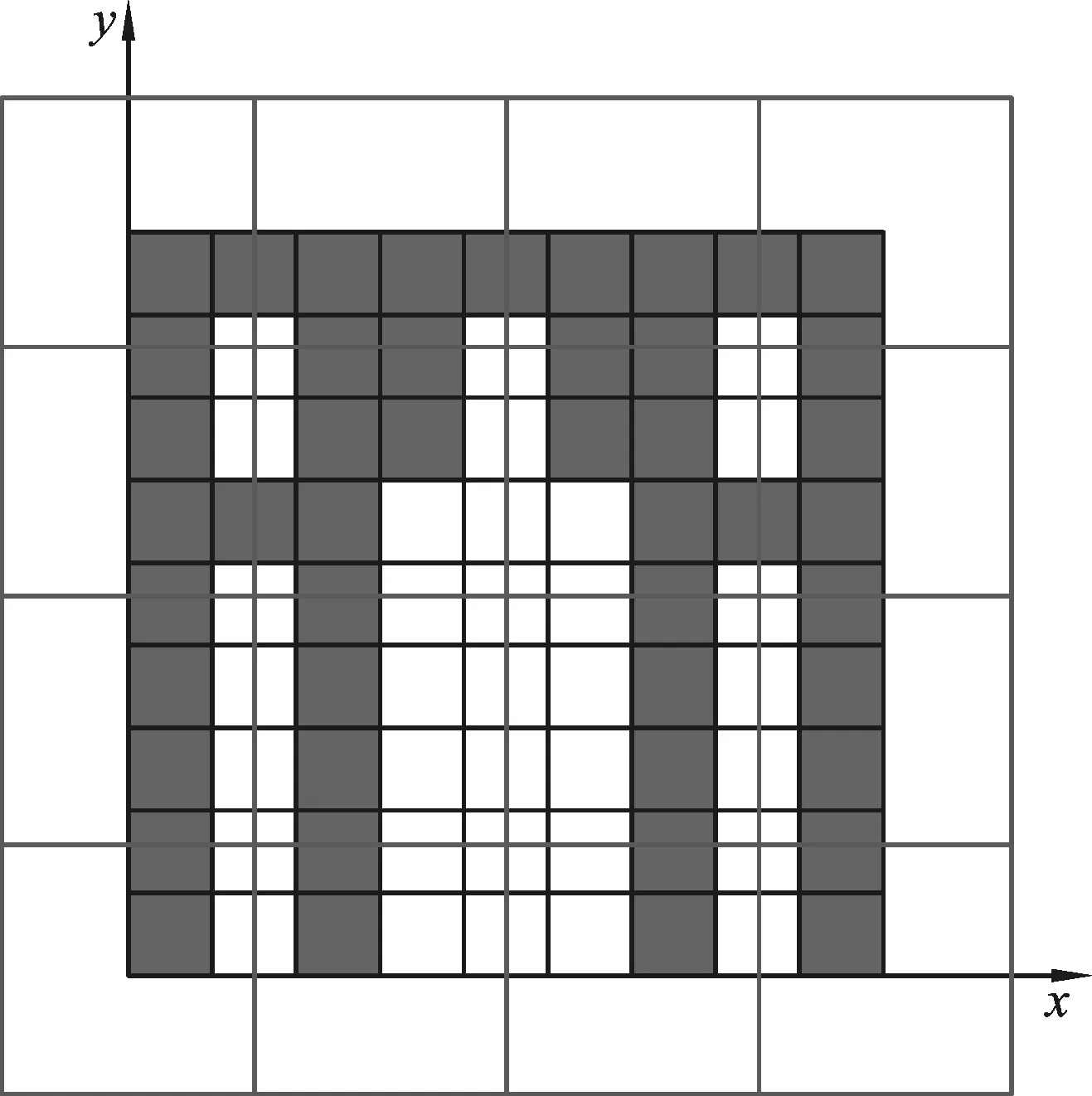
图5 F3的一个拓扑基

则任意的U∩F3∈Ц，U∩F3的顶点均属于E×E，从而由引理1.2，Ц是F3的基.

如图5所表示.

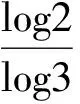
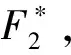
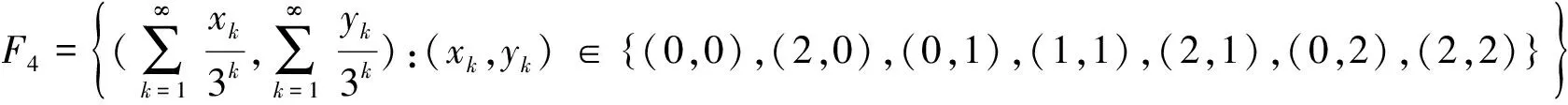
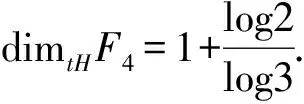
情形三

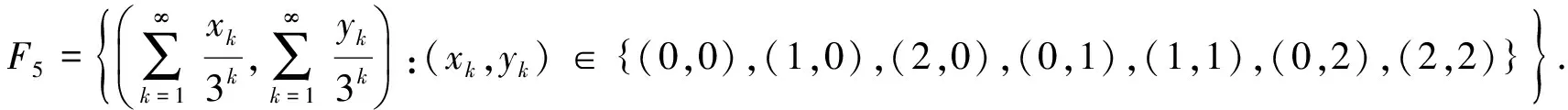
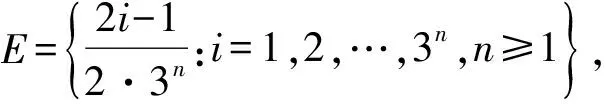
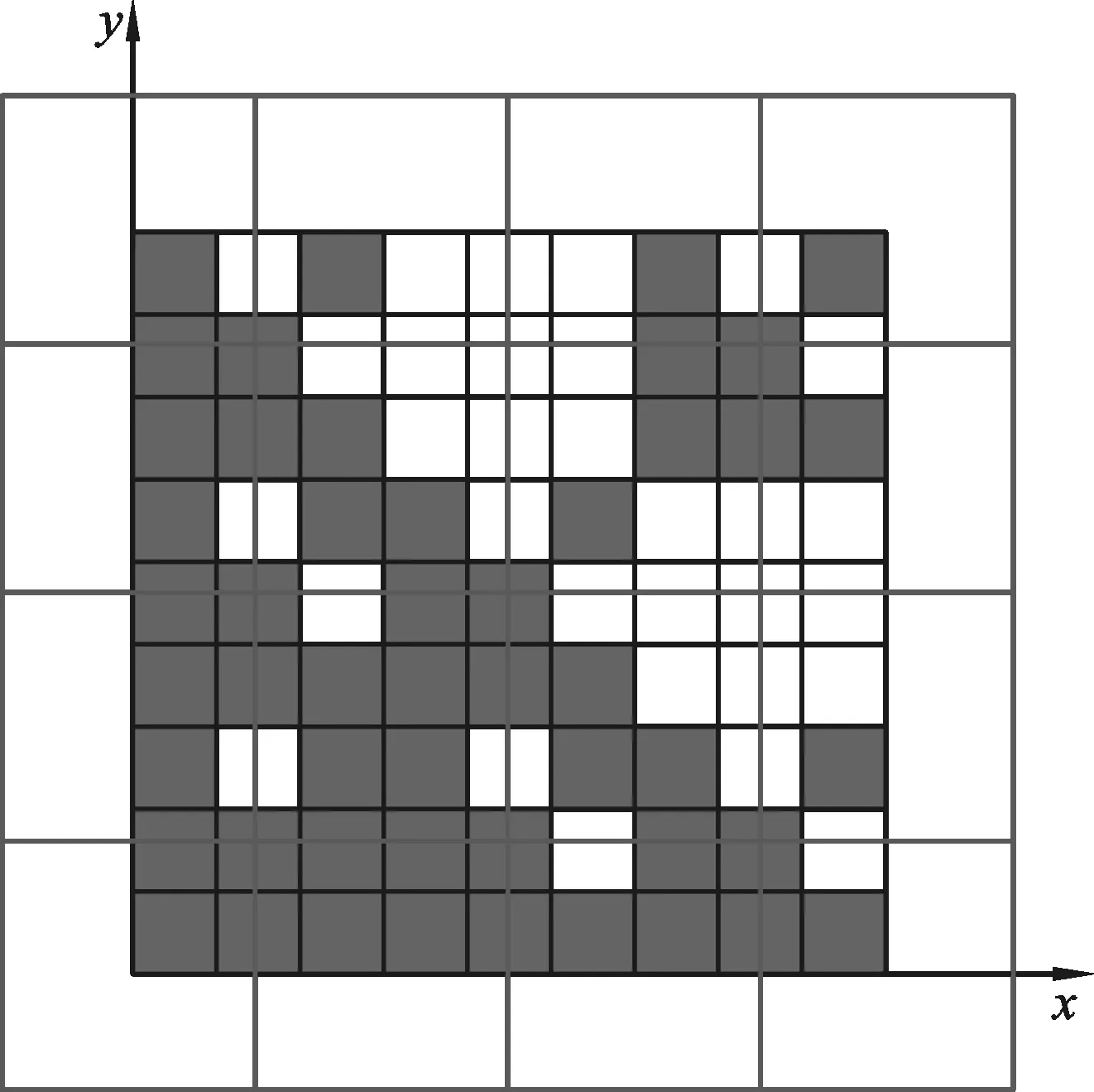
图6 F5的一个拓扑基

则任意的U∩F5∈Ц，U∩F5的顶点均属于E×E，从而由引理1.2，Ц是F5的基.

如图6所表示.

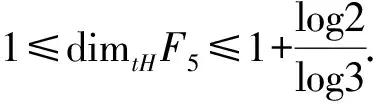
[1] Falconer K J. Fractal geometry-mathematical foundations and applications[J].Mathematical Fouundation and Applications, John Wiley, 1990.

[2] Lau K S, Luo J J,Rao H.Topological stucture of fractal squares[J].Math Proc Camb Phil Soc, 2013,155:73-86.

[3] Luo J J,Liu J C. On the classification of fractal squares[J].preprint.

[4] Zhu Y J, Rao H. Lipschitz equivalence of fractal aquares[J].preprint.

[5] Balka R,Buczolich Z, Elekes M.A new fractal dimension: The topological Hausdorff dimension[J].Advances in Mathwmatices. 2015,274:881-927.

[6] Heinonen J. Lectures on analysis on metric space[J], New York: Springer-Verlag,2001.

[7] Hurewicz W, Wallman H. Dimension Thorery[M].OSA princeton Uiversity Press,1948.

[8] 熊金成.点集拓扑讲义[M].北京：高等教育出版社，2011.

[9] 柯枫，代玉霞，李青. 一类分形方块的拓扑豪斯道夫维数[J].预出版.

(责任编辑 赵燕)

The topological Hausdorff dimension of a class of fractal squares

LI Qing, DAI Yuxia, KE Feng

(School of Mathematics and Statistics, Hubei University, Wuhan 430062,China)

fractal square; topological basic; topological Hausdorff dimension

2016-08-06

国家自然科学基金(11301162)资助

李青(1990-)，女，硕士生；代玉霞，通信作者，讲师，研究方向：分形几何，E-mail:daiyuxia8173@163.com

1000-2375(2017)02-0112-07

O211

A

10.3969/j.issn.1000-2375.2017.02.002