自由漂浮空间机器人视觉伺服系统研究
刘阳, 谢宗武, 王滨, 刘宏, 蔡鹤皋
(哈尔滨工业大学 机器人技术与系统国家重点实验室, 黑龙江 哈尔滨 150001)
自由漂浮空间机器人视觉伺服系统研究
刘阳, 谢宗武, 王滨, 刘宏, 蔡鹤皋
(哈尔滨工业大学 机器人技术与系统国家重点实验室, 黑龙江 哈尔滨 150001)
为了将动力学模块引入传统的视觉伺服控制算法,使其更加符合真实模型。本文以自由漂浮空间机器人视觉伺服为目标,分析了其系统组成与工作原理。采用广义雅克比的方法完成其速度级的运动学建模,并在6D 空间下分析其动力学模型。机械臂采用PD与前馈控制完成笛卡尔空间点到点连续路径规划。借助双目手眼相机完成非合作目标位姿的提取,进而完成视觉伺服系统的搭建。本文算法可将机械臂控制算法引入到空间机器人视觉伺服系统,使得机器人控制更加方便,具有结构简单成本低等优点。通过搭建SimMechanics仿真模型,实现了对期望轨迹的跟踪,验证了视觉伺服算法的正确性。
空间机器人;视觉伺服;自由漂浮;动力学;双目视觉
随着科学技术水平的发展,每年发射进入太空的航天器数目在逐渐增大。UCS(union of concerned scientists)卫星数据显示[1],截止到2016年1月1日,太空中活动卫星的数量为1 381,其中493颗卫星运行于同步地球轨道。这些活动卫星中大约有68%的卫星处于不受控状态,如废弃卫星、火箭残留物以及太空垃圾[2]。每年都有卫星由于发射失败而无法正确进入轨道,从而造成大量的经济损失。此类卫星经过在轨维护,大多可以继续服务。
作为主要的在轨维护设备,空间机器人能够胜任卫星维修、能源补充、货物运输等多项太空任务[3-8]。随着太空任务的复杂化,宇航员的操作风险大大提高,利用空间机器人代替宇航员完成空间工作已成为当前空间探索的新趋势。中国将在未来五年内建成我国独立自主研发的空间站,空间站各舱段之间的组装依赖的也是空间机器人。
空间机器人是一个强非线性系统,其运动学与动力学之间存在着动力学耦合[9]。空间微重力环境下对其进行实时控制存在很大困难,同时风险高、难度大。视觉伺服的引入使得空间机器人在执行空间任务时变得智能化,能够根据不同的环境采取不同的控制策略,从而能够胜任更为复杂与多种多样的空间任务。视觉伺服首先通过视觉信息获取机器人当前位姿与期望位姿的偏差,之后将其作为控制器的输入来规划各个关节的运动,进而实现对目标卫星的跟踪捕获任务。
研究自由漂浮空间机器人的视觉伺服系统既能使其具有感知空间环境的能力,同时也丰富了空间机器人系统建模方法。它能够有效的提高机械臂的控制性能,使其适应复杂多变的太空环境。根据相机数量的不同,视觉伺服可分为单目视觉伺服、双目视觉伺服与多目视觉伺服;根据相机安放位置的不同,视觉伺服可分为手眼相机系统与全局相机系统;根据偏差信号的选择,视觉伺服又可分为基于位置的视觉伺服、基于图像的视觉伺服及混合视觉伺服系统[10]。
本文以自由漂浮空间机器人视觉伺服为主要研究目标,选取基于位置的双目手眼视觉伺服系统,无需合作靶标即可实现对非合作目标卫星的位姿重建,同时回避了目标遮挡、图像雅克比奇异、相机回退等问题,控制器设计相对简单。假定图像处理模块能够精确获取目标位姿信息,本文研究了自由漂浮空间机器人视觉伺服系统的组成,详细分析了其进行运动学与动力学建模。通过在基于位置的传统视觉伺服算法的基础上添加空间机器人动力学模块,建立了自由漂浮空间机器人视觉伺服闭环系统。
1 空间机器人模型
自由漂浮空间机器人的一般模型如图1所示,整个系统可视为由卫星基座及n自由度机械臂组成。
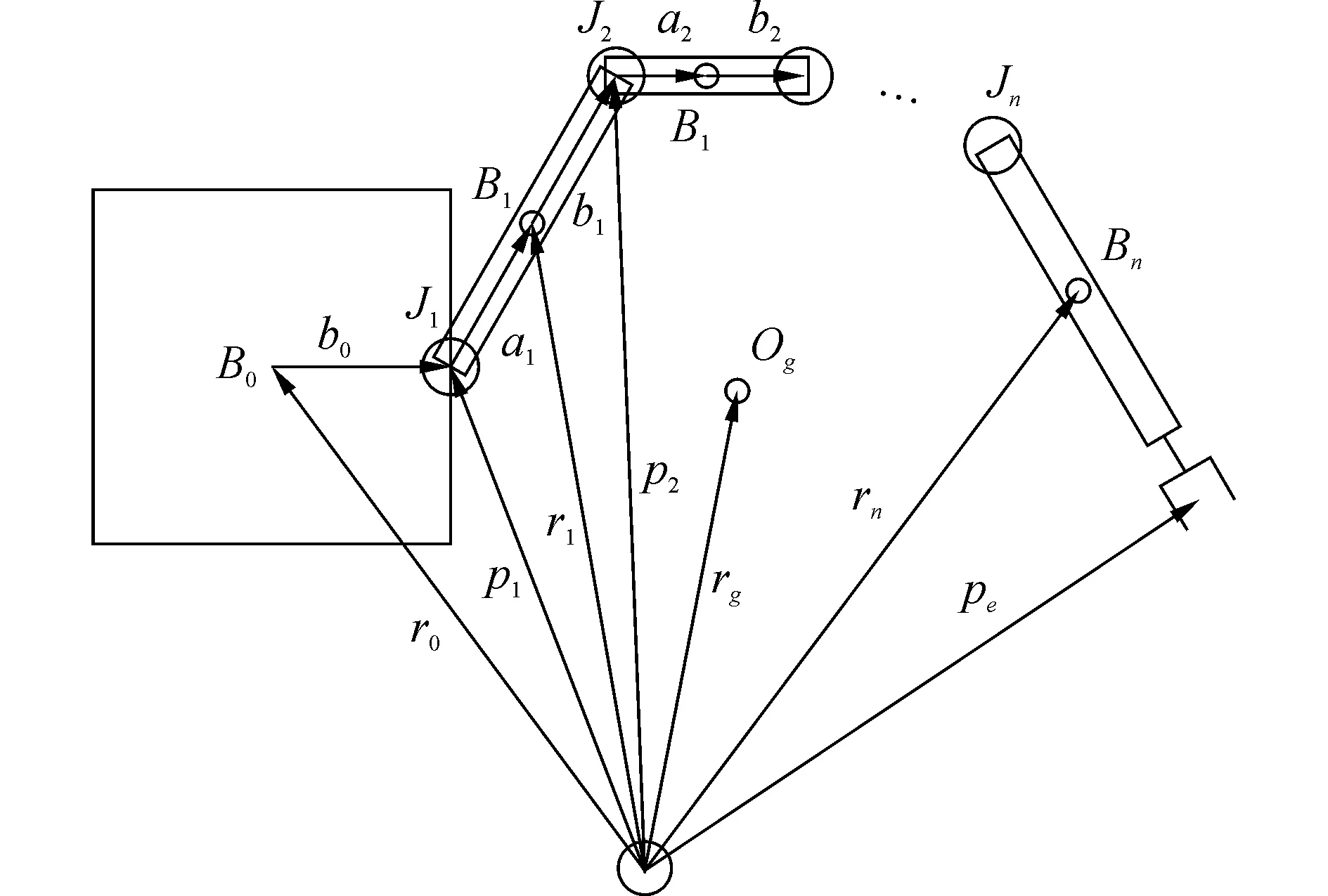
注:B0为空间机器人的卫星基座,Ji为关节i,ri∈R3为连杆i的质心位置矢量,pi∈R3为Ji的位置矢量,pe∈R3为机械臂末端的位置矢量,ai∈R3为第i个机械臂连体系与其质心系的相对位置矢量,bi∈R3为第i个机械臂质心系至第i+1个机械臂连体系的相对位置矢量图1 空间机器人模型Fig.1 The general model of space robot
本文所研究的空间机器人虚拟样机模型如图2所示,采用后置DH坐标系对其进行建模分析,各坐标系方向如图中所示,初始状态下机械臂对应的DH参数表如表1所示。

图2 空间机器人虚拟样机模型Fig.2 Virtual prototyping of space robot

连杆iθi/(°)di/mmai-1/mmαi-1/(°)1000-902-45080003000-9040600090522500906010000
为分析方便,本文对空间机器人的相关动力学参数作理想化处理,同时假设初始状态下,惯性系与基座系重合。
2 运动学建模
自由漂浮空间机器人的末端位姿受关节角与基座姿态的共同影响。非完整约束特性又使得基座的姿态与关节角的运动历史相关,故对于自由漂浮空间机器人,无法通过解析法得到位置级的运动学方程。下面将分别从正、逆运动学两方面对自由漂浮空间机器人进行运动学建模。
2.1 正向运动学建模
正向运动学是指已知空间机器人相关参数及关节角速度,求解机械臂末端的速度参数。本文采用Whitney矢量积法完成正向运动学建模[11]。
自由漂浮空间机器人的正向运动学方程可表示为
(1)
式中:
在自由漂浮状态下,空间机器人系统的线动量与角动量守恒。考虑整个系统相对于其本体质心的角动量,并假设其初值均为零,能够得到:
(2)
从而基座速度与关节角速度之间存在以下变换关系:
(3)
将式(3)代入式(1),从而得到自由漂浮模式下的空间机器人正向运动学方程:
(4)

2.2 逆向运动学建模
逆向运动学是指将空间机器人相关速度参数由笛卡尔空间转换至关节空间,本文通过对广义雅克比矩阵求伪逆来计算其逆运动学。
由2.1节可知:
(5)
广义雅可比矩阵Jg(Ψ0,Θ,mi,Ii)为6×n维矩阵。当n≠6时,无法直接对该矩阵求逆。考虑动力学奇异现象,对该矩阵的求逆操作变得更加复杂。
针对以上问题,本文首先对矩阵Jg进行奇异值分解:
Jg=UDVT
(6)
式中:U∈Rm×m、V∈Rn×n为正交矩阵,D∈Rm×n是以Jg的奇异值σ从大到小排列的对角矩阵,则广义雅克比矩阵伪逆的表达式为
(7)
式中:
此时空间机器人逆运动学方程可表示为
(8)
当σi接近于0时,计算得到的关节角速度容易超限。针对该现象,定义广义雅可比矩阵的阻尼最小方差逆:
(9)
式中:λ为阻尼系数,用来协调末端跟踪精度及关节角速度。为减小末端跟踪误差,当机械臂远离奇异构形时,应减小相应的阻尼系数。则自由漂浮空间机器人逆向运动学方程如下:
(10)
3 动力学建模
空间机器人动力学建模是其仿真实验、路径规划的基础。自由漂浮空间机器人处于失重状态,是典型的无根树系统。本文采用铰接体算法完成自由漂浮空间机器人的动力学建模[12]。
铰接体是指具有相对运动的刚体通过铰链组成的组合体。通过引入了6D空间矢量,铰接体算法将牛顿方程和欧拉方程结合到一起,既使得动力学方程变得简洁、直观,也提高了编程效率。
3.1 正向动力学建模
通过添加一个与惯性系相连的6自由度的虚拟铰链,可将自由漂浮空间机器人等效为一个固定基座机械臂。
自由漂浮空间机器人以基座为初始端的铰接体不受外力,则有下式成立:
(11)
进而求得卫星基座的加速度参数,由基座至末端机械臂逐步递推,即可求得各关节的角加速度,算法流程图如图3所示。

图3 铰接体算法流程图Fig.3 The flow chart of articulated-body algorithm
算法可分为以下三部分,6D空间矢量的引入使得方程表达式更为简洁,同时利用四元数来表示空间机器人基座的位姿参数以避免欧拉角奇异问题。
1)运动学外推。
由基座至末端逐步计算空间机器人各关节的速度与偏向力:
2)动力学内推。
由末端至基座逐步计算空间机器人各臂杆的惯量矩阵与铰接体偏向力:
3)角加速度外推。
由基座至末端逐步计算空间机器人卫星基座的加速度与各关节的角加速度:
3.2 逆向动力学建模
逆向动力学建模是指已知机器人各关节的角加速度,求解关节力矩的方法。本文自由漂浮空间机器人逆向动力学建模采用的是牛顿-欧拉递推算法,该算法是单处理器上计算效率最高的算法,其算法流程图如图4所示。

图4 牛顿-欧拉算法流程图Fig.4 The flow chart of Newton-Euler algorithm
算法可分为以下三部分:
1)运动学外推
由基座至末端逐步计算空间机器人各关节的速度、加速度与偏向力。
2)动力学内推
由末端至基座逐步计算空间机器人各杆件的惯量矩阵与铰接体偏向力。
3)关节力矩外推
由基座至末端逐步计算空间机器人卫星基座的加速度与各关节的关节力矩。
4 空间机器人路径规划
本文主要研究基于逆运动学的空间机器人笛卡尔空间点到点直线路径规划。根据计算方向的不同,机器人路径规划可分为基于正运动的路径规划与基于逆运动学的路径规划。基于正运动学的路径规划首先利用多项式函数对关节轨迹进行拟合,之后通过正运动学得到关于末端轨迹的非线性方程组,进而采用牛顿迭代法、遗传算法及粒子群算法等方法完成对关节轨迹的求解。基于逆运动学的路径规划算法通过求解机械臂末端速度,借助逆运动学直接求解得到关节角速度,具有计算量小、效率高等优点,可用于实时计算。
首先假设机械臂末端初始指向偏差为
(12)
式中:nt、ot、at为旋转矩阵表示的末端姿态。
同时假设空间机器人机械臂末端位姿轨迹:
(13)
两端微分后得到末端速度表达式:
(14)
联立式(10),则规划后的关节角速度曲线为
(15)
5 关节控制器设计
在机械臂处于低速运动时,可忽略离心力、科氏力以及臂杆间的耦合力矩的影响,将空间机器人系统近似视为解耦的线性系统,此时可采用基于n个独立关节的PD控制。而当各关节速度加快时,由于补偿效果变差,独立关节的PD控制的稳定性也变差。本文采用PD与前馈控制来设计关节控制器,前馈项由逆向动力学计算得到,其控制率如下:
(16)
式中:kip表示比例增益,它能够提高系统的稳态精度,但同时会增大系统的震荡次数。kid表示微分增益,它能够减小系统的超调及调节时间,实现超前控制,但同时系统的动态性能变差。τid表示由逆动力学算法计算得到的各关节期望力矩。
PD与前馈控制框图如图5所示,基于空间机器人模型的计算力矩模块独立于伺服回路之外,能够以较低速率运行,回路内部只需计算偏差信号带来的增益,计算量小,能以较高的伺服速率运行。

图5 PD与前馈控制框图Fig.5 The PD and feedforward control
6 自由漂浮空间机器人视觉伺服系统
自由漂浮空间机器人视觉伺服系统的组成,其流程图如图6所示。

图6 视觉伺服系统流程图Fig.6 The visual servo system of space robot
各组成模块分别实现以下功能:
1)成像系统。
双目手眼相机实时采集非合作目标图像,利用标定好的双目相机参数完成对双目图像的立体校正,使其满足对极几何的要求。经过立体校正,图像立体匹配时将由全平面的二维搜索变为沿极线方向的一维搜索,降低了计算量。
2)特征提取。
首先利用卫星喷管特征实现对非合作目标的粗定位,进而提取卫星基座边缘的角点特征。为了计算非合作目标的相对位姿,应至少提取3组对应的角点特征。经过特征提取,图像间的立体匹配变为了若干个像素点的匹配问题,大大减少了特征匹配时间,使得视觉伺服算法符合空间机器人实时控制的要求。
3)立体重建。
对特征提取得到的角点进行立体匹配,获取相应的视差数据。根据三角测距原理,借助重投影矩阵完成特征点的三维坐标计算。非共线的3个空间点将确定唯一的图像平面,进而求解卫星基座位姿。
4)PBVS控制器。
以上模块借助双目手眼相机完成了对非合作目标位姿的提取,从而可将其视为一个视觉位姿传感器,能够实时提供关于非合作目标卫星的当前位姿数据。PBVS控制器结合目标的期望位姿与当前位姿规划空间机器人机械臂末端的运动,输出期望的末端速度。
5)逆向运动学。
采用阻尼最小方差二乘法求解广义雅克比矩阵的伪逆,进而将速度由笛卡尔空间转换至关节空间,积分后得到相应的关节角。
6)关节控制器。
关节控制器采用PD与前馈控制算法。经由逆向动力学模块计算期望的关节力矩,并将其作为控制器的前馈项。同时利用关节传感器采集当前的关节角及角速度,对其采取PD控制,输出实际的关节力矩。
7)正向动力学。
采用铰接体算法计算实际的关节角加速度,积分后得到实际的关节角度与角速度。
8)正向运动学。
采用基于Whitney矢量积法的正向运动学求解自由漂浮空间机器人机械臂末端的实际速度,积分后得到当前位姿。
整个视觉伺服过程可等效为惯性系下由目标当前位姿到期望位姿的笛卡尔空间点到点的连续路径规划,其中当前位姿由双目手眼相机计算得到。下面,将通过如图7所示的SimMechanics仿真模型来验证本文提出的自由漂浮空间机器人视觉伺服算法的有效性。SimMechanics是机器人建模过程中常用的仿真工具,通过搭建与系统等效的模块框图,使机器人的系统建模变得更加方便直观。

图7 空间机器人SimMechanics仿真模型Fig.7 The SimMechanics model of space robot


表2 视觉伺服系统参数表


图8 空间机器人各关节角度跟踪曲线Fig.8 Comparison in attitude angle of space robot
7 结论
本文主要研究了自由漂浮空间机器人视觉伺服系统的组成。采用PD与前馈控制分析了其笛卡尔空间的点到点连续路径规划,通过搭建SimMechanics仿真模型,验证了本文算法的正确性。
1)本文提供了一种通用的自由漂浮空间机器人建模方法,但未考虑实际环境下视觉算法时延的影响;
2)在传统的基于位置的视觉伺服算法的基础上添加空间机器人动力学模块,更贴合实际模型;
3)通过调整关节控制器,还可将各种机器人控制算法引入视觉伺服过程中去,具有结构简单、算法灵活、成本低等优点。
此外,本文仅以点到点的路径规划为例分析了闭环系统的组成,后续工作中应分析不同路径规划以及机械臂奇异构型时对视觉伺服系统带来的影响,进一步扩展其实际应用价值。
[1]XU Wenfu, LIANG Bin, LI Bing, et al. A universal on-orbit servicing system used in the geostationary orbit[J]. Advances in space research, 2011, 48(1): 95-119.
[2]CHEN Long, GUO Baolong, SUN Wei. Relative pose measurement algorithm of non-cooperative target based on stereo vision and RANSAC[J]. International journal of soft computing and software engineering, 2012, 2(4): 26-35.
[3]刘业超. 柔性关节机械臂控制策略的研究[D]. 哈尔滨: 哈尔滨工业大学, 2009: 3-13. LIU Yechao. Research on the control strategy for the flexible-joint robot arm[D]. Harbin: Harbin Institute of Technology, 2009: 3-13.
[4]刘阳. 面向非合作目标的空间机器人双目视觉伺服研究[D]. 哈尔滨: 哈尔滨工业大学, 2015: 1-7. LIU Yang. Binocular vision system of space robot for non-cooperative target[D]. Harbin: Harbin Institute of Technology, 2015: 1-7.
[5]DUBOWSKY S, PAPADOPOULOS E. The kinematics, dynamics, and control of free-flying and free-floating space robotic systems[J]. IEEE transactions on robotics and automation, 1993, 9(5): 531-543.
[6]VAFA Z, DUBOWSKY S. The kinematics and dynamics of space manipulators: the virtual manipulator approach[J]. International journal of robotics research, 1990, 9(4): 3-21.
[7]陈治科, 熊伟, 刘德生, 等. 在轨操作技术及国外发展分析[J]. 装备学院学报, 2014, 25(6): 63-68. CHEN Zhike, XIONG Wei, LIU Desheng, et al. Analysis of on-orbit manipulation technology and its overseas development[J]. Journal of equipment academy, 2014, 25(6): 63-68.
[8]梁斌, 刘良栋, 李庚田, 等. 空间机器人的动力学等价机械臂[J]. 自动化学报, 1998, 24(6): 761-767. LIANG Bin, LIU Liangdong, LI Gengtian, et al. Dynamically equivalent manipulator for a space manipulator[J]. Acta automatica sinica, 1998, 24(6): 761-767.
[9]ZHANG Yu, SUN Kui, LIU Hong, et al. Pose measurement of nozzle based on laser range finders for capturing satellite[J]. Proceedings of the institution of mechanical engineers, 2016, 230(8): 1385-1396.
[10]蔡勇. 弧焊机器人焊缝跟踪系统与位移运动学研究[D]. 西安: 西安理工大学, 2007: 8-10. CAI Yong. Welding seams tracing system on robot and its kinematics research[D]. Xi'an: Xi'an University of Technology, 2007: 8-10.
[11]曾岑. 在轨服务空间机械臂运动及任务规划方法研究[D]. 大连: 大连理工大学, 2013: 33-38. CENG Cen. Research on motion and mission planning methods for on-orbit servicing space manipulator[D]. Dalian: Dalian University of Technology, 2013: 33-38.
[12]FEATHERSTONE R, ORIN D. Robot dynamics: equations and algorithms[C]//Proceedings of 2000 IEEE International Conference on Robotics and Automation. San Francisco, CA: IEEE, 2000, 1: 826-834.
Research on the visual servo system of a free-floating space robot
LIU Yang,XIE Zongwu,WANG Bin,LIU Hong,CAI Hegao
(State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China)
In order to add the dynamic model of the space robot to the traditional visual servo algorithm and enhance the authenticity of the simulation system, this paper analyzes the composition and principle of a free-floating space robot, focusing on its visual servo system. Generalized Jacobian matrix was used to complete kinematic model of the free-floating space robot, and the dynamics model was discussed under the condition of 6D spatial vector. Based on PD and feedforward control, the path planning of the robot was programmed in Cartesian space. A binocular hand-eye camera system was built to extract the pose of the non-cooperative satellite which further used to complete the visual servo system. Various robot control algorithms can be introduced to the visual servo system that makes it more convenient and takes advantage of simple mechanism with low cost. By building a SimMechanics model, the expected trajectory had been tracked successfully which proved the visual servo system right.
space robot; visual servo; free-floating; dynamics; binocular vision
2016-05-09.
日期: 2016-11-16.
国家重点基础研究发展计划(2013CB733105).
刘阳(1990-), 男, 博士研究生; 谢宗武(1973-), 男, 教授,博士生导师; 王滨(1973-), 男, 副教授; 刘宏(1966-),男,教授,博士生导师,“长江学者计划”特聘教授; 蔡鹤皋(1934-), 男, 教授,博士生导师,中国工程院院士.
王滨,E-mail:wbhit@hit.edu.cn.
10.11990/jheu.201605027
http://www.cnki.net/kcms/detail/23.1390.u.20161116.1613.002.html
TP242.3
A
1006-7043(2017)02-0153-07
刘阳, 谢宗武, 王滨, 等. 自由漂浮空间机器人视觉伺服系统研究[J]. 哈尔滨工程大学学报, 2017, 38(2): 153-159. LIU Yang,XIE Zongwu,WANG Bin, et al. Research on the visual servo system of a free-floating space robot[J]. Journal of Harbin Engineering University, 2017, 38(2): 153-159.

