Weibull函数在杉木人工林直径分布中的研究

陈晨+刘光武

摘要：用Weibull 分布模型拟合林分直径分布，用最大似然估计法求其模型参数，再求出各径阶的理论株数值，并进行了x2检验，拟合精度达到84.91。研究结果表明：Weibull分布能较好地模拟林分直径分布。

关键词：杉木；人工林；Weibull函数；直径分布

中圖分类号：S791.28文献标识码：A文章编号：16749944（2017）03005902

1引言

林分直径分布是指在林分内各种大小直径林木按径阶分配的状态，它是基本的林分结构[1]。林分直径分布影响树高、干形、材积、材种及树冠等因子的变化，同时，研究林分直径分布规律对森林经营技术、编制经营数表、预估林分生长与收获模型及林分调查都有十分重要的意义。目前，关于林分直径分布规律的研究有很多，但普遍都是针对油松[2，3]、落叶松[4，5]、马尾松[6，7]等树种的，而对杉木的研究还很少。

在拟合直径分布时常根据直径分布的具体形态特征和变化规律，选用不同的概率分布函数，常用的分布函数有正态分布、对数正太分布、Sb分布等，本研究用Weibull函数来拟合杉木人工林的直径分布。

2材料与方法

2.1材料来源

供研究的材料来源于河南省信阳市鸡公山自然保护区某固定标准地，该保护区位于豫鄂两省交界处，面积287 km2，同时也是我国淮河与长江两大水系的分水岭，中国南北气候的分界线，北亚热带和暖温带的过渡地带。特殊的地理位置与气候特征，造就了此地的生物多样性。

2.2数据筛选

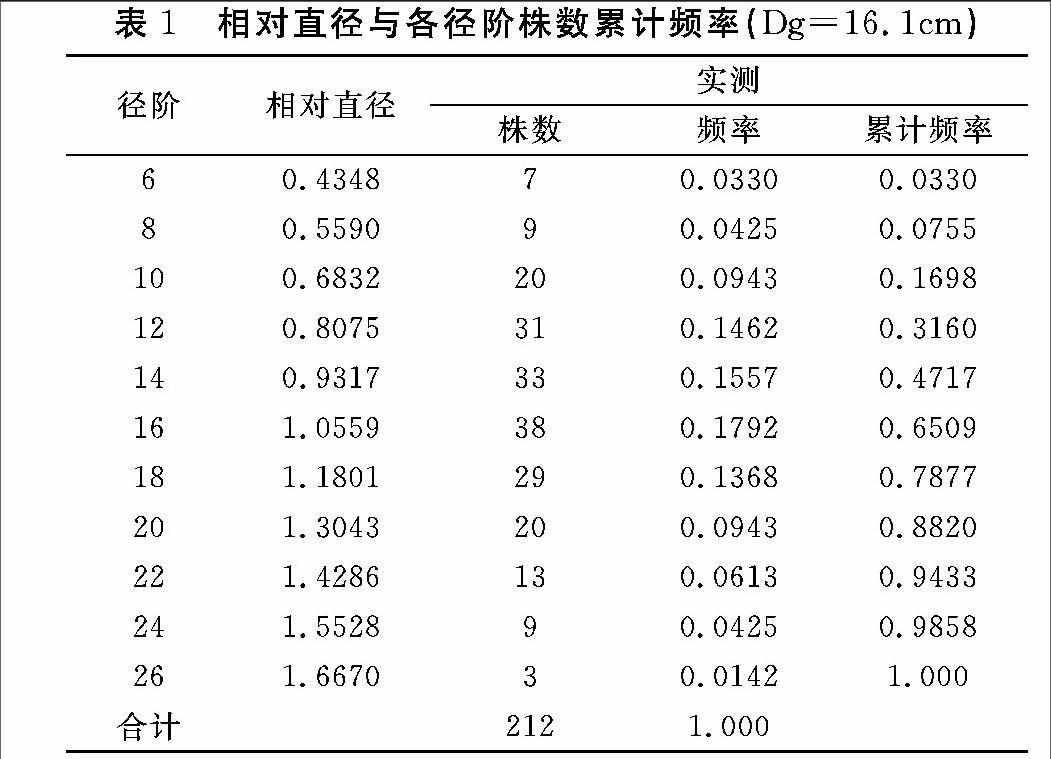
研究结果表明，不论树种、年龄、密度和立地条件如何，其林分平均直径（Dg）在株数累计分布曲线上的位置大致在55%～64%，一般在60%处[1]。从表1所示资料可以得出，相对直径等于1.0（即林分平均直径）所对应的株数累计百分数在57.0%处，说明所用固定标准地林分未遭受重大自然灾害、病虫害或人工抚育破坏，样本数据符合人工林直径分布规律，可以用来建立模型。

2.3研究方法

笔者用Weibull分布模型拟合林分直径分布。Weibull分布的密度函为：

式中：a为位置参数；b为尺度参数；c为形状参数，x为径阶中值。参数a一般定为林分直径最小径阶的下限值，b和c的求解以最大似然估计法最精确。这样，根据最大似然原理得到：

[∑ki=1fi·xci·In（xi）/（∑ki=1fi·xci）]-1c=1n[∑ki=1fi·In（xi）]（2）

b=[1n（∑1nfi·xci）1/c]（3）

式中：n=∑kifi；k为径阶个数；xi为第i径阶中值；fi为第i径阶内林木株数；n为总株数。

利用最大似然估计法求出三参数a、b、c的值之后，再利用下式求出标准地林木直径的Weibull分布各径阶的理论株数值，并进行X2检验。

ni=N·W·（ab）（xi-ab）c-1exp[-（xi-ab）c]（4）

式中：ni为第i径阶内理论株数值；N为林木总株数；W为径阶距；xi为第i径阶中值，其它符号同前。

3拟合结果

由表2可知， Weibull分布模型的拟合精度为84.91%，这说明Weibull函数具有较好的拟合效果，能4结论

用鸡公山林场固定标准地直径分布数据为研究材料，利用Weibull分布函数建立模型，再求出标准地林木直径的Weibull分布各径阶的理论株数值，并进行了x2检验。拟合精度达到84.91，研究证明Weibull分布模型在拟合林分直径分布时，灵活性高、适应性强，能较好地拟合实直径分布。

参考文献：

[1]孟宪宇.测树学（第二版）[M].北京：中国林业出版社，1996：66～98.

[2]刁军，雷相东，国红，等.北京西山油松人工林结构特征研究[J].河北林果研究，2009，24（3）：225～230.

[3]罗瑞平，亢新刚.黄龙山林区天然油松林直径结构规律[J].林业调查规划，2006，31（3）：86～88.

[4]王方，郑小贤，蒋桂娟.不同密度落叶松人工林直径结构研究[J].内蒙古林业调查设计，2011，34（5）：9～11.

[5]王香春，张秋良，春兰，等.大青山落叶松人工林直径分布规律的研究[J].山东农业大学学报（自然科学版），2011，42（3）：349～355.

[6]黄家荣，孟宪宇，关毓秀.马尾松人工林直径分布神经网络模型研究[J].北京林业大学学报，2006，28（1）：28～31.

[7]黄庆丰.马尾松林分直径结构规律的研究[J].安徽农业大学学报，1998，25（1）：23～25.

收稿日期：20170111

作者简介：赖宝乾（1964—），男，工程师，主要从事森林资源调查规划设计技术研究。2017年2月Journal of Green Science and Technology第3期