圆筒径向开孔补强计算方法的比较分析

魏 嘉，刘 鑫，徐 明

（1. 中国寰球工程公司辽宁分公司， 辽宁 抚顺 113006； 2. 沈阳航天新光集团有限公司，辽宁 沈阳 110861）

圆筒径向开孔补强计算方法的比较分析

魏 嘉1，刘 鑫2，徐 明1

（1. 中国寰球工程公司辽宁分公司， 辽宁 抚顺 113006； 2. 沈阳航天新光集团有限公司，辽宁 沈阳 110861）

简述了等面积法、分析法和有限单元法三种补强计算方法的基本思想，对这三种计算方法的结果进行了对比分析，讨论了这三种补强计算方法的特点。加深了对标准相关条款的理解，为今后的径向开孔补强设计工作提供了参考。

开孔补强；等面积法；分析法；有限单元法；对比分析

为满足工艺操作及容器本身结构要求，通常需要在容器上设置多个开孔。开孔导致容器强度的削弱，还造成圆筒体与接管的几何不连续处存在较高的应力集中。此外，受开孔接管焊接过程中存在缺陷、安装后存在附加载荷等因素影响，使得开孔补强区域成为容器最常见的失效部位[1]。随着设备不断的大型化，容器上的开孔也随着增大，为解决工程实际中大开孔补强的计算问题，GB150.1～150.4-2011《压力容器》中增加了分析法。用于内压作用下圆筒体径向开孔补强的计算，将常规设计中的开孔率提高到 0.9[2]，解决了之前只能通过有限元法计算的大部分径向大开孔补强问题，极大的方便了大开孔补强计算。本文通过对比三个圆筒径向开孔补强计算实例，讨论等面积法、分析法和有限单元法三种计算方法的特点及适用性，为开孔补强设计工作提供参考。

1 计算模型

表 1中列出了序号 1、2、3 三组圆筒体径向开孔补强的设计条件，表中的尺寸均为有效厚度，焊接接头系数均为 1。为将三种计算结果进行横向比对，表中所列开孔补强结构均未附带补强圈。开孔接管 1圆筒体长度为 4 000 mm，圆筒体两端为标准椭圆形封头，即外压计算长度为 4 233.3 mm。

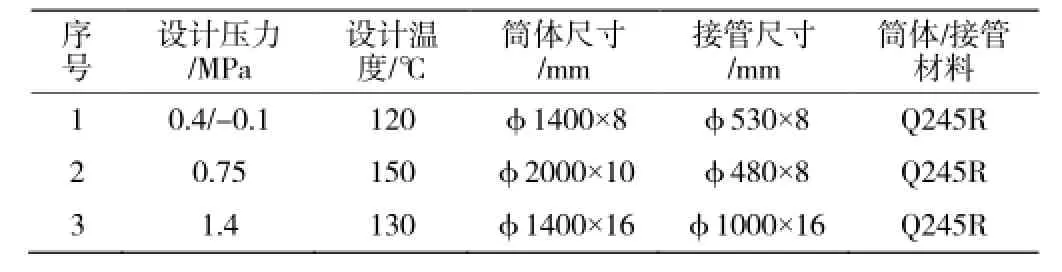
表1 圆筒径向开孔补强设计条件Table 1The opening reinforcement designing conditions for cylinder shell with radial nozzle

2 结果分析

根据 GB150.3-2011中内、外压工况下等面积补强计算公式见式（1）和式（2）[2]，依照以上两式对开孔接管1进行等面积补强计算，计算结果见表2。

表2 开孔接管1等面积补强计算结果Table 2 Results of the equal-area reinforcement for nozzle 1

由表 2 可以看出，内压工况下补强面积Ae大于

从算得的应力数值可以看出，有限单元法计算结果略小于分析法。根据判据，分析法中等效薄膜应力和等效总应力均校核通过，而有限单元法校核的薄膜应力校核未通过。这是因为有限单元法薄膜应力的判定准则是 1.5 倍的许用应力，而分析法中采用的是 2.2 倍材料的许用应力。

一次局部薄膜应力 SII存在应力重分配，提高了结构的承载能力，其危险性要小于总体薄膜应力。此外，一次局部薄膜还存在一定二次应力成分。所以将许用极限由总体薄膜的 1倍提高到 1.5 倍，而这里的1.5 并非经严密推导而得[4]。分析法提出人薛明德等人认为[3]，文献[5]中应力分类法的评定准则是基于简单的梁理论，而实际压力容器多为的板壳结构。在圆筒体开孔补强一类问题中的受力状态比较复杂，不照搬此理论，将圆筒体开孔补强结构中的 SII限制在 1.5 倍许用应力范围内过于保守。通过大量实例计算表明，在绝大多数圆筒开孔补强模型中，将 SII限制在 2.2 倍的许用应力范围内更为合理。可见，文献[5]中基于应力分类法的评定准则是偏保守的。

在分析法的计算模型中将接管与圆筒体看做一个连续的无内伸的整体，所以必须保证焊接接头为全焊透结构。由于接管内伸有利于改善开孔区域的应力分布，故分析法可以保守的计算内伸接管的补强。文献[2]对接管与筒体相贯处圆角大小、焊脚高度、无损检测做了详尽的要求，在设计工作中应对此予以重视。由于等面积和分析法仅考虑了一次加载作用下的结构失效，故不能用于循环载荷作用下的疲劳分析。此外，薛明德等已经得到了管口附加外力与力矩作用下的薄壳理论解及其设计方法[6-9]，并形成规范性文件。故管口附加外力与力矩的开孔补强计算除有限单元法外，还可采用分析法。分析法中除限制开孔率小于 0.9 外，还限制了壳体有效厚度δe和接管有效厚度δet的比值，即 0.5≤δe/δet≤2，这是因为当有效厚度之比超出此范围时，强度校核点偏离了图 2中所示的 A-1路径处。等面积法仅仅考虑了有效补强区内材料的补强面积，没有考虑材料补强的效率，单独的增加筒体或者接管的厚度就可以通过等面积法的计算，但可能导致一次薄膜应力不满足要求，或者导致接管已经变为刚性块而筒体根本就没有得到补强，这是两种做法是不可取的。所以为保证等面积法的有效性，等面积法同样应尽可能使得壳体有效厚度δe和接管有效厚度δet的比值也应控制在 0.5～2 之间。

3 结 论

通过对比圆筒体的径向开孔补强的三种计算方法，得出如下结论：

（1）对圆筒体开孔补强的内、外压两种工况，内压计算通过并不能保证外压校核合格，应分别进行计算和校核；

（2）等面积补强法仅校核截面的薄膜应力，没有考虑了开孔补强中的弯曲应力。在一些较大的开孔补强计算中，等面积法略显冒进，分析法更为合理；

（3）对于圆筒体的大开孔补强，有限单元法算得的应力值略小于分析法，基于应力线性化的评定准则较为保守；

（4）等面积法和分析法较有限单元法计算相对快捷方便，但不能用于疲劳分析。

［1］寿比南, 杨国义, 徐峰,等. GB150—2011《压力容器》标准释义[M].新华出版社, 2012: 141-150.

［2］GB150.1～150.4-2011, 压力容器[S].

［3］薛明德, 黄克智, 李世玉,等. GB150-2011中圆筒开孔补强设计的分析法[J]. 化工设备与管道, 2012, 49(3):1-11.

［4］陆明万, 桑如苞, 丁利伟,等. 压力容器圆筒大开孔补强计算方法[J].压力容器, 2009, 26(3):10-15.

［5］JB/T 4732-1995, 钢制压力容器-分析设计标准（2005 年确认）[S].

［6］薛明德, 李东风, 黄克智. 带径向接管的圆柱壳受支管载荷作用的薄壳理论解[J]. 压力容器, 2004, 21(01):18-24.

［7］Xue M D, Du Q H, Hwang K C, et al. An analytical method for cylindrical shells with nozzles due to internalpressure and external loads—part I: theoretical foundation [J]. Journal ofpressure Vessel Technology, 2010, 132(3): 031206.

［8］杜青海, 薛明德, 黄克智. 柱壳开孔横向轴力作用下的理论解[C].中国钢结构协会海洋钢结构分会2010年学术会议暨理事会第三次会议, 2010.

［9］薛明德, 杜青海, 黄克智. 圆柱壳开孔接管在内压与接管外载作用下的分析设计方法[C]. 全国压力容器学术会议, 2009.

Comparative Analysis on Opening Reinforcement Calculation Methods for Cylindrical Shell With Radial Nozzle

WEI Ji1, LIU Xin2, XV Ming1
（1. HQCEC Liaoning Company, Liaoning Fushun 113001, China；2. Shenyang Aerospace Xinguang Group Co., Ltd., Liaoning Shenyang110861, China）

The basic calculation ideas of equal-area method, analytical method and finite element method for opening reinforcement were briefly described, the calculation results of the three calculation methods were compared and analyzed, characteristics of the three calculation methods were discussed, which could deepen the understanding of the relevant standards andprovide reference for future opening reinforcement designing.

Opening reinforcement; Equal-area method; Analytical method; Finite element method; Comparative analysis

TQ 052

： A

： 1671-0460（2017）02-0359-03

2016-11-20

魏嘉（1984-），男，辽宁抚顺人，工程师，硕士，2016 年毕业于北京化工大学机械工程专业，研究方向：从事压力容器设计。E-mail：weijia@hqcec.com。