布袋除尘系统稳定性量化与改进的数模分析

夏伟宇 朱家明 黄艳红 陈梦倩

（安徽财经大学统计与应用数学学院 安徽蚌埠 233030）

布袋除尘系统稳定性量化与改进的数模分析

夏伟宇 朱家明 黄艳红 陈梦倩

（安徽财经大学统计与应用数学学院 安徽蚌埠 233030）

针对现行垃圾焚烧除尘工艺存在缺乏持续稳定性等重大缺陷的问题，使用层次分析、模糊综合评价等方法，分别构建多级模糊综合评价、参数模型等模型，得到袋式除尘系统稳定性等级并进行了量化分析，再通过曲线拟合得到稳定性，进而作出排放总量和时间相关的函数曲线，运用参数模型得到垃圾焚烧厂扩建规模及检测建议，最后对新型超净除尘替代工艺进行对比分析求解出新工艺的稳定性提高比例。

除尘系统稳定性；除尘效率；层次分析法；多级模糊综合评价；曲线拟合；MATLAB

随着中国城市化的加速，城市垃圾问题日益突出，现行的大型垃圾焚烧厂存在着虽排放浓度达标但排放总量超标的问题，给当地的环境造成了重大的影响。因此，量化分析布袋除尘器运行稳定性问题，不仅能深入揭示现行垃圾焚烧烟气处理技术缺陷以促进除尘技术进步，同时也能优化控制焚烧工况，对运行维护规程的设立有所帮助[1]。

一、布袋除尘系统稳定性的量化

（一）研究思路。影响布袋式除尘系统稳定性包括四个方面：烟气超温超压、除尘效率、烟道和本体漏风以及其他未知因素。为了将其稳定性量化，首先通过使用层次分析法得出影响除尘效率和稳定性的各个指标的重要性程度；再通过模糊综合评价法算出影响除尘效率和稳定性的各因素重要程度模糊集，通过权系数矩阵与评价矩阵的模糊变换得到模糊评判级[2]，这样就能够对稳定性做出定量化表达。

（二）实证分析。

1.建立层次分析模型。本问题要求我们对稳定性进行量化分析，因此，我们需要构建稳定性评价结构[3]，而稳定性评价包含了除尘效率，除尘效率与六个因素有关，所以，在建立二级模糊综合评价之前，首先应建立稳定性的递阶层次结构，如图1所示：

图1 稳定性评价

由于我们无法对本问题直接给出权重，所以通过使用两两比较法导出它们的权重，综合除尘系统制作工艺方面各个专家意见，我们可以分别得到稳定性和除尘效率的比较判断矩阵P=（pij）4×4和Q=（qij）6×6.关于各元素的取值规则见表1[4].

表1 元素与的取值规则

其中，pij与qij也可以取上述各数的中值2,4,6,8及其倒数。

其次计算两个判断矩阵的最大特征根和特征向量，将特征向量归一化作为排序权重，由于该模型没有多层次结构，单层排序权重即总排序权重，也即模糊评价重要性程度集[6]。求出影响稳定性各项因素的权重向量 A=（a1,a2,a3,a4）T和影响除尘效率各项因素的权重向量B=（b1,b2,b3,b4,b5,b6）T.

表2 平均随机一致性指标

2.建立多级模糊综合评价模型。首先作出稳定性的一级结构及除尘效率的二级结构（除尘效率）[7]，分别如图2、3所示：

图2 除尘系统稳定性的一级结构

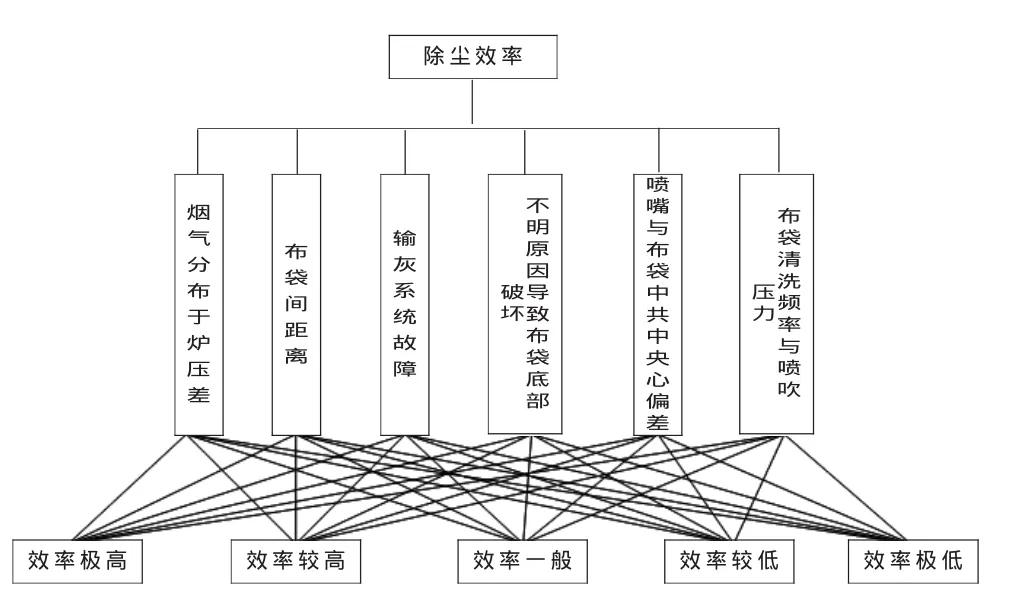
图3 除尘系统稳定性二级结构

首先，确定因素集。稳定性评价除尘效率评价的因素集分别记为：

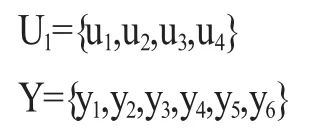
其次，确定评语集。设除尘系统稳定性和除尘效率的评价有极稳定、较稳定、一般、较不稳定、极不稳定。由这五种不同决断构成的集合称为评价集，稳定性和除尘效率的评价级分别记为：

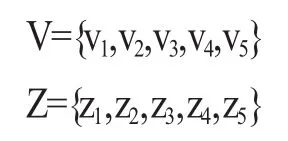
然后，确定各因素的权重。由上述层次分析法可知，稳定性和除尘效率各个因素的权重分别为：

接着，确定模糊综合判断矩阵。

（1）确定稳定性模糊综合判断矩阵。对指标Ui来说，对各个评语的隶属度为V的模糊子集。这里我们选择100名除尘系统制作工艺方面的专家给影响稳定性的四个因素评价。对指标ui的评判记为：

各指标的模糊综合评价矩阵为

其中T矩阵的第二行除尘效率的评判由除尘效率的综合评判结果得出。

（2）确定除尘效率模糊综合判断矩阵。对Vj来说，对各个评语的隶属度为V的模糊子集。这里我们选择100名除尘系统制作工艺方面的专家给影响除尘效率的六个因素评价[8]。对指标Vj的评判记为：

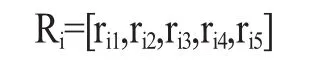
各指标的模糊综合评价矩阵为

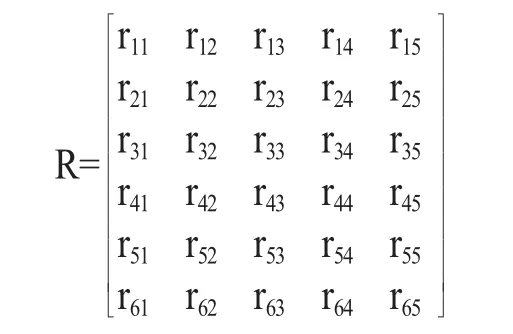
最后，进行综合评判。设除尘系统除尘效率和稳定性的综合评判结果分别为：

综合后的评判可分别看作是和上的模糊向量[9]，分别记为：

根据最大隶属度原则，可判断这个垃圾焚烧发电厂除尘系统的稳定性等级。

（三）结果分析。由于除尘系统的稳定性与烟尘排放浓度成反比，烟尘排放时间与烟尘排放浓度成正比[10]，在此，我们首先建立了一个烟尘排放浓度随时间变化的一元二次函数：

其中,f：烟尘排放浓度；s：除尘系统的稳定性（0＜s＜1）；t：时间（单位：天）；C：常数.

其次，我们通过定期对某焚烧厂周围烟尘排放浓度的测定，用MATLAB拟合得出该除尘系统的稳定性与常数C[11]。为了得到具有普遍适用性的稳定性量化公式，我们需要将“稳定性极好”与“稳定性较好”分别赋予参数α、1-α，则除尘系统稳定性量化后的表达式为：

因此，针对任意一个焚烧发电厂的布袋式除尘系统，只要知道其稳定性的综合评判结果，便能得出其稳定性量化后的数字[12]。

二、焚烧厂扩建规模的确定

（一）研究思路。为了将除尘系统稳定性量化后的表达式与焚烧厂扩建规模的环境允许上限相联系，首先建立一个烟尘排放浓度随时间变化并与稳定性相关的函数[13]，其次将烟尘排放总量与烟尘最大允许排放量对比，得出焚烧厂扩建规模的环境允许上限并基于分析结果提出环境保护综合监测建议方案。

（二）实证分析。由公式（1）可知，除尘系统稳定性s越大，烟尘排放浓度f(t)的上升就越慢，如图4所示。

图4 除尘系统稳定性不同时烟尘排放浓度随时间的变化曲线

而在实际生活中，烟尘排放浓度随着时间的增加而变大，但烟尘排放总量不能超标，因此，焚烧厂必须在一定时间内对除尘系统进行修复[14]，此时，烟尘排放浓度会降到最低，所以，烟尘排放浓度随时间变化的实际函数应为一个周期性函数F(t)：

拟合曲线如图5所示：

图5 实际烟尘排放浓度随时间的变化曲线

由于给定焚烧厂周边范围单位面积排放总量限额，因此，假设规定该焚烧厂固定面积下在时间t内烟尘最大总排放量为D，实际烟尘排放总量为D0,焚烧厂原规模等效为烟气排放总量为G0，烟尘排放浓度为C=f(t),扩建规模系数为k。

已知烟尘排放浓度和扩建后烟气排放总量分别为：

由于焚烧厂在t时间内的烟尘排放总量不能超标，所以首先利用微积分方法找出烟尘排放浓度随时间变化的实际函数F(t)在t时间内积分的最大值，为：

可得：焚烧厂t时间内烟气最大排放量为：

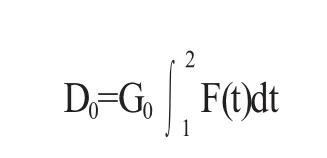
由于烟气总排放总量不能超过规定的限额，所以得出焚烧厂的扩建规模为：

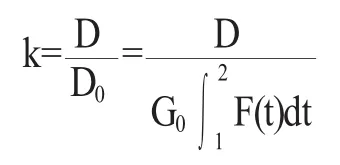
（三）结果分析及政策建议。为了增加对焚烧厂烟尘排放监测的公平性，我们向政府建议选取若干名专家、环监局专业人员，并从各个焚烧厂抽取一定人数组成团队，对该地区的各个焚烧厂烟尘排放进行系统性专业监测，并让企业自行监测发布污染信息以作参考，建立质量保证程序和措施[15]。对于监测指标，我们建议从以下两个方面来考虑：

首先是从烟气排放总量来考察，根据烟气排放流速的公式：

由公式（2）可知，烟气排放的流速决定烟气排放总量，由于烟气排放总量很难测定，因此，为了方便监测人员的测量，我们建议专家团队不定期检测焚烧厂的烟气排放流速是否合乎标准，从而可以判断该焚烧厂的烟气排放总量是否超标。

其次是从烟尘排放浓度来考察，由于焚烧厂烟尘排放浓度随时间呈周期性变化，因此，我们需要各焚烧厂提供除尘系统定期修复的时间，建议政府部门在焚烧厂定期修复之前测定该厂烟尘排放的浓度，从而判断该焚烧厂的烟气排放浓度是否超标。

烟尘排放的控制与各焚烧发电厂自身除尘系统的改进与提高稳定性息息相关，同时也离不开政府强有力的监控，因此，政府应采取科学的方法加大对焚烧发电厂烟尘排放的监测以实现可持续发展的战略[16]。

三、改进后的除尘系统稳定性提升率的确定

（一）研究思路。由于新工艺对除尘系统稳定性的改进主要是对其影响因素的完善，所以分析改进后的新型超净除尘替代工艺的稳定性与前面的思路基本一致，数据的处理方法也是一致的，还是运用层次分析法和多级模糊综合评价法来求出稳定性数值[17]。但是在比较两种除尘工艺稳定性性能是否有显著性差异时，我们给出了稳定性性能提升率的数学方程式，最后我们得出改进的除尘系统的稳定性提升率的精确值。

（二）实证分析。首先确定稳定性一级模糊综合评价结果，即除尘效率的模糊综合评价结果，再在一级模糊综合评价结果基础上对改进后的除尘系统进行二级模糊综合评价。我们知道新型超净除尘系统采用了固体滤料，克服了老式布袋除尘系统布袋容易破损的弊端，所以改进后的超净除尘系统只是改变了除尘系统的除尘效率，进而影响除尘系统的稳定性。将改进后的超净除尘系统的综合评判结果记为：

同理，我们需要对改进后的除尘系统的稳定性进行量化，根据稳定性量化模型，我们可以得出改进后的除尘系统的稳定性为：

（三）结果分析。根据数学知识，我们建立了新除尘工艺稳定性提高率的数学关系式，记为

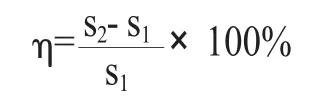
因此，只要知道不同除尘系统稳定性量化后的数值，便可求出除尘工艺稳定性提高率。

四、结语

本文基于现行垃圾焚烧除尘工艺存在缺乏持续稳定性等重大缺陷的问题，构建多级模糊综合评价等模型得到袋式除尘系统稳定性性能的量化，作出排放总量和时间的相关函数曲线，得到垃圾焚烧厂扩建规模并给出环境保护综合监测建议方案，最后对新型超净除尘替代工艺进行对比分析求解出新工艺的稳定性提高比率。同时为垃圾焚烧厂规模的确立提供了新思路，并为烟尘排放浓度的检测给出了建议，得到了对未来环保发展的有益启示。

[1]2016年“深圳杯”数学建模挑战赛题目[J].数学建模及其应用,2016（3）.

[2]中国新闻网.2016/05/09.http://www.crra010.com/articles/ 22272.html.

[3]中华人民共和国环境保护部.2014年全国大、中城市固体废物污染环境防治年报[N].中国环境报,2015-01-05.

[4]杨桂元.数学建模[M].上海：上海财经大学出版社, 2015.

[5]张小红.模糊数学与Rough集理论[M].北京：清华大学出版社,2013.

[6]谢季坚.模糊数学方法及其应用[M].武汉：华中科技大学出版社,2013.

[7]脱友才,邓云,王旭.多级模糊模式识别方法用于河流水质评价[J].四川环境,2007(1).

[8]卢平.用模糊数学方法评价采场稳定性[J].南方冶金学院学报,1989(2).

[9]周科平.采场顶板稳定性的模糊综合评价[J].湖南有色金属,1994(1).

[10]李冬梅,田娱嘉,郭阳.布袋除尘器滤袋使用寿命的影响因素分析[J].热力发电,2013(4)

[11]朱杰.影响布袋除尘器除尘效率和滤袋寿命的因素分析[J].装备制造技术,2013(6).

[12]姜启源,谢金星,叶俊.数学模型[M].北京：高等教育出版设,2015.

[13]杨桂元,朱家明.数学建模竞赛优秀论文评析[M].合肥：中国科学技术大学出版社，2013.

[14]吴礼斌.经济数学实验与建模[M].北京：国防工业出版社,2013.

[15]司守奎,孙玺菁.数学建模算法与应用[M].北京：国防工业出版社,2015.

[16]张娟娟，朱家明，苏思美.垃圾减量分类中社会及个体因素的量化分析[J].宜春学院学报,2014(3).

[17]赵天梅，朱家明，张娟娟.基于分层抽样的垃圾减量分类效果研究[J].衡水学院学报，2014(8).

[责任编辑 郑丽娟]

QuantificationandImprovementModelofStabilityofBagDustRemoval System

Xia Weiyu Zhu Jiaming Huang Yanhong Chen Mengqian

(School of Statistics and Applied Math,Anhui University of Finance and Economics,Bengbu,Anhui 233030)

In order to solve the shortcomings of the existing incineration and dust removal technology,this paper uses hierarchical analysis and fuzzy comprehensive evaluation method to construct multi-level fuzzy comprehensive evaluation and parameter model,and obtains the stability level of bag dust removal system.The quantitative analysis is carried out and the stability is obtained by curve fitting.Then the function curve of total discharge and time is made,and the scale of waste incineration plant is expanded by using the parameter model. Finally,the new method is compared and solved in order to obtain the ratio of the stability of the new technology.

stability of the dust removal system;dust removal efficiency;analytic hierarchy process; multi-level fuzzy comprehensive evaluation;curve fitting;MATLAB.

TF547

A

2095-0438（2017）03-0140-05

2016-11-07

夏伟宇(1996－)，女，安徽繁昌人，安徽财经大学统计与应用数学学院学生，研究方向：数学与应用数学；朱家明（1973-），男，安徽泗县人，安徽财经大学数学建模实验室主任，副教授，硕士，研究方向：应用数学与数学建模。

国家自然科学基金项目（11601001）。