2016年北京理科第19题的再探究

北京市第十二中学 (100071) 刘 刚 赵 毅

2016年北京理科第19题的再探究

北京市第十二中学 (100071) 刘 刚 赵 毅

1.试题回放

2016北京理科第19题是：

(Ⅰ)求椭圆C的方程；

(Ⅱ)设P是椭圆C上一点，直线PA与y轴交于点M，直线PB与x轴交于点N．求证：|AN|·|BM|为定值．

文[1]用了三种解法得出了该题(Ⅱ)问的答案，并推广得到了下面的定理：

实际上，定理中A,B两个点为一组特殊共轭直径的顶点，如果A,B为任意一组共轭直径的顶点，也会有相应的结论．

2.再探究

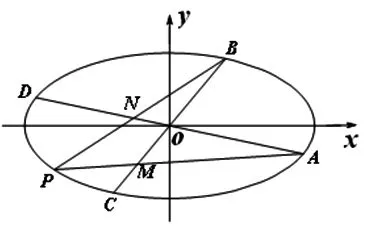
图1

证明:(1)当AD，BC有一直径所在直线斜率为0时，同上述定理，即|AN|·|BM|=2ab，所以结论成立；

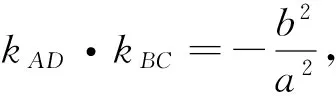
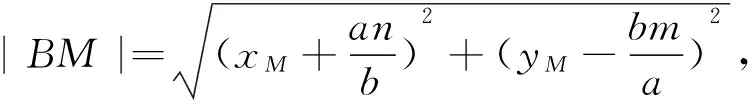
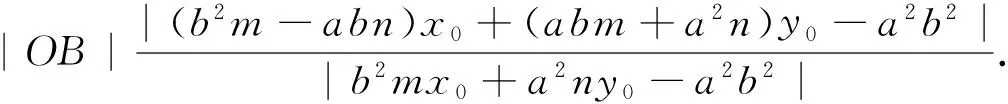
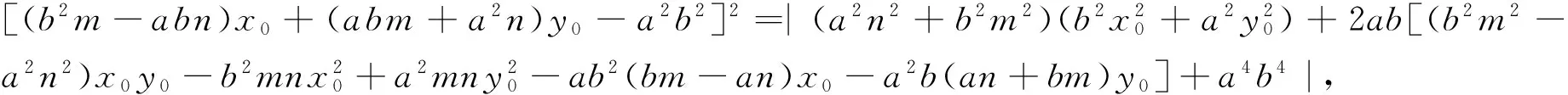
因为|b2mx0+a2ny0-a2b2|·|nx0-my0+ab|=

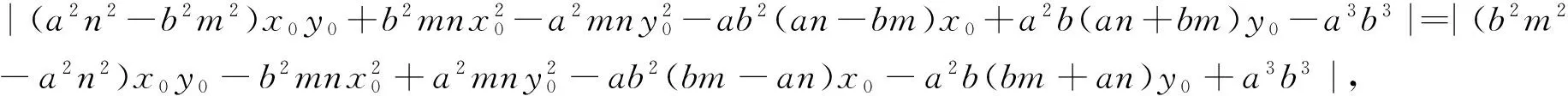
=2|OA|·|OB|．当x0=m时，经检验结论也成立．综上|AN|·|BM|=2|OA|·|OB|．

[1]夏迎雪，于兴江．实践剖析 突破定值问题——2016北京理科第19题的多解及探究[J]．中学数学研究(江西)，2016,9．