外辐射源雷达多普勒徙动补偿新方法

张丹， 吕晓德， 杨鹏程， 柴致海， 岳琦， 杨璟茂

(1.中国科学院电子学研究所， 北京 100190；2.微波成像技术国家重点实验室， 北京 100190；3.中国科学院大学， 北京 100049)

0 引言

外辐射源雷达本身不发射电磁波，通过环境中已有的外部辐射源，对目标进行定位及跟踪，具有隐蔽性强、成本低、抗干扰能力强等诸多优点，因此成为各国的研究热点[1-4]。外辐射源雷达进行目标检测时，对信号进行长时间的相干积累是一种有效的手段，但会引起徙动问题。在外辐射源雷达双基/多基模型下，目标径向运动引起距离徙动，目标切向运动以及存在的加速度引起多普勒徙动，严重影响积累增益。目前，雷达图像中的Keystone方法[5]可很好地解决外辐射源雷达中的距离徙动问题，但多普勒徙动问题仍在研究阶段。

针对多普勒徙动问题，现有的典型方法主要分为两种，一种方法是直接估计二次项调频率，如离散多项式相位变换[6]、WVD-Hough变换[7]，但前者要求目标输入信噪比要高，后者算法计算量很大；另一种方法是直接遍历搜索二次项调频率，如分数阶傅里叶变换[8]、MDCFT[9]，但这类方法由于未知目标运动状态，所需的计算量也很大，并且方法不适用于多目标场景。针对已有方法计算量大、实现较困难的问题，本文提出STFT-Hough[10-11]方法，其中STFT方法采用无交叉数据滑窗方式截取信号，并在时间单元上采用只取多普勒频率峰值、其他置零的方式。该种方法不仅可以估计出信号的多普勒二次项调频率并实现对目标的补偿，同时大大降低数据处理的计算复杂度，提高了处理速度。

1 外辐射源雷达回波信号模型

外辐射源雷达双基模型如图1所示，TX为发射站，RX为接收站，β为目标初始位置与两站之间所成的双基角，RT和RR分别为目标到发射站和接收站的初始距离。目标运动t时间后，由M点转移到N点，δ为目标运动方向与双基角平分线的夹角，RT(t)，RR(t)分别为目标到发射站、接收站的瞬时距离，L为两站之间的基线长度。目标初始速度为vg，运动加速度为a。

图1 外辐射源雷达双基模型

经Keystone方法校正完距离徙动后，回波信号模型为

yr(t)=A0s[t-τ0]ej2πfdte-jπαdt2

(1)

式中，A0为幅度常数，s(t)为参考信号，τ0为回波时延中常数项。

多普勒频率fd为

(2)

二次项调频率αd为

(3)

式中，λ为信号波长。因此可以得出：回波信号的多普勒频率徙动量与调频率αd有直接关系，即分别与信号波长λ、速度vg、加速度a、回波模型RT,RR,δ,β等有关。当目标有切向速度或者目标没有切向速度但本身有加速度时，都会产生多普勒徙动。例如，当工作频率为674 MHz，匀速运动目标径向速度为5.66 m/s，切向速度为350 m/s，单基距离在150 km时，调频率αd为3.26 Hz/s，对应1 s积累时间的增益损失约4.5 dB，对应5 s积累时间的增益损失约12 dB。

本文接下来使用STFT-Hough方法估计二次项调频率并补偿，该方法不仅可以解决目标多普勒徙动问题，并且运算量比较小，可以实时实现。

2 STFT-Hough处理算法

2.1 算法原理

由式(1)得，外辐射源回波信号在多普勒频率(方位向)上是线性的，因此方位向上的信号可近似为线性调频信号。之前有观点[7]提出使用WVD-Hough变换解决多普勒徙动问题，但考虑到该方法计算量比较大，不能在工程上实时实现，因此本文采用无交叉数据滑窗并取多普勒峰值的STFT-Hough方法，解决多普勒徙动补偿和计算量大的问题。

STFT是时频分析中比较基础和经典的方法。定义[10]如式(4)：

(4)

式中，x(n)为信号函数，w(n)为一个窗函数，其作用是取出x(n)在n时刻附近的一小段信号进行傅里叶变换，当n变化时，窗函数随n移动，从而得到信号频谱随时间n变化的规律。

线性调频信号经过STFT变换，时频域呈现一条直线，Hough变换通过在参数空间里进行简单的累加统计，寻找累加器峰值并检测出直线。

如图2所示，直线l斜率为k，截距为b，在参数空间ρ-θ中，该直线上的点都映射为同一个点，这一点的坐标为

ρ=xcosθ+ysinθ

(5)

式中，半径ρ为原点到直线的距离，θ为半径ρ与x轴的夹角。由于直线l上的所有点在参数空间ρ-θ中幅值积累成一点，因此会形成峰值点，从而直线l被检测出。此时，可以得到直线斜率k为

k=-cotθ

(6)

由式(6)进一步可估计出信号二次项调频率αd为

(7)

式中， Δf为STFT变换中时间单元上的多普勒频率分辨率， Δt为STFT变换的时间分辨率。因此利用STFT-Hough方法，可以通过信号积累的方式，估计并补偿信号的二次项调频率。但时频分析方法的计算量是比较大的，针对计算量问题，本文特别作了以下设置和处理。

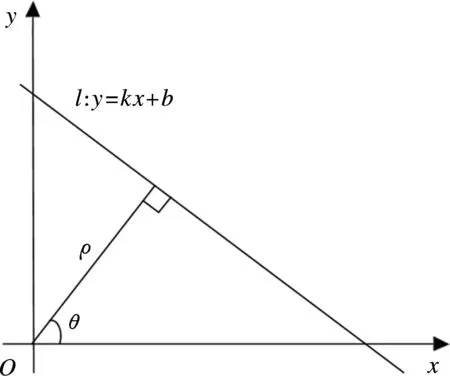
图2 Hough变换原理图

STFT的时频分析方法中，w(n)是滑动窗，其滑动距离可以自由设置，可以设为1/4窗长、1/2窗长等距离[10]，为了减小计算量，本文中w(n)滑动距离设为整个滑动窗长度，这本质上是对信号分段截取并对其加窗实现傅里叶变换，式(4)变换为

STFTX(n,w)=FFT[x((n-1)·N+

(8)

式中，N为每段信号的长度，M为信号总长度。这种直接对信号分段并加窗的方式，充分利用了整个数据长度，虽然时间分辨率会略低一些，但不影响长时间相参积累中对线性调频率的检测，这些有限的时间单元使得下一步Hough变换计算复杂度降低。对某一距离单元上的信号采用分段加窗并进行傅里叶变换的方式，时频分析结果如图3所示。

(a)STFT变换结果

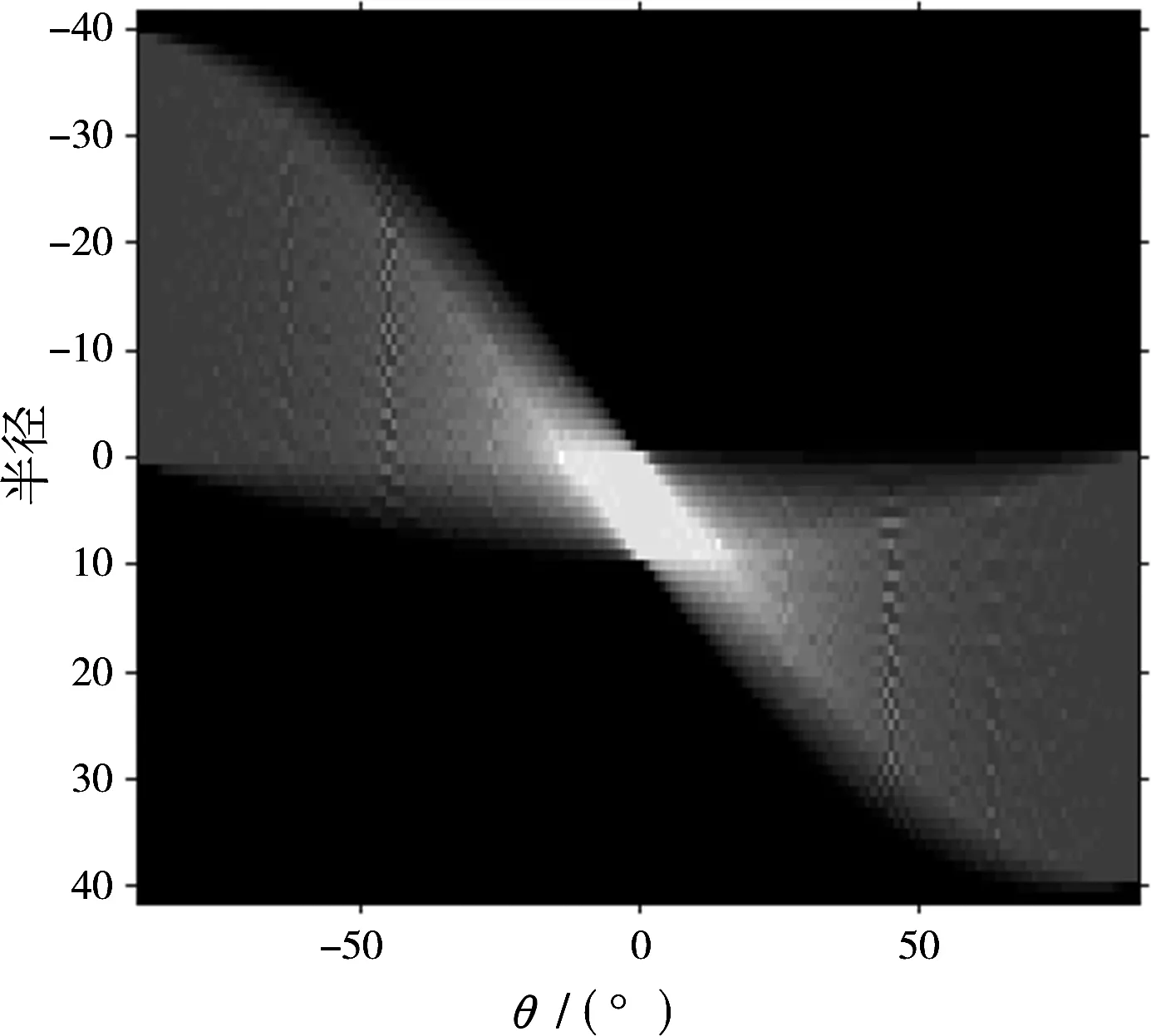
(b)Hough变换结果图3STFT-Hough变换结果

由图3(a)可以看出，在每个时间单元上，目标多普勒信息会有副瓣，映射到Hough变换域。如图3(b)所示，会出现多个亮点，影响观测，导致不能正确估计目标多普勒频率的二次项。因此，该文STFT方法采用在时间单元上取多普勒峰值、其他多普勒频率置零的方式，实现下一步Hough变换。这种做法不仅可以估计出调频率，同时将非峰值点置零，可大大减小后续Hough变换的计算量。并且，当目标非常微弱时，会在一些时间单元上出现噪声淹没目标的情况，使得目标无法在时频域呈现良好的线性关系。采用在时间单元上取多普勒峰值、其他多普勒频率置零的方式，依然可以根据一些时间单元上的最大值，经过Hough变换，积累出最亮点目标。

STFT-Hough变换算法流程图如图4所示。

图4 STFT-Hough变换算法流程图

2.2 计算量分析

表1 计算复杂度对比

由于本文中STFT-Hough方法是在时间单元上取多普勒峰值，而不是利用阈值检测的方式估计二次项并补偿，所以此方法适用于单个距离单元内只有一个运动目标的场景，这种场景在实际中是比较常见的。同时，本文中STFT的做法实质是对信号依次加窗并作傅里叶变换，因此，加窗长度不能太短，否则每个时间单元上对应的多普勒频率分辨率会很低，导致估计出的目标没有在积累时间上出现多普勒徙动，从而无法对信号作出正确的估计和补偿。同样，信号的整体积累时间也不能太短，否则信号的时频线性效果不理想。因此本文所提的STFT-Hough变换适用于常见的长时间相参积累中，一般保证加窗的长度高于0.5 s的数据长度，信号整体积累时间在5 s以上，这样所估计的二次项多普勒调频率与理论值非常接近。

3 仿真和实测数据分析

3.1 仿真分析

前文中针对外辐射源雷达运动目标的多普勒徙动问题，提出了一种STFT-Hough解决方法，本节重点通过仿真和实测数据验证该方法的有效性。

结合实际场景，设检测系统虚警率为10-6，发现概率为0.8，对应最小检测因子为13 dB。基于DTTB数字电视信号单载波模式(信号带宽8 MHz，采样率8 MHz)，首先仿真一个运动目标，输入信噪比为-60 dB，二次项调频率为3 Hz/s。由于目标非常微弱，需要对信号进行长时间的相参积累。对信号进行5 s的相参积累，方位向信号长度M为600，如图5(a)所示，目标淹没在噪声中，无法被识别出。图5(b)是对信号所在的距离单元作STFT(将信号分成10段)的结果，在图中可以明显看出一条直线，尽管由于目标输入信噪比较低，有些点并不在直线上。图5(c)是在图5(b)的基础上再进行Hough变换的结果，从图中能够根据目标对应的最大值点，估计出目标的多普勒二次项调频率αd为3.07 Hz/s。图5(d)是对目标进行二次项调频率补偿后的结果，通过STFT-Hough方法，目标多普勒调频率几乎得到精确补偿，信噪比达到14.5 dB，大于系统最小检测因子，可以被检测出。

(a)直接FFT结果

(b)STFT时频分析结果

(c)Hough变换结果

(d)STFT-Hough变换结果图5仿真结果图

图6表示了目标输入信噪比与多普勒二次项调频率估计精度的关系，横坐标为输入信噪比，纵坐标为20次单独实验后所取的精度误差平均值。由图6可以看出，对于输入信噪比为-60 dB以上的运动目标，STFT-Hough变换方法可以很好地估计出目标的二次项调频率并进行补偿，尤其可以估计出输入信噪比为-55～-60 dB这一区间的微弱目标的调频率。当输入信噪比低于-60 dB时，估计性能会下降，原因是此时噪声成分太大，时频分析直线已经无法呈现，故无法将目标积累起来并估计出参数。

图6 输入信噪比与估计精度的关系

3.2 实测数据结果

以下是一组实测数据，数据中有4个目标，且都有多普勒徙动问题。实测数据的相关参数如表2所示。

表2 实测数据相关参数

图7是实测数据处理图。

图7(a)表示对5 s的实测数据进行常规方法处理(5 s Keystone变换+直接FFT)，图7(b)表示加入STFT-Hough方法的处理(5 s Keystone变换+STFT-Hough+直接FFT)。由图7可以看出，采用STFT-Hough方法对目标进行多普勒徙动补偿是有效的，4个目标信噪比对比情况如表3所示。

图7和表3表明，改进的STFT-Hough方法处理实测数据中多个目标的多普勒徙动问题是有效的。同时，用MATLAB平台处理该实测数据时，不对数据进行多普勒徙动补偿，运行时间为255 s， 加入改进的STFT-Hough方法，运行时间增加了9 s， 这说明本文中STFT-Hough变换的方法运算速度是比较快的，可以保证系统实时实现。

(a)直接FFT变换结果图

(b)STFT-Hough变换后结果图图7实测数据结果图

目 标直接FFT/dBSTFT-Hough+FFT/dB提高增益/dB1(距离单元686)2(距离单元3243)3(距离单元3783)4(距离单元5339)23.4818.0813.5839.1832.825.523.842.59.327.4210.223.32

4 结束语

本文针对外辐射源雷达长时间相参积累中运动目标出现的多普勒徙动问题，提出了一种STFT-Hough变换方法，该方法的STFT采用无交叉数据滑动窗对信号分段，并依次作FFT变换，得出方位向信号的时频分析结果，并在时间单元上使用多普勒频率取峰值、其他置零的方式，进行下一步Hough变换。这一改进方法不仅能很好地估计出信号的二次项调频率并进行补偿，并且与以往的WVD-Hough变换等时频分析方法相比，大大降低了计算量，可以在系统中实时实现。仿真和实测数据也说明了该方法的有效性。

[1]万显荣,邵启红,夏鹏,等. 数字地面多媒体广播外辐射源雷达微多普勒效应实验[J]. 系统工程与电子技术, 2016, 38(11):2499-2504.

[2]彭章友,陈文涛,李林霄. 基于外辐射源特征信息的Logistic多星累积算法[J]. 电子测量技术, 2016, 39(8):172-176.

[3]YU De, MA Hong, CHENG Li, et al. Method and Field Experiment of Target Tracking via Multi-Static Doppler Shifts in High-Frequency Passive Radar[J]. IET Radar, Sonar & Navigation, 2016, 10(7):1201-1212.

[4]KETPAN W, SELLATHURAI M. Compressive Sensing-Based 3D Signal Extraction for MIMO Passive Radar Using OFDM Waveforms[C]∥2016 IEEE International Conference on Communications, Kuala Lumpur, Malaysia:IEEE, 2016:1-6.

[5]关欣,胡东辉,仲利华,等. 一种高效的外辐射源雷达高径向速度目标实时检测方法[J]. 电子与信息学报, 2013, 35(3):581-588.

[6]宁志腾. 前视双基地SAR多普勒参数估计与运动补偿研究[D]. 成都：电子科技大学, 2015.

[7]关欣,仲利华,胡东辉,等. 一种基于RSPWVD-Hough变换的无源雷达多普勒展宽补偿方法[J]. 雷达学报, 2013, 2(4):430-438.

[8]王瑞,马艳. 基于分数阶傅里叶变换的线性调频脉冲信号波达方向估计[J]. 兵工学报, 2014, 35(3):421-427.

[9]GUO Xin, SUN Hongbo, WANG Shengli, et al. Comments on Discrete Chirp-Fourier Transform and Its Application to Chirp Rate Estimation[with Reply][J]. IEEE Trans on Signal Processing, 2002, 50(12):3115-3116.

[10]丁玉美,阔永红,高新波. 数字信号处理：时域离散随机信号处理[M]. 西安：西安电子科技大学出版社, 2002:174-175.

[11]张平,贺鹏程,张向龙. 基于Wigner-Hough变换和中值滤波的加速度估计[J]. 雷达科学与技术, 2012, 10(3):290-293.