圆有向图的(1,2)步竞争图中存在哈密尔顿圈的条件
崔 建,叶 旺
(1.山西医科大学汾阳学院 基础医学部,山西 吕梁 032200; 2.山西大学 数学科学学院,太原 030000)
圆有向图的(1,2)步竞争图中存在哈密尔顿圈的条件
崔 建1,叶 旺2
(1.山西医科大学汾阳学院 基础医学部,山西 吕梁 032200; 2.山西大学 数学科学学院,太原 030000)
针对圆有向图的(1,2)步竞争图的结构,提出了竞争图中是否存在哈密尔顿圈;通过特殊到一般的方法得到如下结论:对于阶数n(n≥5)的强连通圆有向图的(1,2)步竞争图中存在哈密尔顿圈,而其余情形的圆有向图的(1,2)步竞争图中则不存在哈密尔顿圈。
圆有向图;(1,2)步竞争图;哈密尔顿圈
0 引 言
1968年美国著名分子生物学家Cohen,首先提出了竞争图的概念,指出生态系统中的食物链和食物网都可以看作有向图,其中的所有物种可看作顶点集,u到v有一条有向弧当且仅当物种u以物种v为食物。若物种x和物种y同时以物种z为食物,则x与y竞争。竞争图除了被应用在生态系统上外,在无线电广播研究,噪声信通道信研究及编码理论等方面也被广泛应用[1]。自Cohen提出竞争图后,很多衍生概念陆续被人们提出,Lundgren等人[2]提出了公敌图的概念;Cho等人[3]提出了m- 步竞争图的概念;Lundgren和Merz[4]提出了控制图的概念;Factor和Merz[5]提出了(1,2)步竞争图及(i,k)步竞争图的概念,并完全刻画了竞赛图(1,2)步竞争及(i,k)步竞争图的结构。本文拟研究圆的有向图的(1,2)步竞争图中存在的哈密尔顿圈的条件。
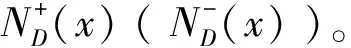
如果xy∈A(D)或者yx∈A(D),那么x和y是相邻。如果n个顶点的有向图D的顶点可标号为v0,v1,…,vn-1使得对每个i,总有N+(vi)={vi+1,vi+2,…,vi+d+(vi)}和N-(vi)={vi-d-(vi),vi-(vi)+1,…,vi-1}(所有下标均取模n,以后不再重复说明),称D是圆有向图,称序是v0,v1,…,vn-1。
有向图D=(V,A),对于每个X⊆V且X≤k-1,如果D-X是强连通的,则D是k强连通的,简称D是k强的。如果D是k(k≥2)强的,那么D也是k-1强的。
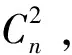
设D是一个圆有向图,v0,v1,…,vn-1是圆有向图D的一个圆坐标,连续的顶点集{va,va+1,…,va+b}(其中a∈{0,1…,n-1},b>1)在D中构成一个扁条,记住B,如果这些顶点满足式(1)(2)(3):
d+(va)=…=d+(va+b-2)=2
(1)
d-(va+2)=…=d-(va+b)=2
(2)
d-(va+1)=…=d+(va+b-1)=1
(3)
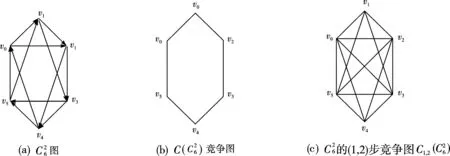
图以及它的竞争图和(1,2)步竞争图Fig.1 ,the competition graph C()and the step (1, 2) competition graph
显然,va,va+b在D中是割点,至少有一个割点的圆有向图D总是可以删去一些出度大于3的顶点和入度大于3的顶点之间的狐,得到一些扁条,这些扁条的并构成的圆有向图,记作D′。图2(a)是下标a=0,b=5的扁条B,图2(b)(c)分别是该扁条B的竞争图和(1,2)步竞争图。
设G=(V,E)是一个无向图,V是G的顶点集,E是G的边集,包含G中的每个顶点的圈叫作G的哈密尔顿圈。
设D=(V,A)是一个有向圈,D=(V,E)是一个无向圈。如果无向图G=(V,E)满足,V(G)=V(D)并且xy∈E(G),当且仅当D中存在顶点z≠x,y使得dD-y(x,z)=1,dD-x(y,z)=1,那么称G为D的竞争图,记为C(D)。
设T是l个顶点的竞赛图,称D=T(S1,S2,…,Sl)是T的扩充竞赛图,C1,2(T)是T的(1,2)步竞争图,并称H=C1,2(T)[S1,S2,…,Sl]是D的同等扩充。

图2 a=0,b=5的扁条B以及它的竞争图C(B)和(1,2)步竞争图C1,2(B)Fig.2 The flat bar whena=0,b=5,the competition graph C(B),and the step (1, 2) competition graphC1,2(B)
此外,研究强连通圆有向图的竞争图及有向图的(1,2)步竞争图中存在哈密尔顿圈的条件。
1 准备知识
引理1D是一个有向图,D′是D的子有向图,则C(D′)⊆C(D)。
由引理1,可得到推论1。
推论1D是一个有向图,D′是D的子有向图,则C1,2(D′)⊆C1,2(D)。

由竞争图和(1,2)步竞争图的定义,显然有以下的引理。
引理3x是有向图D的一个顶点,则N-(x)诱导出C(D)的完全子图。
引理4D是一个有向图,C(D)是D的竞争图,C1,2(D)是D的(1,2)步竞争图,则C(D)⊆C1,2(D)。
2 存在哈密尔顿圈的条件分析之一

定理1 若D是一个n阶的2强连通的圆有向图,则C(D)中存在哈密尔顿圈。
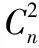
推论2 若D是一个n阶的2强以上的圆有向图,则C(D)中存在哈密尔顿圈。
定理2 设D是一个n阶的1强连通的圆有向图,且D中只有一个割点记作vi。若D中的顶点满足d-(vi+j)≥3(j≠1,2),则C(D)中存在哈密尔顿圈。
证明不妨设v0是阶为n的1强连通圆有向图D的割点,由d-(vj)=d-(v0+j)≥3(j≠1,2),得{vj-3vj-2vj-1}⊆N-(vj)(j≠1,2)。由引理2.4,{vj-3vj-2vj-1}(j≠1,2)构成的完全图是C(D)的子图。
当n是奇数时,v0v2v4…vn-1vn-2vn-4…v3v1v0在C(D)中是哈密尔顿圈;当n是偶数时,v0v2v4…
vn-2vn-1vn-3…v3v1v0在C(D)中是哈密尔顿圈。再由引理2,命题得证。
根据上面的证明,猜想下面的结论是正确的。
猜想1 若强连通圆有向图D中有k(0 定理3 若D是n阶的2强以上的圆有向图,则C1,2(D)中存在哈密尔顿圈。 当D是一个n阶的1强的圆有向图时,考虑C1,2(D)中是否存在哈密尔顿圈。若C1,2(D)中存在哈密尔顿圈,D应该满足什么样的条件。 引理5 若vi是1强的圆有向图D中的割点,则d+(vi-1)=1且d-(vi+1)=1。反之也成立。 引理6 设连续的顶点集{va,va+1,…,va+b}(其中a∈{0,1,…,n-1},b>1)在圆有向图D中构成一个扁条B,则C1,2(B)是由以下几种无向图构成: 定理4 若n(n≥5)阶的1强连通有向图D中下标相邻的顶点不同时是割点,则C1,2(D)中存在哈密尔顿圈。 证明情形1:圆有向图D中只有一个割点。 不妨设v0是D中的割点,删去D中所有出度大于2的顶点和入度大于2的顶点之间的弧,得到新的圆有向图,记作D′。连续的顶点集v0,v1,…,vn-1,v0在D′中诱导出一个扁条。因为n≥5,由引理6(3),C1,2(D′)中存在哈密尔顿圈。 情形2:圆有向图D中有两个以上割点。 删去D中所有出度大于2的顶点个入度大于2的顶点之间的弧,得到新的圆有向图,记作D′。此时的D′是由一系列扁条的并集构成。 又因为va1+b1-2→va1+b1→va1+b1+2,va1+b1-1→va1+b1→va1+b1+2,va1+b1+1→va1+b1+2,由(1,2)步竞争图的定义,va1+b1-2va1+b1+1,va1+b1-1va1+b1+1分别是C1,2(D′)中的边。 当b1=2时,va1+1va1va1+b1+1va1+b1是C1,2(D′)中的一条路。 当b1>2时,va1+1va1va1+2va1+3…va1+b1-1va1+b1+1va1+b1是C1,2(D′)中的一条路。 又因为va2+b2-2→va2+b2→va2+b2+2,va2+b2-1→va2+b2→va2+b2+2,va2+b2+1→va2+b2+2,由(1,2)步竞争图的定义,va2+b2-2va2+b2+1,va2+b2-1va2+b2+1分别是C1,2(D′)中的一条路。 ∪{var+br}。 又因为var+br-2→var+br→var+br+2,var+br-1→var+br→var+br+2,var+br+1→var+br+2,由(1,2)步竞争图的定义,var+br-2var+br+1,var+br-1var+br+1分别是C1,2(D′)中的边。 当br=2时,var+1varvar+br+1var+br是C1,2(D′)中的一条路。 当br>2时,var+1varvar+2var+3…var+br-1var+br+1var+br是C1,2(D′)中的一条路。 把上述的r条路按照事先安排好顺序连起来就构成C1,2(D′)中的一个哈密尔顿圈,再由推论1,C1,2(D′)中存在哈密尔顿圈。 当n阶强连通圆有向图D中下标相邻的顶点同时是割点时,C1,2(D′)中是否还有哈密尔顿圈存在。先证明引理7和引理8。 引理7 若n阶强连通圆有向图D中连续出现3个以上下标相邻的顶点同时是割点,则C1,2(D′)中不存在哈密尔顿圈。 引理8 若n阶强连通圆有向图D中出现两对以上下标相邻的顶点同时是割点,则C1,2(D)中不存在哈密尔顿圈。 由引理7和引理8,只需要讨论下标相邻的两个顶点在圆有向图D中同时是割点的情形。 定理5 若n(n≥5)阶强连通圆有向图D下标相邻的顶点同时是割点且有一个割点的出度大于2,其余的都不是割点,则C1,2(D)中存在哈密尔顿圈。 在圆有向图D中,因为d+(v0)>2,所以有vn-1→v0→v3,v1→v3,v2→v3,再由(1,2)步竞争图的定义,vn-1v1∈E(C1,2(D)),vn-1v2∈E(C1,2(D))。 当n是奇数时,哈密尔顿圈vn-1v1v0v3v5v7…vn-2 vn-3vn-5…v4v2vn-1是C1,2(D)的子图,所以C1,2(D)中存在哈密尔顿圈。 当n是偶数时,哈密尔顿圈vn-1v1v0v3v5v7… vn-3vn-2vn-4…v4v2vn-1是C1,2(D)的子图,所以C1,2(D)中存在哈密尔顿圈。 定理6 若n(n≥5)阶强连通圆有向图D中仅有2个下标相邻的顶点同时是割点且有一个割点的出度大于2,其余下标不相邻的割点出度也大于2,则C1,2(D)中存在哈密尔顿圈。 证明(1) 设va1-1,va1是n(n≥5)阶强连通圆有向图D中两个下标不相邻的割点。存在以下两种情形: 1) 连续的顶点集{va1,va1+1,va1+2,…,va1+b1}构成的扁条B1是D的子有向图。因为d+(va1)>2,所以b1≥3。由引理6,得: 当b1=3时,C1,2(B1)为K3∪{va1+b1}; 2) 记a1+b1=a2,连续的顶点集{va2,va2+1,va2+2,…,va2+b2}构成的扁条B2也是D的子有向图。因为d+(va2)>2,所以b2≥3。由引理6,得: 当b2=3时,C1,2(B2)为K3∪{va2+b2}; ∪{va2+b2}。 重复上述过程,记ar-1+br-1=ar,连续的顶点集{var,var+1,var+2,…,var+br}构成的扁条Br也是D的子有向图,此时var+br=var-1。因为d+(var)>2,所以b2≥3。由引理6,得: 当br=3时,C1,2(Br)为K3∪{var+br}; ∪{var+br}。 (2) 在圆的有向图D中,因为d+(vai)>3(i=1,2,…,r-1),所以有以下两种情形: 1) 当bi=3(i=1,2,…,r-1)时,因为vai→vai+bi→vai+bi+3,vai+bi+1→vai+bi+3,vai+bi+2→vai+bi+3。 由(1,2)步竞争图的定义,vaivai+bi+1∈E(C1,2(D)),vaivai+bi+2∈E(C1,2(D))。同理,有vai+1vai+bi+1,vai+1vai+bi+2,vai+2vai+bi+1vai+2vai+bi+2∈E(C1,2(D))。根据(1),vai+1vaivai+bi+1vai+bi,vai+2vai+bi+2分别是C1,2(D)中的路。 2) 当br≥4(i=1,2,…,r-1)时,因vai+bi-2→vai+bi→vai+bi+3,vai+bi+1→vai+bi+3,vai+bi+2→vai+bi+3。 由(1,2)步竞争图的定义,vai+bi-2vai+bi+1,vai+bi-2vai+bi+2∈E(C1,2(D)),同理,有vai+bi-1vai+bi+1,vai+bi-1vai+bi+2∈E(C1,2(D))。 根据(1),vai+1vaivai+3vai+5…vai+bi-1vai+bi+1vai+bi,vai+2vai+4…vai+bi-2vai+bi+2(bi为偶数)或者vai+2vai+4… vai+bi-1vai+bi+2(bi为奇数)分别是C1,2(D)中的两条路。 把上述的2(r-2)条路按照事先拍好的顺序连起来构成C1,2(D)中的两条不相交的路,记作P1,P2,其中P1的起点终点分别为va1+1,var;P2的起点终点分别为va1+2,var+2。 (3) 在圆有向图D中,存在以下两种情形: 1) 因为d+(va1)>3,所以有va1 -1→va1→va1 +3,va1 +1→va1 +3va1 +2→va1 +3由(1,2)步竞争图的定义,va1-1va1+1∈E(C1,2(D)),va1-2va1+2∈E(C1,2(D))通过va1-1把(2)中的两条路P1,P2连接起来构成一条新的路,记为P,其中P的起点终点分别是var,va1+2。 2) 因为d+(var)>3,所以br≥3。 当br=3时,因为C1,2(Br)为K3∪{var+br},所以varvar+2∈E(C1,2(D)),则路P起点终点相连,构成C1,2(D)中的一个哈密尔顿圈。 ∪{var+br},所以varvar+3var+5var+7…var+br-3var+br-1var+br-2var+br-4…var+4var+2(br为偶数) 或者varvar+3var+5var+7… var+br-2var+br-1var+br-3var+br-5…var+4var+2(br为奇数)是C1,2(D)中的路,与路P的起点终点相连构成C1,2(D)中的哈密尔顿圈。 以上研究了所有的n阶(n≥5)的强连通圆有向图D中(1,2)步竞争图中存在哈密尔顿圈的条件,非强连通的圆有向图D中(1,2)步竞争图中显然不存在哈密尔顿圈,因为D中存在出度为0的顶点或孤立点,这些点不与任何其他顶点构成(1,2)步竞争,阶n小于5的强连通圆有向图的(1,2)步竞争图可以通过画图得到,它的(1,2)步竞争图中也不存在哈密尔顿圈。 [1] UTTONR D, BRIGHAM R. A Characterization of Competition Graphs[J]. Discrete Appl Math, 1983,6(3): 315-317 [2] LUNDGREN J, MAYBEE S. A character ization of Fraphs of Competition Numberm[J]. Discrete Applied Mathematics New York, 1983,6(3), 319-322 [3] KIMH, CHO S, NAM Y. The M-step Competition Graph of a Digraph[J]. Discrete Appl, Math,2000,105: 115-127 [4] MERZ S , LUNDGREN R K, REID B. The Domination and Competition Graphs of a Tournament[J]. Graph Theory,1998,29(2):103-110 [5] FACTOR K, MERZ S. The (1,2)Step Competition Graph of aTournament[J]. Discrete Appl Math,2011,59(2-3): 100-103 [6] BONDY J, MURTY U. Graph Theory With Application[M]. New York: Springer, 2007 [7] BANG-JENSEN J, GUTING. Digraphs: Theory,Algorithms and Applications in: Spring Monographs in Mathematics[M]. London: Spring-Verlag,2001 [8] BANG-JENSEN J,HUANG J.Decomposing Locally Semicomplete Digraphs into Strong Spanning Subdigraphs[J].Journal of ComBina-torial Theory,Series B,2012,102(3): 701-714 [9] BANG-JENSEN J, HUANG J. Arc-Disjoint In-and Out-Branchings With the Same Root in Locally Semicomplete Digraphs[J]. Journal of Graph Theory, 2014,77(4): 278-298 The (1,2) Step Competition Graph of Round Digraph Contains Hamiltonian Cycles CUIJian1,YEWang2 (1.Basic Medicine Department, Fenyang College, Shanxi Medical University, Shanxi Luliang 032200, China; 2. School of Mathematical Science, Shanxi University, Shanxi Taiyuan 030000, China) With regard to the (1,2) step competition graph structure of round digraph, this paper puts forward whether the (1,2) step competition graph of round directed graph contains Hamilton cycle, and through special to general method, receives the following conclusion: Hamilton cycle is contained in order of strongly connected directed graph of the (1,2)step competition graph, and the rest of the situation of round digraph (1,2)step competition graphs does not contain Hamilton cycle. round digraph; (1,2)step competition graph; Hamilton cycle O157.5 A 2017-04-12; 2017-05-30. 崔建(1988-) ,男,山西吕梁人,硕士,从事图论和机器学习研究。 责任编辑:代小红3 存在哈密尔顿圈的条件分析之二
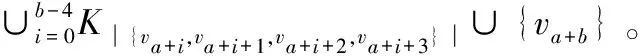

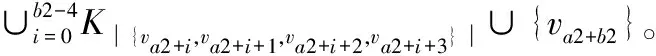

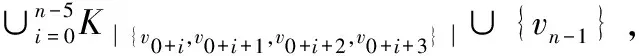

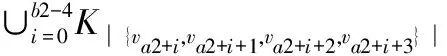

4 结 论



