水泥净浆单轴受压力学性能试验与分析

解恒燕，陈斌

（黑龙江八一农垦大学工程学院，大庆 163319）

水泥净浆单轴受压力学性能试验与分析

解恒燕，陈斌

（黑龙江八一农垦大学工程学院，大庆 163319）

为得到简单配比的水泥净浆单轴受压力学性能，进行了2种配合比的水泥净浆试件试验，给出了试验现象与破坏过程，得到了水泥净浆试件力学性能指标。分析了弹性模量变化规律，给出了以水泥净浆棱柱体抗压强度为基础的弹性模量计算公式。分析了水泥净浆单轴受压应力-应变曲线上升段变化规律，采用混凝土规范公式拟合得到了水泥净浆单抽受压应力-应变曲线上升段计算公式，给出了曲线参数取值。给出了通过强度计算得到水泥净浆弹性模量及应力-应变曲线上升段的计算方法，为工程实践及采用水泥净浆进行分析提供基础素材。

水泥净浆；单轴受压；力学性能；弹性模量；应力-应变曲线

单栋塑料大棚轻钢温室结构广泛应用于我国东北和华北的大部分地区。现有轻钢温室结构存在抵抗暴风、暴雪能力差、稳定性差的缺点。针对这一现状，提出采用切实可行的方法加固现有轻钢温室的思想，对上弦受压钢管灌浆是加固方法之一。由于钢管截面较小，因此采用的灌浆料主要为水泥净浆。在采用分析软件对灌浆钢管进行分析时，需要输入水泥净浆的基本力学性能指标，如强度、弹性模量、峰值应变及本构模型等。在查阅文献过程中，发现多数研究成果都是针对特殊的水泥基灌浆材料，而针对于简单配制的水泥净浆研究反而较少，这类材料的基本性能指标较难得到。如简单照抄混凝土的相关指标，又很难信服。针对这种情况，研究了由水泥、水、外加剂为膨胀剂和减水剂所组成的简单配比的水泥净浆体的基本性能，为后续研究提供基础。

1 水泥净浆试件制作

根据灌浆所需的流动性，试验设计了2组不同配合比的水泥净浆，如表1所示，表中配比均为质量比。试验用水泥为大庆市同源水泥厂生产的P·O 42.5普通硅酸盐水泥，膨胀剂和减水剂均为哈尔滨铁路混凝土外加剂厂生产。

表1 水泥净浆配合比Table 1Mix proportion of cement paste

试验所用水泥净浆试件编号如表2所示。

表2 水泥净浆试件编号Table 2The number of cement paste specimen

仿照建筑砂浆的制作方法，同时为了比较基层吸水性对水泥净浆强度的影响，每组配合比分别制作无底模和有底模2种试件[1]。无底模试件置于吸水性较强的红砖上。为了便于拆模，在红砖表面与试件中间放置一层吸水纸。试件尺寸为：立方体70.7× 70.7×70.7 mm，棱柱体70.7×70.7×210 mm，圆柱体d× h=70.7×210 mm。每组3个试件，在标准养护条件下养护7 d后进行试验。

依据JGJ/T70-2009《建筑砂浆基本性能试验方法》[2]，水泥净浆试件的制备程序为：将称量好的P·O 42.5普通硅酸盐水泥、UEA膨胀剂和FDN减水剂倒入搅拌台，采用人工干拌3 min；在搅拌过程中缓缓加入称量好的水，湿拌5 min；将拌合物注入钢模，使用长度400 mm、直径16 mm的钢棒进行振捣，重点对模具4个角部进行多次振捣，每个部位振捣不少于30次。振捣结束后将试件静置20 min，发现试件上表面有少量水分离出来，如图1所示。经测试，首次静置分离水高度平均为6 mm左右。此时需将水缓缓倾倒出来，填入净浆至试模高度，进行补浆并振捣。静置数分钟后，发现仍有水分离现象，再进行补浆。试件从开始制作到完成，需要5～6次补浆，直至试件制作达到设计高度且不再有水分离出来为止。大约每个试件耗时3 h。试件制作完成后，在20±5℃温度环境下静置24 h，然后编号、拆模，将试件立即放入温度为20±2℃，相对湿度为95%以上的标准养护室中养护，7 d后进行试验[3]。

2 试验测试装置

在棱柱体试件两侧面中部各沿试件长度方向粘贴了2片纸基电阻应变片，用以测量试件纵向应变[4]。在另外两个侧面各沿垂直于试件长度方向粘贴了2片应变片，用以测量试件横向应变，如图2所示。在沿圆柱体试件长度方向及垂直方向各粘贴了1片应变片，如图3所示。采用江苏东华测试技术股份有限公司生产的DH-3818N静态应变测试仪量测试件的应变。应变片尺寸为：有效栅宽×栅长=5×40 mm。

图1 水泥净浆表面的水分离现象Fig.1Water seperation on the surface of cement paste specimen

图2棱柱体试件应变片布置Fig.2Strain gage on prism specimen

图3 圆柱体试件应变片布置Fig.3Strain gage on cylinder specimen

水泥净浆试件在万能试验机上进行逐级加载，应变测试系统与应力同步采集。依据《建筑砂浆基本性能试验方法》JGJ/T70-2009[2]中的试验方法对试件进行加载。加载速率为0.3～0.5 MPa·s-1，匀速加载。同时控制试件的变形速率不大于10 με·ε-1，即每秒10个微应变[5]。当加载速率与变形速率发生矛盾时，以变形速度控制为准。试验加载及采集装置如图4所示。

图4 试验加载及采集装置Fig.4Loading and collecting devices

3 试验现象

水泥净浆立方体试件与普通混凝土立方体试件破坏过程相似。在加载达到极限荷载的30%时，立方体试件角部首先产生微小裂缝，随着加载持续，可听到试件发出连续的脆性响声。在加载达到极限荷载的60%时，试件表面可见竖向裂缝。在加载达到极限荷载的80%时，体试件开始产生大量的竖向裂缝，较大的碎片从试件表面剥落分离，且随着加载持续，剥落不断向试件内部发展。卸载后，剥去表面被压酥的净浆碎片，破坏后的试件呈双角锥状[6]，如图5所示。

图5 卸载后的立方体试件Fig.5Cube specimen after unloading

棱柱体试件在加载达到极限荷载的30%时，试件发出轻微的响声，可观察到在试件表面出现沿纵向的细小裂缝。随着加载持续，纵向裂缝逐渐延长，并伴有角部表面脱落现象。在加载达到极限荷载的70%时，有持续的响声发出，纵向裂缝逐渐贯通同时有多条纵向裂缝产生，棱柱体角部脱落明显。在加载达到极限荷载的90%时，数条纵向贯通裂缝逐渐变宽并发生分离。试件破坏的瞬间，可听到巨大的响声。破坏后的棱柱体试件如图6所示。

圆柱体试件在加载初期，试验现象与棱柱体试件相似。加载后期破坏现象比棱柱体严重。在加载达到极限荷载的30%时，开始出现有轻微的响声，与棱柱体试件不同的是，此时可以明显地观察到圆柱体试件周围都有纵向长裂缝产生。在加载达到极限荷载的60%时，试件持续地发出轻微响声，此时外观裂缝并无明显变化。在加载达到极限荷载的80%时，试件上下表面与压力机接触部分发生破坏，纵向裂缝逐渐延长，圆柱体表面有脱落。试件接近达承载能力极限时，圆柱体表面开始快速并大面积地脱落，达到最终破坏时，圆柱体试件会有较大响声出现，最终破坏呈压溃状态，如图7所示。

4 试验结果及分析

4.1 物理力学性能指标

得到2组不同配合比的水泥净浆试件立方体抗压强度fcu、棱柱体抗压强度fc、圆柱体抗压强度f′c及弹性模量E等力学性能指标如表3所示。

图6 受压破坏的棱柱体试件Fig.6Prism specimen after compression failure

图7 受压破坏的圆柱体试件Fig.7Cyclinder specimen after compression failure

表3 水泥净浆试件力学性能指标Table 3Mechanical property index of cement paste specimen

由表3可见，无底模试件比有底模试件强度高。证明基层吸水性对水泥净浆强度存在影响。水泥净浆棱柱体抗压强度与立方体抗压强度比值平均为：fc/fcu=0.936，圆柱体抗压强度与立方体抗压强度比值平均为：f′c/fcu=0.388。可见水泥净浆强度换算规律不同于普通混凝土，fc/fcu比混凝土高，f′c/fcu比混凝土低。分析其原因，混凝土内部是多层次的二项复合结构，存在初始微裂缝。而水泥净浆体由于没有砂、石等粗细骨料，内部结构相对均匀，如图8所示。因此，在相同荷载作用下，水泥净浆体与普通混凝土内部微裂缝产生、扩展及失稳过程破坏可能不同，因此水泥净浆强度规律不能简单照抄混凝土。

4.2 弹性模量

试验测得水泥净浆试件弹性模量如表2所示。《混凝土结构设计规范》（GB 50010-2010）[8]中，普通混凝土的弹性模量Ec以其强度等级值（fcu，k为代表值）按式（1）计算：

图8 水泥净浆试件内部结构Fig.8Inner structure of cement paste specimen

将表2中试验得到的水泥净浆弹性模量仿照上式进行计算，强度按照试验得到的fcu带入式（1），可得到水泥净浆弹性模量试验值与按照规范的计算值随强度的变化试验点如图9所示。

图9 水泥净浆弹性模量计算值与实验值分布Fig.9Distribution of calculated and tested elasticitymodulus of cement paste

由图9可见，水泥净浆弹性模量比按照“规范”计算得到的混凝土弹性模量小。由于净浆体内部没有粗骨料，因此在相同荷载作用下，水泥净浆体比普通混凝土变形大，弹性模量小。由图9可见，水泥净浆体弹性模量随着强度的提高而提高。强度和弹性模量是水泥石内部组成及微观结构特征在不同方面对其力学性能的表现[9]。当已知水泥净浆体强度，需要估算其弹性模量时，根据文献[9-10]提出的方法，以试验测得的棱柱体或圆柱体抗压强度为横坐标，以水泥净浆试件弹性模量为纵坐标，得到水泥净浆试件弹性模量随强度的变化有效试验点分布及拟合曲线如图10所示。

图10 水泥净浆试件弹性模量随强度变化分布Fig.10Distribution of elasticity modulus of cement paste with the change of strength

由图10可见，试验点分布比较离散，因此采用式（2）进行弹性模量计算，也只能是大致的推算。试验试件个数有限，只有增大样本数目，才能得到更精确的计算结果。

根据试验结果，水泥净浆的泊松比可按照混凝土泊松比取值，即vc=0.2。

图10中实线为拟合曲线，其方程为式（2）：

4.3 水泥净浆试件应力—应变关系

试验得到了水泥净浆试件上升段在各级荷载下的应力及应变数据。按照（GB50010-2010）《混凝土结构设计规范》附录C[8]给出的混凝土单轴受压的应力-应变关系上升段进行数据拟合，拟合公式为：

式中fc，r为混凝土单轴抗压强度，εc，r为与fc，r相对应的混凝土峰值压应变，dc为混凝土单轴受压损伤演化参数。

拟合公式中的数据fc，r、εc，r及Ec均采用本次棱柱体试件的试验平均值。以1-2-P及2-2-P为例，试验实测应力-应变试验点分布及按照（3）式拟合曲线如图11及图12所示。为了方便比较，图中坐标值为归一值，即横坐标ε/εc，r为应变与峰值应力对应的压应变的比值，纵坐标σ/fc，r为应力与峰值应力的比值。

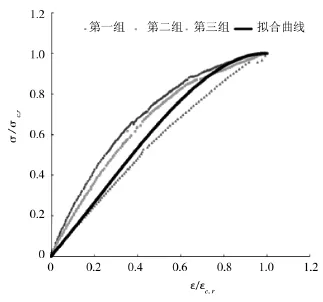
图11 试件1-2-P应力-应变试验点分布及拟合曲线Fig.11Test points and the fitting curve of stress-strainfor specimen 1-2-P

图12 试件2-2-P应力-应变试验点分布及拟合曲线Fig.12Test points and the fitting curve of stress-strain for specimen 2-2-P

试验水泥净浆fc在30～45 N·mm-2之间。根据试验测得的各试件fc，r及对应的εc，r，拟合得到水泥净浆单轴受压应力—应变曲线上升段峰值应力fc，r与峰值应变εc，r大致取值如表4所示。

表4 水泥净浆单轴受压应力—应变曲线参数取值Table 4Parameters in stress-stain curve of cement paste subjected to uniaxial compression

从以上分析可见，虽然水泥净浆与混凝土应力-应变关系不同，但仍可采用混凝土规范给出的应力-应变模型来分析水泥净浆的应力-应变关系。

5 结语

进行了2种配合比的水泥净浆试件试验，得到了水泥净浆试件力学性能指标，给出了以水泥净浆棱柱体抗压强度为基础的弹性模量计算公式，采用混凝土规范公式拟合得到了水泥净浆单轴受压应力-应变曲线上升段计算公式，给出了曲线参数取值。为水泥净浆进行后续研究提供了基础。同时水泥净浆试件样本数目少，试件尺寸偏小，试验方法与“规范”不完全一致，应力-应变曲线也只得到了上升段，这些都是试验的不足之处。尚待对水泥净浆的力学性能进行深入研究，以更好地为工程实践及模拟分析服务。

［1］孙永民，胡长明，宋方方.不同底模对砂浆强度的影响［J］.施工技术，2012，41（376）：58-61.

［2］JGJ/T70-2009.建筑砂浆基本性能试验方法［S］.北京：中国建筑工业出版社，2009.

［3］陈旭阳.浅谈标准养护室温湿度控制的设计［J］.中国纤检，2010，15（8）：83.

［4］王钧，叶焕军，张野.不同粉煤灰掺量下自密实混凝土的试验研究［J］.森林工程，2010，26（5）：72-75.

［5］袁自立，王立霞，黑君淼，等.塑性混凝土弹性模量试验方法研究［J］.人民黄河，2013，35（8）：84-90.

［6］解恒燕，郑鑫，杨忠国.自密实混凝土基本力学性能［J］.低温建筑技术，2009，132（6）：10-12.

［7］GB/T50081-2002.普通混凝土力学性能试验方法标准［S］.北京：中国建筑工业出版社，2002.

［8］GB50010-2010.混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［9］张景富，林波，王珣，等.单轴应力条件下水泥石强度与弹性模量的关系［J］.科学技术与工程，2010，10（21）：5249-5256.

［10］吕雪源，王英，符程俊，郑文忠.活性粉末混凝土基本力学性能指标取值［J］.哈尔滨工业大学学报，2014，46（10）：1-9.

Experiment and Analysis on Mechanical Properties of Cement Grout Subjected to Uniaxial Compression

Xie Hengyan，Chen Bin
（College of Engineering，Heilongjiang Bayi Agriculture University，Daqing 163319）

In order to get the mechanical properties of simple cement paste subjected to uniaxial compression，2 mix proportion cement paste were tested.Phenomena in the experiment and destruction process were described，and the mechanical property index of cement paste was given.Law of elasticity modulus was analyzed，and the calculation formula of elasticity modulus of cement paste based on the prism compression strength was obtained.The law of ascending stage in stress-strain curve of cement paste subjected to uniaxial compression was analyzed.The calculation formula of the ascending stage was gotten by curve fitting conforming to the formula in concrete design code.The parameters in the curve were given.The calculation of elasticity modulus of cement paste and the ascending stage of the stress-strain curve were given in this paper，which would provide basis for actual engineering practice and analysis using software.

cement paste；uniaxial compression；mechanical property；elasticity modulus；stress-strain curve

TU392.2

A

1002-2090（2017）01-0094-06

2015-11-25

黑龙江省教育厅新世纪优秀人才支持计划项目（20102305120003）；黑龙江省普通高等学校青年学术骨干支持计划项目（1155G37）；黑龙江八一农垦大学引进人才科研启动计划项（XYB2012-15）。

解恒燕（1973-），女，副教授，哈尔滨工业大学毕业，现主要从事结构工程、农业生物环境与能源工程等方面的研究工作。