通货膨胀水平、股票市值与中国国债利率期限结构

巴曙松+袁佳+廖慧

摘 要：本文选取2007年1月—2016年6月中国国债即期收益率数据，利用动態Nelson-Siegel模型构造反映国债利率期限结构的水平、斜率和曲率因子，并运用Johansen协整检验、VEC模型等方法考察通货膨胀水平、股票市值与利率期限结构间的行为特征，研究发现：通过Nelson-Siegel模型构造的结构因子体现出利率期限结构的特征；通货膨胀率、股票市值与国债利率期限结构的水平、斜率因子之间存在长期的协整关系，但是通货膨胀水平和股票市值变动对水平因子无显著影响，反映出货币政策向债券市场传导的效率有待完善；长期看来，通货膨胀水平和股票市值均在缩小斜率因子方面效果显著。此外，斜率因子可以预测出通货膨胀水平的变化，为制定和实施货币政策提供前瞻性信息。

关键词：利率期限结构；通货膨胀率；股票市值；动态Nelson-Siegel模型

中图分类号：F832.5 文献标识码：A 文章编号：1674-2265（2017）01-0003-08

一、引言

2016年6月15日，中国人民银行官网发布了国债等债券收益率曲线，旨在提升国内外市场主体对国债收益率曲线的关注和认可，完善国债收益率曲线的基准性，推动人民币国际化进程。债券收益率曲线也称为利率期限结构，表示不存在违约风险时零息债券到期时间与到期收益率的关系。从微观层面看，利率期限结构是金融市场基准利率曲线，反映市场资金供需成本，引导资源的配置，成为资产定价、金融产品设计、保值和风险管理的基础；从宏观层面看，收益率曲线是基于对未来预期而定，其中蕴含了反映市场参与者对经济运行状况的预期和货币当局宏观调控目标等有效信息，宏观经济和金融市场的波动会对收益率曲线产生影响。中国宏观调控从数量型转向价格型的过程中，货币政策传导机制主要通过银行体系和债券市场传导（马骏等，2016）。在债券市场中，货币政策和其他宏观变量通过改变收益率曲线形状（水平、斜率和曲率），改变当前融资成本或是影响市场对经济的预期，进而影响实体经济。在中国货币政策转型的背景下，分析宏观经济和金融市场对利率期限结构的影响效果，可以有的放矢地进行改革，提高货币政策传导的有效性。

通货膨胀水平是观测宏观经济运行状况的重要指标，也是与债券市场联系极为紧密的变量。在利率市场化经济中，货币当局基于其通货膨胀、产出水平等指标，调整利率水平，进而实现其经济目标。股票市场和债券市场是中国金融市场非常重要的组成部分，它们之间存在着相互替代、相互影响的关系，股票市值则直观地反映了股票市场价值。在当前经济形势较复杂、货币政策转型、政策措施需协调配合的情况下，央行需要更多的前瞻性信息来优化货币政策的调控措施，我们希望通过对中国数据的实证研究回答通货膨胀水平、股票市值对中国国债利率期限结构的影响。本文结构安排如下：第二部分讨论通货膨胀水平、股票市场与国债利率期限结构关联性的理论文献；第三部分采用Nelson-Siegel参数模型估计中国利率期限结构，并分析其特征；第四部分和第五部分实证分析通货膨胀水平、股票市值对国债利率期限结构的影响及利率期限结构对通货膨胀水平的预测效果；第六部分是结论性评述。

二、相关文献述评

（一）利率期限结构理论研究

国内外对国债利率期限结构的研究重心逐渐由纯预期理论（Fisher，1930；Keynes，1930；Hicks，1953）、市场分割理论（Culbertson，1957）和流动性升水理论（Hicks，1946）等为代表的传统理论研究，转向以对利率期限结构的数据拟合与预测为主的定量模型为代表的现代利率期限结构理论。现代利率期限结构理论主要分为两类：一类是基于金融学的无套利和市场均衡构建的仿射模型（Hull和White，1990；Vasicek，1977；Duffie和Kan，1996等）；另一类是基于数据的统计特征构建的统计参数模型（Nelson和Siegel，1987；Diebold和Li，2006等）。第一类模型主要是从微观角度研究利率期限结构特征，忽略了宏观经济运行产生的影响，且在真实市场数据拟合和预测中效果欠佳，对样本数据的依赖性较强，因此这种方法存在争议（Duffee，2002）。第二类参数模型中Nelson-Siegel模型虽是从统计意义上建模，但是模型具有较强的经济学含义（Christensen等，2007），通过对收益率曲线降维，分解出水平因子、斜率因子和曲率因子，有效地刻画利率期限结构对宏观经济变量变化的预期及其自身的内生周期性特征（贺畅达，2012；丁志国和徐德财等，2014）。目前Nelson-Siegel模型已被世界上大多数中央银行，如美国、英国、意大利、比利时等运用于对国债利率期限结构的估计（BIS，2005），同时在金融实践中也得到了广泛运用。水平因子和长期利率高度相关，斜率因子与长短期利差走势也表现出一致性，水平因子比斜率因子和曲率因子波动幅度小，且偏离均值的程度也较小（Diebold和Li，2006；何晓群和王彦飞，2014）。一些实证检验结果显示，Nelson-Siegel模型同时适用于中国国债利率期限结构动态特征的拟合与预测（余文龙和王安兴，2010；赵晶和张洋等，2014）。

（二）通货膨胀水平与利率期限结构的关系

利率期限结构为测度和判断宏观经济决策及其效果提供了重要信息，同时也为预测经济周期和通货膨胀水平提供了有效参考。Fisher方程中将名义利率分解为实际利率和预期通货膨胀率，证明了通货膨胀与利率期限结构的相关性。有关利率期限结构与通货膨胀率的相互关系研究主要集中在两方面：一方面是研究利率期限结构对通货膨胀的预测能力，另一方面是研究通货膨胀率对收益率曲线的影响效果。Estella和Mishkin（1997）通过对欧美收益率曲线的研究，发现收益率曲线对真实经济活动及通货膨胀率有显著的预测能力。Blundell等（1990）对六个OECD国家实证研究发现，短端的利率期限结构对通货膨胀有一定的预测能力。李宏瑾、钟正生、李晓嘉（2010）发现中国短期利率结构包含了未来通货膨胀变动的信息，可判断未来通货膨胀的走势。张旭和文忠桥（2014）以Nelson-Siegel模型估计的国债市场利率期限结构因子序列为研究样本，发现实体经济和物价因素是造成利率期限结构变化的主要原因。石柱鲜等（2008）研究1996—2006年数据发现通货膨胀冲击对不同期限利差产生正向影响。Burre（2010）建立新凯恩斯模型，研究结果显示通货膨胀波动率对收益率曲线的因子产生冲击。

（三）股票市场与利率期限结构的关系

在有效的金融市场中，投資者会根据分散风险的投资原则进行组合投资，研究股票市场与利率期限结构的关系不仅能为管理者配置资产提供参考，同时也为金融监管提供有价值的信息。Ilmanen（2003）研究美国债券和股票收益率的相关关系时发现，二者在不同时期的相关性不同，在20世纪30年代前期和50年代末期二者呈现出负相关。负相关表明投资者从债券市场的上升中获利弥补股票市场的亏损。Campbell等（2013）对美国名义债券收益率和股票收益的关系进行研究，发现在1960—1965年期间，股票收益率和债券收益率正相关，在2000—2009年，股票收益率和债券收益率负相关。曾志坚和江洲（2007）通过VAR模型发现中国股票和债券市场收益率存在长期影响。王茵田和文志瑛（2010）通过实证分析发现，中国股票市场和债券市场流动性之间存在一定的因果关系。郑振龙和陈志英（2011）基于A股综合市场收益率和中信全债指数收益率数据，利用DCC模型分析中国股票市场和债券市场收益率的动态相关性，发现股票和债券的相关系数是时变的，且大部分时期呈现正相关。汪军红（2006）发现股票市场成交量对债券市场的截距有显著的正效应影响，表明中国股票市场和债券市场存在较强的替代关系。

通过梳理相关文献发现，目前国内学者主要是通过研究宏观经济变量对国债利率期限结构的影响，且囿于选择的样本区间和技术处理手段不同，宏观经济变量对国债利率期限结构的影响结论也有所差别。虽然一些学者对股票和债券收益率的相关性进行探讨，但结论莫衷一是。鲜有学者考虑股票市值等金融市场因素是否会引起利率期限结构的变化。因此，本文选取通货膨胀率和股票市值作为影响利率期限结构的因素进行考察，研究其是否会对国债利率期限结构产生影响。

三、国债利率期限结构特征分析

Nelson和Siegel（1987）利用参数化拟合技术对利率期限结构进行估计，得到远期利率的经验方程，并将其视为由一个常数项加上一个Laguerre函数，根据即期利率同远期利率之间的关系积分得到：

[y（τ）t=β1t+β2t1-exp（-λtτ）λtτ+β3t1-exp（-λtτ）λtτ-exp（-λtτ）]

模型中[y（τ）t]为[t]时刻期限为[τ]的即期收益率，[λt]、[β1t]、[β2t]、[β3t]为利率期限结构模型的4个参数，具有明确的经济意义。根据模型构造形式可以看出，当期限[τ]无穷大时，[limτ→∞y（τ）t=β1t]，因此[β1t]表示长期利率水平，也称作的水平因子（[Lt]）；[β2t]的因子载荷[1-exp（-λtτ）λtτ]是从1迅速衰减到0的函数，当期限较短时，[β2t]对利率的影响较大，随着期限的延长，[β2t]的影响越来越弱，[β2t]代表着短期因素的变化。由于[-β2t=limτ→∞y（τ）t]

[-limτ→0y（τ）t]，因此[-β2t]可视为长短期利差，表示收益率曲线的斜率，称为斜率因子（[St]）。[β3t]的因子载荷[1-exp（-λtτ）λtτ-exp（-λtτ）]随着时间的延长，是一个从0增大最后又降至0的过程，在中期达到最大值。因此，[β3t]可以视为中期因素，决定曲线中部的陡峭程度，也称为曲率因子（[Ct]）。

（一）数据介绍

2006年3月，中央国债登记结算有限责任公司经过深入研究，利用Hermite模型编制了债券收益率曲线，具有光滑性、灵活性、稳定性三方面优势，适应中国债券市场的情况（马骏等，2016）。由于日度或周度的宏观经济变量数据难以获得，且收益率曲线特征不稳定，季度数据或年度数据时间跨度过大。因此，本文数据采用从2007年1月到2016年6月中债国债1个月、1年、2年、3年、5年、8年、10年、15年、20年共9种类型的月度即期收益率（由月末值衡量），数据来自于万得数据库。

（二）参数估计

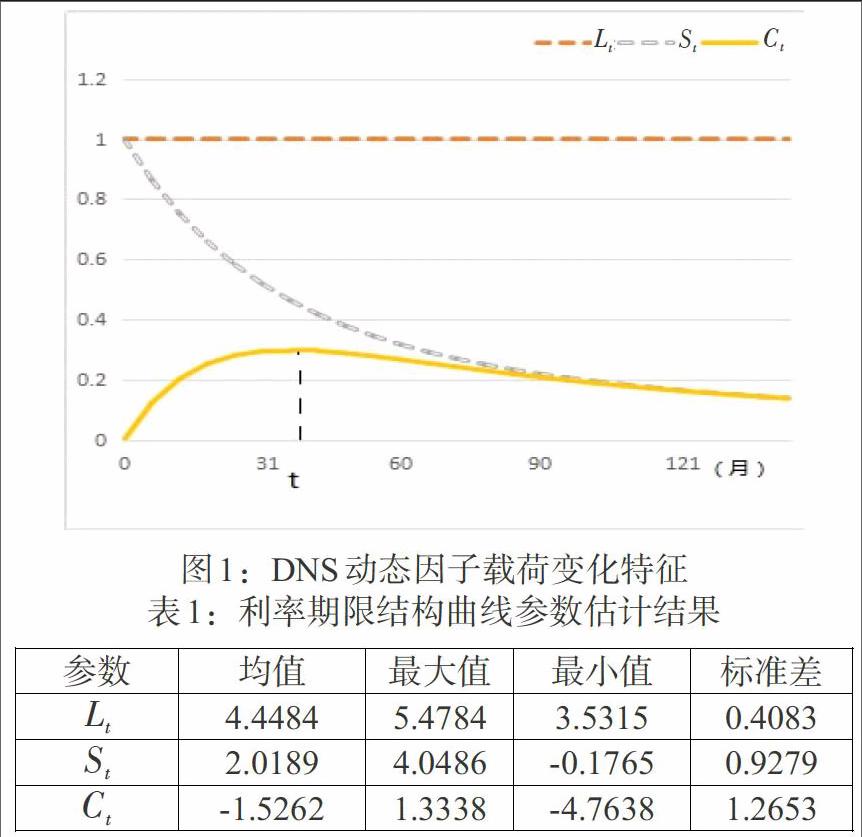
动态Nelson-Siegel模型（DNS模型）通过确定参数[λ]，保证了其他参数的稳定性。[Ct]是曲率因子，因此[Ct]的参数应当在中期达到最大。中国的中期债券期限一般是2到5年。设定期限[τ]的范围为[24，60]，当[τ]=36，参数[λ]=0.05，此时拟合残差平方和最小。本文借助于R软件进行实证研究，采用Nelson-Siegel模型来实现曲线拟合最优并估计得到参数集[[Lt]，[St]，[Ct]]。水平因子、斜率因子、曲率因子的因子载荷随到期时间的变化情况如图1所示。

采用Nelson-Siegel模型来实现曲线拟合最优并估计得到114个参数集的统计特征如表1。

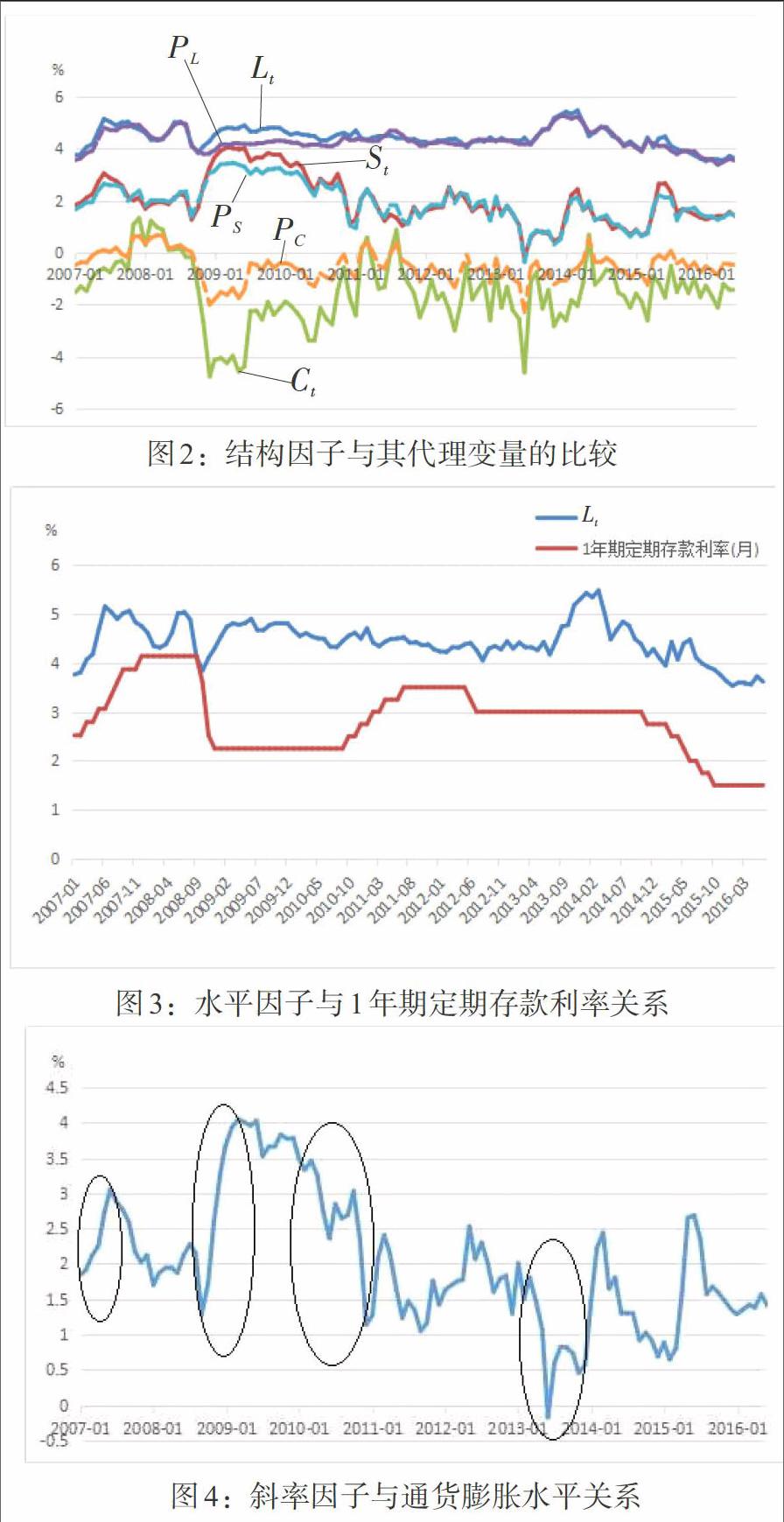
样本中国债收益率期限最长的是20年，最短的为1个月，中期为3年。因此水平因子（[Lt]）的代理变量为20年期的国债收益率，即PL=[y240]；斜率因子（[St]）的代理变量为长期利率与短期利率之差，即PS=[y240-y1]；曲率因子（[Ct]）的代理变量为PC=[2y36-y1-y240]。估计的结构因子与经验代理变量的关系见图2。

结构因子的时间序列与利率期限结构代理变量的走势具有明显的一致性。水平因子与其代理变量相关系数为0.871；斜率因子与其代理变量的相关系数为0.976；曲率因子与其代理变量之间的走势相同，相关系数为0.956。数据结果进一步表明3个结构因子较好地解释了债券市场的长期、短期和中期效应。结构因子的波动幅度明显大于其代理变量。

水平因子解释了长期利率水平，走势较为平稳。根据预期假说理论，长期利率的变化是基于当前和未来短期利率共同作用。由于远期利率的反应会随时间变化而趋于稳定，长期利率主要由市场供求状况决定。样本区间内水平因子与1年期定期存款利率的相关性为0.4136（见图3），中国长期施行的利率管制也会对水平因子产生一定影响。此外，受供求关系影响，长期国债收益率还与国债发行量等有一定关系。

根据费雪效应方程，名义利率等于实际利率和预期通货膨胀率之和。斜率因子体現了长短期利差的变化，反映出对未来利率和通货膨胀预期的变动。2007年1—9月通货膨胀水平攀升，为防止经济转向过热，央行曾先后5次提高利率，短期利率急剧上行，利差收窄，斜率因子变小。2008年9月，雷曼倒闭导致金融危机恶化后，通货膨胀率逐步下降，中国央行于当年10月连续两次降息和一次降准，从2008年11月起短期利率显著下行，长期利率下降幅度较小，导致长短期利差变大。在2010年，为缓解金融危机对经济紧缩的影响，央行实行宽松的货币政策，投放大量的货币，导致通货膨胀压力增加，利差也迅速缩小。2013年上半年市场资金宽松，长期利率略有下行，短期利率平稳。2013年6月，资金市场发生钱荒，短端收益率迅速上行，长端收益率也随之上行。短期收益率上行程度更大，使得长短利差迅速收窄（见图4）。至此，可以推测通货膨胀率与斜率因子存在一定的关系。2008年的全球金融危机对国债期限结构的曲率因子产生显著影响，而传统的代理变量并未反映出这一变化。传统的代理变量还容易受异常值影响，未能充分表现利率期限结构所蕴含的信息。通过动态Nelson-Siegel模型估计出结构因子明显地呈现出宏观经济变化对利率期限结构的影响效果。

四、通货膨胀水平、股票市值对国债利率期限结构的影响分析

为分析经济因素冲击如何影响收益率曲线的特征参数，进而分析利率期限结构与经济变量之间的相互关系，VAR估计是一种较为直观有效的研究方法。由于[Ct]与宏观经济变量的相关性较弱，经济意义不明显，且水平因子和斜率因子基本解释了期限结构的主要变动（Litterman和Scheinkman，1991；康书隆和王志强，2010；陈浪南和郑衡亮，2015），同时曲率因子具有内生周期性（丁志国和徐德财等，2014），故本文将不对曲率因子进行分析。

（一）单位根检验

通过Nelson-Siegel模型分解的水平因子（[Lt]）、斜率因子（[St]）有效地表示出长期因素和长短期利差因素。通货膨胀率用居民消费价格指数（CPI）以2006年各月为基期（=100）转化成定基序列并进行季节调整后的数据表示，股票市场数据用境内上市公司的股票总市值（Stock）的月度数据衡量，其中Stock数据来自于万得数据库。为避免时间序列存在伪回归现象，首先采用ADF检验法检验各序列的平稳性。ADF检验结果表明：在5%的显著性水平下，原序列均存在单位根，一阶差分序列不存在单位根。因此，[Lt]、[St]、CPI、Stock均为一阶单整序列，即I（1）过程，满足对序列进行协整关系检验的条件。

（二）Johansen协整检验

1. 最优滞后阶数的选择。分别建立[Lt]、[St]、CPI和[Lt]、[St]、Stock的三变量VAR模型，依据LR、FPE、AIC、SC、HQ准则，本文选择[Lt]、[St]、CPI的滞后期为2，可知协整方程的最优滞后阶数为1；选择[Lt]、[St]、Stock的滞后期为2，协整方程的最优滞后阶数为1。

2. 协整关系的检验。迹检验和最大特征值检验的结果显示：在5%的显著性水平下，[Lt]、[St]、CPI之间存在1个协整关系；[Lt]、[St]、Stock之间存在1个协整关系，可以建立向量误差修正模型。

（三）向量误差修正模型（VEC）

1. 估计VEC模型。用结构因子[Lt]、[St]的估计值分别与通货膨胀水平CPI和股票市值Stock形成三维向量时间序列，建立向量误差修正模型，采用一阶差分的滞后阶数。估计结果如下：

其中D表示一阶差分，*表示对应的参数估计t统计量绝对值小于1，参数显著性很低，不足以作为分析的依据（沈根祥，2011）。

2.基于VEC模型的Granger因果关系检验。Granger因果关系检验结果表明：在5%的显著性水平下，CPI是[St]的Granger原因，CPI不是[Lt]的Granger原因；在10%的显著性水平下，Stock是[St]的Granger原因，Stock不是[Lt]的Granger原因。

通货膨胀率和股票市值对斜率因子影响效果明显，对长期因子影响不显著。通货膨胀水平和股票市值对债券市场的影响具有时效性，对斜率因子的影响较为显著，但是对长期利率的影响是通过改变市场预期而间接实现。一方面表明中国金融市场发展逐渐成熟；另一方面表明这些因素的波动在传导至利率长端的效果明显被削弱，金融市场中存在一定程度的无效性，不能从收益率反映出市场的全部信息。水平因子主要受其自身因素影响（何晓群和王彦飞，2014；陈浪南和郑衡亮，2015）：一是因为中国很长时期内对存款利率实行管制，国债利率与各期限存款利率高度相关，导致水平因子不能及时反映出宏观经济的变化；二是商业银行是银行间国债市场的主要买家，银行存款和资金量会影响期限结构。样本区间是从2007年开始，商业银行在满足资本充足率和风险监管要求外，大部分资金用于购买国债，银行资金较为宽松。

误差修正模型包含了通货膨胀率和股票市值对利率期限结构的短期动态影响和长期均衡影响。短期动态影响写成单方程形式为：

模型中[Vecm]为误差修正项，误差修正项系数反映了在VEC模型中序列之间动态关系偏离长期均衡时的调整力度。若其为负值，则意味着偏离的误差将会得到修正。模型（3）中对斜率因子的调整的系数为

-0.199，表明斜率因子的短期波动幅度较大，平均每月对上月偏离长期均衡水平的短期调整幅度为19.9%，当短期波动偏离长期均衡时，经济系统将以19.9%的调整幅度将其拉回到长期均衡状态。模型（4）中对斜率因子的调整系数为-0.219，表明斜率因子平均每月对上月偏离长期均衡水平的短期调整幅度为21.9%，当短期波动偏离长期均衡时，经济系统将以21.9%的调整幅度将其拉回到长期均衡状态。修正项对斜率因子的负向边际贡献也表明斜率因子偏离长期均衡的波动持续性较弱，在偏离长期均衡时，会进行反向调控使其恢复到均衡水平。

在经济变量对利率期限的长期均衡影响中，将[St]（-1）的系数标准化为1，得出变量间的长期均衡关系为：

（四）通货膨胀水平、股票市值对国债利率期限结构的影响

通货膨胀水平对债券市场斜率因子的影响效果显著，从侧面说明中国投资品种逐渐健全，当通货膨胀水平变化（或者实际利率变化）时，居民会调整投资组合。股票市值变动对斜率因子的影响效果也较为显著，表明中国金融市场的效率明显提升，市场参与者可以迅速觉察到金融市场的变化而重新分配资产。宏观经济和金融市场的变化对长期利率的影响效果并不显著，间接反映出货币政策通过债券市场传导的有效性尚不完整。

通货膨胀率和股票市值对利率期限结构的影响可以分为短期动态影响和长期均衡影响。短期内，通货膨胀水平的变动（DCPI）增加会缩小斜率因子的变化（[DSt]），当通货膨胀水平变动幅度较大时，市场对于变动方向形成强烈的预期，因而长短期利率的变动幅度趋于稳定，斜率因子的变化趋缓。股票市值的变动（DStock）增加会加剧斜率因子的变化（[DSt]），当股票市值波动幅度变动，短期内投资于股市的资金流动增加，会加大债券收益率的波动，导致斜率因子的变化幅度增加。

通货膨胀率和股票市值对利率期限结构的长期均衡影响与短期动态影响有所不同。从长期来看，通货膨胀率和股票市值均在缩小斜率因子方面效果显著。斜率因子变小有两方面原因：一是长期利率下降，意味着居民和企业对长期资金的需求疲软，固定资产投资对社会总需求的拉动作用较弱，导致经济活动活跃度下降；二是短期利率提升，意味着货币政策开始收紧，其后果是经济活动的下降。长期投资意愿减弱也表明市场对未来不确定性增加，长期投资意愿不强，风险偏好下降，短期投资意愿增加。因此，斜率因子缩小会对经济活动下降有预测作用。由于中国对于通货膨胀的调控效果明显，市场对货币当局的调控能力信心较强。当通货膨胀水平较高时，市场解读为央行为抑制经济过热，会采取紧缩的货币政策，短期利率会随之提高，由于价格刚性的存在，长期利率上升幅度低于短期利率，利差收窄，斜率因子变小，通货膨胀对斜率因子的负向影响较为显著（金雯雯和陈亮等，2014；何晓群和王彦飞，2014）。当股票市值增加时，股市繁荣，市场投资于股市的积极性增加，部分投资者将资金从债券市场转移到股票市场，导致债券市场的利差缩小，收益率曲线趋于平坦。

当前经济下行压力依然较大，新常态的特征明显，受去产能、去泡沫和清理债务等因素影响，基础建设投资、民间投资等出现下滑。除了宏观经济因素和金融市场因素对利率期限结构产生重要影响外，债券市场自身因素也会使利率期限结构发生改变。债券市场频频出现违约，刚性兑付逐渐被打破，债券市场的波动也改变了利率期限结构。

五、利率期限结构对通货膨胀的预测分析

利率期限结构反映的是预期未来宏观经济信息，因此利率期限结构的水平因子和斜率因子包含着通货膨胀水平和通货膨胀预期的信息。例如，当通货膨胀率相对高时，人们预期未来通货膨胀率会降低，于是长期债券的收益率将会降低，长短期利差缩小。Rudebusch和Wu（2008）认为水平因子反映了通货膨胀预期；吴吉林（2010）利用NS宏观金融模型分析利率期限结构因子与宏观经济变量之间的关系，发现水平因子包含预期通货膨胀信息；李宏瑾等（2010）利用Mishkin模型考察利率期限结构对通货膨胀的预测能力，发现中短端利率曲线对通货膨胀的预测能力较强；康书隆和王志强（2010）采用Diebold-Li方法估计中国国债的利率期限结构，对CPI和长期利率两个序列做时差相关分析，发现长期利率可以预测CPI的走势。国内外研究发现，长短期利差对预测未来6个月到1年后的通货膨胀率效果较好。表3描述了2007—2015年利率期限结构的水平因子、斜率因子、同期通货膨胀率、6个月后的通货膨胀率4个变量的相关系数。

通过相关性分析，利率期限结构的斜率因子与未来6个月的通货膨胀率呈现出较强的负相关。郭涛和宋德勇（2008）选取2004—2006年数据，发现中国长短期利差和未来6个月的通货膨胀率呈负相关，长短期利差与斜率因子高度相关（相关系数达0.976），也证明了中国斜率因子与未来通货膨胀率的负相关关系。短期利率受央行基準利率调整和短期资金供求关系的影响较大，而通货膨胀率则是央行制定货币政策的重要参考指标。通货膨胀率与短期利率呈现正相关关系，斜率因子则和通货膨胀率负相关。下面对斜率因子和未来通货膨胀率进行回归分析，建立简单回归方程为：

利率期限结构的斜率因子在统计上对通货膨胀率具有显著的预测能力，可用于对通货膨胀水平未来变动方向的定性和定量分析。利率期限结构的斜率因子对通货膨胀水平产生负向影响，当[St]增加时，未来的通货膨胀及通货膨胀预期将下降。从Nelson-Siegel模型斜率因子走势分析，2016年下半年CPI同比将保持在1%—2.5%的区间内温和趋势运行，不存在明显的通胀或通缩压力。同时斜率因子逐渐缩小，预计通货膨胀水平有上升的趋势，这与2016年下半年以来的实际情况相符。斜率因子缩小预示着经济活动活跃度下降，政策的稳定性对提振投资信心至关重要，央行应保持宏观经济政策稳定，关注通货膨胀变化和股票市场变化对国债利率期限结构的影响，并从利率期限结构所隐含的市场预期因素进行决策，可根据货币政策的时滞，注重松紧适度，灵活运用多种货币政策工具，提前采取较为稳健的货币政策。

六、结论

本文利用Nelson-Siegel模型拟合了中国利率期限结构曲线，并构建VEC模型等分析通货膨胀水平、股票市值与国债利率期限结构的关系和斜率因子对未来通货膨胀率的预测效果。研究表明，通过动态Nelson-Siegel模型估计的水平因子、斜率因子和曲率因子体现出利率期限结构的特征，能够有效刻画对于宏观经济等变量变化的预期及其自身的内生周期性特征；通货膨胀率、股票市值与国债利率期限结构的水平、斜率因子之间存在长期的协整关系，但是通货膨胀率和股票市值均不能显著引起水平因子的变化，水平因子与存款利率相关性较高，反映出货币政策向债券市场传导的效率有待完善；通货膨胀水平和股票市值均能显著引起斜率因子的变动，短期看来通货膨胀水平和股票市值影响斜率因子变动的方向不一致，但长期看来通货膨胀水平和股票市值均在缩小斜率因子方面效果显著，进一步证明了Fisher方程中斜率因子包含着通货膨胀水平预期变动的结论；斜率因子还可以作为预测未来通货膨胀的重要指标。

在中国债券市场逐步开放和货币政策调控逐步从数量型转向价格型的背景下，中国国债利率期限结构已经显示了对经济的预测功能，货币政策通过债券市场传导的基本条件已具备。但是与西方发达国家相比，中国政府部门对此预测功能的分析和应用有待进一步开发，同时中国货币政策向债券收益率的传导效率较低，收益率曲线的有效性仍需提高。主要原因是中国债券发行期限结构、流动性、二级市场等尚不完善，各种因素从多种渠道弱化或扭曲了利率传导效率，也容易产生套利机会。因此，为进一步完善货币政策通过债券市场的传导效果，应当完善国债发行结构，并发展国债衍生品市场，提高二级市场流动性，通过大规模的市场交易，提高无风险利率的基准性，畅通价格型政策的传导渠道。

参考文献：

[1]Blundell A.， Browne F.， Manasse P.1990. Monetary Policy in the Wake of Financial Liberalization， OECD Working Paper， No. 77.

[2]Dewachter，H.and Lyrio，M. 2003. Macro Factors and the Term Structure of Interest Rates，Working Paper of ERIM Report Series reference，No.ERS-2003-037-F&A.

[3]Dewachter M.， Lyrio M. 2006. Macro Factors and the Term Structure of Interest Rates[J].Journal of Money， Credit and Banking， 38（1）.

[4]Diebold F.， D. Rudebusch，B.Aruoba. 2006. The Macroeconomy and Yield Curve： a Dynamic Latent Factor Approach[J].Journal of Econometrics，127.

[5]Diebold，F.X.，and Canlin Li. 2006. Forecasting the Term Structure of Government Bond Yields[J].Journal of Econometrics，130（2）.

[6]Estrella A.， Mishkin F. 1997. The Predictive Power of the Term Structure of Interest Rates In Europe and in the United States：Implications for the European Central Bank， European Economic Review，41（7）.

[7]Francis X.Diebold， Canlin Li. 2006. Forecasting the Term Structure of Government Bond Yields[J].Journal of Econometrics.

[8]John Y. Campbell，Adi Sunderam，Luis M. Viceira. 2013. Inflation Bets or Deflation Hedges？ The Changing Risks of Nominal Bonds.NBER Working Paper.

[9]Ilmanen， A. 2003. Stock-Bond Correlations[J].The Journal of Fixed Income，12（2）.

[10] 陳晖，谢赤.国债收益率曲线在货币政策制定与实施中的作用[J].求索，2006，（6）.

[11] 郭涛，宋德勇.中国利率期限结构的货币政策含义[J].经济研究，2008，（3）.

[12] 韩学红，郑妍妍，伍超明.对我国股票收益率与通货膨胀率关系的解释：1992—2007[J].金融研究，2008，（4）.

[13]胡志强，王婷.基于Nelson-Siegel模型的国债利率期限结构预测[J].经济评论，2009，（6）.

[14]李宏瑾，钟正生，李晓嘉.利率期限结构、通货膨胀预测与实际利率[J].世界经济，2010，（10）.

[15]刘金全，王勇，张鹤.利率期限结构与宏观经济因素的动态相依性——基于VAR模型的经验研究[J].财经研究，2007，（5）.

[16]沈根祥.货币政策对利率期限结构的影响——基于动态Nelson-Siegel模型的实证分析[J].当代财经，2011，（3）.

[17]沈根祥.基于动态Nelson-Siegel模型的利率期限结构预期理论检验[J].上海经济研究，2010，（4）.

[18]汪冬华，雷曼，阮永平，汪辰.中国股市和债市溢出效应在牛熊市中的异化现象——基于上证综合指数和中债总指数的实证研究[J].预测，2012，（4）.

[19]汪军红.宏观经济变量对我国国债收益率曲线的影响分析[A].中国数量经济学会2006年会论文集，2006，（10）.

[20]王一鸣，李剑峰.我国债券市场收益率曲线影响因素的实证分析[J].金融研究，2005，（1）.

[21]王茵田，文志瑛.股票市场和债券市场的流动性溢出效应研究[J].金融研究，2010，（3）.

[22]余文龙，王安兴.基于动态Nelson-Siegel模型的国债管理策略分析[J].经济学（季刊），2010，（4）.

Abstract：This article chooses the dynamic Nelson-Siegel model to build level，slope and curvature factors which can reflect the term structure of interest rate of national bonds，using national bonds yield data from January 2007 to June 2016. The method of Johansen cointegration test，VEC model are used to measure the behavior characteristics between inflation，stock market value and the term structure of interest rates. We find that the structure factors reflect the characteristics of the term structure of interest rates through the Nelson-Siegel model. There exists the long-term cointegration relationship between inflation，stock market value and the level and slope factors .However，the change on inflation and stock market value have little effect on the level factor，which reflects that the transmission efficiency of monetary policy to the bond market needs to be improved. In the long run，the change on inflation and stock market value can narrow the slope factor significantly. In addition，the slope factor can predict the change of inflation and provides forward-looking information for the formulation and implementation of monetary policy.

Keywords：term structure of interest rate，inflation，stock market value，dynamic Nelson-Siegel model