基于SPBI模式的维吾尔族地区中小学数学教学探索

韩花荣

(喀什大学教育科学学院，新疆喀什 844008)

基于SPBI模式的维吾尔族地区中小学数学教学探索

韩花荣

(喀什大学教育科学学院，新疆喀什 844008)

SPBI教学模式是以数学活动情境为基础，数学问题为纽带的启发式教学。在维吾尔族中小学课堂中，借助SPBI教学模式，构建维吾尔文化背景的数学活动情境，能引起学生情感的共鸣，利于对数学知识点的理解。介绍维吾尔族的数学文化，为创设教学情境做铺垫；建构维吾尔族中小学数学SPBI教学模式的理论基础；探索维吾尔族中小学数学SPBI教学模式的教学实践。

SPBI教学模式；少数民族数学教学；民族数学文化；情境认知；教学案例

PDF获取： http://sxxqsfxy.ijournal.cn/ch/index.aspx doi： 10.11995/j.issn.2095-770X.2017.02.021

2000年，汪秉彝和吕传汉在《创新与中小学数学教育》中提出了培养中小学生创新意识的数学教与学的基本模式,并于2001年9月起，在贵州、云南、四川开展了数学“情境-问题”教学实验研究。SPBI教学模式的应用迁移到物理、政治、地理等学科的课堂教学，正在发展成为一种更大范围的“设置情境与提出问题”的基本学科教学模式。通过实验研究，SPBI教学模式在2000年的基础上已经有很大的发展。维吾尔族地区的中小学数学教材以主流文化为背景，脱离了学生的日常生活，学生学习易产生认知障碍。为提升维吾尔族数学基础教育，数学课堂教学应该从学生熟悉的民族文化出发，创设民族数学文化的情境，引导学生主动探究，提出问题、分析问题和解决问题，进而达到课堂教学的目的。

一、维吾尔族的数学文化

维吾尔族是中国的一个古老的民族，在其发展的历史上形成和发展了丰富的传统文化，数学文化是其中的一种。但它散落在人们的饮食、 衣着、生产、建筑中，也存在于语言文字、文学艺术、宗教、风俗等方面。对其信息进行收集和整理，并深度挖掘，有利于促进维吾尔族地区数学基础教育的发展。

(一)维吾尔族传统服饰

不同民族的服装在图案、色彩、形制方面各具特色，可以说不同民族相互区别的标志之一就是服装。维吾尔族姑娘的衣服多以饱和鲜艳的色彩为主；妇女则喜欢闪闪发光的织物，尤其是头巾。冬天头巾的形状多为正方形和三角形，闪着金光和银光；夏天多为长方形。维吾尔族妇女自古就有穿裙子的风尚，它是妇女主要的服饰。维吾尔族信仰伊斯兰教。斯兰教禁止描绘人或动物在服饰上，因此，维吾尔族人民就将植物与现实生活中的事物结合起来了。例如，将生活中的琴、坛、瓶及各种类的花、果实、枝藤，用弧线、直线、曲线构成新月形、菱形、三角形、长方形等不同图形，占据着一定的比例，装饰着维族服饰(见图1)[1]。

图1 维吾尔族传统服饰

(二)维吾尔族的建筑

维吾尔族的数学文化存在于民族服饰，也渗透在典型建筑中。首先是国家5A级景点——喀什老城的高台民区。该地房屋随着地势营建，相互交错、套叠。但门户禁止朝西开放，室内壁翕较多，并在壁翕、走廊、墙面上多有装饰。维吾尔族民居院门都是实木，房间的门窗也是木制，但窗户有其特色，突出是双层结构窗户，内层是木框玻璃窗，外层实体木框。外层木框可以旋转180°，也就是说外窗可以完全打开与关闭。另一种窗户是气楼天窗，形状正方、八角等，并只设窗框而没有玻璃。房子前面的柱子有木、砖两类，木柱在人高的部位有雕花，它的形状有八角、方、棱、圆等(见图2)[2]。

维吾尔族建筑清真寺装饰几何纹样很有特色。通常以菱形、方形或圆形为基础图形，或加入圆弧、对称、交错、循环等手法等，再经过不同的交叉、组合，最后形成二方或四方连续的构图(图2)[3]。

图2 维吾尔族建筑物

(三)新疆地毯

新疆地毯种类众多，图案多变，虚实相当，色泽鲜艳，对比谐调，它即是一种历史记忆，更是一种艺术形式。新疆地毯的功能有铺挂御寒和陈列装饰两种。其基础纹样多是三角形、圆形、菱形、方形、多边形等，且菱形占主导地位。各类图案纵横呈90度、斜度呈45度走向，并严格限制在井、田、米字格内。也就是说，新疆地毯的图案结构已经规则化和定型化(图3)。有史料表明，新疆地毯既是新疆与疆内交换的主要物品，也是历来丝绸之路上中外交流的重要物质。

图3 新疆地毯

二、维吾尔族中小学实施SPBI教学模式的理论基础

(一)SPBI概述

SPBI(Situated Problem Based Instruction)教学模式是“基于情境的问题教学”的简称，是2001年在吕传汉和汪秉彝教授的倡导下，西南地区部分学校开展的一项基础教育课堂教学实验。[4]该教学实验的出发点主要是解决中小学生提出数学问题能力低下的现状，落实课堂教学培养创新型人才的目标，促进基础教育新课程改革的开展。经过若干年的改进与发展，该模式已经取得了丰硕的成果。

中小学“情境——问题”数学学习适用对象是中小学生。“情境——问题”教学模式需要考虑，数学情境应是学生日常生活中熟悉的情境，根据学生的实际和知识形成的背景创设；重视课堂中学生问题意识的培养。创设两难情境，启发学生提出问题，激发学生的认知冲突，以问题为纽带使学生主动分析问题和解决问题，获得适应社会和进一步发展的数学知识、数学思想方法和数学应用技能。教学活动中，学生始终敢于并善于质疑，做到独立探索和合作探索；教师始终处于启发指导地位，并且教师树立多给学生动口、动脑机会的理念。其基本模式见图4。

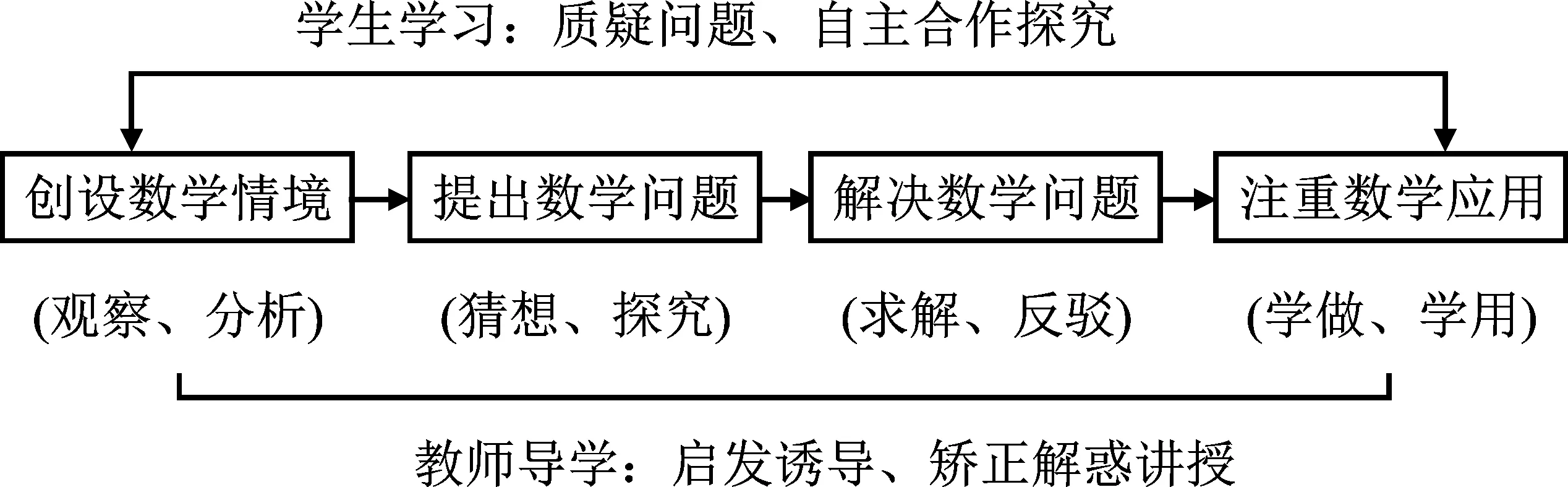
图4 情境——问题教学模式

从上述基本模式中可看出，创设数学情境是前提，提出数学问题是核心。本文着眼于促进维吾尔族中小学生对数学知识的理解，数学情境创设结合维族日常生活中的民族数学文化知识，使学生对所学知识感兴趣，引起情感上的共鸣，促进学生观察分析数学情境，并进行猜想探究，提出数学问题。在数学问题的提出向数学问题解决过程中，教师进行教学启发，激发学生的认知冲突，让学生学会自己反驳、求解，并辅以适当的解惑讲授，帮助学生解决问题。知识的学习在于运用，任何知识都要以应用为目的。学生要做到活学活用，教师教学要以能让学生运用数学知识为主要目标之一。另外，情境问题教学模式是不断延伸、无限循环的过程，形式为“情境—提问—解决—应用—情境—提问—解决—应用……”。

(二)维吾尔族中小学实施SPBI教学模式的心理学基础

SPBI的心理学基础之一是情境认知理论。早期的研究来自于杜威、列昂杰夫和维果斯基等著名学者。例如，维果斯基认为认知是在社会情境中开展的智慧活动，并经过内化才能得到发展。情境认知理论是一个复杂的系统，有丰富的内涵，以下主要从知识观、学习观、教学观、评价观探讨。

1.情境认知理论的知识观

知识是在个体与社会互动中产生的，而非个体内部的心理表征。知识来源于真实的活动或情境，也就决定了人们只有在情境中才能真正的理解它。同时，也决定了知识必须运用真实的情境，才能发挥其应有的作用和功能。知识的表征方式多种多样，体现在行为、图像和符号的方式；既存在于书籍、报纸、期刊、杂志等物质载体中，也存在于网络、视频、音频等虚拟媒介中[5]。学生的数学学习既要“入境”又要“脱境”。“入境”为了知识的内化、外化和条件化，可以帮助学生更好地理解，获得数学学习的意义；“脱境”为了知识的转化和生成，达到灵活应用。因此，数学学习要处理好情境和非情境化之间的平衡。每个民族都有自己的民族文化，民族数学文化是民族文化中的一部分，它散落在人们生活的各个角落。如维吾尔族的数学文化存在于其特色饮食、服饰、文字、宗教、地毯、民间故事等情境中。只有通过分析、抽象才能用文字语言、数学术语概括表达出来，最终成为民族数学文化知识。民族数学文化知识来源于日常生活情境，只有将它们引入课堂教学加工成数学教学情境，维吾尔族中小学生才容易理解数学知识，并可使学生直接用于解决实际问题。

2.情境认知理论的学习观

情境认知理论高度关注自然状态下的真实情境，认为它是学习者知识获得和学习发生的必要条件，学习者只有通过真实情境的学习才有助于理解和内化，提高学习者解决现实生活中问题的能力。该理论既要求将知识的学习置于真实的情境中，也要求学习者积极参与真实的文化实践探索。民族地区和发达地区学生数学学习是有差异的。新疆师范大学的方新荣指出，这种数学差异不是先天的遗传因素决定的，而是民族文化背景(宗教、地域、语言、生活习俗等)的不同造成的。维吾尔族儿童早期的数学感知来自于本民族的社会环境、家庭教育和生活熏陶，自然带来浓郁的民族文化色彩。若数学教育仅以主流文化为背景设计数学课堂教学，维吾尔族儿童就会感到陌生，会产生认知障碍。人成才必须要有创新意识和创新能力，创新来源于问题，没有问题就没有创新，问题只有在真实的情境中才能发现。因此，对维吾尔族学生的数学教育必须以维吾尔族文化背景设置课堂教学情境，并在学生的观察和老师的启发诱导下，激发学生质疑、探究、提出数学问题。这种方式既加深学生对数学知识的理解，又培养维吾尔族学生的问题意识，增强创新能力。

3.情境认知理论的教学观

教师教学时，应把知识镶嵌在情境当中，为学生创设扮演多种角色情境的机会，实现学生有意义的学习。教师始终发挥启发诱导的作用，特别是在学习的关键时刻教师应搭建脚手架，促进学生跨越最近发展区，达到获得知识的目的。在教学过程中教师要注重学习共同体的创设，要扩大教学中的默会知识。同时为使教学达到良好的效果，教师也要对学生的学习过程和教学过程进行反思，吸取经验教训[6]。

情境-问题教学模式要求教师应以维吾尔族日常生活中的数学文化为背景创设课堂教学情境，启发诱导学生质疑、提问，使学生将来自于本民族数学文化中的数学感知与课堂数学材料结合。进而维吾尔学生数学思维就能得以顺利的延续、过渡，产生有意义的学习。在这一过程中，教师要充分发挥其搭建脚手架的作用。教师也要进行教学反思，将课堂中的出现问题、学生的状况等进行记录总结，为以后的数学教学提供有益的借鉴。

4.情境认知理论的评价观

评价观强调评价学习者的参与性，评价的背景必须是真实的镶嵌知识的学习情境或模拟的真实性任务，不能是虚拟想象的学习情境。评价的标准不唯一，考虑问题的多个方面，从多个角度评价。因此，评价的结果是多样的。评价的核心是学生的认知过程，即学生在真实的学习情境中，在教师的启发引导下，在学生的质疑探究过程中提出问题、分析问题、解决问题，最后达到应用知识的目的。评价既关注获得知识的结果，也关注学生知识结构和认知策略的发展。基于情境-问题教学模式的教学评价始终围绕数学课堂教学情境，强调学生上课时的积极性和兴趣，在教师的启发指导下，学生上课观察、发现问题的能力，提出数学问题的数量和质量，学习小组的交流和互动。总之，该教学模式既注重学生数学学习认知过程，更关注学生课堂的参与性，学生从数学情境中所学知识的应用性。

基于以上分析，提高新疆地区维吾尔族中小学生的数学水平，必须采纳并大力推广基于民族数学文化的情境-问题教学模式。一方面，可以激发学生兴趣，引起情感的共鸣，利于学生对数学知识点的理解；另一方面，使教师能够把握学生的最近发展区，设置情境问题最终使学生跨越最近发展区，获得知识。同时改变死读书的现状，让维吾尔族中小学生在熟悉的教学情境中轻松学习数学知识，提高学生的创新能力。

三、SPBI教学模式的实践

本节课是小学五年级上学期关于轴对称图形的教学课。由喀什市某小学数学老师执教。教学情境如下。

(一)用多媒体(PPT)播放一些美丽蝴蝶图形(见图5)

图5 蝴蝶图形

教师：同学们，看PPT上的蝴蝶图案，它们好看么？

学生：好看。

教师：那同学们看着这些美丽蝴蝶，你有什么想说的么？

学生(1)：蝴蝶很漂亮，形状和颜色很好看。

学生(2)：蝴蝶左右两边一样。

教师：想一想，我们身边还有哪些事物具有这样的特点?

学生举例，老师倾听。

教师：同学们，我们给具有这种特性的图形一个名字？

学生讨论，老师给予指导。

学生翻书，明确这样的图形在数学中叫轴对称图形。

(二)动手操作，合作学习

发给每个小组一张方格纸，上面有矩形、正方形、三角形、菱形、平行四边形。要求学生动手折一折、剪一剪，看看那些图形是轴对称图形，画出对称轴，并按一定的方式进行分类。乙组的分类是把平行四边形分在了有一条对称轴的一类，但遭到余下组的质疑。

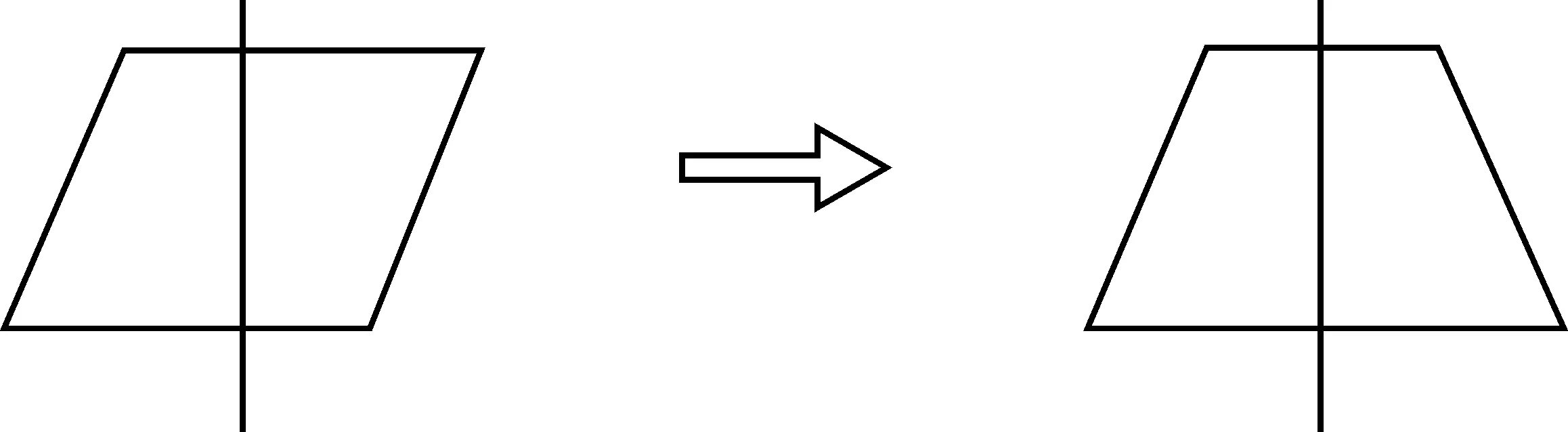
图6 乙组操作展示图

乙组：利用投影仪，给平行四边形画一条对称轴，如图6所示。然后用剪刀沿线剪开，拼成如图6中的等腰梯形，因此我们认为平行四边形也是轴对称图形。

学生A马上提出了反驳：轴对称图形是指某一图形沿着一条直线对折后直线两旁的部分完全重合，并且只能就原图而言。

乙组(有些迟疑)：我们沿直线用剪刀剪开，直线两部分是完全重合的。

学生A：书上讲轴对称是就原图形来说的，在这里是不能重组图形的。

乙组同学回答不上来，班级其他同学开始小声议论，各有支持者。并且乙组的部分成员开始赞成学生A的观点。

老师：你们认为谁说得有道理?

学生：学生A，因为轴对称图形应在不改变原图形形状的基础上来判定的。

此时，乙组学生也点头同意了。

老师：其实，平行四边形也是对称图形，只不过它不是我们今天学的轴对称图形，而是中心对称，这个我们以后会学到。

(三)把所学知识运用到生活中

老师：轴对称图形在生活中有许多地方都会用到它，例如我们的服饰、地毯、建筑等。下面我们一起来欣赏一组作品。(PPT展示见图7)

图7 PPT展示图形

学生A：第五幅不是轴对称图形，因为如果对折，另一边没有与它相对应。

老师：如果我们想把它变成轴对称图形，可以怎样做?

学生B：最下面的一朵紫花去掉，然后接下来的最后两朵花弄相同就可以了。

老师：还可以怎样?

学生C：去掉最下面两朵红花，添一朵紫花与左边的对称也可以。

学生D：还有第六幅也不是轴对称图形。因为里面的图形不对称，而且对应位置也不同。

老师：同学们观察得仔细，那你们看前四幅是轴对称图形吗?

学生：是。

老师：第四幅的对称轴在那?

学生用手示意给老师看，是顺着图案中间垂直的也可以是斜方向的。

老师：对，这说明对称轴不只是有垂直方向的，还可以有其它方向。(老师用手掌变换不同方向以示意)

老师：今天咱们学习了轴对称图形，很漂亮对吧。同学们想不想利用今天所学的知识动手剪一些美丽的剪纸。

学生在下面剪纸，老师将学生的作品贴在黑板上。

学生A：第四幅作品不美观。

学生B：第四幅作品不是轴对称图形，因为它左右不对称。

老师假意要把该作品拿下来，几乎同时

学生D：老师你贴错了，我是这样折起来剪得。(学生用手示意老师，他是斜着对折后剪得)

为什么又把它贴回黑板呢？因为我们刚才知道轴对称图形的对称轴可以是垂直的，也可以是其他方向，那这幅图的对称轴是什么方向呢？

学生：斜方向。

四、结语

总之，民族地区大力提倡情境——问题教学模式，是将素质教育、创新教育目标落实在不同民族文化背景的数学学科课堂教学的有益探索。构建融入民族数学文化的教学情境，运用于中小学数学课堂，是促使民族地区数学教学质量提高的根本途径。但在维吾尔族地区大力推广这一模式，还属于初步的探索阶段，有若干方面问题亟待解决。比如维吾尔族数学文化的深入挖掘；良好的维吾尔族数学文化情境的创设及判断标准；基于SPBI的维吾尔族校本教材的探究以及对民族地区教师民族数学文化方面的培训等方面。这些工作需要社会各界协同合作，任重而道远。

[1] 李凯.维族服装形制在服装结构中的应用[J]. 黑龙江纺织，2014(2)：19-21.

[2] 母俊景. 新疆维吾尔族传统民居建筑技术与艺术特征研究[D]. 乌鲁木齐：新疆农业大学，2009.

[3] 刘超，张茜，阿依古再丽.维吾尔族数学文化调查分析[J].兵团教育学报，2012，22(6):9-28.

[4] 吕传汉，汪秉彝. 中小学“数学情境与提出问题”教学的理论基础及实施策略[J]. 贵州师范大学学报，2007，25(1)：95-100.

[5] 闫桂琴，崔克忍.中学数学教学论[M].北京：北京师范大学出版集团，2010：20-22.

[6] 刘亚龙.基于情境认知理论的大学英语多媒体网络教学研究[J].电化教育研究，2009(7)： 113-120.

[责任编辑 李亚卓]

Study on the SPBI Model of Mathematics Teaching in Primary and Secondary School of Minority Nationalities

HANHua-rong

(CollegeofEducationScience,KashgarUniversity,Kashgar844008,China)

SPBI teaching model is the heuristic teaching which is based on mathematics activities situation and is linked of mathematics problems .In the Uygur primary and secondary schools with the help of SPBI teaching model, the mathematical activity situation of the Uyghur cultural background can be constructed, which can arouse students' emotional resonance and help to understand the mathematical knowledge. The purpose of this paper introduces the mathematical Uighur culture, lays the groundwork for the creation of the teaching situation, constructs the mathematical theoretical basis of SPBI teaching pattern of Uighur primary and secondary school, and explores the teaching practice of SPBI teaching mode of Uighur primary and secondary school.

SPBI teaching mode; mathematics teaching of minority nationality; national mathematics culture; situated cognition theory; teaching cases

2016-10-02

2013年教育部人文社会科学研究基金新疆项目(13XJJC880003)

韩花荣，女，河南周口人 ，喀什大学教育科学学院2015级学科教学数学专业硕士研究生。

■学科教育

G623

A

2095-770X(2017)02-0096-05