行波超声波电动机单输入Takagi-Sugeno模糊转速控制

张 萌，史敬灼

(河南科技大学，洛阳 471023)

行波超声波电动机单输入Takagi-Sugeno模糊转速控制

张 萌，史敬灼

(河南科技大学，洛阳 471023)

超声波电动机的运行过程具有明显的非线性。适当的电机控制策略，是促进超声波电动机更广泛应用的重要前提。给出一种适用于超声波电动机转速控制的单输入Takagi-Sugeno模糊控制器。与传统的模糊控制器相比，该控制器结构简单，减少了设计工作量与在线计算量。实验表明，Takagi-Sugeno模糊控制器控制效果较好。

超声波电动机；转速控制；模糊控制；Takagi-Sugeno

0 引 言

超声波电动机(USM)因其不同于传统电磁电机的独特优点，已在众多领域应用，并有着广泛的前景[1]。超声波电动机有多种类型，行波超声波电动机是其中研究、应用最多的一类。行波超声波电动机的运行过程具有明显的非线性和时变特征[1-2]。近年来，为了有效应对电机的非线性，具有本质非线性的模糊控制策略受到重视[3-5]。

将模糊控制用于超声波电动机的具体方法，主要可分为两类。一类是用模糊逻辑设计调节器，在线调节转速或位置控制器的参数。较为常见的是模糊PID控制器[3-4]，转速/位置控制器为PID控制器，设计模糊调节器在线调节PID控制器的参数。例如，文献[3]给出了3个分别包含49条规则的模糊规则表，可用来对PID控制参数进行在线调节。文献[4]同样给出了这样的模糊规则表，并引入免疫调节机制以改善性能。另一类是将模糊控制器直接用做电机转速或位置控制器，具体形式多是以转速/位置误差、误差变化率两个变量为输入的二输入模糊控制器，也可以是文献[5]采用的模糊神经网络结构。为使模糊控制器的动态控制特性与超声波电动机自身的运行特征相适应，通常需要对模糊控制器做离线优化设计与在线动态调整。离线优化设计往往基于动态测试数据，设计工作量大。在线的动态调整，虽然通常采用调整量化因子或比例因子的方法以降低复杂度，但仍然会增大在线计算量。

本文通过对超声波电动机PID转速控制性能的研究，给出一种用于超声波电动机转速控制的单输入Takagi- Sugeno(T-S)模糊控制器。该控制器的设计以PID控制参数为基础，减少了设计工作量；采用单一输入变量，减小了在线计算量和复杂度。实验表明，控制效果较好。

1 超声波电动机PID转速控制性能

PID控制器的时域表达式：

(1)

式中：u为控制量，e为误差。KP，KI，KD为控制参数。以Shinsei USR60型两相行波超声波电动机为对象进行PID控制性能实验研究，控制系统结构如图1所示。图示系统包含电机两相驱动电压幅值的闭环控制，以使两相驱动电压幅值相等并可控。图中，E为光电编码器，用于检测电机转速；Uref，Nref分别为电机驱动电压幅值、转速的给定值。

对图1所示系统进行转速阶跃响应实验。实验结果表明，由于超声波电动机固有的运行非线性，不同转速情况下的电机控制特性存在明显差异。表1给出了不同转速情况下，分别进行PID控制器参数整定得到的不同参数值。实际应用中，电机系统可能运行在转速可调范围内的任意转速情况下。为得到任意转速情况下的PID控制参数，需要对表1所示数据进行拟合。采用多项式拟合等简单的拟合方法，与超声波电动机本体非线性之间的匹配程度往往不高，也就不易根据有限的实验整定数据计算出其它转速情况下的合适的PID参数值。针对这一问题，考虑到传统模糊控制器的特点，本文给出一种类似于PI控制器的单输入T-S模糊控制器。

2 单输入T-S模糊转速控制器

2.1 模糊控制器的结构

本文所提单输入T-S模糊控制器的结构，如图2所示。图2中，输入变量ω为当前电机转速的测量值，经模糊化、模糊推理、解模糊等步骤，得到单输入模糊推理系统的输出df。df为模糊控制器输出控制量的增量，再经积分环节，得到输出控制量f。图中解模糊环节用到另外两个变量e和ec，分别是当前电机转速的误差和误差变化率(即误差的微分)；这两个变量不参与模糊化、模糊推理等过程，仅用于计算输出控制量，因而不算作模糊推理系统的输入变量。

为便于对比，图3给出了目前常用的传统模糊控制器结构。从图上看，图2与图3控制器结构只是输入变量不同，下文将进一步说明两者的差异。

图3 传统模糊控制器结构框图

2.2 模糊控制器的设计

图2所示单输入模糊控制器输入变量ω的单位为r/min，其模糊语言值取为L，M，H3个。每个语言值对应的隶属函数选为非线性的高斯函数，以增强该模糊控制器的非线性拟合能力，来应对超声波电动机的非线性运行特性。高斯函数的表达式：

(2)

式中：c，σ为待定参数，分别用来确定高斯函数曲线的中心位置和宽度(即覆盖范围)。显然，当ω=c时，高斯函数值为最大值1；当ω取值偏离c时，函数值逐渐减小。对于ω的3个语言值L，M，H，我们希望ω分别为30r/min，90r/min，120r/min时，其隶属度，即隶属函数的值为1。所以，将L，M，H各自隶属函数的参数c值依次设定为30，90，120。

与输入变量的3个语言值对应，模糊规则设计为下列3条：

规则1：ifW=L，thendf1=A11·e+A21·ec

规则2：ifW=M，thendf2=A12·e+A22·ec

规则3：ifW=H，thendf3=A13·e+A23·ec

规则中，W为输入变量ω经模糊化处理之后得到的模糊变量；A11，A21，A12，A22，A13，A23为系数，常数。由表1，取A11=15，A21=0.8，A12=6，A22=3，A13=3.5，A23=3。

模糊控制器的在线计算中，分别计算当前ω值对应于3个语言值L，M，H的隶属度数值，也就得到了每条规则前提部分的满意度(DOF)，然后进行解模糊计算。与上述T-S形式的模糊规则相对应，图2所示模糊控制器的解模糊方法采用T-S解模糊方法，得模糊控制器输出控制量的增量：

(3)

式中：DOF1，DOF2，DOF3分别为上述3条规则前提部分的满意度值。

将上述3条规则结论部分的表达式带入式(3)，同时考虑图2所示模糊控制器中的积分环节，可得输出控制量f的表达式:

(4)

若令：

(5)

则式(4)可写为：

(6)

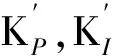
隶属度是式(2)所示隶属函数的计算结果。前述设计中，式(2)待定参数σ仍未确定。σ用来确定高斯函数曲线的宽度，也就决定了3个语言值L，M，H各自隶属函数之间的重叠范围。显然，σ值与式(5)一起决定了不同转速情况下的等效PI控制参数与表1所示整定值之间的拟合关系。为使这一拟合关系与超声波电动机的非线性特性相匹配以提高控制性能，以阶跃响应控制性能为评价指标，采用蚁群优化算法寻优得到3个语言值L，M，H各自隶属函数的待定参数σ值。具体寻优计算过程，请参阅文献[6]，此处不再累述。

至此，完成了图2所示单输入T-S模糊控制器的设计。

2.3 与传统模糊控制器的计算量对比

下面对比上述单输入模糊控制器与图3所示传统模糊控制器的在线计算量。模糊控制器的在线计算，主要是模糊规则前提部分，亦即各个输入变量隶属函数的计算；其计算量取决于规则的数量和前提部分的复杂度。

传统模糊控制器有e和ec2个输入变量，每个输入变量的语言值通常取为5或7个；其T-S形式的模糊规则：

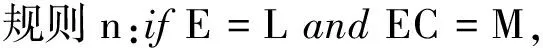
规则中，E，EC为e，ec对应的模糊变量，L，M代表输入变量的语言值，A0n，A1n，A2n为第n条规则结论部分的系数。

若每个输入变量的语言值都取为5个，则传统模糊控制器有25条规则。每条规则前提部分需计算2次隶属函数值，则一次模糊控制器计算过程中，需计算2×25=50次隶属函数值。而对于前述单输入模糊控制器，一次模糊控制器计算过程中，仅需计算1×3=3次隶属函数值。由此可见本文所提模糊控制器显著减少了在线计算量。

3 单输入T-S模糊转速控制实验

采用单输入T-S模糊控制器作为超声波电动机转速控制器，替换图1中的PID控制器，构成超声波电动机模糊转速控制系统进行实验研究。实验用电机仍为ShinseiUSR60型电机，电机驱动电路为H桥结构。在电机转速可调范围内，取不同的电机转速给定值，实测阶跃响应曲线如图4所示，可见不同转速情况下的控制性能接近，且控制效果较好，响应速度快，无超调。

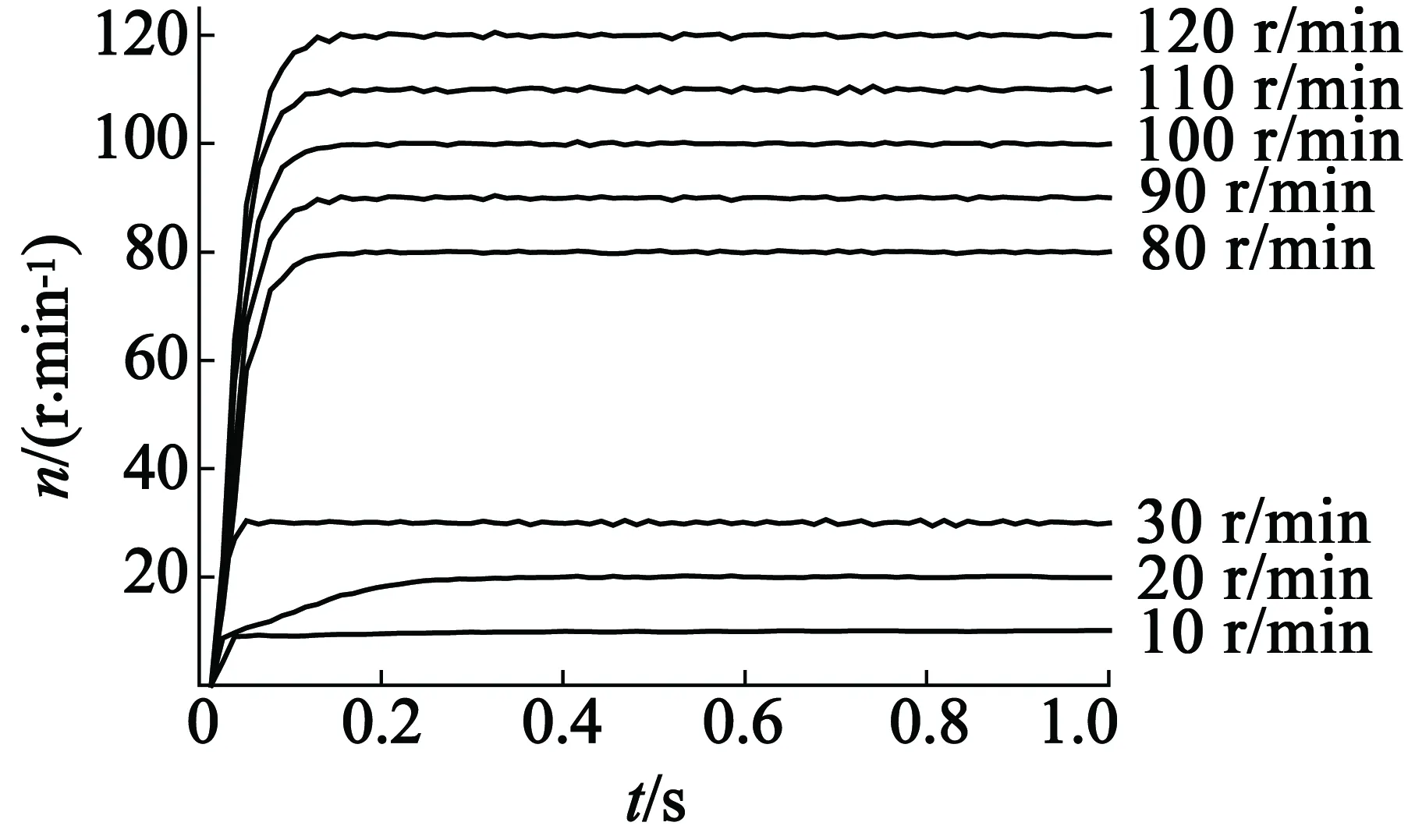
图4 模糊控制系统的转速阶跃响应

4 结 语

本文给出了一种适用于超声波电动机转速控制的单输入T-S模糊控制器。从控制量表达式来看，该模糊控制器可看做一种变参数的PI控制器，只是其控制参数是通过在线模糊推理的方式来持续改变的。从模糊控制的角度来说，通过采用模拟PID控制的模糊控制器结构，通过在模糊控制器设计过程中利用实验整定的PID控制参数，简化了设计过程，减少了设计工作量和在线计算量。从PID控制的角度来看，所提控制器利用模糊推理过程的非线性机制，为提高PID控制参数拟合特性与超声波电动机非线性特性之间的匹配程度提供了可能。

[1] 赵淳生.超声电机技术与应用[M].北京：科学出版社,2007.

[2] 史敬灼.超声波电机运动控制理论与技术[M].北京：科学出版社.2011.

[3] 郑春娇,朱延枫.基于模糊PID的超声电机控制[J].辽宁工业大学学报(自然科学版),2011,31(2):95-98.

[4] 韩晓斌,于明礼.基于模糊免疫PID的超声电机控制[J].机械科学与技术,2015,34(10):1614-1620.

[5] 王珺,孙志峻.基于模糊神经网络的直线超声电机自适应控制[J].微电机,2013,46(1):41-45.

[6] 吕琳,史敬灼.基于蚁群优化的超声波电动机系统动态模糊辨识建模[J].微特电机,2011,39(10):58-60.

Single-Input Takagi-Sugeno Fuzzy Speed Controller of Traveling Wave Ultrasonic Motor

ZHANGMeng,SHIJing-zhuo

(Henan University of Science and Technology,Luoyang 471023,China)

The operation process of ultrasonic motor has obvious nonlinearity. So designing an appropriate motor control strategy is an important premise for the wider application of ultrasonic motor. A single-input Takagi-Sugeno fuzzy controller which is suitable for ultrasonic motor′s speed control was presented. Compared with the conventional fuzzy controller, the controller designed in experiments has simple structure which will reduce the workload and online computation amount. Experiments show that the control performance is better.

ultrasonic motor; speed control; fuzzy control; Takagi-Sugeno

唐慧雨(1992-)，男，硕士研究生，研究方向为电力电子与电力传动技术。

2015-12-31

国家自然科学基金项目(U1304501)

TM359.9

A

1004-7018(2017)01-0055-03