完全互补小波噪声辅助集总经验模态分解
何 刘, 丁建明, 林建辉, 刘新厂
(西南交通大学 牵引动力国家重点实验室, 成都 610031)
完全互补小波噪声辅助集总经验模态分解
何 刘, 丁建明, 林建辉, 刘新厂
(西南交通大学 牵引动力国家重点实验室, 成都 610031)
经验模态分解(EMD)是一种自适应非线性非平稳数据处理方法。噪声辅助的EMD方法能克服EMD方法在处理间歇信号时出现的“模态混叠”现象。在这些噪声辅助方法中,互补集总经验模态分解(CEEMD)和完全噪声辅助噪声集总经验模态分解(CEEMDAN)恢复了EMD分解的完整性。在现有分析方法上提出了完全互补小波噪声辅助集总经验模态分解(CCWEEMDAN)算法。该算法能用更小的集总数、更少的迭代次数和极小的计算消耗获得更好的光谱分离效果和数目较少的筛选模态。
经验模态分解;集合经验模态分解;噪声辅助;模态混叠;互补集总经验模态分解
经验模式分解(Empirical Mode Decomposition,EMD)[1-2]是一种非线性非平稳信号自适应分解的信号处理方法。该方法能根据数据自身的时间尺度自适应的将信号分解成具有实际物理意义的各个本征模态函数(Intrinsic Mode Function,IMF)分量和分解残差,将所有模态函数和最终趋势相加能完美重构原始数据。
EMD方法本身也存在一些问题,例如同一模态中出现不同尺度或频率的信号,或者同一尺度或频率的信号被分解到多个不同的模态中,该问题被称为“模态混叠”[3]。为了克服EMD方法的“模态混叠”问题,集总经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法被提出。通过在分解前添加高斯白噪声至原始信号中,利用高斯白噪声的频谱均匀分布特性和EMD方法的二进滤波特性填充整个时频空间[4],有效的解决了模态混叠问题。EEMD方法在解决模态混叠问题的同时却产生了新的问题。①由于EEMD方法添加了不同量级的高斯白噪声,最终分解可能得到不同数量的模态;②由于添加高斯白噪声的原因,使得分解得到的各个模态和最终趋势中存在噪声,这使得该方法不能精确重建原始数据。③由于高斯白噪声的引入需要相应集总次数的EMD分解求平均以抵消噪声影响,使得迭代次数增加、计算效率下降。
针对EEMD方法不能精确重建的问题,互补集总经验模态分解(Complementary Ensemble Empirical Mode Decomposition,CEEMD)[5]通过向待分析信号添加成对相反的高斯白噪声减小由白噪声引起的重构误差,并且提高了EEMD的计算效率。然而该方法依然不能解决添加不同噪声的信号产生不同数量模态分解的问题。完全噪声辅助集总经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)[6]的提出是对EEMD方法的重要发展,该方法实现了分解信号的近似完美重构以及解决了不同加噪信号产生不同数量模态的缺陷。尽管如此,CEEMDAN依然存在迭代次数多,计算效率低的问题。本文主要解决问题就是减少CEEMDAN方法的迭代次数,提高计算效率。
1 EMD, EEMD, CEEMD and CEEMDAN理论
EMD将信号分解为若干个基本模式分量IMF和一个余项。基本模式分量必须满足两个基本:①在数据列中,数据的极值点数量和过零点数量必须相等或最多相差一个;②任何一点,极大值和极小值的包络的平均值为0。该算法的详细过程为
步骤1 令k=0,计算信号r0=x的极大值和极小值。
步骤2 采用三次样条对信号rk所有极大值点、极小值点进行插值得到上下包络emax(emin)。
步骤3 计算并得到上下包络的平均值m=(emax+emin)/2。
步骤4 根据式(1)计算固有模态函数
rk-m=hk+1
(1)
步骤5 判断hk+1是否满足IMF的条件,如果不满足,对hk+1重复步骤2~步骤4得到满足条件的包络平均值。
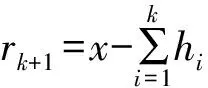
步骤7 重复上述步骤知道得到满足停止条件的最终趋势项rk。
EEMD分解的计算框架和EMD分解基本相同,将原始信号x筛分为IMF。在信号x筛分过程中添加不同白噪声ω(i)(i=1,…,I),I为集总次数,为每次EMD分解后剩余分量的时域分布提供一致的参考结构。其具体分解步骤为
步骤1 对原始数据添加白噪声,形成总体分解信号,其(i)中ε>0。
x(i)=x+εω(i)
(2)
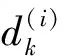
(3)
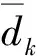
(4)
为解决EEMD存在的重构误差,YEH等提出了CEEMD方法。噪声被成对(一正一负)的添加到原始数据中进行两次集总分解。
(5)
(6)
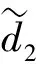
步骤1 在每次集总数i=1,…,I对信号x(i)=x+β0ω(i)进行EMD分解,得到第一阶模态。
(7)
步骤2 利用式(6)计算第一阶(k=1)残差r1。
步骤3 给第一阶残差添加噪声β1E1(ω(i)),得到分解输入信号r1+β1E1(ω(i)),(i=1,…,I),再进行EMD分解得到该信号的第一阶模态也就是原信号的第二阶模态。
(8)
步骤4 对于k=2,…,K的k阶残差为
(9)
步骤5 计算信号rk+βkEk(ω(i)),(i=1,…,I),的第一阶模态得到原始信号的第k+1阶模态。
(10)
步骤6 回到步骤4计算下一第k阶模态。
该方法停止规则为残差不能再进行EMD分解。
最终趋势项为
(11)
其重构公式为
(12)
该方法由于每一阶分解的初始信号均相同 (rk),并且只需要得到一阶模态,所以确保了不同集总数下均有相同数量的模态(模态数为1),并且该方法具有完美的重构误差。
但是该方法在处理一些信号时会出现同一模态的伪分量出现在固有模式前后,并且分解模态中依然包含残留噪声。基于这些问题文献[7]又对CEEMDAN方法做了进一步的改进。从原始CEEMDAN中可以发现,首先是第一阶模态求解时直接向信号中添加了高斯白噪声,而第二阶求解中却添加的是经过EMD分解后的噪声,这使得每一阶求解中出现噪声的交叉干扰,改进方法将第一阶模态求解时信号添加噪声修改为一阶EMD分解得到的噪声,其它阶模态求解添加的噪声是相应阶次EMD分解后的噪声。其次原方法每次求解模态分量时均对模态函数求平均以消除噪声的影响,但是每次添加的噪声频带均和分解出的固有模态频带重合,实际添加的噪声被大量分解在了模态函数中。然而,信号分解残差的频带小于分解出的模态函数频带,相应的也小于添加噪声的频带。因此分解到残差中的噪声最小,最容易被平均,所以改进方法是将原来求解模态函数均值修改为求解残差均值,而模态函数有分解信号减去残差均值得到。定义算子M(·)为计算EMD第一阶模态后的残差信号。改进后的方法具体算法步骤为
步骤1 计算信号x(i)=x+β0E1(ω(i))(i=1,…,I)第一阶残差信号
(13)
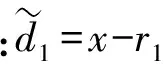
步骤3 第一阶残差中添加噪声β1E2(ω(i)),按照步骤1和步骤2求解第二阶模态
(14)
步骤4 对于k=3,…,K的k阶残差为
(15)
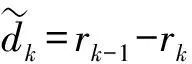
步骤6 回到步骤4计算下一阶模态。
其分解的每一阶噪声信噪比均能选择βk=εkstd(rk)。
2 完全小波噪声辅助集总经验模态分解和完全互补小波噪声辅助集总经验模态分解
详细分析CEEMDAN算法发现,在每阶残差信号中均添加特定的噪声信号βkEk(ω(i)),该噪声是通过EMD分解得到,那么CEEMDAN方法实际的迭代计算次数Nreal为
Nreal=Nx+Nnoise
(16)
式中:Nx为计算各阶模态的迭代次数;Nnoise为计算各阶噪声的迭代次数。利用CEEMDAN分析如下仿真信号x。
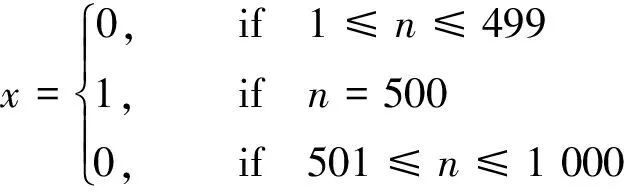
(17)
CEEMDAN方法分析该仿真信号,计算实际模态的迭代次数箱型图为图1,计算各阶噪声的迭代次数箱型图为图2。图中可以看出计算各阶噪声花费的计算量也非常巨大。所以该方法的实际迭代次数为前两者迭代次数的总和,其箱型图为图3所示。
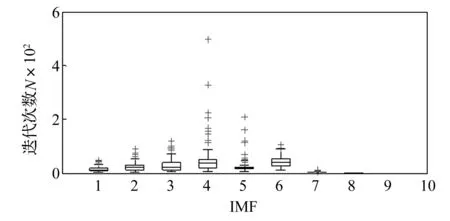
图1 计算各阶模态的迭代次数Fig.1 The iteration number of each mode
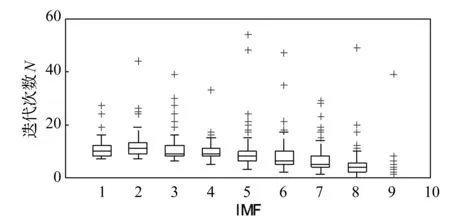
图2 计算各阶噪声的迭代次数Fig.2 The iteration number of each noise

图3 完整CEEMDAN的实际迭代次数Fig.3 The actual iteration number of complete CEEMDAN
在本组分解中计算各阶模态函数花费的总迭代次数为Nx=19 735次,计算各阶噪声的总迭代次数为Nnoise=7 376次,该方法实际总迭代次数为Nreal=27 111次,噪声迭代次数约占比实际总迭代次数的27%,相应的计算各阶模态函数的迭代次数约占比实际总迭代次数的73%,并且分解层数越少则花费在噪声分解中的迭代次数占比会急剧上升。
单独分析EMD方法对高斯白噪声的分解性质,设定20 000个独立的高斯白噪声数据(其中均值为0,方差为1),对每个高斯白噪声数据进行EMD分解得到不同的IMF分量,计算每个分量的功率谱。计算20 000个信号对应功率谱的平均值并进行幅值归一化,计算结果为EMD的等效滤波特性。具体如图 4所示,其横坐标化为了角频率并做了归一化。
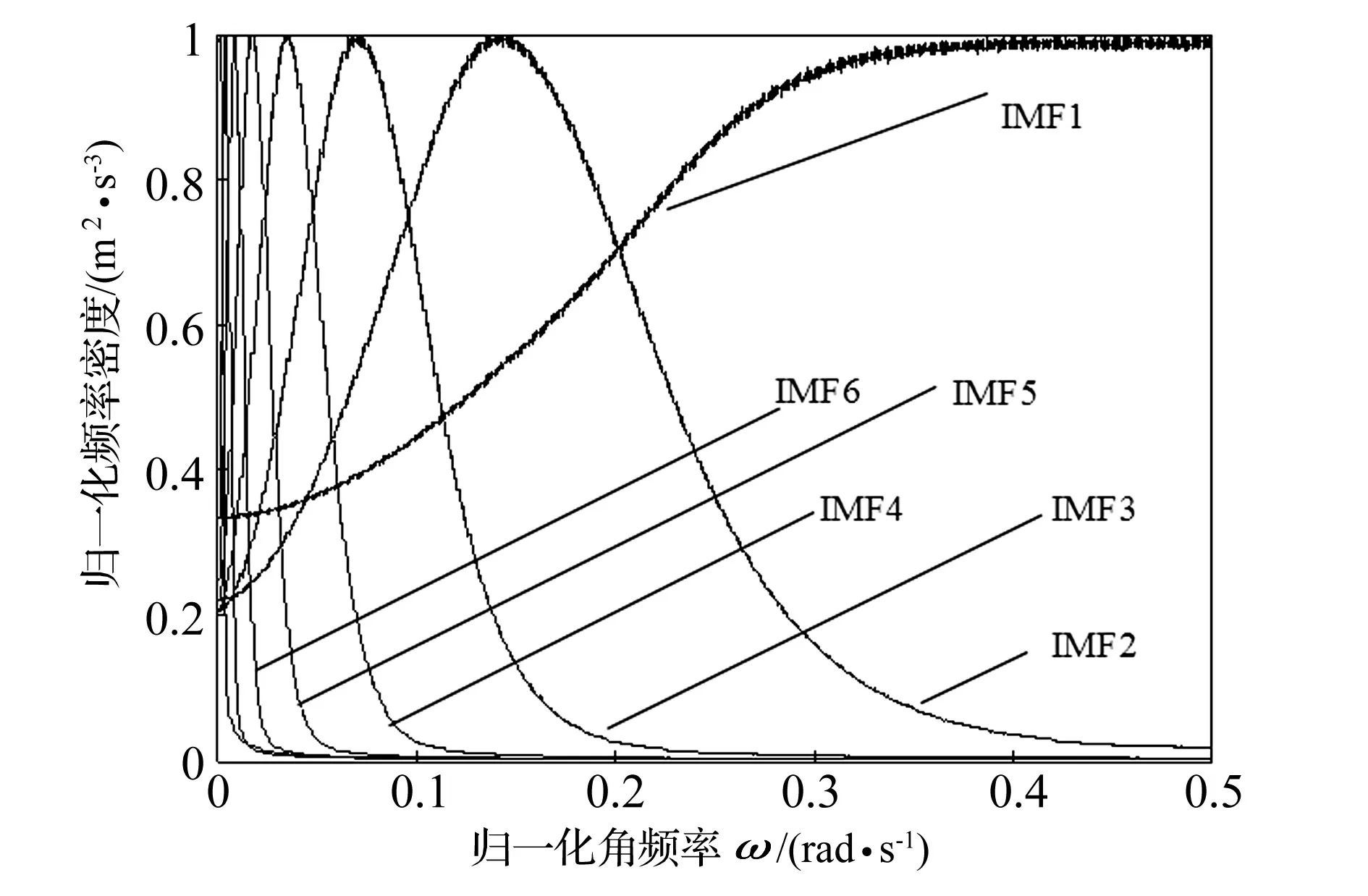
图4 EMD的等效滤波特性Fig.4The equivalent filter characteristics of EMD
分析图4可得出,白噪声被EMD规律性的分解为能量均匀分布的各频率分量,EMD表现出有效的二元滤波器组特性。而小波分解也具有相似的特征,由Mallat算法可知,二进小波分解对信号频带划分也表现为二元滤波器组特性。本文用coif3小波分解高斯白噪声得到小波分解的等效滤波特性如图5所示。对比图4和图5发现coif3小波和EMD方法对白噪声的频带划分同样表现为二元滤波器组特性。
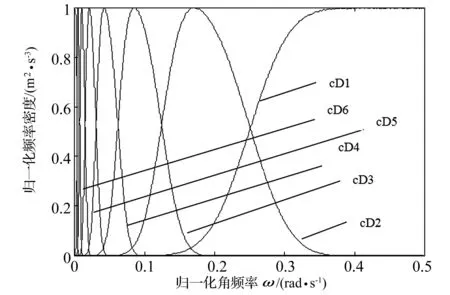
图5 小波的等效滤波特性Fig.5 The equivalent filter characteristics wavelet
正是基于小波分解和EMD分解均表现为相同滤波特性的特点,可将CEEMDAN分解中求解各阶添加噪声的EMD算法改为小波分解代替,以达到在继承CEEMDAN优良特性的基础上减少算法迭代次数提高计算效率的目的。新方法为完全小波噪声辅助集总经验模态分解,定义算子Wj(·)是通过小波计算给定信号j层小波分解并单子重构第j个细节信号的算子,算子M(·)为用EMD求解一阶模态后的残差信号的算子,同样高斯白噪声为ω(i)(i=1,…,I),I为集总次数。CWEEMDAN方法详细计算步骤流程为
步骤1 在信号x添加I个噪声,即x(i)=x+β0W1(ω(i))(i=1,…,I),对每组信号进行一层EMD分解得到I个残差,平均后得到第一阶残差分量。
(18)
步骤3 第一阶残差r1叠加I个噪声信号β1W2(ω(i)),并计算第二阶残差。
(19)
步骤5 对于k=3,…,K的k阶残差为
(20)
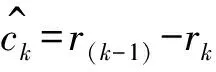
步骤7 回到步骤5计算下一阶模态。
此外,详细分析上诉算法发现CWEEMDAN还可以根据CEEMD方法中减小添加噪声影响的方法,将CWEEMDAN中每次添加的特定的噪声信号βkEk(ω(i))正负成对的添加到分解信号中以达到进一步的减小添加噪声的影响,最终达到在求解相同分解结果时,减少集总次数。所以最终改进算法为完全互补小波噪声辅助集总经验模态分解,算法的具体步骤如下(见图6)。

图6 CCWEEMDAN算法流程图Fig.6 Flowchart describing the CCWEEMDAN
同样高斯白噪声为ω(i)(i=1,…,I/2),I(偶数)为集总次数。
步骤1 在信号x添加I/2对噪声,对每组信号进行一层EMD分解得到I个残差,平均后得到第一阶残差分量
(21)
(22)
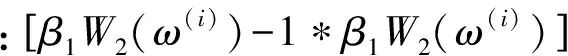
(23)
(24)
步骤5 对于k=3,…,K的k阶残差为
(25)
(26)
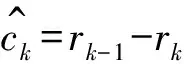
步骤7 回到步骤5计算下一阶模态。
3 EMD, EEMD, CEEMD ,CEEMDAN,CWEEMDAN and CCWEEMDAN分解性能比较
为对比EMD,EEMD,CEEMD,CEEMDAN CWEEMDAN和CCWEEMDAN方法分解性能,构造仿真信号:s=s1+s2。
(27)
(28)
该仿真信号及各组成成分的时域波形图如图7所示。用以上涉及的六种方法对该组信号进行分解,噪声辅助EMD分解方法的集总数为50,噪声水平为0.2,分解结果如图8所示。

图7 仿真信号及其各组成成分波形图Fig.7 The waveforms of simulation signal and its components
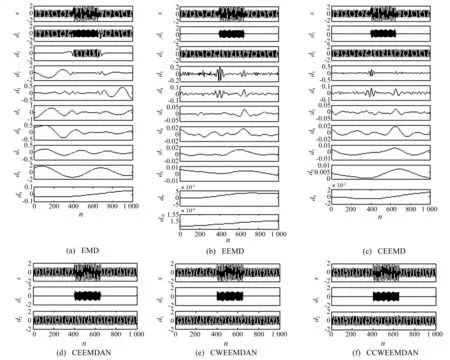
图8 仿真信号EMD,EEMD,CEEMD,CEEMDAN,CWEEMDAN和CCWEEMDAN分解结果Fig.8 Decomposition of artificial signals by EMD,EEMD,CEEMD,CEEMDAN,CWEEMDAN and CCWEEMDAN
对比图8的结果发现,EMD分解存在严重的模态混叠,未能将间歇信号s1和谐波信号s2完整分解开。而剩下的四种噪声辅助方法均将两个分量信号完整分解开来,避免了模态混叠。但是EMD,EEMD和CEEMD方法分解出了9个或以上的模态,虽然从第三个模态开始具有很小的能量,但是并不代表原始信号的信息。而CEEMDAN CWEEMDAN和CCWEEMDAN方法可以在分解的每一阶验证全局的停止准则,一旦满足IMF条件,整体分解很快停止。噪声辅助的EMD分解具有一定随机性,对于同一组信号同样两次的分解结果稍有不同。此外,随着集总数的增加,分解的残余噪声能量应当进一步减小,为量化该性能指标,在集总数I=50,100,200,400,800时用上述方法中的五种噪声辅助方法(EEMD,CEEMD,CEEMDAN,CWEEMDAN,CCWEEMDAN)对仿真信号进行100次分解,其中噪声幅度ε=0.2。
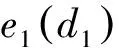
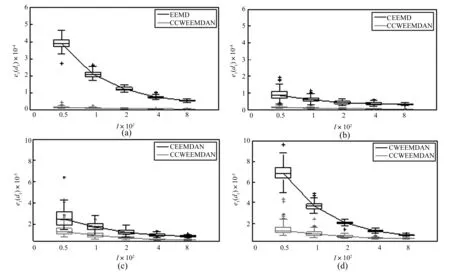
图9 五种噪声辅助EMD方法对仿真信号s的分解性能Fig.9 Performances of the five noise-assisted methods on artificial signal s
为比较分析方法对原始信号各分量的恢复能力,定义恢复信号a和基准信号b的相对平方根误差为
(29)
对已知分量信号的恢复性能分析(见图10和图11),CWEEMDAN比EEMD,CEEMD,CWEEMDAN的结果均要好,而CWEEMDAN在集总次数<100时的结果也优与CEEMDAN。当集总次数>200时CEEMD,CEEMDAN,CWEEMDAN和CCWEEMDAN的恢复性能不随集总次数的提高而提高,而CEEMDAN方法在集总次数大于200时的恢复性能略优于CCWEEMDAN,这是因为在集总次数足够大时大部分噪声几乎被平均,而由小波滤波特性与EMD滤波特性的差异引起的噪声未被完全平均。
对比CEEMDAN和CCWEEMDAN的恢复性能可以发现,虽然在集总次数非常大时,CEEMDAN具有比CCWEEMDAN较好的恢复性能,但是其相差不大,几乎不会对结果有影响,并且CCWEEMDAN具有在低集总次数得到高恢复性能的优点。最后,对五种方法的信号重构性能做对比分析(见图12),CCWEEMDAN重构性能均优于EEMD,CEEMD和CWEEMDAN,并且重构误差和CEEMDAN达到了同一数量级10-17。CCWEEMDAN和CEEMD比较发现随着集总次数的增加重构误差变大,其原因是加入不同噪声会使信号产生不同数量的模态,随着集总次数的增加产生不同数量模态的概率增加,所以重建误差增大。
五种噪声辅助方法对仿真信号每次EMD分解的平均迭代次数如图13所示。比较四副图发现,CCWEEMDN方法比其它四种方法具有更少的迭代次数,更低的计算消耗。为进一步比较五种噪声辅助EMD方法的计算开销,使用一组真实数据对五种方法进行验证,该数据来源于MIT-BIH正常窦性心律的心电图(ECG)信号。对该组心电信号进行五种噪声辅助EMD方法的分解(集总数为100,噪声幅度为0.2),其中EEMD、CEEMD、CEEMDAN和CWEEMDAN方法筛选各阶模态需要的迭代次数如图14所示,而本文最终提出的CCWEEMDAN方法筛选各阶模态的迭代次数如图15所示。比较图14和图15可知,EEMD和CEEMD方法
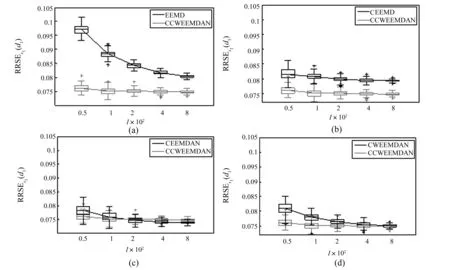
图10 五种噪声辅助EMD方法对仿真信号s1的恢复性能Fig.10 Performances of the five noise-assisted methods on artificial signal s1
计算各阶模态的迭代次数最多,并且这两种方法得到的模态也最多;CEEMDAN方法和CWEEMDAN、CCWEEMDAN方法得到的模态数量均较少,但是CEEMDAN方法筛选各阶模态的迭代次数均大于后两种新的算法。五种噪声辅助EMD方法单次EMD分解的迭代次数如图16所示。由图16可知,迭代次数最多的EEMD和CEEMD,它们单次EMD分解最大概率的迭代次数分别为543次和529次,CEEMDAN单次EMD分解最大概率的迭代次数为356次,迭代次数最少的是CWEEMDAN和CCWEEMDAN,其迭代次数分别为238次和240次。通过计算可知,CEEMDAN方法计算效率大约是EEMD和CEEMD的1.5倍;CWEEMDAN和CCWEEMDAN计算效率大约是CEEMDAN的1.5倍;总体而言新噪声辅助EMD方法的计算效率大约是原始EEMD方法的2.25倍。如果考虑到单次EMD分解中的异常迭代次数,集总次数为100次的EEMD迭代次数为65 729次,CEEMD总迭代次数为62 918,CEEMDAN总迭代次数为39 937次,CWEEMDAN和CCWEEMDAN总迭代次数分别为25 594次和26 978次(见图 17)。分析图17可知,CCWEEMDAN总迭代次数仅仅是CEEMDAN的67.55%,是CEEMD的42.84%,是EEMD的41.04%,几乎和CWEEMDAN持平。
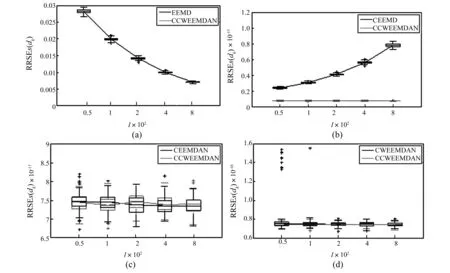
图12 五种噪声辅助EMD方法重构性能Fig.12 Performances of the five noise-assisted methods on artificial signal s: reconstruction error
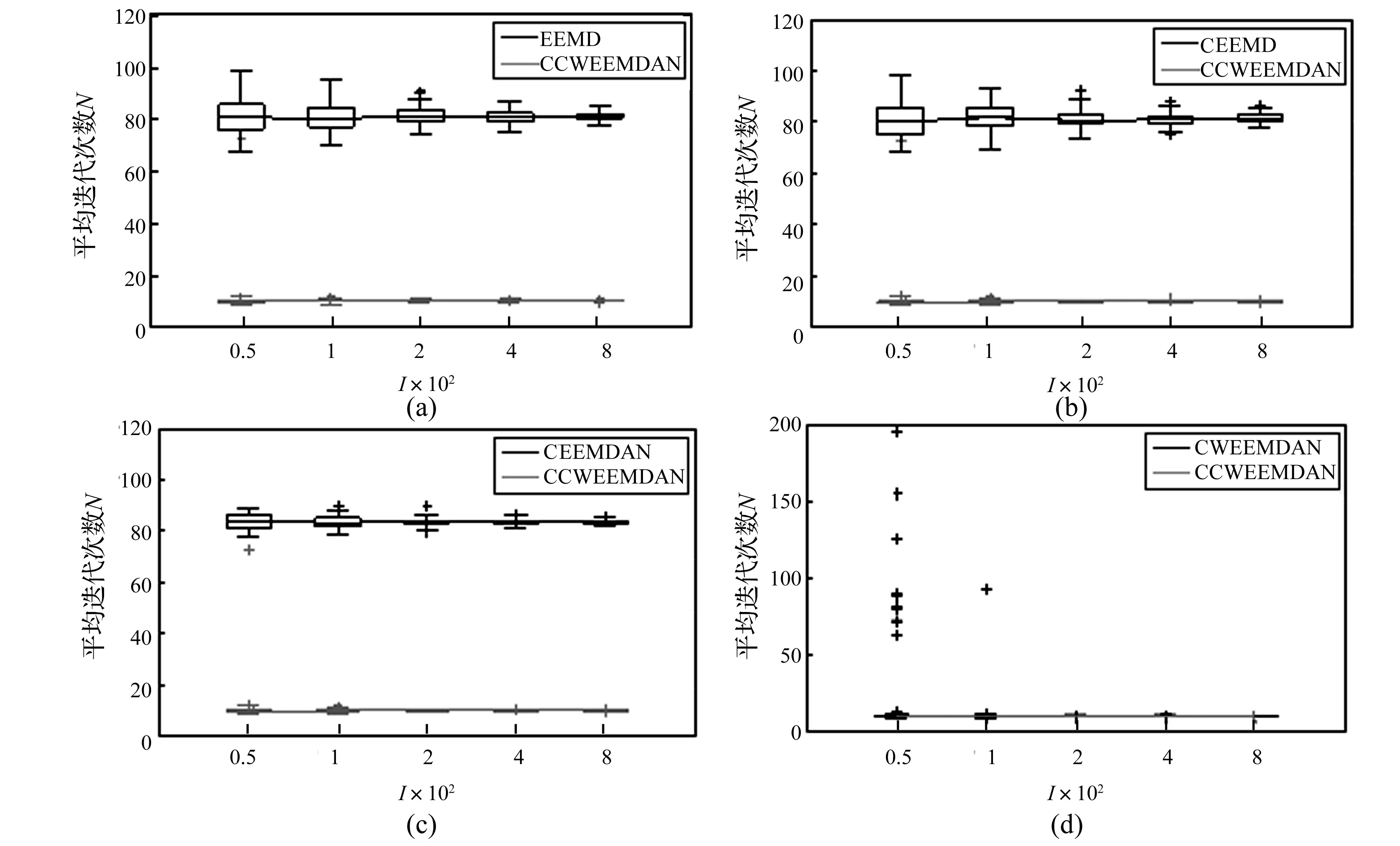
图13 五种噪声辅助EMD方法平均迭代次数Fig.13 The average number of iterations of five noise-assisted methods
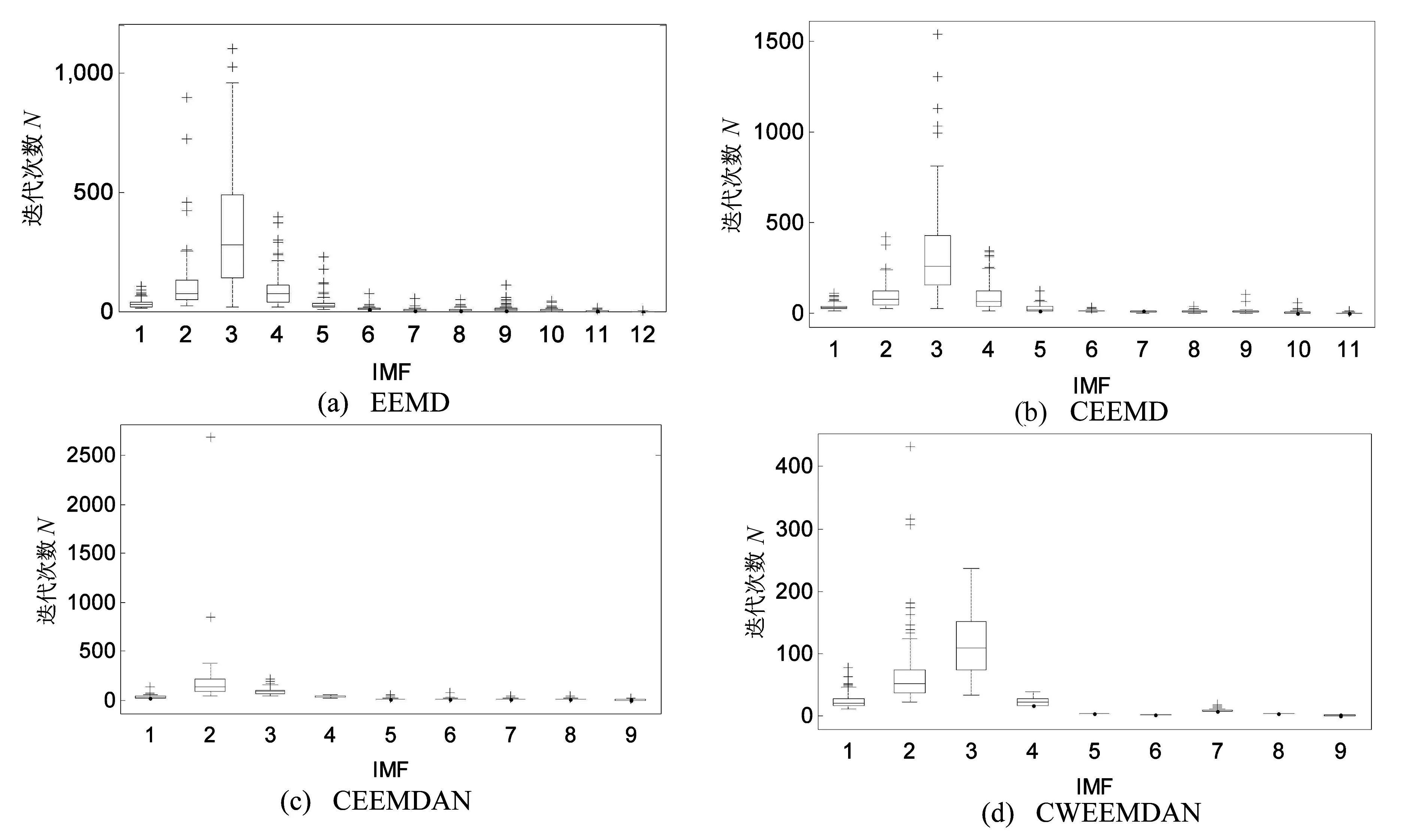
图14 EEMD,CEEMD,CEEMDAN和CWEEMDAN刷选各阶模态的迭代次数Fig.14 The iteration number of each mode by EEMD, CEEMD, CEEMDAN and CWEEMDAN
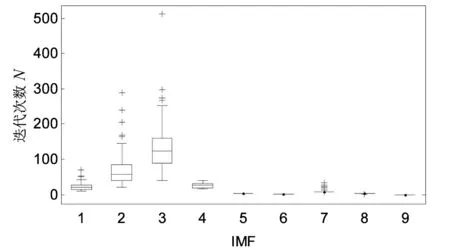
图15 CCWEEMDAN筛选各阶模态的迭代次数Fig.15 The iteration number of each mode by CCWEEMDAN
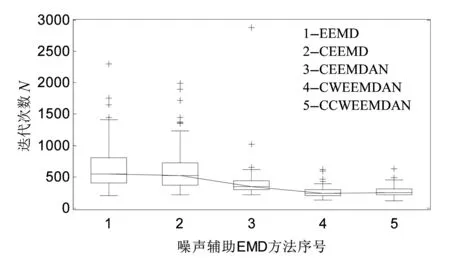
图16 五种噪声辅助EMD方法单次EMD分解的迭代次数Fig.16 The sifting iterations for each mode of the five noise-assisted methods
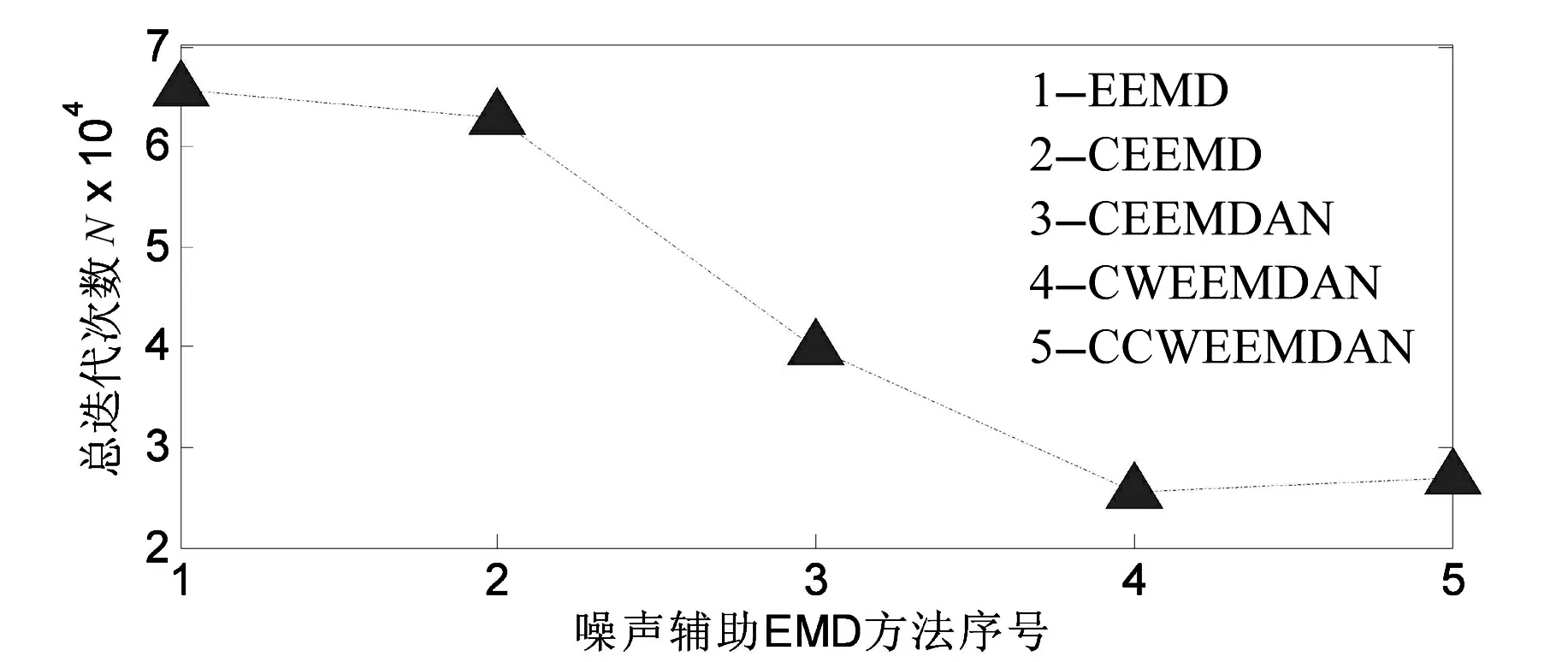
图17 五种噪声辅助EMD方法总迭代次数Fig.17 The total iterations of five noise-assisted methods
五种噪声辅助EMD方法的重构误差如图18所示,除EEMD外其余四种噪声辅助EMD方法的重构误差均小于5×10-13。比较后四种方法的重构误差平方和(如图19),CCWEEMDAN的重构误差平方和最小。
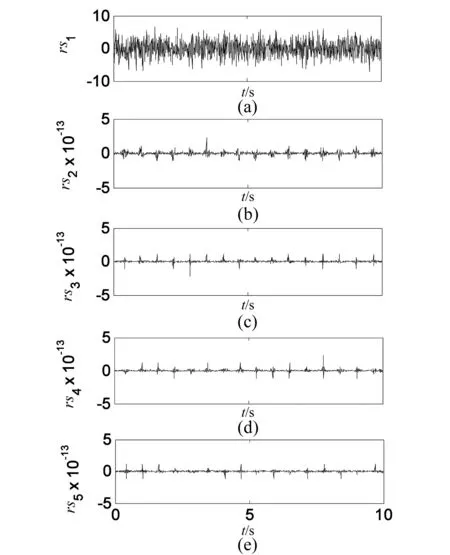
图18 五种噪声辅助EMD方法重构误差Fig.18 The reconstruction error of five noise-assisted methods
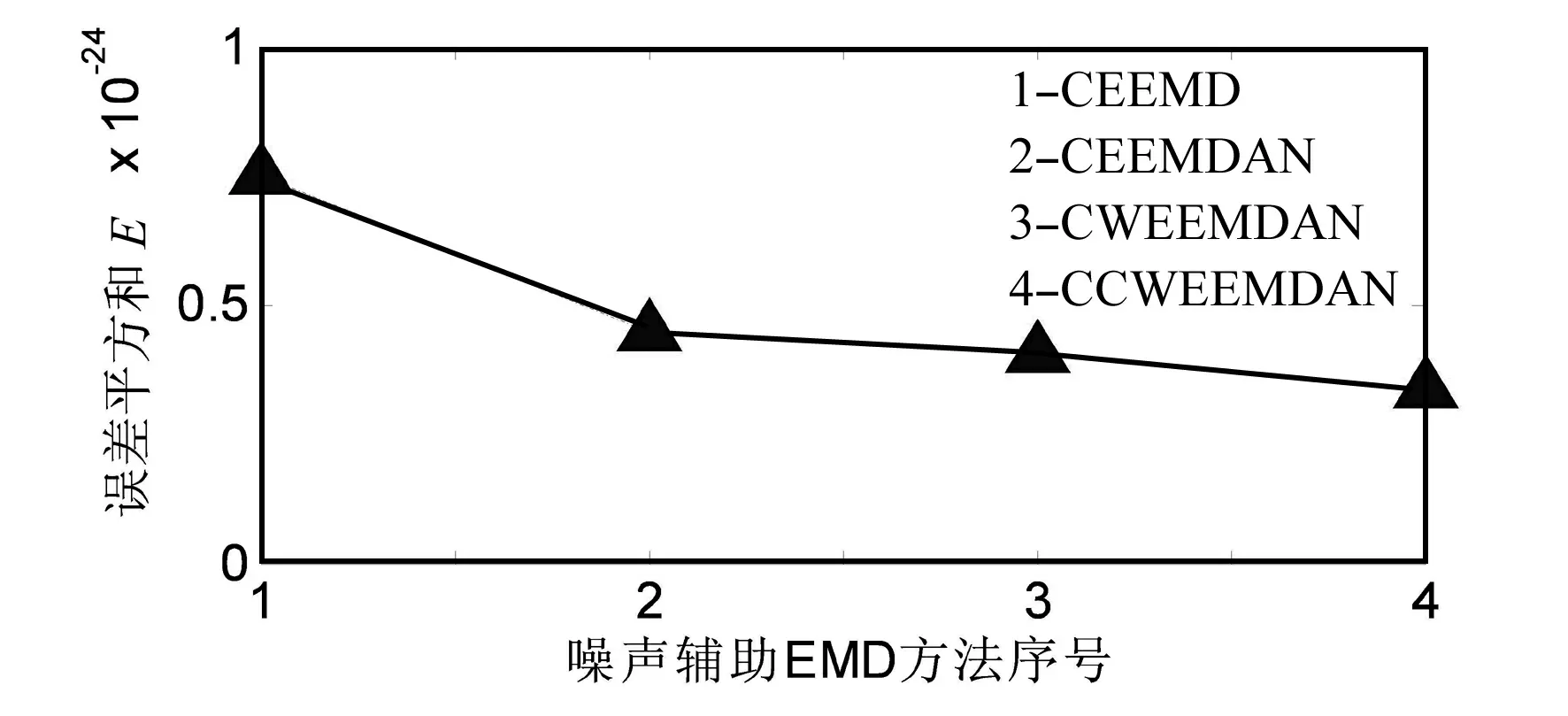
图19 四种噪声辅助EMD方法重构误差平方和Fig.19 The quadratic sum of reconstruction error of four noise-assisted methods
4 结 论
本文提出了非线性、非平稳信号处理新算法,新算法对仿真信号和实测信号具有很好的测试效果。新方法(CCWEEMDAN)概括起来具有以下特点:
(1)CCWEEMDAN同EEMD一样具有抗频率混叠的特性。
(2)CCWEEMDAN比EEMD和CEEMD具有更少的伪模态数量。
(3)CCWEEMDAN比EEMD和CEEMD有更小的残余噪声和重构误差,以较小集总次数获得比CEEMDAN更好的分解效果和重构精度。
(4)CCWEEMDAN较其它噪声辅助方法具有更小的迭代次数和计算开销。
[1] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis [J]. Proceedings of the Royal Society a Mathematical Physical & Engineering Sciences, 1998,454:903-995.
[2] HUANG N E,SHEN Z,LONG R S. A new view of nonlinear water waves the Hilbert spectrum [J].Annual Review of Fluid Mechanics,1999,31(1): 417-457.
[3] WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise-assisteddata analysis method [J]. Advances in Adaptive Data Analysis, 2009,1 (1):1-41.
[4] FLANDRIN P, RILLING G, GONCALVS. Empirical mode decomposition as a filter bank [J]. IEEE Signal Processing,Letters,2004,11(2):112-114.
[5] YEH J R, SHIEH J S, HUANG N E, Complementary ensemble empirical modedecomposition: a novel noise enhanced data analysis method [J]. Advances in Adaptive Data Analysis,2010,2 (2):135-156.
[6] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise [J]. Brain Research Bulletin, 2011,125(3):4144-4147.
[7] COLOMINAS M A, SCHLOTTHAUER G, TORRES M E. Improved complete ensemble EMD: a suitable tool for biomedical signal processing [J]. Biomedical Signal Processing and Control,2014,14(1):19-29.
A complete complementary wavelet ensemble empirical mode decomposition with adaptive noise
HELiu,DINGJianming,LINJianhui,LIUXinchang
(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)
Empirical mode decomposition (EMD) is a self-adaptive method and suitable to analysing the non-stationary and nonlinear signals. Noise-assisted versions have been proposed to alleviate the so-called “mode mixing” phenomenon, which may appear when an EMD algorithm is used to deal with a signal with intermittency. Among them, the complementary ensemble EMD (CEEMD) and complete ensemble EMD with adaptive noise (CEEMDAN) recover the completeness property of EMD. In this work a new algorithm named complete complementary wavelet ensemble empirical mode decomposition with adaptive noise(CCWEEMDAN) was presented based on those existing techniques, obtaining better spectral separation of the modes with fewer sifting iterations and less noise of components with small ensemble number and extremely low computational cost.
empirical mode dercompostion; ensemble empirical mode decomposition; noise-assisted data analysis; mode mixing; complementary ensemble empirical mode decomposition
国家自然科学基金项目(61134002; 51305358)
2015-09-09 修改稿收到日期:2016-01-04
何刘 男,硕士生,1990年生
丁建明 男,博士,助理研究员,1981年生
U211;U270
A
10.13465/j.cnki.jvs.2017.04.037

