基于子结构的有限元模型修正方法

翁 顺， 左 越， 朱宏平， 陈 波， 赵会贤， 田 炜， 颜永逸

(1.华中科技大学 土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074； 2.武汉理工大学 土木工程与建筑学院，武汉 430070)

基于子结构的有限元模型修正方法

翁 顺1， 左 越1， 朱宏平1， 陈 波2， 赵会贤1， 田 炜1， 颜永逸1

(1.华中科技大学 土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074； 2.武汉理工大学 土木工程与建筑学院，武汉 430070)

提出了一种基于子结构的有限元模型修正方法。该方法将整体结构有限元模型划分为多个子结构模型，求解独立子结构的主模态特征解和特征灵敏度；通过位移协调条件和能量方程，约束相邻独立子结构，得到整体结构的特征解和特征灵敏度；并以整体结构模态和结构试验模态的残差为目标函数，通过调整子结构单元参数，完成有限元模型修正。当结构局部参数发生变化，通过分析某一个或几个子结构即可求解整体结构特征解和特征灵敏度，而不需要分析其他未发生变化的子结构。由于子结构模型尺寸远小于整体结构，该方法能够极大地提高有限元模型修正方法的精度和效率。

有限元模型修正; 损伤识别; 子结构；特征解; 特征灵敏度

精确的有限元模型是结构健康评估、动态分析以及优化设计的基础。建模过程中参数的不确定性、边界条件的假定等，导致有限元模型的动态响应和实测的试验数据存在误差。设计规范规定, 有限元模型必须通过振动模态试验或者地面共振试验来检验。因此，近年来, 有限元模型修正技术得到了长足的发展[1-8]。根据修正对象的不同可将修正方法分为矩阵型方法和设计参数型方法。前者直接重建分析模型的刚度和质量矩阵。后者重复的修正有限元模型的物理参数来使模型的模态特性(频率和振型)和现场试验模态的残差最小化。设计参数型方法物理意义明确，并且修正后的系统矩阵在对称性、正定性和稀疏性等方面与修正前的矩阵保持一致。其中，基于灵敏度分析的设计参数型修正方法为模型修正过程提供有效地优化搜索方向，效率高，被广泛的应用于实际工程结构中[9-13]。

大多数设计参数型修正方法采用优化技术，通过重复计算模型的特征解和特征灵敏度矩阵，寻找最接近实际工程结构的物理参数，实现模型修正过程。但是，土木工程结构体积庞大，为了有效地模拟实际工程结构，其有限元模型通常由大量的单元组成，并且包含许多需要被修正的结构设计参数，优化迭代过程通常需要花费很多时间，特别是从庞大的有限元模型的系统矩阵中重复计算特征解和特征灵敏度[14-16]。

子结构方法将庞大的整体结构分解为若干个较小的独立子结构，通过位移协调条件和力的协调条件建立整体结构和子结构之间的关系。由于独立子结构系统矩阵较小，未知参数少，在大型结构的模型修正及其相关应用中具有以下优势[17]： ①子结构系统矩阵较小，分析精度和效率高;②各子结构相互独立，可以对独立子结构进行修正和重新分析，不需要分析整体结构;③针对当前的多核计算机硬件，进行并行计算，提高计算效率。

本文研究基于子结构的有限元模型修正方法。该方法通过组集子结构主模态的特征解和特征灵敏度，求解整体结构的特征解和特征灵敏度，用于有限元模型修正。在计算整体结构对结构单元参数的特征灵敏度时，只需要计算包含该单元参数的一个子结构的特征灵敏度，其他子结构的特征灵敏度为0。由于子结构的尺寸远远小于整体结构，该子结构方法极大的提高结构特征值和特征灵敏度的计算效率，从而有效地提高了模型修正过程的效率。基于正向子结构的有限元模型修正方法应用于一个实际工程桥梁的有限元模型修正中，验证其精度和效率。

1 子结构方法求特征解

将N个自由度的整体结构分解为NS个子结构。以第j(j=1, 2, …,NS)个子结构为例，假如第j个子结构有n(j)个自由度，刚度矩阵为K(j)，质量矩阵为M(j)，其n(j)对特征值和特征向量为

[Φ(j)]TK(j)Φ(j)=Λ(j)

[Φ(j)]TM(j)Φ(j)=I(j)

(j=1, 2, …,NS)

(1)

KRON[18]的子结构方法基于虚功原理和几何相容性原则，通过在子结构相邻界面处施加约束，得到整体结构的特征方程为

(2)

其中，

Γ=[CΦp]T

Λp=Diag[Λ(1),Λ(2),…,Λ(NS)]

Φp=Diag[Φ(1),Φ(2),…,Φ(NS)]

(3)

从能量守恒的观点出发，全部子结构的所有阶模态都会对整体结构的特征模态有贡献，也就是说，要组装得到Λp和Φp需要计算全部子结构的所有阶特征解。实际工程结构往往只计算部分低阶模态，求解子结构的全部模态效率很低。为了克服这个困难，本文通过引入模态截断方法来提高KRON子结构方法的效率。选取每个子结构的低阶模态作为“主模态”，剩下的高阶模态作为“从模态”。在组装整体结构的特征方程时只需要计算主模态，从模态的能量贡献用剩余柔度来补充。

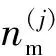
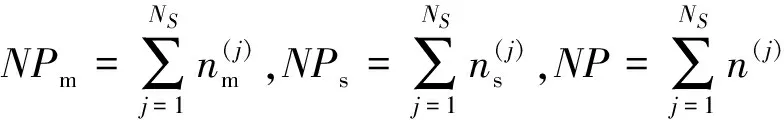
(j=1,2,…,NS)

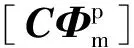
(4)

整体结构特征方程式(2)可以根据主模态和从模态重新分解为

(5)

根据式(5)的第二行，从模态的模态参与系数可以表示为

(6)

将式(6)代入式(5)中得到

(7)

(8)

(9)

式(9)的第二行将τ表示为zm，并且代入式(9)的第一行，可得到

(10)

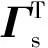
(11)

(12)

简化后的特征方程式(10)的尺寸等于NPm×NPm，远小于原始特征方程式(2)的尺寸NP×NP，因此将极大地提高子结构方法求解特征解的效率。

2 子结构方法求解特征灵敏度

本节以第R个子结构的第r单元参数为例，推导整体结构第i阶模态对参数r的特征灵敏度矩阵。式(10)用第i阶模态表示为

(13)

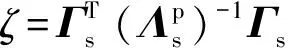
(14)

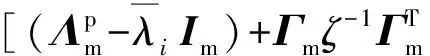
(15)

其中,

(16)

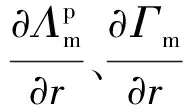
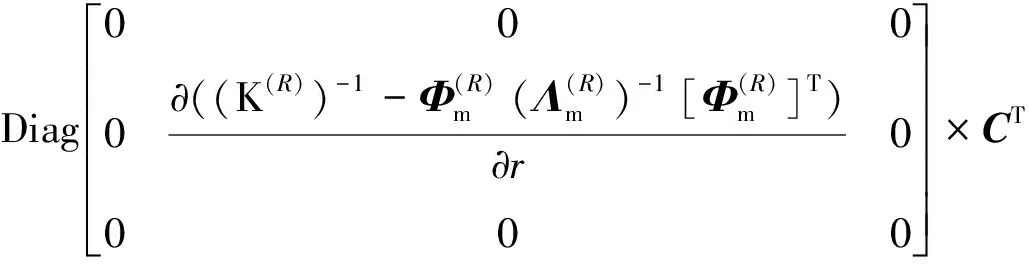
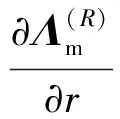
(18)

将式(18)对参数r求偏导，可以得到第i阶模态的特征向量灵敏度为

(19)

(20)

式中,ci为第i阶模态{zi}的参与系数。

将式(20)代入式(14)得

(21)

求解式(21)，得到常向量{vi}。

求解式(13)的特征解，特征向量{zi}满足正交条件

{zi}T{zi}=1

(22)

式(22)对r求偏导后得

(23)

将式(20)代入式(23)中，得到第i阶模态的参与系数ci为

(24)

求解到常向量{vi}和第i阶模态的参与系数ci后即可得到

(25)

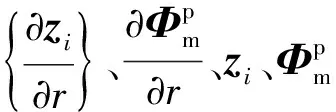
3 基于灵敏度分析的有限元模型修正方法

在基于灵敏度分析的模型修正过程中，将有限元模型的计算模态同结构试验模态的残差作为目标函数

(26)

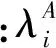
基于灵敏度分析的设计参数型修正方法，求解目标函数关于结构设计参数的灵敏度矩阵，提供最优的优化搜索方向。目标函数对结构设计参数的灵敏度矩阵为

(27)

其中特征值和特征向量对于参数r的灵敏度矩阵表示为

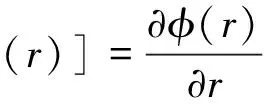
(28)

本研究采用子结构方法求解所有单元参数的一阶偏导。在有限元模型修正过程中，基于子结构方法通过式(26)构建目标函数，通过式(29)建立灵敏度矩阵为优化算法提供搜索方向，采用常用的基于Trust-region的优化算法，完成有限元模型修正过程。

4 工程应用

为了验证基于正向子结构的有限元模型修正方法在实际结构中的可行性和计算效率，将其应用于西澳大利亚的巴拉巴拉河大桥的有限元模型修正。根据设计图纸可以建立如图1所示有限元模型。该有限用模型的桥包含907个单元、947个节点。每个节点有6个自由度，共5 420个自由度。在现场的振动测试中，加速度计放置在7个纵梁对应的7列上，每列有19个测量点，共133个测量点。通过现场模态试验提取前10阶自振频率和振型(见图2)。

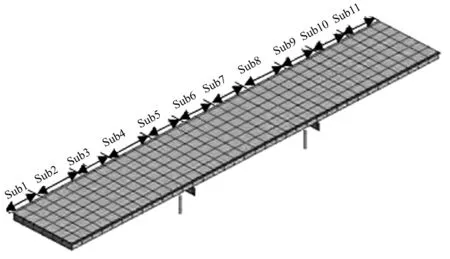
图1 Balla Balla Bridge有限元模型和子结构划分方法Fig.1 FE model of Balla Balla Bridge and the substructures

分别采用传统的基于整体结构的有限元模型修正方法和本文所提出的基于子结构的有限元模型修正方法对有限元模型进行修正。一共选取了包括膈、梁、板的杨氏模量(E)，剪力连接件的拉压刚度(EA)和抗弯刚度(EIxx,EIxy)在内的1 289个物理参数作为修正参数。目标函数根据式(26)定义为有限元模型的频率振型与试验模态的频率振型之间的残差。由于振型测量的误差大于频率，将振型的权重设定为0.1而频率的权重设定为1.0。

首先应用传统的整体结构有限元模型修正方法完成有限元模型修正。采用Lanczos方法从整体结构系统矩阵中计算结构特征解构建目标函数，用NELSON方法计算特征灵敏度用于提供优化搜索方向。由于试验模态只测到部分模态，在每次优化迭代中，计算有限元模型前30阶模态并与实测的前10阶模态进行匹配。通过模态置信准则MAC(Modal Assurance Creterion)

(29)

从有限元模型计算的30阶模态中找出与试验模态匹配的10阶模态。

模型修正过程迭代69次后收敛到预先设定的阈值，在普通个人电脑上每一步迭代大约花费1.26 h，模型修正过程共花费86.16 h，其收敛过程如图3所示。

然后，应用所提出的基于子结构的方法有限元模型修正方法完成有限元模型修正，并采用和上述整体结构方法相同的优化算法、修正参数、收敛准则等前提条件，并且在相同的个人电脑上运行程序。用本文所提出的子结构方法计算整体结构的特征值和特征灵敏度。将整体结构沿纵向分成11个子结构，如表1所示。每一步优化迭代过程中，通过组集独立子结构的特征值求解整体结构的特征值。计算整体结构对某一单元参数的特征灵敏度，只需要求解包含这个单元参数的一个子结构的主模态特征灵敏度，而其他的子结构的特征灵敏度设定为0。

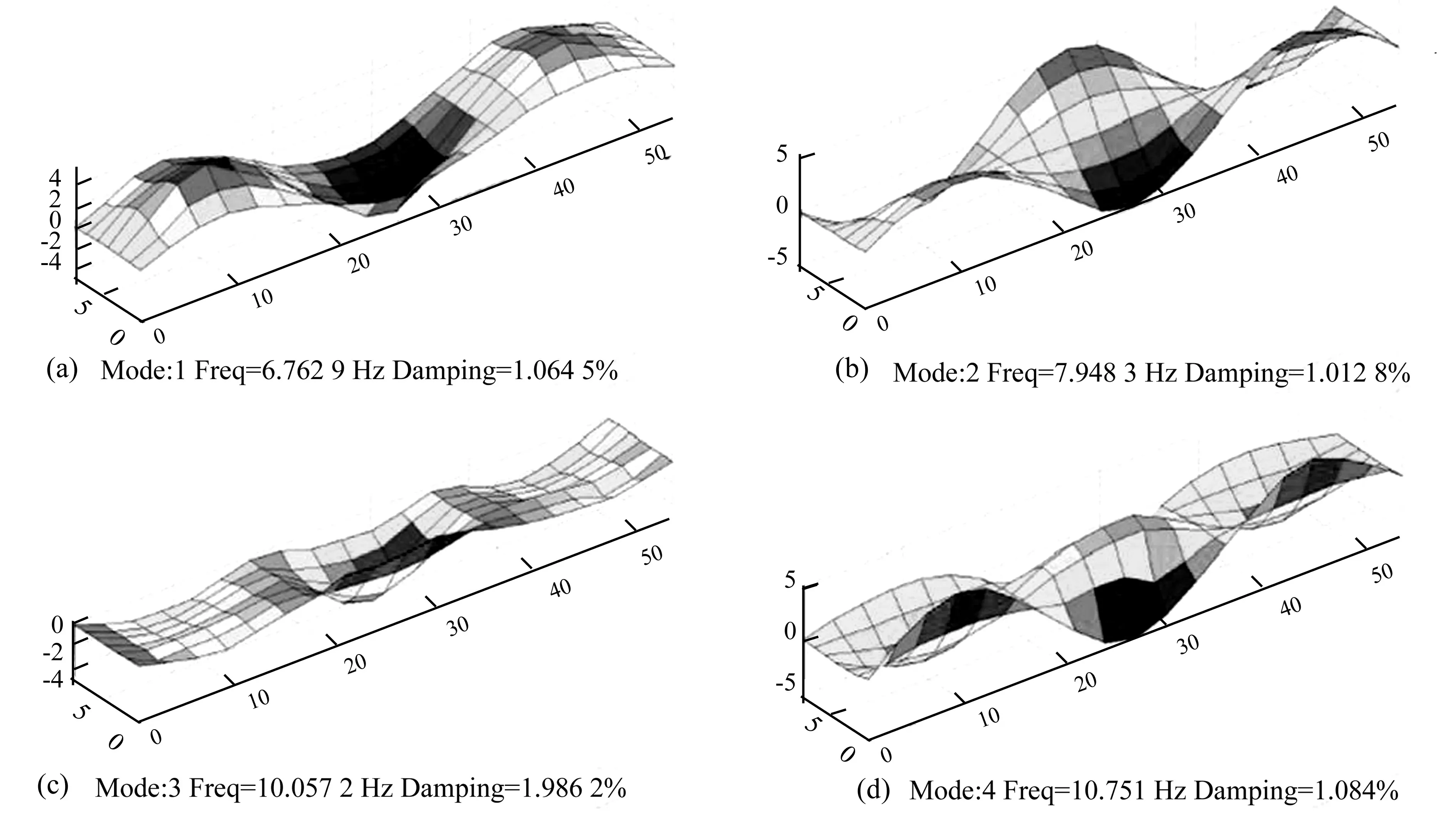
图2 Balla Balla Bridge的测量频率和振型Fig.2 Measured frequencies and mode shapes

图3 有限元模型修正过程Fig.3 The finite element model udating process

比较有限元模型修正前后结构的频率和振型，如表2所示。该基于子结构的有限元模型修正方法可以得到与整体结构非常相近的结果。修正后模型频率和实验频率之间的平均差异<1%。修正后振型的相关系数MAC从0.85提高到0.93。对于这个中型结构，在达到相同计算精度的条件下，基于子结构的有限元模型修正过程为传统方法的大约一半，极大地提高了有限元模型修正的效率。子结构方法应用于大型结构对效率的提高将更明显。

由于子结构中保留的主模态的数量会影响求解特征值和特征灵敏度的精度和效率，本文在模型修正过程中动态选取主模态。在模型修正初始阶段，选取每个子结构的前40个模态作为主模态来计算整体结构的前30个特征值和特征灵敏度。然后，随着参数逐渐接近最优解，逐步增加子结构的主模态的数量。直到在最后几步中，在每个子结构中保留90个主模态来提高特征值和特征向量计算的精度。该基于子结构的有限元模型修正过程迭代76次收敛到相同的阈值，如图3所示。基于子结构的有限元模型修正方法所花费的计算时间如表3所示，共花费48.07 h，所需时间大约是传统的整体结构模型修正方法的56%。

表1 整体结构划分为11个子结构后各子结构的信息

表2 修正前后桥的频率和振型

表3 基于整体结构有限元模型修正方法和基于子结构的有限元模型修正方法计算时间对比

5 结 论

本文提出了一种基于子结构的有限元模型修正方法。将整体结构有限元模型划分为多个独立子结构有限元模型，通过求解一个或几个发生变化的独立子结构特征解，即可求解整体结构特征解，并用于有限元模型修正和损伤识别。并且，采用子结构方法只需要计算某一个子结构特征解灵敏度矩阵即可完成对整体结构特征灵敏度的求解。当结构局部发生损伤，只需要重复某一个或几个子结构模型，避免对整体结构模型重复分析，从而有效地提高大型结构有限元模型修正的精度和效率。基于子结构的有限元模型修正方法可以有效地用于对大型结构的动力分析和健康监测中。

[ 1 ] MOTTERSHEAD J E, FRISWELL M I. Model updating in structural dynamics: a survey[J]. Journal of Sound and Vibration,1993,167(2): 347-375.

[ 2 ] 朱宏平, 黄民水. 基于环境激励的桥梁结构动力有限元模型修正研究[J]. 华中科技大学学报, 2009,26(1):1-11. ZHU Hongping, HUANG Minshui. Study on dynamic finite element model updating of bridge structures based on ambient excitation[J]. Journal of Huazhong University of Science and Technology, 2009, 26(1):1-11.

[ 3 ] 方圣恩, 基于有限元模型修正的结构损伤识别方法研究[D]. 长沙：中南大学,2010.

[ 4 ] 姜东, 费庆国, 吴邵庆. 基于摄动法的不确定性有限元模型修正方法研究[J].计算力学学报, 2014, 31(4): 431-437. JIANG Dong,FEI Qingguo, WU Shaoqing. A study on stochastic finite element model updating based on perturbation approach[J]. Chinese Journal of Computational Mechanics, 2014,31(4): 431-437.

[ 5 ] 任伟新, 陈华斌. 基于响应面的桥梁有限元模型修正[J]. 土木工程学报, 2008,41(12): 73-78. REN Weixin, CHEN Huabin. Response-surface based on finite element model updating of bridge structures[J].China Civil Engineering Journal, 2008, 41(12): 73-78.

[ 6 ] 郭勤涛, 张令弥, 费庆国. 结构动力学有限元模型修正的发展-模型确认[J].力学进展, 2006, 36(1): 36-42. GUO Qintao, ZHANG Lingmi, FEI Qingguo. From FE model updating to model validation: advances in modeling of dynamic structures[J]. Advances in Mechanics, 2006, 36(1): 36-42.

[ 7 ] BROWNJOHN J M W, MOYO P, OMENZETTER P, et al. Assessment of highway bridge upgrading by dynamic testing and finite-element model updating[J]. Journal of Bridge Engineering,2003,8(3): 162-172.

[ 8 ] JAISHI B, REN W X. Structural finite element model updating using ambient vibration test results[J]. Journal of Structural Engineering,2005, 131(4): 617-628.

[ 9 ] ZHU H P, MAO L, WENG S. A sensitivity-based structural damage identification method with unknown input excitation using transmissibility concept[J]. Journal of Sound and Vibration, 2014, 333(26): 7135-7150.

[10] WENG S, ZHU A Z, ZHU H P, et al. Dynamic condensation approach to the calculation of eigensensitivity[J]. Computers and Structures, 2014, 132(1): 55-64.

[11] WENG S, ZHU H P, XIA Y, et al. Substructuring approach to the calculation of higher-order eigensensitivity[J]. Computers and Structures, 2013, 117(2): 23-33.

[12] WENG S, ZHU H P, XIA Y, et al. Damage detection using the eigenparameter decomposition of substructural flexibility matrix[J]. Mechanical Systems and Signal Processing, 2013, 34(1/2): 19-38.

[13] WENG S, XIA Y, XU Y L, et al. Improved substructuring method for eigensolutions of large-scale structures[J]. Journal of Sound and Vibration, 2009, 323(3/4/5): 718-736.

[14] CHOI K K, KIM N H. Structural sensitivity analysis and optimization 1: linear systems[M].New York: Springer Science and Business Media, 2005.

[15] FOX R L, KAPOOR M P. Rate of change of eigenvalues and eigenvectors[J]. AIAA Journal,1968, 6(12): 2426-2429.

[16] NELSON R B. Simplified calculation of eigenvector derivatives[J].AIAA Journal,1976,24(9):823-832.

[17] CRAIG R R. Coupling of substructures for dynamic analysis:an overview[C]//Atlanta: Proceedings of 41st AIAA/ASME/ASCE/ASC Structures, Structural Dynamics, and Materials Conference, 2000:171-179.

[18] KRON G. Diakoptics[M].London:Macdonald and Co., 1963: 46-87.

Model updating based on a substructuring method

WENGShun1，ZUOYue1，ZHUHongping1,CHENBo2，ZHAOHuixian1，TIANWei1，YANYongyi1

(1. School of Civil Engineering and Mechanics,Huazhong University of Science and Technology，Wuhan 430074, China； 2. School of Civil Engineering and Architecture,Wuhan University of Technology，Wuhan 430070, China)

This paper proposes a substructure-based model updating method. The global structure was divided into independent manageable substructures, which were analyzed to calculate the substructural eigensolutions and eigensensitivity. Afterwards, the independent substructures were constrained to calculate the eigensolutions and eigensensitivity of the global structure. Finally, the eigensolutions were used for the objective function and the eigensensitivity was used to indicate the searching direction to achieve the model updating. When the local area of a structure was changed, only one or more substructures were analyzed whereas the other substructures were untouched. Since the substructures were much smaller than the global structure, the proposed method significantly improved the accuracy and efficiency of the model updating process.

model updating; substructure; damage identification; substructure; eigensolution; eigensensitivity

国家自然科学基金(51328802;51108205);中央高校基本科研业务费专项资金(2014TS130;2015MS064);武汉城建委科研项目(201511)

2015-11-23 修改稿收到日期：2016-01-31

翁顺 女，博士，副教授，1982年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.04.016