高效低噪的二维翼型优化设计

李 鑫， 屈转利， 李 耿， 刘 雨， 李国才， 余培汛

(1. 中国航天科技集团公司第四研究院第四十一所，西安 710025； 2. 西北工业大学 航空学院，西安 710072)

高效低噪的二维翼型优化设计

李 鑫1， 屈转利1， 李 耿1， 刘 雨1， 李国才1， 余培汛2

(1. 中国航天科技集团公司第四研究院第四十一所，西安 710025； 2. 西北工业大学 航空学院，西安 710072)

针对传统的气动优化设计未考虑气动噪声影响的局限性，开展了基于噪声预测模型的气动优化设计方法在二维翼型中的应用研究。建立了由几何外形参数化方法、径向基函数(Radial Basis Function,RBF)动网格技术、改进粒子群优化算法、气动分析方法、气动噪声预测方法等五大模块构成的优化设计系统，且各模块均采用标模算例进行验证。通过对二维SC(2)-0714超临界翼型进行了单点多目标优化设计。通过对比翼型几何形状、压力系数分布以及在不同迎角下的气动力系数曲线与总声压级的关系可得,翼型头部半径、厚度影响其头部压力峰值、压力恢复、逆压梯度等特性，从而影响升阻比和总声压级,逆压梯度越小，翼型的总声压级越小。优化结果表明,在设计状态下显著提高了升阻比、降低气动噪声，考虑气动噪声的二维翼型优化设计系统可在实际的工程设计中进行应用。

外形参数化；RBF动网格；改进粒子群优化算法；气动噪声；翼型；优化设计

随着航空业的发展，如何设计出更安静的飞机是目前航空界共同关注的一个焦点。欧洲的ARACE[1](Advisory Council for Aeronautics Research)组织建议民用航空工业能够在2020年前将乘客的人均噪声污染降低到现在50%。由美国NASA[2](National Aeronautics and Space Administration)牵头，FAA(Federal Aviation Administration)、飞机和发动机制造商携手合作的“安静技术验证”项目，其目的就是将飞机的可感知噪声水平在10年后降低50%，到未来25年后降低75%。由此可见，深入研究飞机噪声的成因和传播特性，进而提出改进方案以降低飞机的噪声强度，具有重要的现实意义。如何在气动外形优化设计中考虑气动噪声是一个兴起的研究热点。

另一方面，随着计算流体力学技术和优化理论的不断发展和完善，基于CFD(Computational Fluid Dynamics)技术的优化设计方法也逐渐成熟。该方法可以根据对飞行器性能的要求，直接以需要的气动力、力矩等为设计目标，以一定的流体运动方程建立目标函数与飞行器几何外形之间的关系，采用一定的优化算法，获取目标函数的最优解。气动优化设计方法最大的优点是使用灵活，受人为因素影响相对较小，适用于比较复杂的优化设计问题，在飞行器设计中广泛应用[3]。国内外主要研究工作以考虑气动力为设计目标，主要有：PALACIOS等[4]采用FFD方法对某超音速客机构型进行了气动优化设计，显著减小了激波阻力；黄江涛等[5]考虑了融合式翼梢小翼的稳健型优化设计；白俊强等[6]采用基于直接操作的FFD技术对RAE2822翼型进行了气动减阻设计。然而，耦合气动噪声、气动力的优化设计国内外研究工作比较少，主要有：POUANGUE等[7]研究了二维增升装置考虑宽频噪声的优化设计；BIZZARRINI等[8]基于NAFNOISE求解器研究了高效、低噪的二维翼型优化设计 。

本文首先阐述了自由变形参数化、RBF动网格、改进粒子群优化算法、气动力分析方法、噪声预测模型等几大部分的理论知识，并通过算例的测试对其进行了可靠性验证。基于上述几大模块，建立了一套基于噪声预测模型的翼型优化设计系统。最后，通过单点多目标约束对SC0014翼型进行优化设计，结果表明本文所采用的方法可为考虑噪声的气动优化设计提供了新的思路。

1 优化设计方法

1.1 自由变形参数化方法

自由变形技术(Free-Form Deformation，FFD)是一种气动外形参数化技术，其优点在于稳健灵活，不需要对初始外形进行拟合，可以适用于空间任意几何属性的描述，且保持外形的几何特性，如连续性、光滑性等。FFD方法是将研究对象(即待变形的翼型)嵌入FFD控制体中，通过移动各FFD控制点的位置来实现几何外形的变形，因此在应用FFD方法进行几何外形参数化的过程中，设计参数就是FFD控制点的位移。

在1986年首次提出FFD变形方法的论文中[9]，通过Bernstein基函数来定义FFD控制体包围的超曲空间几何映射关系。首先在待变形几何体周围建立FFD控制体，然后计算待变形的几何外形上每一个点在FFD 控制体中的局部坐标，局部坐标由式(1)确定

x(s,t,u)=

(1)

可以通过式(1)求出每个需要进行参数化的几何外形上每个点的局部坐标。局部坐标对于给定的FFD控制点分布只需要计算一次，而不需要在每次几何变形的过程中重复计算。在FFD控制点位置移动之后，FFD控制体中的待变形的几何外形上任一局部坐标为 (s,t,u)的点x(s,t,u)的位移Δx由式(2)确定

Δx(s,t,u)=

(2)

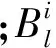
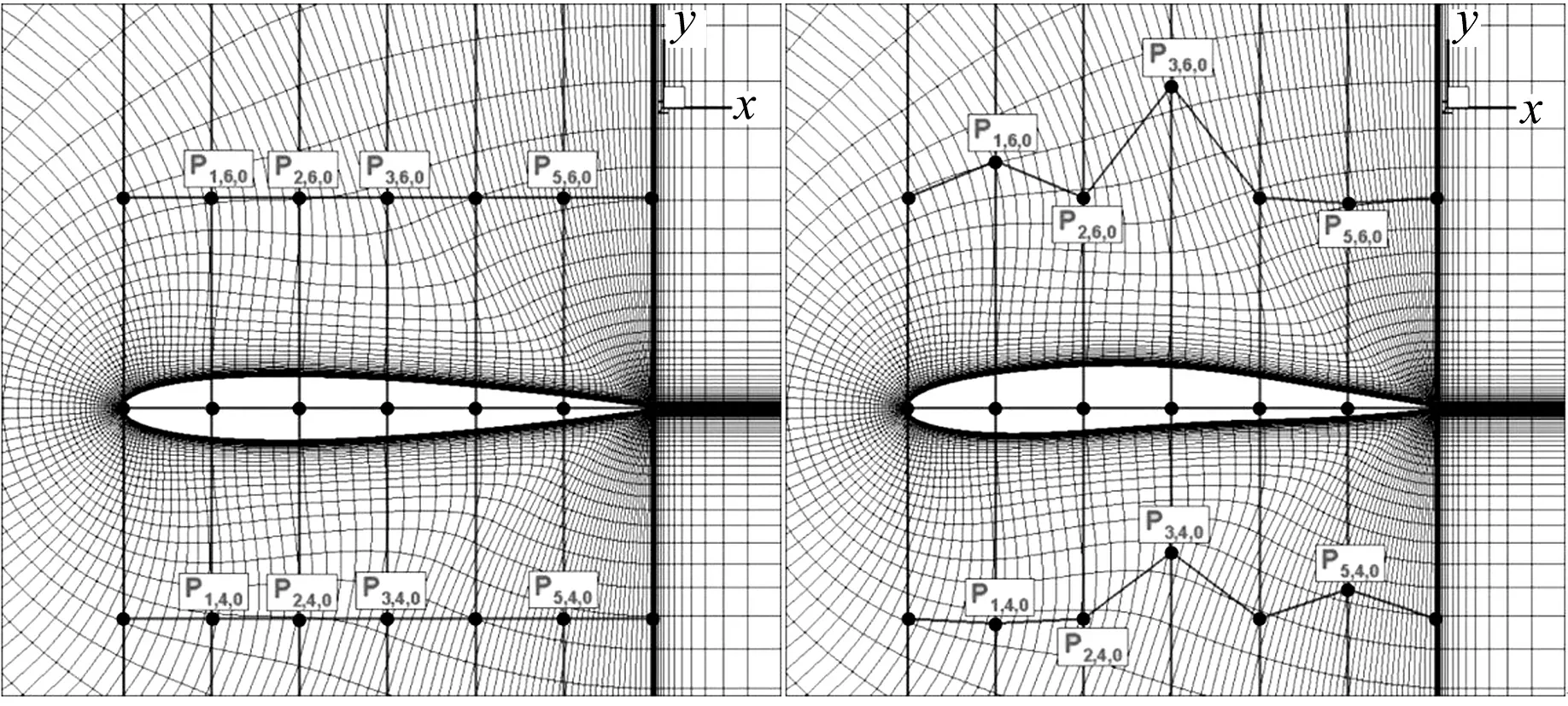
(3)

变形后几何外形上每一点的位置为

x′(s,t,u)=x(s,t,u)+Δx(s,t,u)

(4)

采用FFD方法进行翼型几何外形参数化的过程如图1所示，首先在初始翼型周围建立FFD控制点(以黑色顶点表示)，求解翼型每个几何点在FFD控制点形成的控制体中的局部坐标(s,t,u)。然后以各个FFD控制点的位移为参数，改变FFD控制点的位置，在图1中，拉动控制点使之位置发生改变。根据变形后的FFD控制点位置由式(2)计算变形后的翼型几何外形，变形后的翼型如图1(b)所示。图2为本文所建立的FFD方法在飞机其它部件中的应用。

(a) 翼型变形前 (b) 翼型变形后图1 FFD方法在翼型变形的应用Fig.1 Application of FFD method in airfoil

1.2 RBF动网格方法

在飞行器的优化设计过程中，其几何外形不断为了保证气动分析的可靠性，需使计算域中的空间网格随几何外形的变化而自动更新，这一需求孕育出了动网格技术。由于RBF动网格方法[10]除变形后网格质量高之外，还具有适应性强、执行快速等特点，本文采用RBF方法生成中间过程中的计算网格。

构建思想是在初始网格的基础上，建立边界网格与空间网格之间的插值矩阵，空间网格的变形通过边界网格的位移量来进行计算。其中边界网格与空间网格之间插值矩阵的形式如下

(5)

(6)

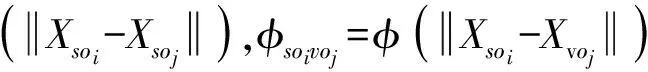
(7)

下面分别以RAE2822翼型、M6机翼的网格变形来检查程序的可靠性，具体情况分别如图2所示。由图可见，RBF动网格方法的鲁棒性高，同时网格运动前后拓扑基本保持不变，也进一步保证了优化过程中CFD计算结果的可信度。对于4万单元的计算网格，在优化之初构造表面网格和空间网格的插值矩阵耗时约1 min左右，以后每次重新建立空间网格的耗时不超过0.1 s，可见RBF动网格方法完全适用于翼型、机翼的优化设计中。

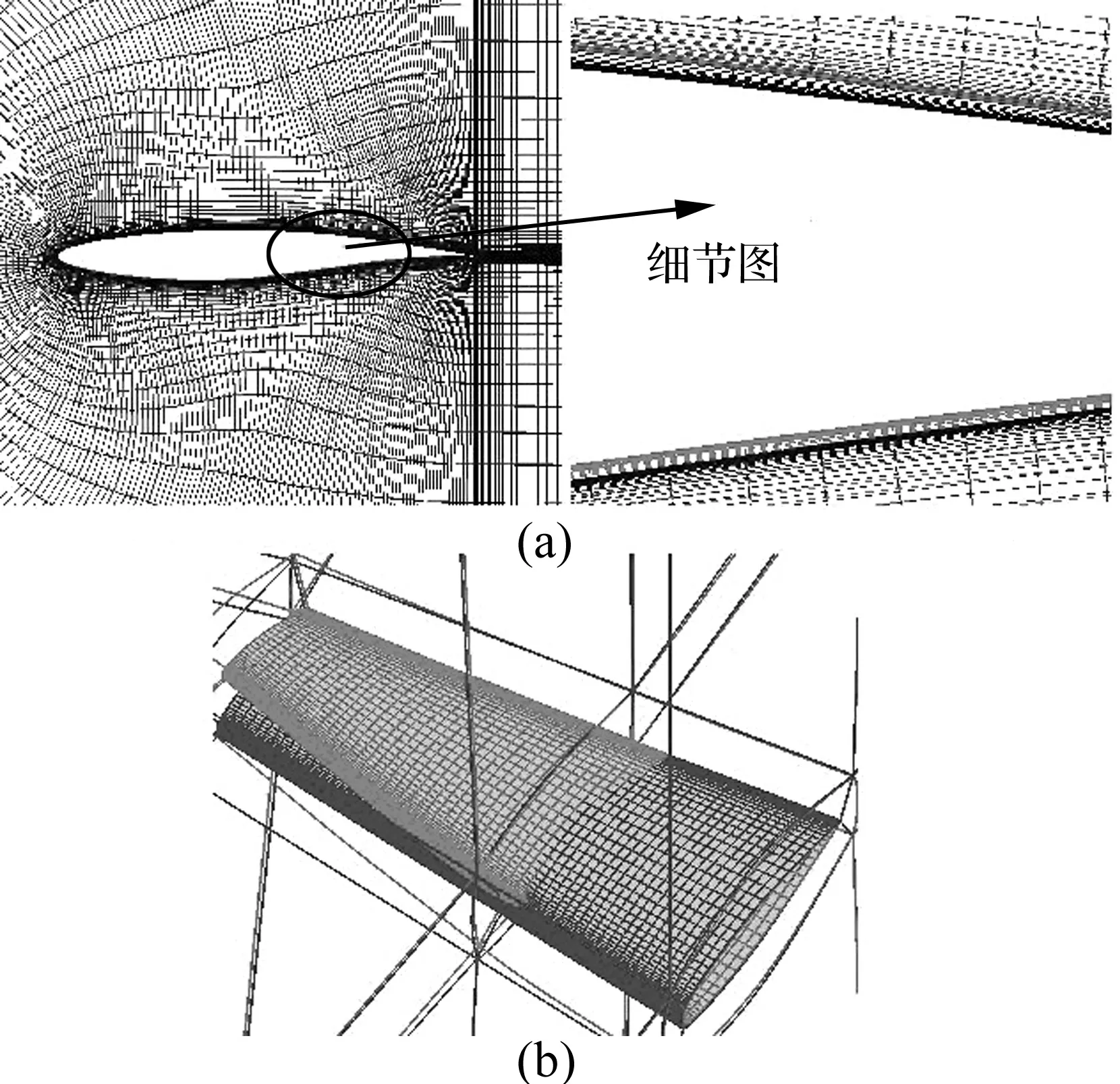
图2 二维及三维动网格示意图Fig.2 Mesh deformation of 2D and 3D

1.3 改进粒子群优化算法

优化算法的寻优能力、收敛速度都极大影响着优化设计效率。本文采用了基于二阶震荡和自然选择的改进粒子群算法(Modified Particle Swarm Optimization，MPSO)[11]，使用粒子二阶震荡来提高种群多样性，并引入自然选择思想来避免收敛速度过慢。其速度更新公式为

vi,j(t+1)=wvi,j(t)+

c1r1[pi,j-(1+ξ1)xi,j(t)+ξ1xi,j(t-1)]+

c2r2[pg,j-(1+ξ2)xi,j(t)+ξ2xi,j(t-1)]

(8)

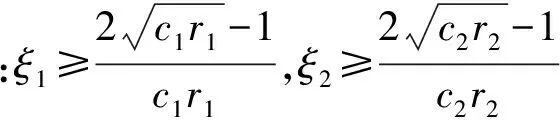
文中采用二维函数Camel函数对该优化算法的计算效率进行了测试，其中Camel函数的表达式如下，x,y的取值范围为-100～100

f(x,y)=

(9)

测试结果如表1所示，改进粒子群优化算法相对于粒子群优化算法效率更高，迭代次数更少。

表1 优化算法效率测试情况

1.4 气动噪声预测模型及验证

Ffowcs Williams和Hall的翼型/机翼噪声辐射理论已得到实验和数值模拟的证实。根据FWH方程得到机翼后缘单元声源远场辐射噪声强度的近似表达式为

(10)

式中:a∞为自由来流声速;ρ∞为来流密度;v0为特征速度尺度;f0为特征频率;L为翼型后缘距离观测点的距离。考虑后缘角β的影响的情况下，根据Howe理论[12]，噪声强度的具体表达式为

(11)

式中:β为机翼后缘角;D(θ,ψ)为指向性项，指向性项表达式为

(12)

式中:ψ为方位角;θ为极角;具体意义如图3所示。

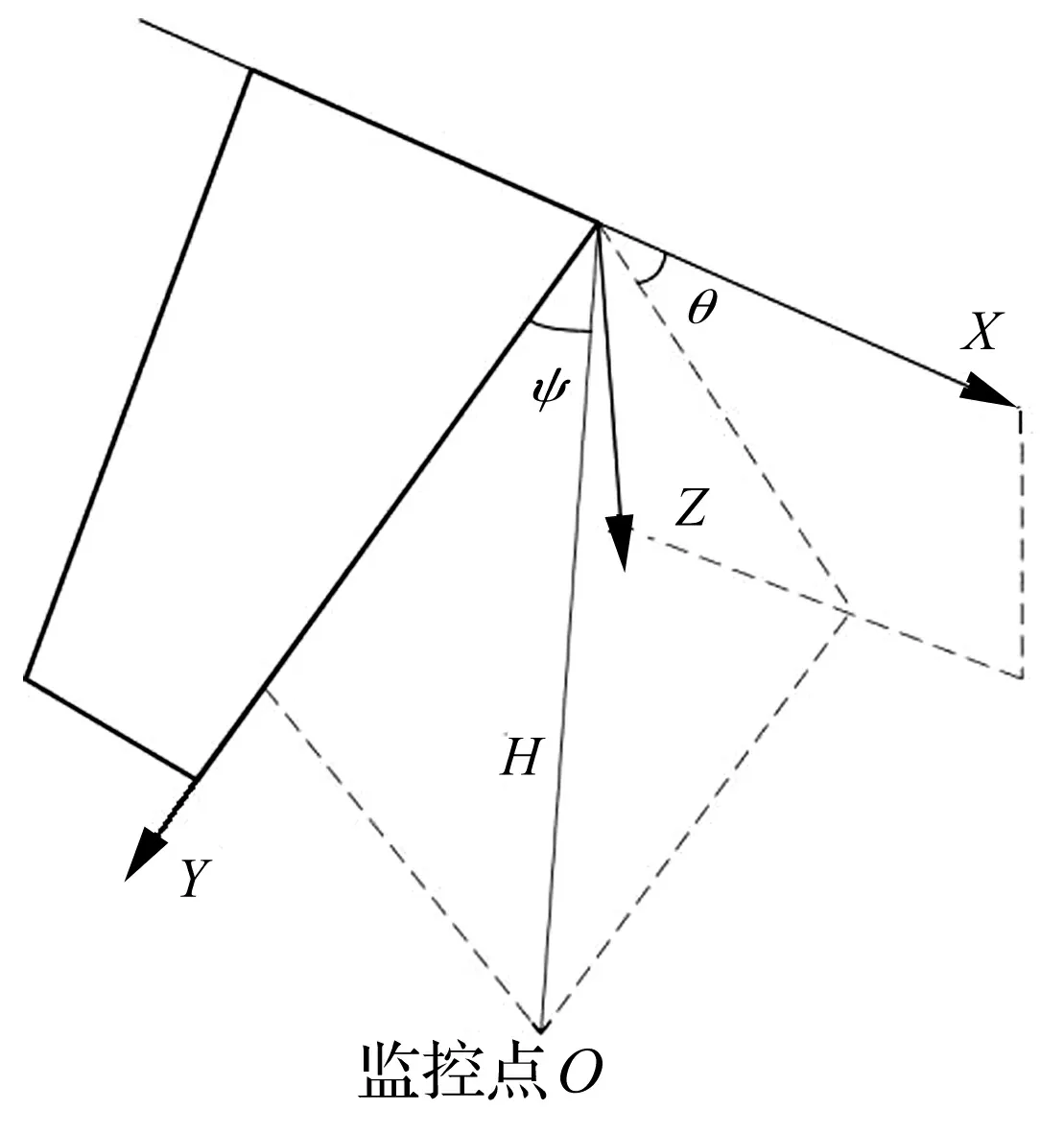
图3 指向性示意图(方位角为90°)Fig.3 Sketch of direction

考虑到湍流斯特劳哈尔关系式为

(13)

式中,l0为湍流特征尺度。将式(13)代入式(11)，则噪声强度的表达式为

(14)

式中，v0和l0分别为沿zn方向的特征速度和特征尺度，其中zn为翼型上、下翼面的后缘垂直方向zn_up和zn_down。v0和l0由式(15)所求得，其中ω为最大湍动能TKE处的湍流耗散率，TKE和ω可从求解湍流模型为k-ω或k-ε方程的雷诺平均方程获得,文中采用了湍流模型为k-ωSST方程的雷诺平均方程。

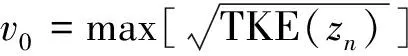
(15)

I可分为上下翼面Iup和Idown两部分噪声强度，I虽然不能准确表示噪声的强弱，但它是一个相对准确值。可通过式(16)将I转换成总声压级表达式

(16)

BROOKS等[13]通过噪声风洞实验，测量不同弦长、不同实验状态下的NACA0012翼型气动噪声，建立了一套翼型噪声数据库，并依此确立了一套半经验翼型/机翼噪声预测方法。本文选用BROOKS等用于试验分析的二维NACA0012翼型，计算状态与其试验状态相同，具体如图4所示，并将计算结果与BROOKS等通过经验公式计算的结果及ANOPP软件计算的计算结果进行对比。定义噪声监测点位于机翼后缘下方1.22 m，极角θ和方位角ψ均为90°。图5为这3种方法的结果对比图，图5中NM及OASPL的定义为

NM(i)=10(0.1(NMi-NM1))

OASPL(i)=10(0.1(OASPLi-OASPL1))

(17)

式中,NMi、OASPLi分别指的是第i个工况情况下本文所采用的噪声模型计算的结果、BROOKS等和ANOPP软件计算的结果。由图5可看出本文采用的噪声模型所计算的结果与BROOKS等及ANOPP软件计算结果相差很小，验证了本文采用的噪声预测模型具有一定的可靠性。

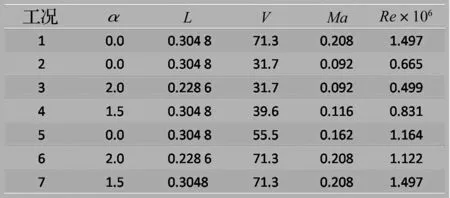
图4 计算模型计算状态图Fig.4 State of computing models

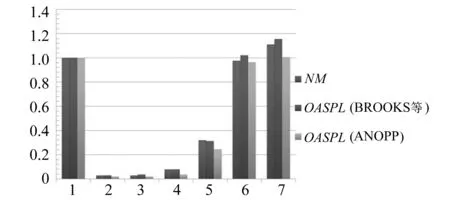
图5 计算结果对比图Fig.5 Comparison of calculation results

由声学理论可知，后缘(Trailing Edge,TE)噪声与来流速度的五次方相关，而这个影响在本文采用的噪声模型中也有所体现，因为特征速度u0将随来流速度的改变而改变。另外模型中还包括了一些显而易见的参数，例如指向性参数θ和ψ，后缘到观测点距离H，后缘角β等。除了速度和这些参数外，在翼型外形优化中该模型还考虑翼型的几何参数对噪声计算的影响，主要体现在几何参数变化带来湍动能和湍流耗散率的变化。

2 基于噪声预测模型的优化设计系统

基于第1.1节～第1.4节的理论内容，本节建立了基于噪声预测模型的优化设计系统，分别由气动外形参数化FFD模块，网格自动生成模块、气动力分析模块、气动噪声分析模块、优化搜索模块组成，其具体流程图如图6所示。

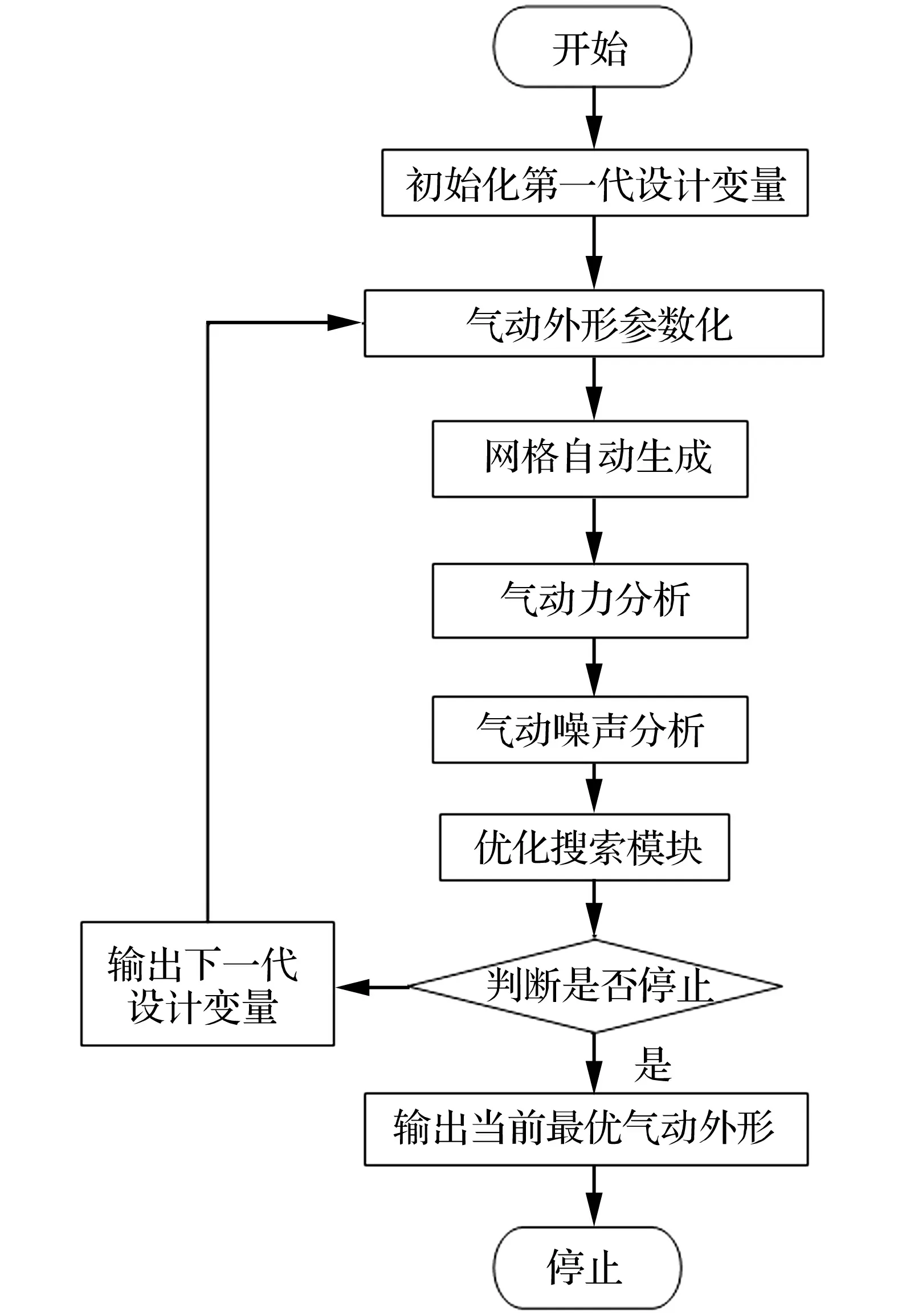
图 6 基于噪声预测模型的优化设计流程图Fig.6 Optimization flowchart with noise prediction model

3 算例分析—单点多目标优化设计

在大型客机机翼设计过程中，翼型常采用超临界翼型，为此本文选用了超临界翼型SC(2)-0714为初始翼型。其优化设计状态为：来流马赫数0.2，单位尺度雷诺数4.61×106，迎角为8°，平均气动弦长9.54 m，监测点位于后缘下方120 m处，极角和方位角为90°。优化设计目标为在起飞状态下通过优化翼型提高其升阻比，降低噪声，约束条件是翼型的最大厚度范围保证13.5%～14.5%，定攻角8°。优化设计问题可表示为

在优化设计中，设置每代种群规模100个个体，进化代数60代后结果基本收敛，Pareto前沿线如图7所示，其中纵坐标为总声压级差量(ΔNM=NMNow-NMoriginal，其中NMNow为优化历程中当前翼型所计算得到的总声压级，NMoriginal为初始翼型的总声压级)，横坐标为升阻比。

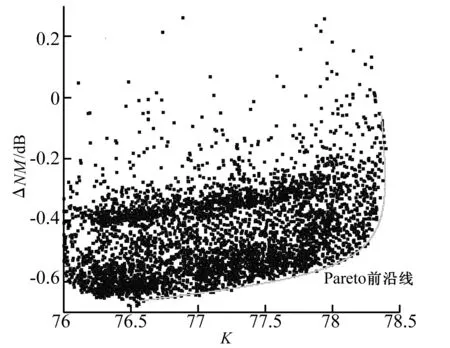
图7 Pareto前沿曲线Fig.7 Pareto frontier line

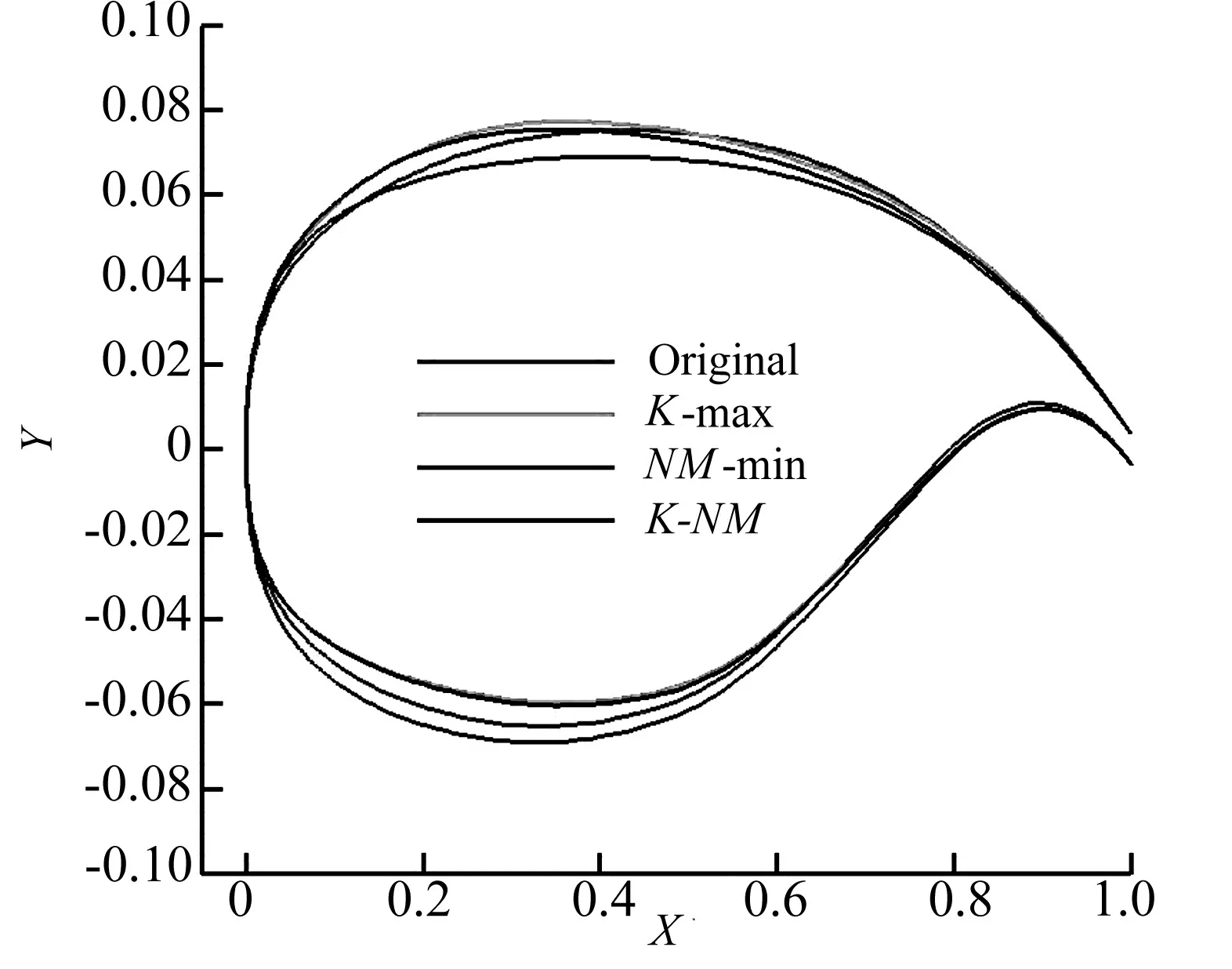
图8 优化前后的翼型几何对比Fig.8 Comparison of shape of original airfoil and optimized airfoil

优化前后的翼型几何形状、计算结果对比分别如图8和表2所示，其中Original为初始翼型，K-max为升阻比最大的翼型，NM-min为总声压级最小的翼型，K-NM为介于两优化目标间的一个翼型。对比翼型的几何外形可以看出：相对于Original翼型，K-max翼型的弯度增大、上翼面头部半径增大、下翼面头部半径减小，而NM-min翼型其趋势与K-max翼型相反。对于K-NM翼型来说，其翼型弯度、上翼面的头部半径相对于Original翼型增大，下翼面的头部半径减小，其趋势与K-max翼型相似，但其厚度比K-max翼型要小。而由表2的计算结果可以看出，优化翼型K-max比初始翼型升阻比大1.246，总声压级降低0.104 dB；优化翼型NM-min相对于初始翼型来说，升阻比降低了0.58，总声压级降低0.679 dB；优化翼型K-NM相对于初始翼型来说，升阻比增大了1.06，总声压级降低0.51 dB。

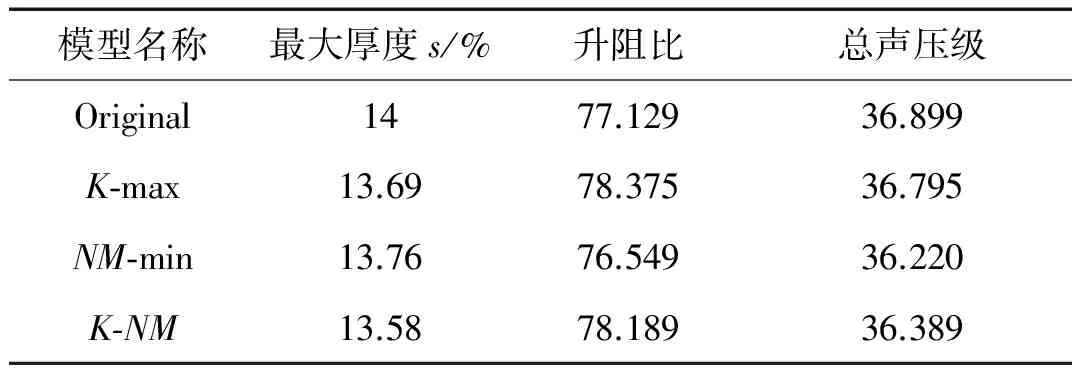
表2 优化前后的翼型计算结果对比

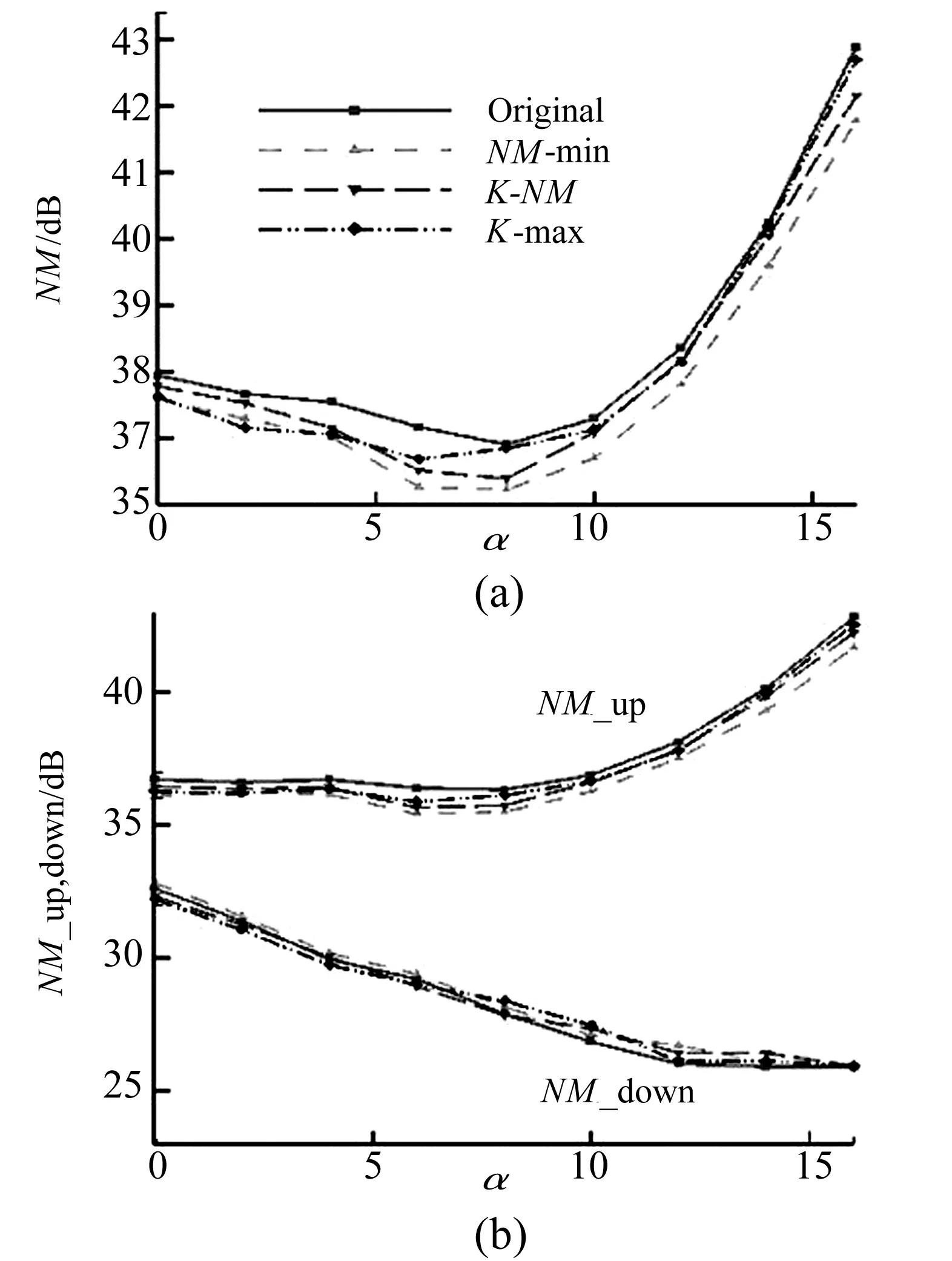
图9 声压级随攻角的变化曲线Fig.9 Curves of SPL on different α

图9为优化前后翼型在不同迎角下的总声压级、上下翼面所贡献的声压级变化曲线图，图10为优化前后翼型升力系数随迎角的变化曲线。结合图9、图10可以看出,当迎角为0°时，上翼面声源对接收点处所贡献的总声压级比下翼面要高， 主要是由于优化前后翼

型均具有一定的正弯度，虽然上下翼面均未出现分离，但由于弯度存在，上翼面的气流顺压梯度相对于上翼面更弱，气流脉动更强烈；随着迎角的增大，升力系数升高，上翼面逆压梯度增强，渐渐出现分离，导致上翼面声源强度增强，对接收点的影响越来越大；随着迎角的增大，升力系数增大，下翼面顺压梯度增强，抑制分离的出现，其声源强度出现下幅度下降，相对于上表面其对接收点总声压级的贡献变小；总声压级的变化主要来源于上翼面的声压级的贡献，随着迎角的增大，下翼面声压级的贡献比重越来越小其大小。当出现大分离(α>12°)时,上翼面声压级急速增大。

图11为优化前后翼型升阻比随升力系数的变化曲线。从图中可明显的看出：优化后的翼型K-NM和K-max最大升阻比大于初始翼型。图12为不同迎角下优化翼型K-NM与初始翼型Original的升阻比与总声压级之间的关系，黑色实线连着的两个点表示同一迎角下的计算结果，从图中可看出同一迎角下，K-NM的总声压级即小于初始翼型Original，且其升阻比也更大。通过对比分析可知该优化设计系统可进行高效低噪的二维翼型设计。

图10 升力系数随迎角的变化曲线Fig．10Liftcoefficientoverdifferentα图11 升阻比随迎角的变化曲线Fig．11Lift⁃dragratiooverdifferentα图12 不同迎角下总声压级随升阻比的变化Fig．12TotalSPLoverlift⁃dragratioondifferentα

为了进一步分析翼型的哪些因素对噪声有影响，下面将从翼型压力分布的角度分析与声压级的大小相关的因素。

文中选取了迎角8°时优化前后翼型的压力系数分布对比曲线图，具体如图13所示。对比这几组翼型可知：NM-min翼型上表面从40%位置处，其逆压梯度最小，其次是K-NM、K-max、Original，这主要和翼型的弯度有关。而在这几组翼型中，声压级的大小顺序也是如此，文中猜测声压级的大小与翼型的弯度成正比关系，其主要是由于翼型的弯度越小，压力恢复时，其出现的逆压梯度越小，以致湍流的脉动越小，从而导致声压级较小；Original的负压峰值更高，其次是NM-min、K-max、K-NM，这主要和翼型的头部半径大小相关。

4 结 论

通过采用所搭建考虑气动噪声的二维翼型优化设计系统，对比分析优化前后的翼型几何形状、压力系数分布等特点，可得出以下结论:

(1)通过采用二维翼型的优化设计系统，对超临界翼型SC(2)-0714进行考虑噪声的外形设计，验证了该系统可对比分析出不同计算状态、不同几何形状、不同迎角下的翼型总声压级。

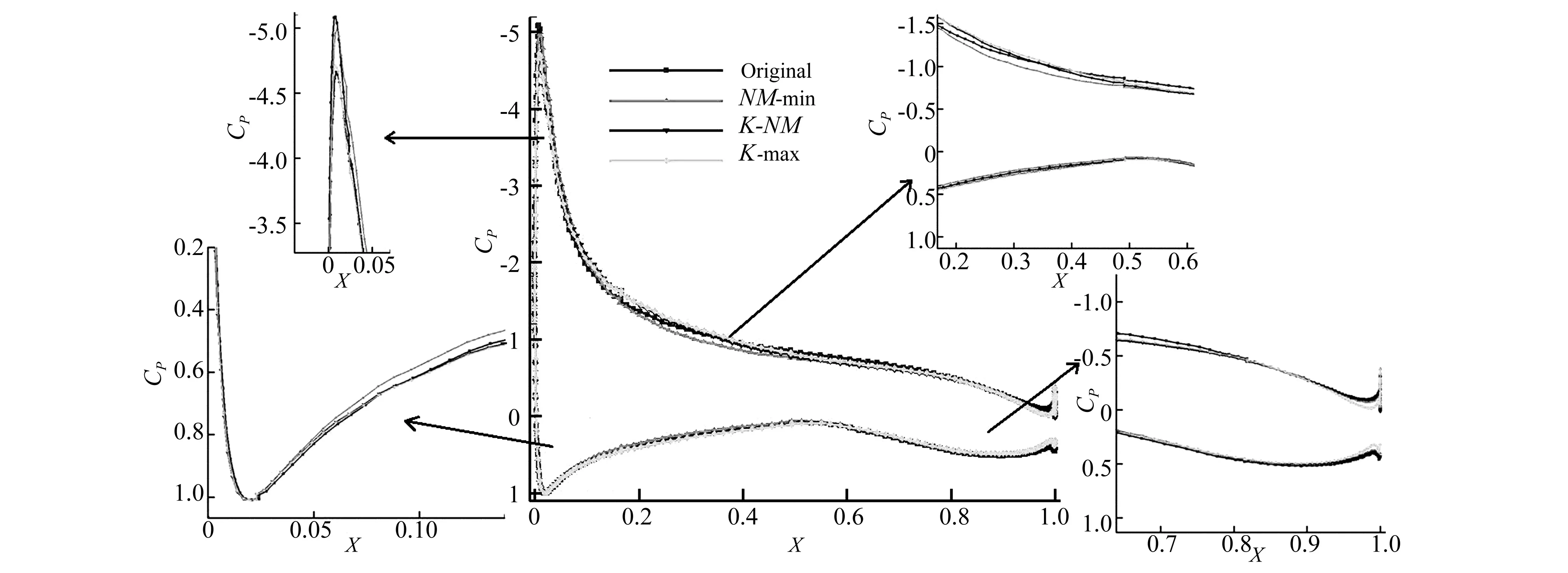
图13 翼型压力系数分布对比Fig.13 Comparison of the pressure coefficient distribution

(2)优化算例表明，应用该方法进行翼型的单点多目标优化设计，相比较于初始翼型，在不同迎角下，优化翼型K-NM在一定程度上降低气动噪声，提高升阻比。

(3)通过分析优化前后的翼型压力系数分布可知：当翼型的弯度较小时，其对应的总声压级最小，总声压级的大小与翼型的逆压梯度密切相关。

[ 1 ] HERKES B. The quiet technology demonstrator 2 flight test[C]//The Aviation Noise & Air Quality Symposium, 2006.

[ 2 ] DOBRZYNSKI W. Almost 40 years of airframe noise research-what did we achieve[J].Journal of Aircraft, 2010,47(2):353-367.

[ 3 ] 白俊强，刘南,邱亚松,等. 基于RBF动网格方法和改进粒子群优化算法的多段翼型优化[J]. 航空学报, 2013,34(12):2701-2715. BAI Junqiang, LIU Nan,QIU Yasong, et al. Optimization of multi-foil based on RBF mesh deformation method and modified particle swarm optimization algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2013,34(12):2701-2715.

[ 4 ] PALACIOS F, ALONSO J J, COLONO M. Adjoin-based method for supersonic aircraft design using equivalent area distribution[C]//San Diego:50th AIAA Aerospace Sciences Meeting and Exhibit, 2012.

[ 5 ] 黄江涛，高正红，白俊强，等. 基于任意空间属性FFD技术的融合式翼梢小翼稳健型气动优化设计[J]. 航空学报, 2013,34(1):37-45. HUANG Jiangtao, GAO Zhenghong, BAI Junqiang, et al. Study of robust winglet design based on arbitrary space shape FFD technique[J]. Acta Aeronautica et Astronautica Sinica, 2013,34(1):37-45.

[ 6 ] 白俊强，陈颂，华俊，等. 基于直接操作FFD技术的翼型气动优化设计[J]. 航空计算技术,2013,43(1):40-43. BAI Junqiang, CHEN Song, HUA Jun, et al.Application of direct manipulated FFD technique in airfoil aerodynamic optimization[J]. Aeronautical Computing Technique,2013,43(1):40-43.

[ 7 ] POUANGUE A F, MNASRI C. Parameterization and optimization of broadband noise for high-lift devices[C]//Berlin:19th AIAA/CEAS Aeroacoustics Conference,2013.

[ 8 ] BIZZARRINI N, GRASSO F, COIRO D P. Numerical optimization for high efficiency, low noise airfoils[R]. AIAA Paper, AIAA-2011-3187.

[ 9 ] SEDERBERG T W, PARRY S R. Free-form deform of solid geometric models[J]. Computer Graphics,1986,20(4):151-160.

[10] ALLEN C B, RENDALL T C S. Unified Approach to CFD-CSD interpolation and mesh using radial basis functions[R]. AIAA Paper, AIAA 2007-3804.

[11] LI L, NIU B. The particle swarm optimization algorithm[M]. Beijing: Metallurgical Industry Press, 2009:25-29.

[12] HOWE M S. A review of the theory of trailing edge noise[J]. Journal of Sound and Vibration, 1978,61(3):437-465.

[13] BROOKS T F, POPE D S, MARCOLINI M A. Airfoil self-noise and prediction[M].Washington ：NASA Reference Publication,1989.

A numerical optimization for high efficiency and low noise airfoils

LIXin1，QUZhuanli1，LIGeng1，LIUYu1，LIGuocai1，YUPeixun2

(1. The 41st Institute of the Fourth Academy of CASC, Xi’an 710025， China； 2. School of Aeronautics, Northwestern Polytechnic University, Xi’an 710072， China)

In view of the traditional aerodynamic optimization design without considering the effects of aerodynamic noise, the aerodynamic optimization design method based on noise prediction model was studied in the application of two-dimensional airfoil. The free deformation parametric method, radial basis function (RBF) mesh deformation technology, improved particle swarm optimization algorithm, pneumatic analysis method, and the aerodynamic noise prediction method for the optimization design, the five modules were established and formed a system. Finally, a single-point multi-objective optimization design of two-dimensional supercritical airfoil SC(2)-0714 was carried out. The effect of different airfoils geometry, pressure coefficient distribution, as well as the relationship between the aerodynamic coefficients and overall sound pressure level under different angles of attack were studied. The analysis showed that airfoil geometry could affect its head peak pressure, pressure recovery, adverse pressure gradient and other characteristics, which could change the lift-drag ratio and overall sound pressure level (SPL). And the adverse pressure gradient was closely related to overall SPL.Optimization results show that under the design condition the design system can significantly improve the lift-to-drag ratio, reduce the aerodynamic noise. It thus can be applied in practical engineering design.

parameterization method; radial basis function mesh deformation technology; particle swarm optimization; aeroacoustics; airfoil; optimization design

2015-11-03 修改稿收到日期：2016-01-24

李鑫 男，博士，工程师，1983年3月生

V211.3; V211.4

A

10.13465/j.cnki.jvs.2017.04.011