基于改进人工鱼群算法的输电塔塔腿拓扑优化
郭惠勇, 宋小辉, 李正良
(1. 重庆大学 土木工程学院, 重庆 400045; 2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045)
基于改进人工鱼群算法的输电塔塔腿拓扑优化
郭惠勇1, 2, 宋小辉1, 2, 李正良1, 2
(1. 重庆大学 土木工程学院, 重庆 400045; 2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045)
为了解决输电塔塔腿的优化问题,提出了基于改进人工鱼群算法的拓扑优化方法。建立了输电塔结构拓扑优化的计算模型,采用罚函数形式确定了人工鱼群算法的目标函数,并提出了拓扑变量的判定规则。采用人工鱼群算法对输电塔塔腿进行了拓扑优化研究。考虑到基本人工鱼群算法易陷入局部优化解,提出了视野和步长的变化策略,以及觅食行为的加速策略。数值算例结果表明,采用基本人工鱼群算法可以较好的优化输电塔塔腿,而在此基础上利用改进人工鱼群算法可以更有效地优化输电塔塔腿,并且其优化效率明显优化基本人工鱼群算法和差商算法。
输电塔;基结构;人工鱼群算法;塔腿;拓扑优化
近年来,特高压输电线路已经在我国得到了迅速发展。输电塔作为输电线路的重要组成部分,对其进行经济合理的设计具有重要意义[1-3]。输电塔的塔腿杆件受力非常大,且辅材众多,布置多变,在整个结构中占据了较大的造价份额。因此通过结构优化减少输电铁塔塔腿的用钢量具有现实意义。苏国柱等[4]对异型塔架结构采用了搜索准则方法进行了优化研究,主要进行了截面优化。王藏柱等[5]则采用了近似问题解的序列逐步逼近方法,研究了塔架结构的形状优化问题。王跃方等[6]则采用了刚度替代方法研究了拓扑优化问题,主要是采用了微小刚度杆件来替代删除了的杆件,但该替代方案与真实的删除方案具有差别,故只能获取近似解。李林等[7]基于压杆稳定满应力方法对塔架结构进行了离散优化研究,但该方法未考虑拓扑改变。林友新等[8]在蚁群优化思想的基础上,采用逻辑变量表示节点间是否连接,实现输电塔结构在离散系统下的拓扑优化,该方法主要是在一种基结构的子空间内寻优,容易丢失最优解。郭惠勇等[9]采用自适应遗传算法对输电塔塔身进行了拓扑优化设计,但该方法只能应用于输电塔塔身,不能应用于输电塔塔腿的拓扑优化。崔磊等[10]虽然对输电塔塔腿进行了优化研究,但是所采用的差商算法优化效率较低。故本文提出一种拓扑变量判定规则方法实现输电塔塔腿的拓扑优化,并采用了一种优化效率较高的智能化算法,即人工鱼群算法[11-13],进行输电塔塔腿的拓扑优化研究。
1 输电塔塔腿优化模型
结构优化的重要因素有设计变量、设计方案、优化算法。对于输电塔的塔腿优化问题,其设计变量应包括截面尺寸改变量和结构节点的改变量,其中对于截面尺寸改变量可根据输电塔结构的具体型钢种类不同来设立多个离散的截面尺寸设计变量。设计方案主要通过目标函数来实现,而目标函数必须是设计变量的函数。基于经济性的基本优化设计方案如下
输电塔塔腿结构在受到外部荷载作用时,通常以结构的质量为优化的基本目标函数
(1)
式中:W为结构的质量;Lj、ρj和Aj分别为第j个杆单元的长度、材料密度和截面面积;n为结构中单元的数目。其需要满足以下约束条件
(1)杆件应力约束
(2)
(2)杆件拉压长细比约束
(3)
(3)最大位移约束
ui max≤u*
(4)

2 基于改进人工鱼群算法的拓扑优化
2.1 目标函数和拓扑变量判定规则
2.1.1 拓扑优化的目标函数
人工鱼群算法(简称:鱼群算法)是模拟鱼类在自然环境中的觅食和群聚等行为而形成的一种全局优化概率搜索方法[14]。如果直接采用结构质量为目标函数,即使初始群体的位置状态都满足约束条件,经过觅食和群聚等行为后生成的新的位置状态也可能违背约束条件,这将导致基本人工鱼群算法和结构的基本目标函数难于求解这类问题。故本文采用罚函数来处理约束条件,并建立相应的目标函数。罚函数可以通过惩罚参数来避免违背约束条件的位置状态产生,从而可以顺利使用人工鱼群算法搜索到最优解。对于输电塔塔腿的拓扑优化问题,还需要考虑拓扑设计变量,则建立的拓扑优化目标函数为
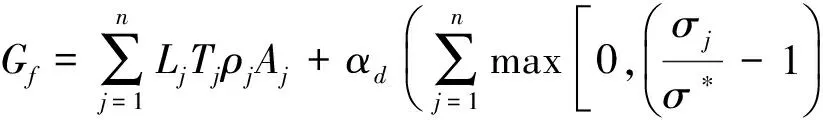
(5)
式中:Tj=0 or 1;T=[T1,T2,…,Tn]T为杆件拓扑设计变量;1表示单元保留;0表示单元不存在。由于杆件单元具有相应的节点,故节点拓扑设计变量规定为Ci,Ci=0 or 1,它由杆件拓扑设计变量决定,1表示节点保留,0表示节点不存在。αd为惩罚因子,对于最小优化问题,需要选取一个较大的数,本文取1010,s为自由度数。
2.1.2 拓扑变量判定规则
对基结构进行杆件删减是一种有效的拓扑优化方法,杆件单元是否删除取决于单元截面的利用率,若寻优的过程中,单元承受的截面应力小于设定的限值,该单元的拓扑变量Tj为0。杆件单元拓扑变量和节点拓扑变量密切相关,而一个节点往往与多个单元相连,单元的删除并不意味着相应节点的删除,需要一定的判定准则。故本文建立的拓扑变量判定规则如下:
(1)对于不承受荷载的可删除节点且不是支座节点,如果仅有2个单元与之相连,应删除该节点,该节点拓扑变量Ci为0。
(2)对于承受荷载的节点,应保证至少2个单元与之相连,只有2个单元时还需保证不在同一条直线上。
(3)对其他不可删除节点,应保证至少有3个单元与之相连。
(4)删除一个节点,与之相连的所有单元的拓扑变量都变为0,若导致该删除节点周边的节点因连接单元数量不足出现机构,算法程序会自动识别并产生备用单元,避免机构发生。
2.2 基本人工鱼群算法
人工鱼群算法主要模仿鱼类的觅食、聚群、追尾等行为,通过人工鱼在虚拟水域中的游动进行优化。人工鱼群算法的基本操作如下所示。
2.2.1 觅食
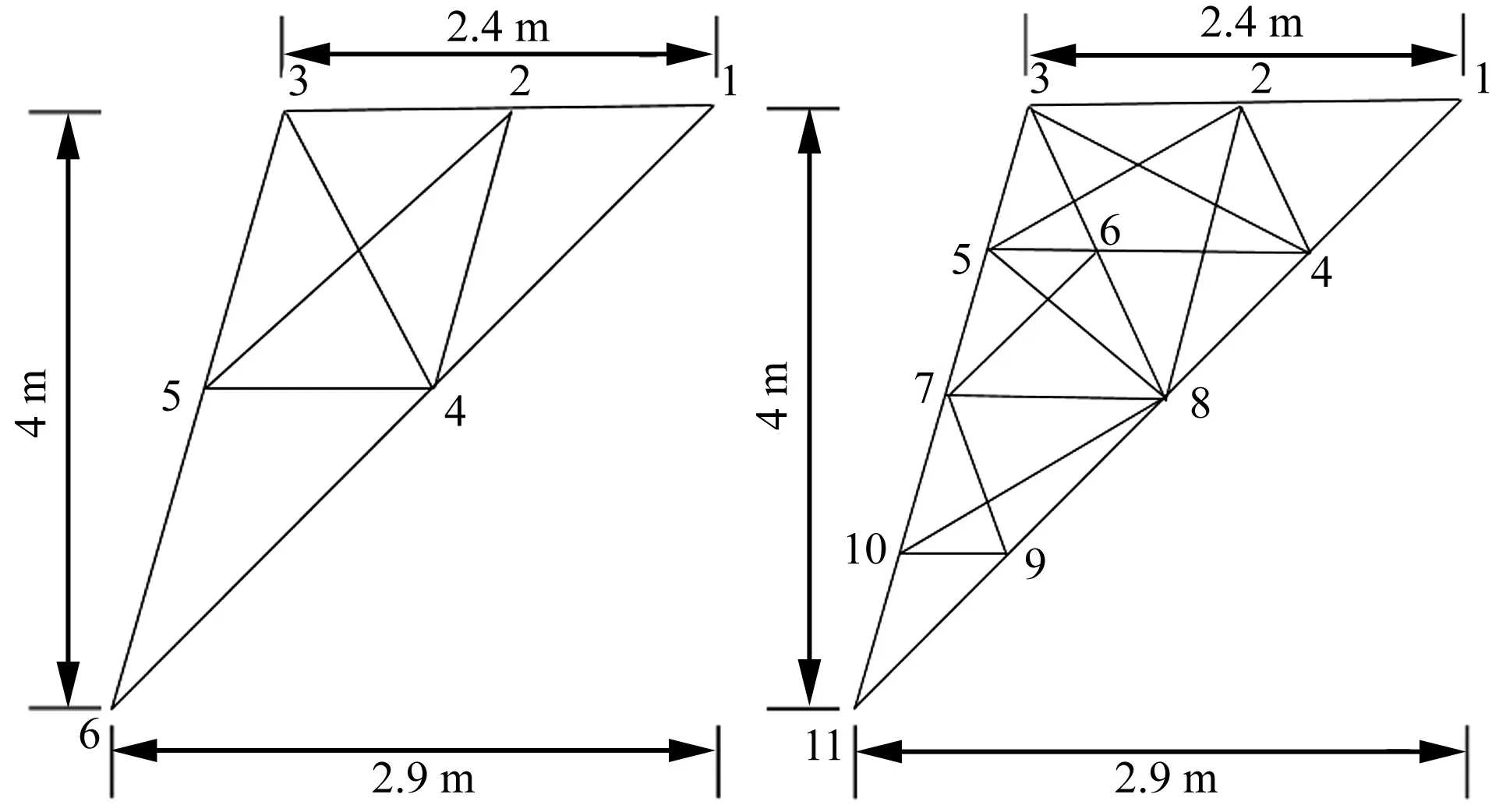
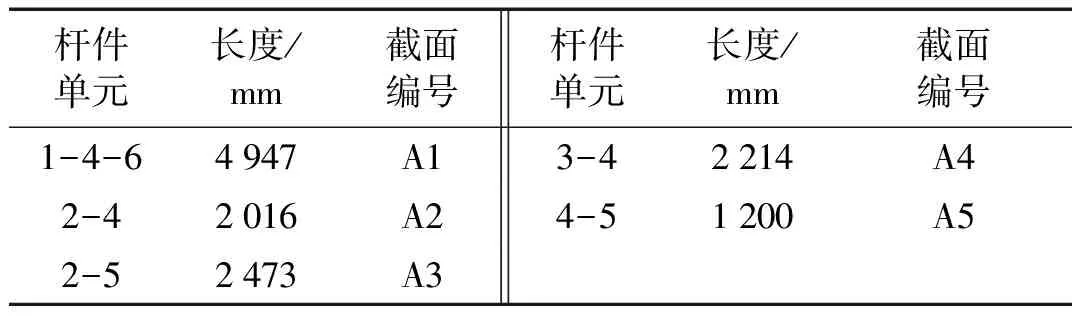
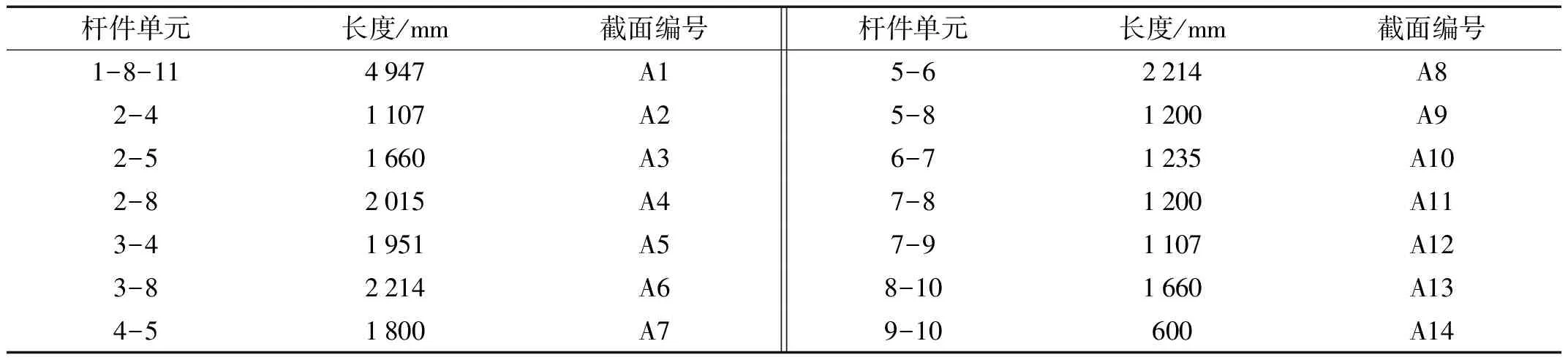
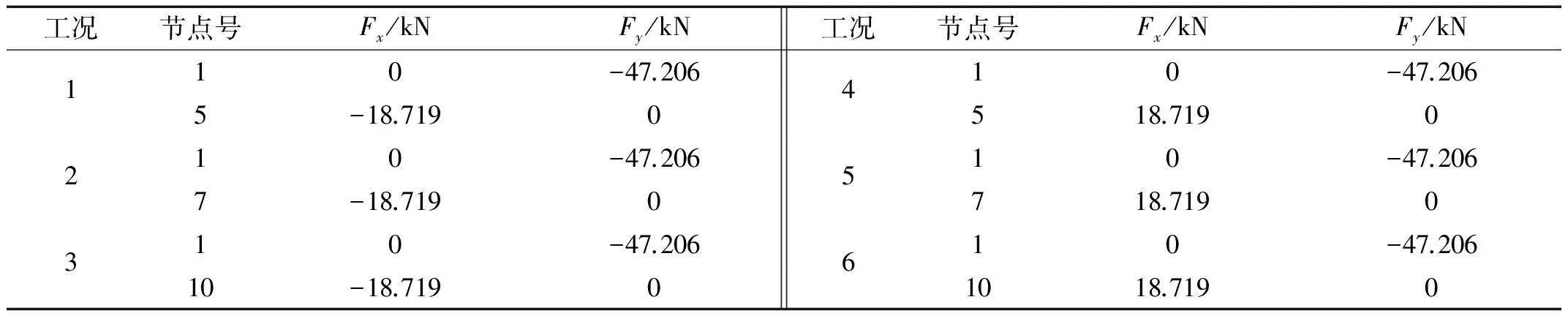
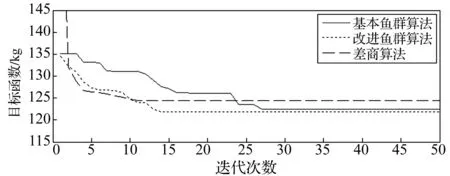
设人工鱼当前状态为Xi,在其感知范围内随机选择一个状态Xj,如果在求极小值问题中(本文的目标函数为极小值问题),目标函数值Yj (6) 如不满足,则重新随机选择状态Xj,再次判断是否满足前进条件;反复Try_number次后,如果仍不能满足前进条件,则随机移动一步。 2.2.2 群聚 设人工鱼当前状态Xi,探索当前邻域内(即dij (7) 否则执行觅食行为。 2.2.3 追尾 设人工鱼当前状态Xi,探索当前邻域内的伙伴中目标函数为最小的伙伴Xmin,并且Xmin邻域内的伙伴数目nf满足Yminnf (8) 否则执行觅食行为。 2.2.4 随机行为 人工鱼在视野范围内随机选择一个状态,然后向该方向移动,可以避免陷入局部优化解 Xnext=Xi+Visual×step×rand() (9) 随机行为与觅食行为密切相关,是对觅食行为的一个补充。 2.3 改进的人工鱼群算法 2.3.1 视野和步长的改进 视野和步长在寻优过程中是非常重要的。当视野和步长固定不变时,将导致算法后期收敛速度慢,容易陷入局部最优解。故本文将动态调整人工鱼的视野和步长,在算法运行前期,为了增强算法的全局搜索能力和收敛速度,采用较大的视野和较大的步长,使人工鱼在更大的范围内进行搜索,随着搜索的进行,视野Visual和移动步长step逐步减小,在算法后期,算法逐步演化为局部搜索,主要在最优解附近区域进行精细搜索,从而提高算法的局部稳定能力和最优结果的精度。 (10) (11) 式中:Visual0为搜索视野初值;step0为移动步长初值;tp为当前所有杆件拓扑变量之和;t为当前迭代次数;m为初始结构杆件单元数量;T为最大迭代次数;p、q、α为删除杆件单元对视野和步长的影响系数,取值范围为[0,1]。 2.3.2 觅食行为改进 在觅食行为中,人工鱼随机选择一个状态Xj,如果该状态优于当前位置Xi,则直接移动到该位置,否则尝试二次搜索,直到搜索到优于当前位置的状态,最多尝试Try-number次。为了加快觅食行为寻优速度,本文引入一种加速单元截面优化机制。由于各杆件单元所受的荷载不一定,应力也有大有小,若某些单元的的应力σ超过应力允许限值σ*,说明必须要增大其截面积以增强该单元承载能力,算法程序会自动记录该单元截面积需要加强,则在下次迭代循环前会自动选择临近大一型号的截面;相反若当前单元的截面应力过小,说明必须要减小其截面积以增加材料的利用率,算法程序自动记录该杆单元利用率不足,在下次迭代循环前自动替换邻近小一型号的截面,从而使单元迅速达到满应力设计状态,加快寻优速度。 (12) (13) 2.4 优化过程 拓扑优化具体过程如图1所示。 图1 拓扑优化设计流程Fig.1 Flow chart of topology optimization 一输电塔塔腿的基结构模型如图2所示,前期已经计算得到了塔腿斜材和主材的内力,主材与横隔材均以选定不参与杆件拓扑与截面优化。主材采用3分分格,对斜材和辅材进行截面和拓扑优化,允许9个节 点任意相连,塔腿可以组合成任意拓扑形式。杆件界面库共有13种类型:A={L40×3(2.360 cm2),L45×3(2.660 cm2),L40×4(3.090 cm2),L45×4(3.490 cm2),L50×4(3.900 cm2),L45×5(4.290 cm2),L56×4(4.390 cm2),L50×5(4.800 cm2),L63×4(4.980 cm2),L56×5(5.420 cm2),L63×5(6.140 cm2),L70×5(6.880 cm2),L75×5(7.410 cm2)}。塔腿基结构模型单元序号及截面编号见表1。根据塔体内力,使用截面法计算节点1上z方向荷载,并按架空送电线路杆塔结构设计技术规程规定[15],杆塔辅材在其支撑点所提供的支撑力一般不低于所支撑主材内力的2%、斜材内力的5%,算得6、8节点的荷载值,该塔腿基结构模型的四种荷载工况如表2所示。塔腿辅材的许用应力为205 MPa,压缩许用细长比为200、拉伸许用长细比400,位移控制点为1点,位移允许值为0.02 m,人工鱼群算法控制参数为:人工鱼为20条,最大迭代次数50次,Try-number是15,拥挤度因子为0.28,视距为4,步长为1.5。 图2 塔腿原始基结构模型Fig.2 Basic structure of tower leg 杆件单元长度/mm截面编号杆件单元长度/mm截面编号1-4-7-94947A15-6400A62-41353A23-72706A72-61912A35-81450A83-41955A46-71475A94-61600A57-8800A10 表2 塔腿基结构模型的荷载工况 该输电塔腿基结构的拓扑优化结果见表3,塔腿基结构的拓扑优化设计结果见图3,拓扑优化收敛曲线见图4。由表3可知,对比基本鱼群算法、改进的鱼群算法、差商算法等三种优化算法,拓扑形式一致,但运用改进的鱼群算法的优化质量结果更好,比基本鱼群算法减小了约8.4%,比差商算法减小了约8.1%;收敛速度也得到较大幅度提高,均超过其他两种算法。改进鱼群算法优化的最终结构参数见表4,表中的最大等效应力考虑了杆件的稳定系数,稳定系数主要是利用架空送电线路杆塔结构设计技术规程附录C的稳定系 数公式进行计算。另外,控制点为1点,其计算位移为0.000 5 m,远低于允许值。 图3 塔腿基结构的优化模型Fig.3 Optimized structure of tower leg 优化算法截面编号A1A2A3A4A5A6A7A8A9A10结构质量/kg基本鱼群算法110011100011123.343改进的鱼群算法11002100011113.008差商算法11005500041122.988 表4 优化结构的一些参数 图4 输电塔塔腿拓扑优化收敛曲线Fig.4 Topology optimization convergence curve of transmission tower leg 由于该塔腿主材采用固定三分格式,基于该基结构模型的拓扑优化的优化结果形式只能是三分格结构,可能不是全局最优解,原因是基结构法确定初始结构时可能已经将全局最优解排除在外。只有摆脱单一的基结构,在尽量多的结构形式中进行研究,才易找到最优解正。为了减小对单一形式的基结构拓扑优化带来的不利影响,本文又引入两种塔腿基结构模型来丰富求全局最优解的解空间,以使搜索到的最优解更具全局性。塔腿基结构模型a和塔腿基结构模型b分别见图5、图6。 塔腿基结构模型a和塔腿基结构模型b的杆件单元序号及截面编号分别见表5、表6。 图5 塔腿基结构模型aFig.5Basicstructureaoftowerleg图6 塔腿基结构模型bFig.6Basicstructureboftowerleg 表5 塔腿基结构模型a杆件序号及截面编号 按照架空送电线路杆塔结构设计技术规定,杆塔辅材在其支撑点所提供的支撑力一般不低于所支撑主材内力的2%、斜材内力的5%,算得塔腿基结构模型a和塔腿基结构模型b的荷载工况,分别见表7、表8。 该输电塔腿基结构模型a和输电塔腿基结构模型b拓扑优化结果分别见表9、表10。 表6 塔腿基结构模型b杆件序号及截面编号 表7 塔腿基结构模型a的荷载工况 表8 塔腿基结构模型b的荷载工况 表9 塔腿基结构模型a拓扑优化结果 表10 塔腿基结构模型b拓扑优化结果 该输电塔腿基结构模型a和输电塔腿基结构模型b的拓扑优化设计结果分别见图7、图8。由图7、图8可知,三种算法分别基于结构模型a和结构模型b的优化结果设计形式是一致的,但是与基于单一基结构的优化结果相比,拓扑形式有很大改变。另外,模型a基结构为二分格形式,模型b基结构为四分格形式,根据技术规定的要求,两者的载荷工况不同,故优化结果不同。 图7 塔腿构型a的优化模型Fig.7Optimizedstructureoftowerlega 图8 塔腿构型b的优化模型Fig.8 Optimizedstructureoftowerlegb 图9、图10为本文采用的拓扑优化方法与差商法对该输电铁塔塔腿构型a和构型b的拓扑优化收敛曲线。塔腿构型a单元数目比较少,基本鱼群算法与改进的鱼群算法优化结果一样,但是寻优效果好于差商算法,比差商算法减少2.3%。塔腿构型b的优化结果显示改进的鱼群算法比基本鱼群算法减少0.5%,比差商算法减少2.0%。改进的鱼群算法的收敛速度均优于基本鱼群算法和差商算法。比较三种基结构模型的拓扑优化结果,三分格是该输电塔塔腿最优的布置形式。 图9 塔腿构型a的拓扑优化收敛曲线Fig.9 Topology optimization convergence curve of tower leg a 图10 塔腿构型b的拓扑优化收敛曲线Fig.10 Topology optimization convergence curve of tower leg b 本文提出了基于改进人工鱼群算法的输电塔塔腿拓扑优化方法。该方法首先建立了基于罚函数和拓扑变量的目标函数,提出了拓扑变量判定规则,然后利用人工鱼群算法进行输电塔塔腿的拓扑优化研究,并考虑到基本人工鱼群算法易陷入局部优化解问题,提出了视野和步长的变化策略,以及觅食行为的加速策略。通过数值计算和理论分析,可以得出以下结论: (1)改进的人工鱼群算法有效的提高了运行速度以及在解空间中的搜索能力和收敛精度,其搜索效率明显好于基本人工鱼群算法和差商算法。 (2)提出的拓扑变量判定规则主要适用于输电塔塔腿结构。 (3)通过引入多种基结构模型,可以丰富搜索的解空间域,能够有效避免陷入局部优化解,使得结构拓扑优化结果更加接近于最优解。 [ 1 ] 李宏男,白海峰.高压输电塔-线体系抗灾研究的现状与发展趋势[J].土木工程学报,2007,40(2):39-46. LI Hongnan, BAI Haifeng. State-of-the-art review on studys of disaster resistance of high-voltage transmission tower-line system[J].China Civil Engineering Journal,2007,40(2):39-46. [ 2 ] 田利,马瑞升,朱峰. 高压输电塔-线体系抗震的研究进展[J].世界地震工程,2014,30(1):87-92. TIAN Li, MA Ruisheng, ZHU Feng. Seismic research progress of high voltage transmission tower-line system[J]. World Earthquake Engineering, 2014,30(1):87-92. [ 3 ] YANG Fengli, YANG Jingbo, NIU Huawei. Design wind loads for tubular-angle steel cross-arms of transmission towers under skewed wind loading[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 140(5):10-18. [ 4 ] 苏国柱,王永焕,徐海翔,等. 异型高耸塔架结构优化设计[J]. 工业建筑,2005,35(2): 57-59. SU Guozhu, WANG Yonghuan, XU Haixiang, et al. Structural optimum design of allotype high tower[J]. Industrial Construction, 2005, 35(2): 57-59. [ 5 ] 王藏柱,董桂西. 架空输电铁塔形状优化的研究[J]. 华北电力大学学报, 2001, 28(2): 100-104. WANG Cangzhu, DONG Guixi. Investigation on shape optimization of transmission tower[J]. Journal of North China Electric Power University, 2001, 28(2): 100-104. [ 6 ] 王跃方,孙焕纯.多工况多约束下离散变量桁架结构的拓扑优化设计[J].力学学报,1995,27(3):365-369. WANG Yuefang, SUN Huanchun. Optimal topology designs of trusses with discrete size variables subjected to multiple constraints and loading cases[J]. ACTA Mechanica Sinaca, 1995,27(3):365-369. [ 7 ] 李林,宋梦娇,王达达,等.输电塔架设计中的离散优化方法研究[J].华北电力大学学报,2012,39(6):35-39. LI Lin, SONG Mengjiao, WANG Dada, et al. Study of discrete optimum method in transmission tower design[J]. Journal of North China Electric Power University, 2012,39(6):35-39. [ 8 ] 林友新,张卓群,李宏男,等.输电塔结构的拓扑优化设计方法[J].沈阳建筑大学学报,2013,29(4):655-661. LIN Youxin, ZHANG Zhuoqun, LI Hongnan, et al. Topology optimization design of transmission tower structure[J]. Journal of Shenyang Jianzhu University, 2013,29(4):655-661. [ 9 ] 郭惠勇, 李正良, 罗乐. 基于离散变量的大跨越输电塔架构不同优化方法研究[J].工程力学,2009,26(12):181-188. GUO Huiyong, LI Zhengliang, LUO Le. A study of different optimization methods of long-span transmission tower based on discrete variables[J].Engineering Mechanics, 2009,26(12):181-188. [10] 崔磊,邓洪洲.基于差商算法的输电铁塔塔腿辅材的拓扑优化[J].特种结构,2007,24(3):89-92. CUI Lei, DENG Hongzhou. Topology optimization for the redundant members of transmission tower’s legs based on relative difference quotient algorithm[J]. Special Structures, 2007, 24(3):89-92. [11] XIAO J M,ZHENG X M,WANG X H,et al.A modified artificial fish-swarm algorithm [C]//Proceedings of the World Congress on Intelligent Control and Automation(WCICA).Washington:IEEE,Computer Society,2006:3456-3460. [12] WANG L G,HONG Y.A multiagent artificial fish-swarm algorithm[C]//The 7th World Congress on Intelligent Control and Automation.Washington:IEEE,Computer Society,2008:3161-3166. [13] GELENBE E,SCHMAJUK N,STADDON J,et al.Autonomous search by robots and animals:a survey[J]. Robotics and Autonomous Systems,1997,22:23-34. [14] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38. LI Xiaolei, SHAO Zhijiang, QIAN Jixin. An optimizing method based on autonomous animats: fish-swarm algorithm[J]. Systems Engineering—Theory & Practice, 2002,22(11):32-38. [15] 西南电力设计院.架空送电线路杆塔结构设计技术规定:DL/T 5154—2012[S].北京:中国计划出版社,2002. Topology optimization of transmission tower legs based on an improved artificial fish-swarm algorithm GUOHuiyong1, 2,SONGXiaohui1, 2,LIZhengliang1, 2 (1. School of Civil Engineering, Chongqing University, Chongqing 400045, China; 2. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing University,Chongqing 400045, China) In order to solve the structural optimization problem of transmission tower legs, a topology optimization method based on artificial fish-swarm algorithm (AFSA) was presented. First the calculation model of the topology optimization of transmission tower legs was established. Topology variable optimization rules were proposed. Then, an artificial fish-swarm algorithm was utilized to optimize the transmission tower legs. Considering the optimization results of simple AFSA were not very good, two kinds of improved strategies: position formula with dynamic visual and step, acceleration strategy, were presented. Simulation results show that the simple AFSA and the improved AFSA can optimize the transmission tower legs. The optimization results of the improved AFSA method are obviously better than those of the simple AFSA and the difference quotient algorithm. transmission tower; basic structure; artificial fish-swarm algorithm; tower legs; topology optimization 国家自然科学基金资助项目(51468058);国家自然科学基金资助项目(51578094);重庆市建设科技计划项目(2014-0005) 2015-08-07 修改稿收到日期:2016-01-21 郭惠勇 男,博士,副教授,1971年生 TB123 A 10.13465/j.cnki.jvs.2017.04.009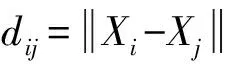


3 优化计算














4 结 论

