基于系统约束的重型汽车动力学建模及分析

黄 康 段松林 甄圣超 徐 锐 薛永昌

1.合肥工业大学机械与汽车工程学院，合肥，2300092.福马汽车零部件有限公司，马鞍山，243100

基于系统约束的重型汽车动力学建模及分析

黄 康1段松林1甄圣超1徐 锐1薛永昌2

1.合肥工业大学机械与汽车工程学院，合肥，2300092.福马汽车零部件有限公司，马鞍山，243100

针对传统方法建立汽车整车动力学模型中存在的过程复杂、约束难以确定等问题，以重型汽车整车为对象，应用Udwadia-Kalaba理论提出了一种基于系统约束的离散化模型，并进行了动力学分析。该模型考虑了汽车在正常行驶过程中路面对4个轮胎的真实激励情况，重点研究了整车z向的动态特性。通过MATLAB仿真得到空载和D级路面激励情况下的振动特性，并将该模型与传统方法建立的模型进行比较，验证了模型的正确性，同时分析了车身关键位置及驾驶员位置动态特性曲线。

重型汽车；系统约束；离散化动力学系统；Udwadia-Kalaba理论；动力学分析

0 引言

Udwadia-Kalaba方法是在现今非常完善的机械原理基本方法上进一步引申出来的理论方法[1-5]，是一种描述含约束的多体动力学系统的基本方法。该方法基于高斯原理，通过广义逆运算，将约束转化为约束力,与拉格朗日方法相比，避免了在求约束力过程中获取拉格朗日乘子这一繁琐过程。与Gibbs、Appell等原理相比，Udwadia-Kalaba方法可用于非理想约束的情况，即当系统不满足达朗贝尔原理时，Udwadia-Kalaba方程也是适用的(但需要通过实验测定相关数据)。这是Udwadia-Kalaba方法相较于其他方法的主要优势。从Udwadia-Kalaba方法提出至今，已经有许多学者针对此方法做了大量的研究。CHEN[6]在Udwadia-Kalaba方程的基础上提出了伺服约束控制，并将其运用到工程实际中，认为只要设计合理，就可以满足控制要求。文献[7-8]将Udwadia-Kalaba方程运用到多体动力学系统仿真和天体运动研究中，证实了其正确性与实用性。

汽车整车动力学模型的建立是平顺性和操纵稳定性等研究的重要内容，现今针对汽车整车建模的方法有很多，围绕不同的建模方法也有不少研究成果。在传统方法中，文献[9-10]运用牛顿动力学方法建立了多自由度整车动力学方程，并验证了其正确性，但建模过程复杂。张云清等[11]用拉格朗日方法得到的整车模型，在实际工程应用中有很高的应用价值，但在实际时，拉格朗日乘子不易确定。常规方法建模过程中需要考虑所有自由度之间的关系，步骤较为繁琐，对于简单模型比较方便，但对于多自由度的复杂模型计算量极大，通常需要简化处理，影响了模型的准确性。除了传统方法外，李杰等[12]将有限元的思想运用到汽车动力学模型的建立中，将振动结构离散化，采用节点位移法得到系统模型，是一种比较新颖的方法。工程中运用较多的是ADAMS等多体动力学软件，这些软件是基于参数化数学模型建立虚拟样机仿真的，计算前期需要进行大量的建模工作，计算结果的正确性高度依赖模型的准确性，对使用者有较高的经验要求。本文将车身及车桥整体结构离散化，采用Udwadia-Kalaba方法建立汽车多体动力学模型。

1 含约束运动系统的一般动力学方程

在Udwadia-Kalaba理论中，需要建立系统在无约束条件下n个自由度的动力学方程，这里用q=[q1q2…qn]T表示系统的n维广义坐标，可通过牛顿力学方法或拉格朗日方法得到如下方程：

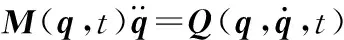
(1)

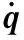
(2)

下面考虑约束对系统的影响。假设系统内施加有m个约束，则约束方程为

(3)

i=1,2,…,m

将式(3)对时间求二次导，可得到矩阵表达式

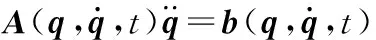
(4)

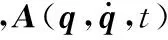
最后需要将约束添加到无约束系统方程中，得到含约束的系统动力学方程。约束在系统中可表现为一种“约束力”，于是含约束的系统动力学方程可表示为

(5)

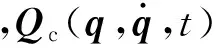
(6)

Udwadia-Kalaba理论考虑了系统约束力在虚位移下做正功、做负功和不做功的情况，拓展了拉格朗日方法。

W=vTc∈Rn

(7)

其中，v为广义虚位移，v∈Rn。理想约束力做的功为

vTQic=0

(8)

非理想约束力做功:

vTQnic≠0

(9)

根据Udwadia-Kalaba理论[1]，系统理想约束力可表示为

Qic=M1/2D+(b-AM-1/2Q)

(10)

系统非理想约束力可表示为

Qnic=M1/2(I-D+D)M-1/2c

(11)

D=AM-1/2

其中，符号“+”表示求矩阵的Moore-Penrose广义逆，I为单位矩阵。向量c由系统性能决定，在实际应用中可通过实验测量得到其各元素数值。

由式(5)～式(8)可得约束系统动力学方程:

M1/2(I-D+D)M-1/2c

(12)

c=0时，系统为理想约束系统，动力学方程为

(13)

式(12)为含约束系统的一般动力学方程，式(13)为含理想约束系统的一般动力学方程。

2 重型汽车动力学等效模型

在重型汽车动力学建模中，所有自由度间的约束都为理想约束，在运用Udwadia-Kalaba理论进行动力学建模时采用式(13)。如按照传统的汽车模型对系统进行动力学建模，自由度之间的约束不好确定，针对此问题本文提出了一种离散化的汽车模型，并用Udwadia-Kalaba理论进行动力学建模。

2.1 重型汽车车身离散化模型

重型汽车中，驾驶员及座椅的质量相对汽车及货物的质量很小，对汽车整车的动力学性能影响较小，可忽略不计，故在不考虑驾驶员及座椅质量的前提下，汽车车身可做图1所示的质量等效。将车身等效为不考虑形状和大小的3×3个按规律分布的离散质量点，并对这些质量点按图1b方法标号。这样就将汽车车身的6个自由的转化为了9个质量点的27个移动自由度，其中B为车身宽度。

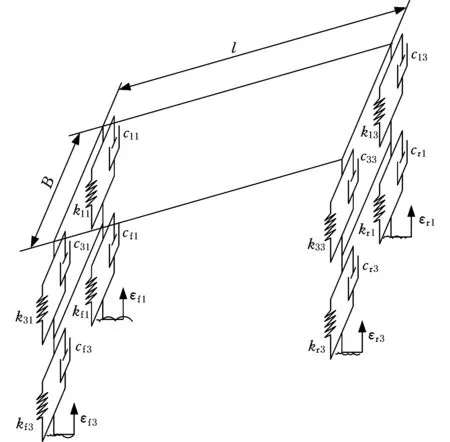
(a)一般车身模型

(b)离散车身模型图1 重型汽车车身等效模型Fig.1 Equivalent model of the body in heavy-duty truck

该模型的转化是以转化前后系统的静态性能和动态性能相当为前提条件的，即转化前后要同时满足静代换条件和动代换条件。设车身总质量为m，俯仰转动惯量为Jxx，侧倾转动惯量为Jyy，转化后车身模型9个点对应的质量分别为m11、m12、m13、m21、m22、m23、m31、m32和m33。

考虑汽车俯仰特性时，为了计算方便，将质点12、22、32设置在与质心同一轴线上，故由质量动代换原理可得

(14)

式中，a为车身质心到车身前端的距离；b为车身质心到车身后端的距离。

为了简化计算，假设汽车前桥与车身前端在同一垂直平面内，汽车后桥与车身后端在同一垂直平面内。由式(14)可得m11+m21+m31、m12+m22+m32、m13+m23+m33。

考虑汽车绕自身中心轴侧倾特性时，为了计算方便将质点21、22和23设置对称轴轴上，故由动代换条件得

(15)

j=1，2，3

又有

(16)

由式(14)～式(16)可得到车身的等效质量矩阵Mb。

由图1中汽车车身的离散化模型可以看到，车身有27个自由度。本文的研究对象为汽车的平顺性，故只需考虑竖直方向的移动自由度，即z向自由度，故车身模型简化为九自由度模型。

在不考虑系统中自由度间约束的情况下，质点11、13、31和33的z向运动形式为在重力、弹簧力和阻尼力共同作用下的受迫振动。质点12、21、22、23和32的z向运动形式为在重力作用下的自由落体运动。

当考虑系统中各自由度之间的约束条件时，由图1可看到，在汽车运行过程中，所有质点都在车身平面内，并且有确定的位置。由3点确定平面可知，有3个质点的运动是自由的，其余质点的运动都可由这3个质点进行约束。本文中假设3个自由质点为11、31和33，可由几何关系得到约束方程

(17)

式中，z11、z12、z13、z21、z22、z23、z31、z32和z33分别为9个质点对应的z向位移。

等效质量矩阵Mb和式(17)共同组成了汽车车身的离散化模型。

2.2 重型汽车车桥离散化模型

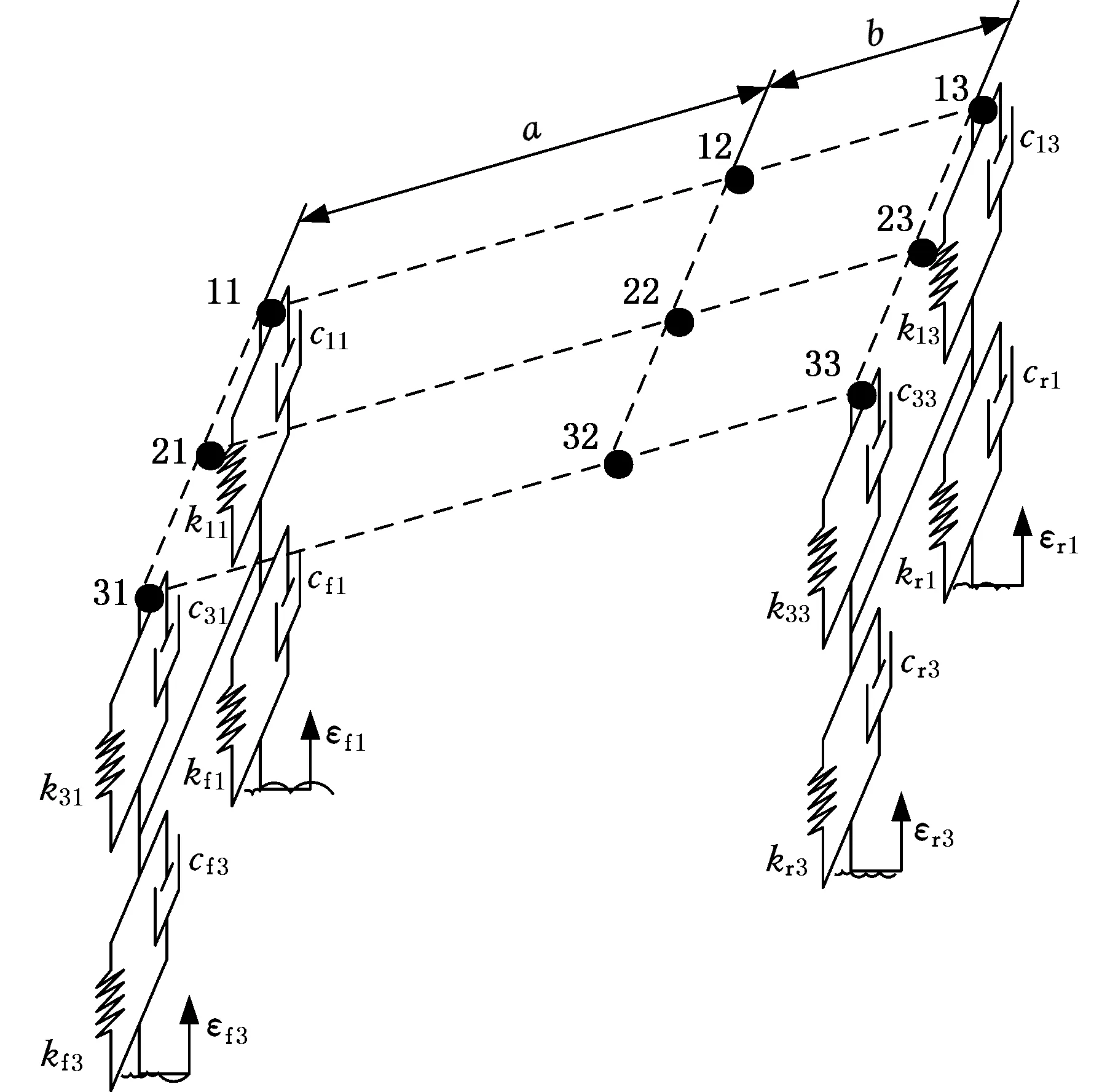
前桥和后桥作为汽车关键零部件，在整车动力学建模中是不可忽略的。一般的汽车动力学模型中，为了简化计算，忽略了车桥的转动惯量，将其等效为两质点，这样便减小了模型的精确性。本文为了使模型更接近实际情况，将车桥的转动惯量考虑到模型中，分别将前桥和后桥等效为3个离散的质点，方法如图2所示，得到汽车整车的等效模型。

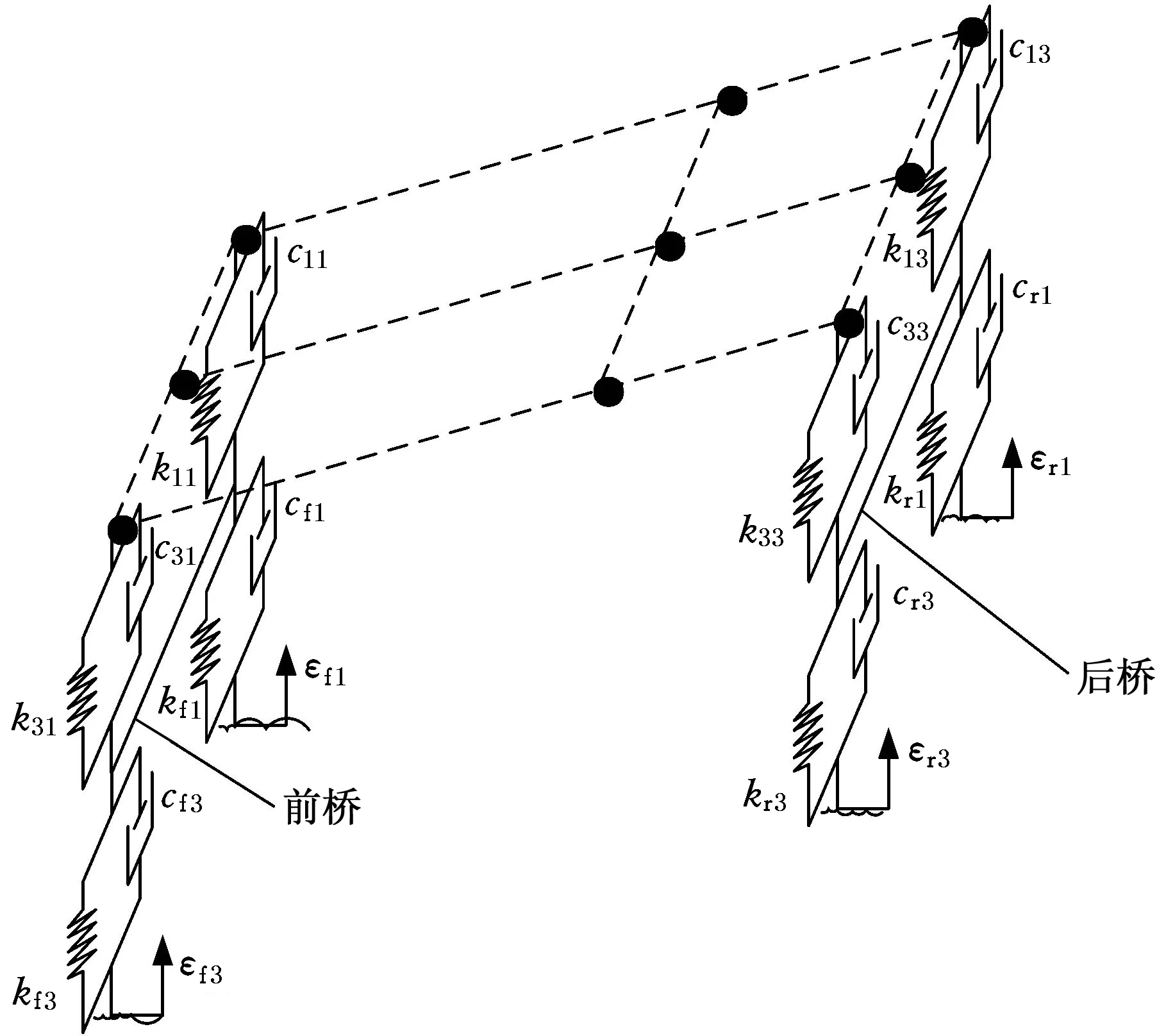
(a)一般车身模型

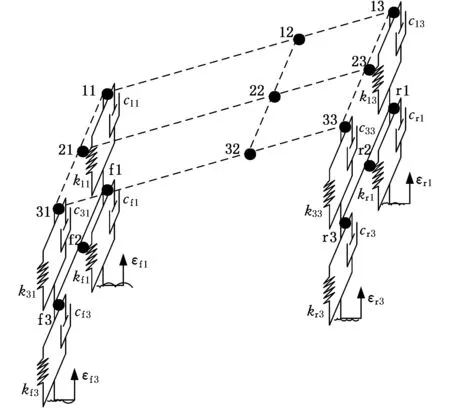
(b)离散车身模型图2 重型汽车车桥等效模型Fig.2 Equivalent model of the axle in heavy-duty truck

对于前桥，设其质量为mf，转动惯量为Ifyy，设转化后模型各个点对应的质量为mfk(k=1，2，3)。为了简化计算，设置点f2位于前桥中心，质点f1和f3分别与质点11和31位于同一竖直线上。由代换条件得

(18)

由式(18)可得前桥的等效质量矩阵Mf。

不考虑约束的情况下，质点f1和f3的z向运动形式分别为在重力、弹簧力和阻尼力共同作用下的受迫振动；质点f2受重力作用，其运动形式为自由落体运动。

考虑约束时，由图2可看到，3个质点始终处于同一直线上，并且有确定的位置，可由几何关系得到约束方程

(zf1+zf3)/2-zf2=0

(19)

式中，zf1、zf2和zf3分别为质点f1、f2、f3对应的z向位移。

设后桥质量为mr，转动惯量为Iryy,同样可得后桥的等效质量矩阵Mr，约束方程为

(zr1+zr3)/2-zr2=0

(20)

式中，zr1、zr2和zr3分别为质点r1、r2、r3对应的z向位移。

等效质量矩阵Mf、Mr和式(19)、式(20)共同组成了汽车车桥的离散化模型。质量矩阵Mb、Mf、Mr和式(17)、式(19)、式(20)共同组成了重型汽车整车系统的离散化模型。

3 系统动力学方程的建立

通过前面的分析得到了一个含15个自由度的汽车整车系统模型，该模型研究对象为汽车的平顺性，忽略了各质点水平面内两个位移自由度的影响。该系统的广义坐标为

q=

[z11z12z13z21z22z23z31z32z33zf1zf2zf3zr1zr2zr3]

首先考虑系统在无约束条件下的运动情况。由分析可得，系统虽有15个自由度，但无约束条件下的运动形式只有两种，即自由落体运动和在路面激励的受迫振动。图3所示为车身上的一个质点与车桥的一个质点的串联模型。

3.对中国特色社会主义的总依据、总布局、总任务进行了创造性论述。报告明确提出：“建设中国特色社会主义，总依据是社会主义初级阶段，总布局是五位一体，总任务是实现社会主义现代化和中华民族伟大复兴。”［1］

由前文描述可知，自由落体运动的质点为12、21、22、23、32、f2、r2，其中，质点12的动力学方程为

(21)

其中，g为重力加速度。同理可得到其他6个自由落体运动质点动力学方程。

质点11和f1、13和r1、31和f3、33和r3的运动形式如图3所示，由拉格朗日定理可得质点对11和f1的动力学方程：

(22)

同理可得其他3对质点的动力学方程。

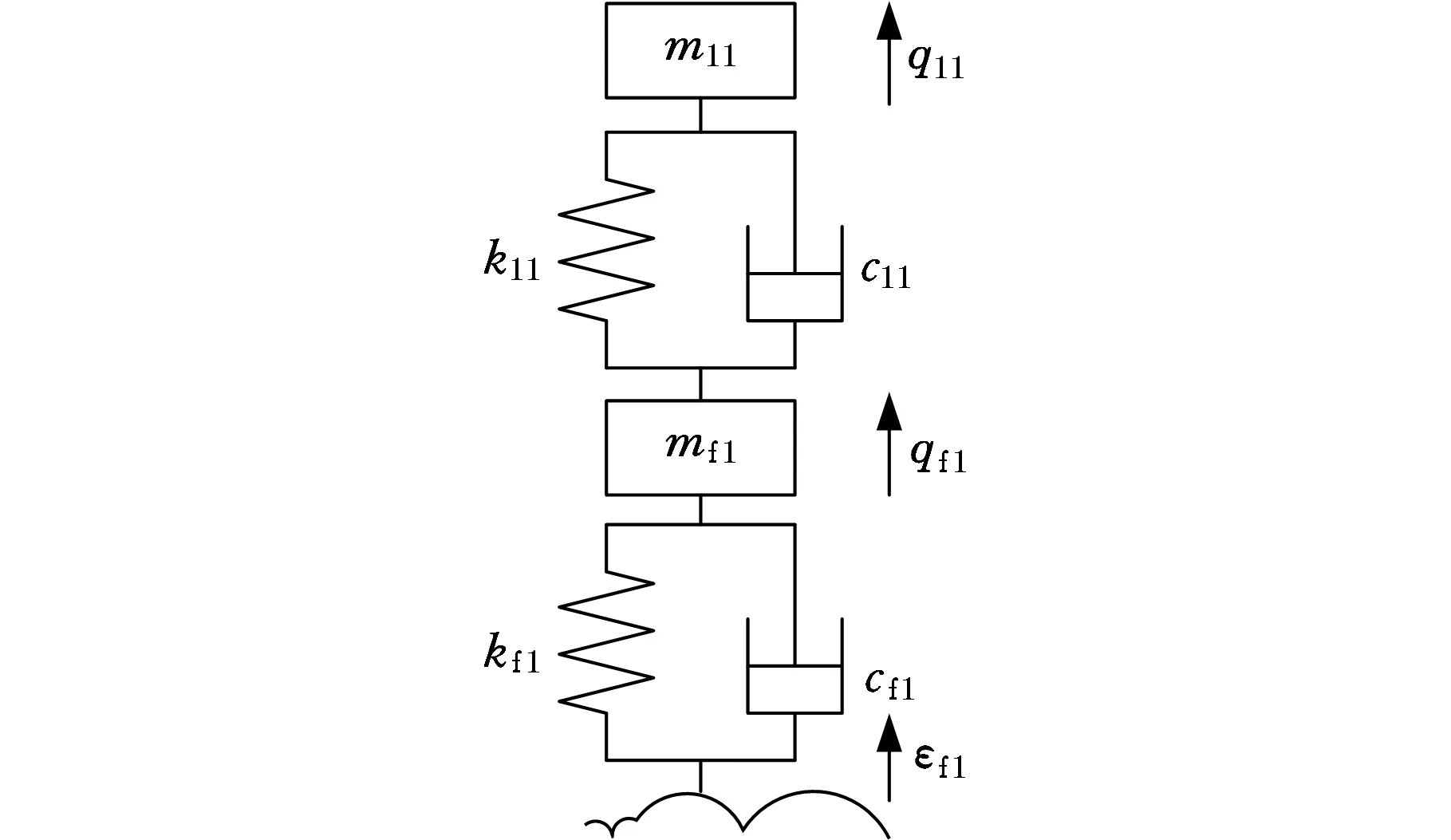
图3 质点11和f1的串联模型Fig.3 Series model of particle 11 and particle f1

将前面得到的15个方程写成矩阵形式为

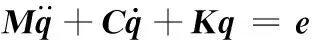
(23)

式中，C为15阶阻尼方阵；K为15阶刚度方阵；e为15维向量。

将式(23)改写为

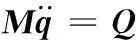
(24)

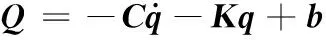
下面考虑系统在约束条件下的运动情况。将式(17)、式(19)、式(20)的8个约束方程写为矩阵形式：

Aq=0

(25)

式中，A为约束矩阵，A∈R8×15。

将式(25)中各元素分别对时间求二次导，由约束方程可知矩阵A中各元素均为常量，故式(25)求导后为

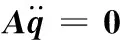
(26)

于是可得约束力

Qc=-M1/2(AM1/2)+(AM-1Q)

(27)

由此可得重型汽车整车系统动力学方程：

(28)

由式(28)可求得各质点的振动情况。

当需要考虑车身某一具体位置的响应时，可建立一空间坐标系，取车身9个等效质点中的任意3个，假设为质点11、31、33，得到车身所在空间平面方程，再由所求位置与3个质点的相对几何关系，易得车身任意一点的响应zt=φ(z11,z31,z33)。

当考虑驾驶员自由度时，首先计算车身上座椅对应位置的响应：

zc=bsz11/B+(1-ls/l-bs/B)z31+lsz33/l

(29)其中，ls为座椅到车身前端的距离，bs为座椅到车身侧面的距离，l为车身长度。将车身上座椅对应位置的响应直接作为激励输入到座椅下的弹簧-阻尼末端，实现驾驶员与整车的耦合，计算方程为

(30)

式中，md为座椅与驾驶员总质量；zd为驾驶员位移；cd为座椅下阻尼器阻尼；kd为座椅下弹簧钢度。

通过式(30)可研究汽车行驶过程中的平顺性。

4 系统仿真及结果分析

对某一具体二轴重型卡车，计算参数如下：m=1500 kg，mf=180 kg，mr=328 kg，Ixx=26 457 kg·m2，Iyy=2450 kg·m2，Ifyy=70 kg·m2，Iryy=114 kg·m2，a=2.85 m，b=1.1 m，B=1.4 m，c11=c31=40 kN·s/m，c13=c33= 4 kN·s/m，k11=k31=251 kN/m，k13=k33= 1 MN/m，cf1=cf3=3.5 kN·s/m，cr1=cr3=12.6 kN·s/m，kf1=kf3=1.1 MN/m，kr1=k33=4.4 MN/m。

用MATLAB软件求解模型，对整车的z向位移进行动力学仿真，通过仿真可预测汽车在各种工况下z向的动态性能。

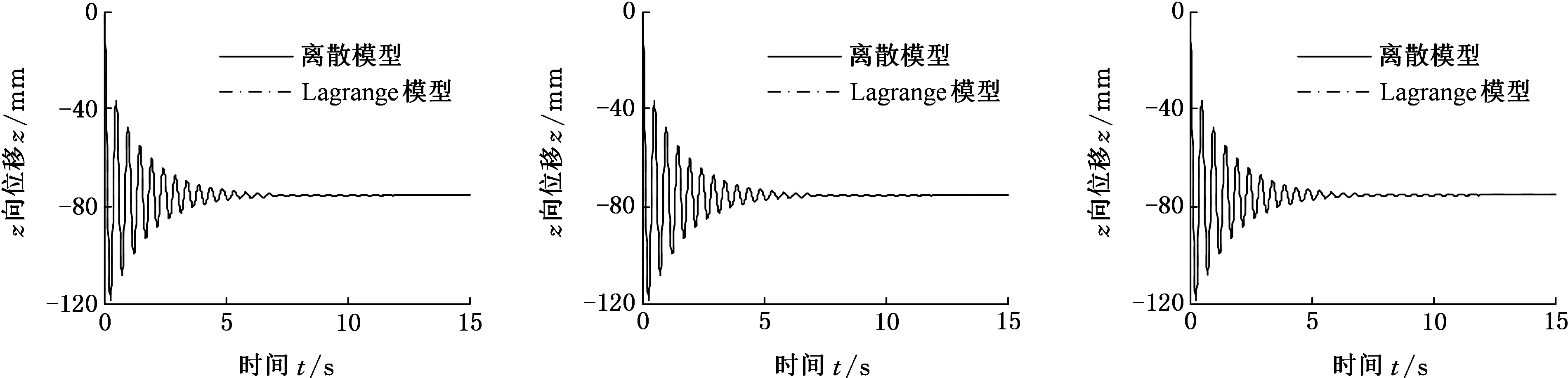
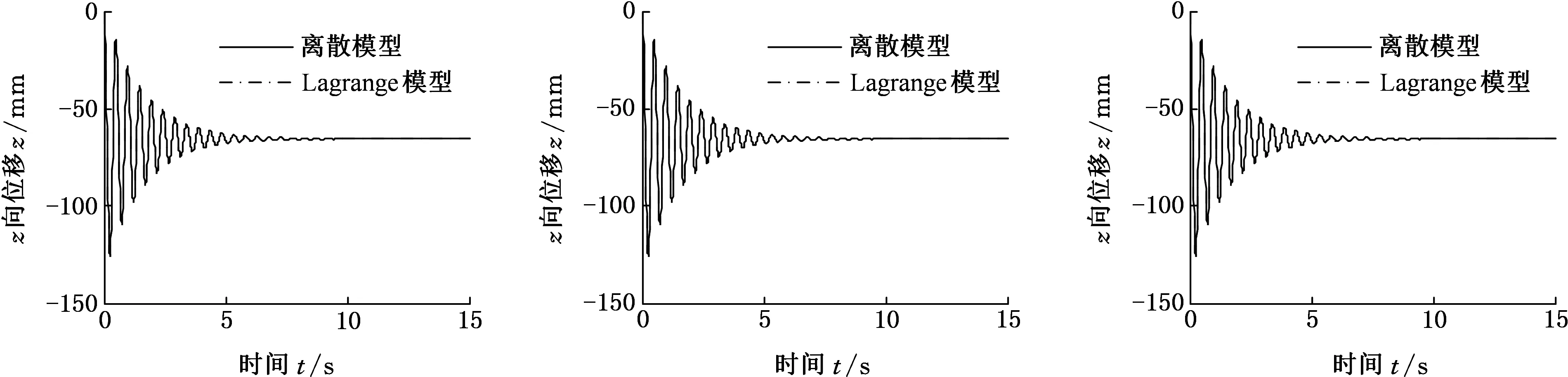
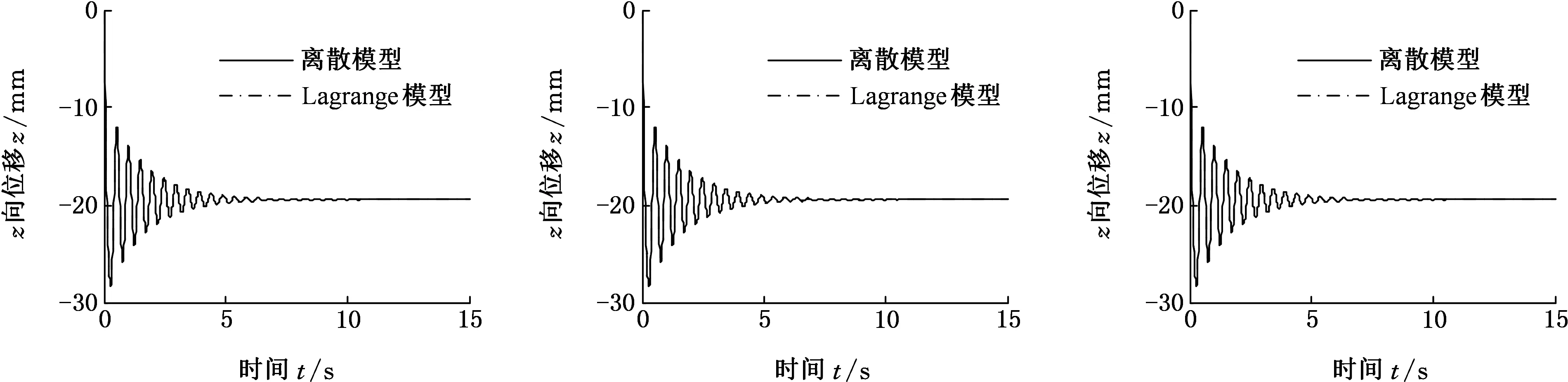
首先进行初始静止状态的仿真，设初始条件：各弹簧处于自由状态；各质点初始位移和速度均为零，加速度为-g。汽车静止不动时，路面对各轮胎的激励为零。在同样的条件下仿真计算Lagrange模型，并将其7个自由度的动态响应通过几何运算转化为车身和车桥上对应13个点的响应曲线，得到各质点运动情况，如图4所示。

由图4可知，两种方法建立的汽车动力学模型在仅考虑重力情况下，计算结果几乎完全重合，证明了离散模型的正确性。根据数据对比可发现，离散模型和Lagrange模型计算结果的差异在0.01 mm以内。这个差异是建模过程中局部简化差异的结果，同时证明相应的简化是合理的。也可通过图4得出汽车运行时各质点的初始位移，可作为后面仿真初值设定的依据。

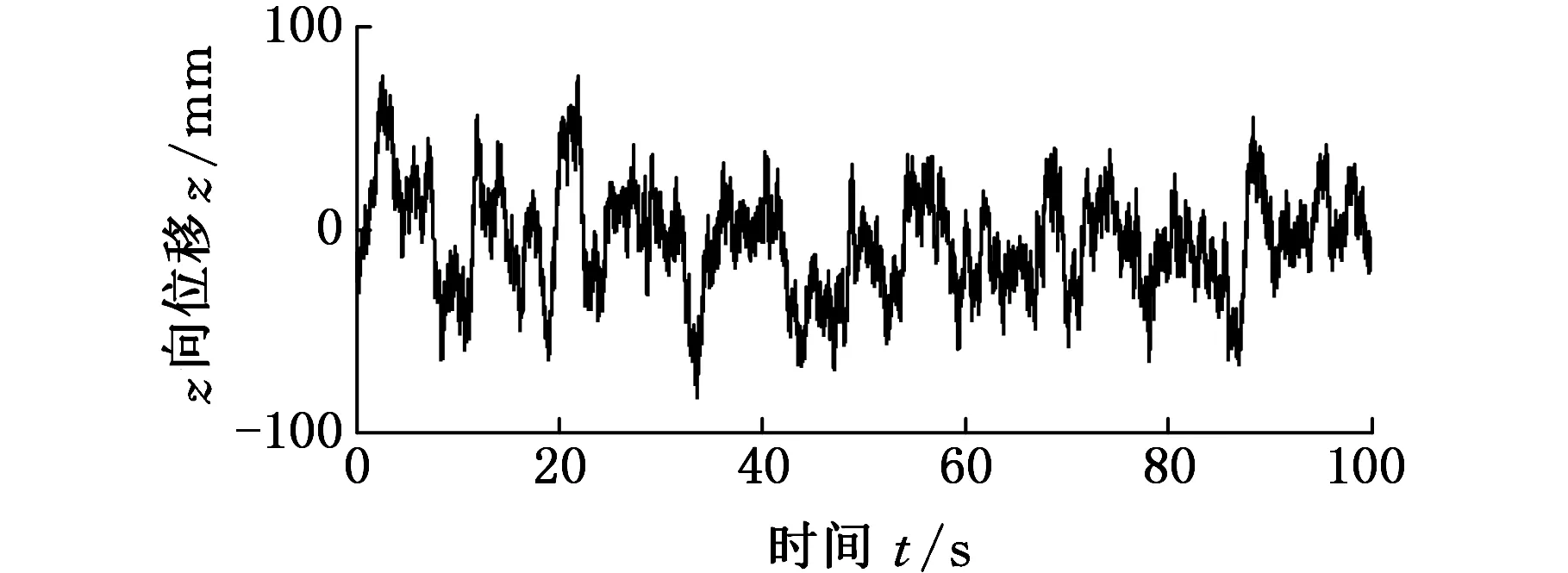
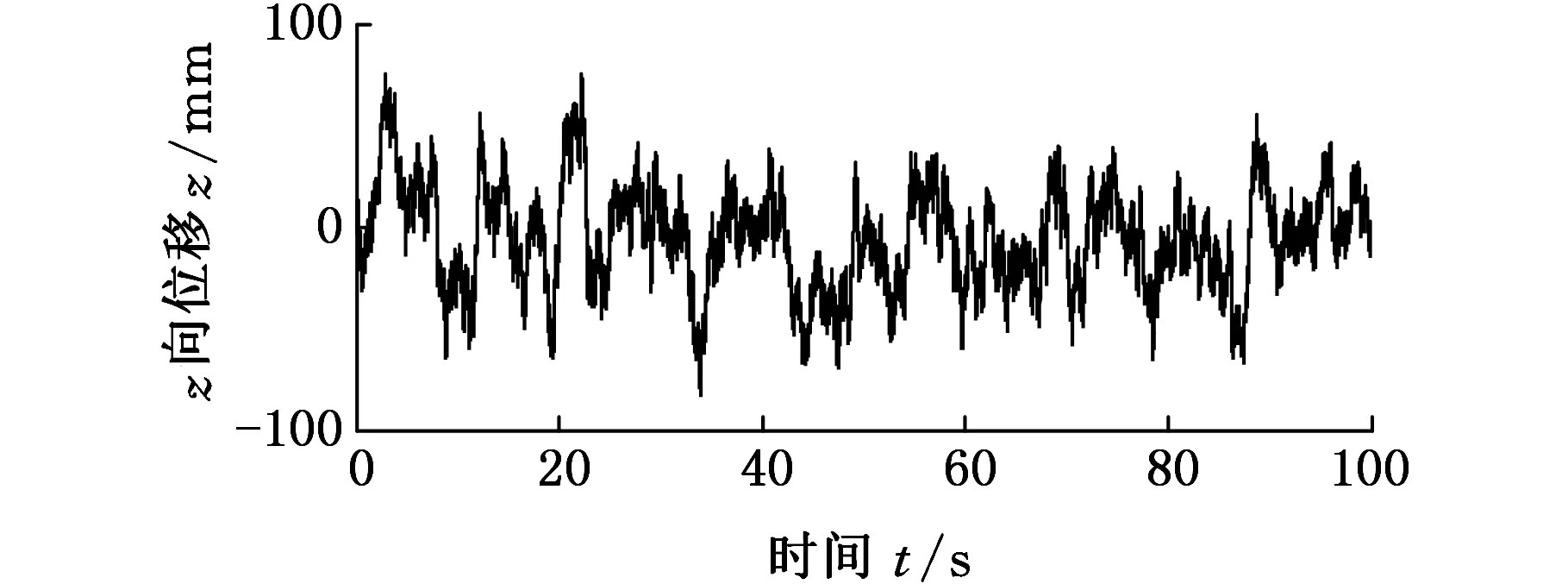
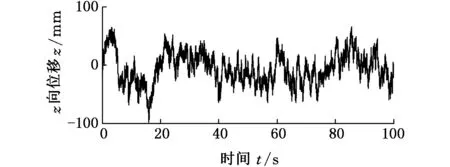
下面采用路面激励分别对离散模型和Lagrange模型进行分析，选择用D级路面，左右轮采用不同的载荷谱，前轮和后轮之间相差一个相位φ，其值可根据车速和前后桥距离计算得到，仿真车速v=10 m/s，根据GB/T7031-2005的规定，生成4个车轮的路面载荷谱，如图5所示。

将载荷谱分别输入离散模型和Lagrange模型进行仿真。图6所示为车身上4个关键点的响应曲线，通过仿真可得到汽车车身的整体运动情况。由于两种模型仿真结果几乎重合，为了显示清楚，将Lagrange模型结果整体向上平移一定距离。

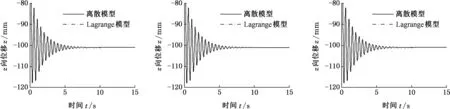
(a)点11(b)点21(c)点31

(d)点12(e)点22(f)点32

(g)点13(h)点23(i)点33

(j)点f1(k)点f2(l)点f3

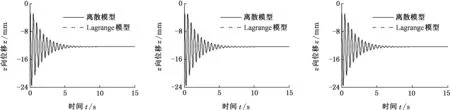
(m)点r1(n)点r2(o)点r3图4 重力作用下各质点位移-时间图Fig.4 Displacement-time diagram of particles under gravity

(a)前桥右侧轮

(b)后桥右侧轮

(c)前桥左侧轮

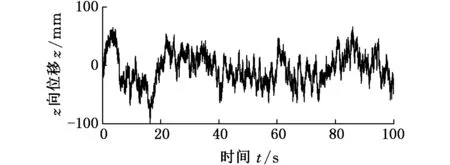
(d)后桥左侧轮图5 4个车轮的位移激励Fig.5 Displacement load of four tires

由图6可知，两种模型在路面载荷作用下，仿真结果完全一致，证明了离散模型的正确性。在仿真开始阶段，设置的初值有一定的差异，故仿真结果也表现出一定差异，当系统稳定运行时，差异消失。

对比图5、图6可看出，路面对轮胎的激励曲线与车身上轮胎对应位置运动曲线趋势一致，由于弹簧和阻尼的作用，车身质点振幅更小，过渡更平顺。后轮与后板簧对应的刚度大于前轮和前板簧，故车身整体后部振动大于前部，此分析结果可作为汽车弹簧、阻尼和质量分布设计的参考依据，优化车身设计。

(a)点11

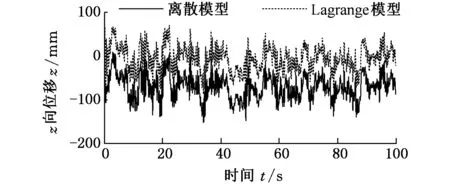
(b)点13

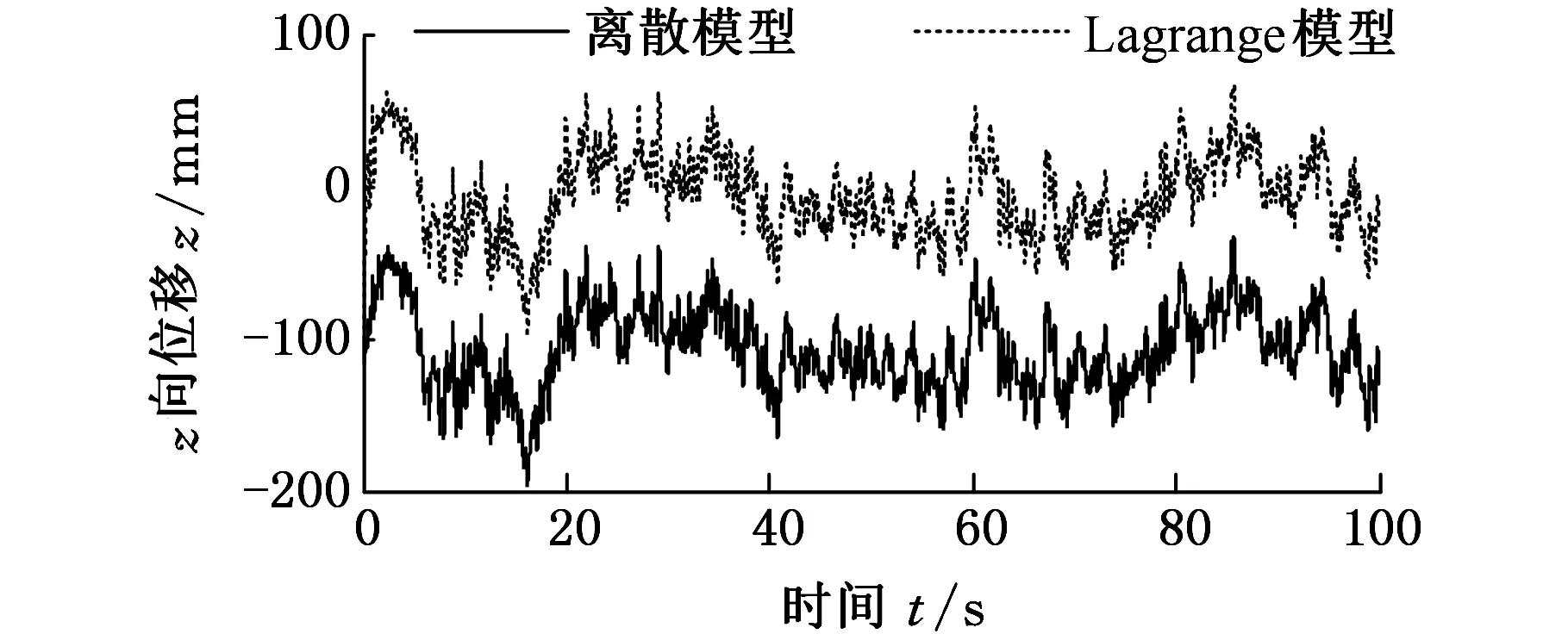
(c)点31

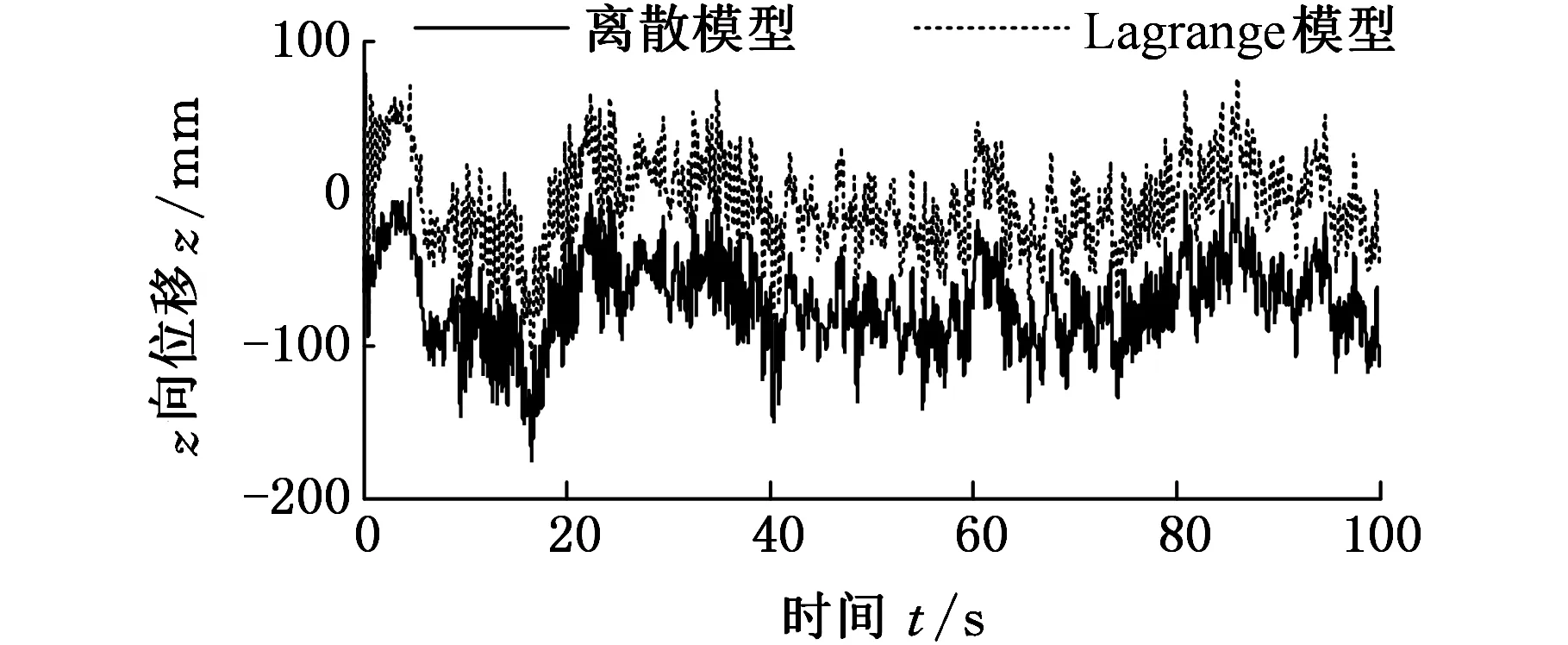
(d)点33图6 车身上四质点时域位移响应Fig.6 Displacement response of four particles on body

图7所示为通过质点11、31和33得到的车身上驾驶员位置的位移曲线，对比图7和图6中各质点的位移响应曲线可看出，质点31的运动特性对驾驶员影响最大。此分析结果将作为式(30)中的激励输入，求解式(30)可仿真得到驾驶员运动特性。

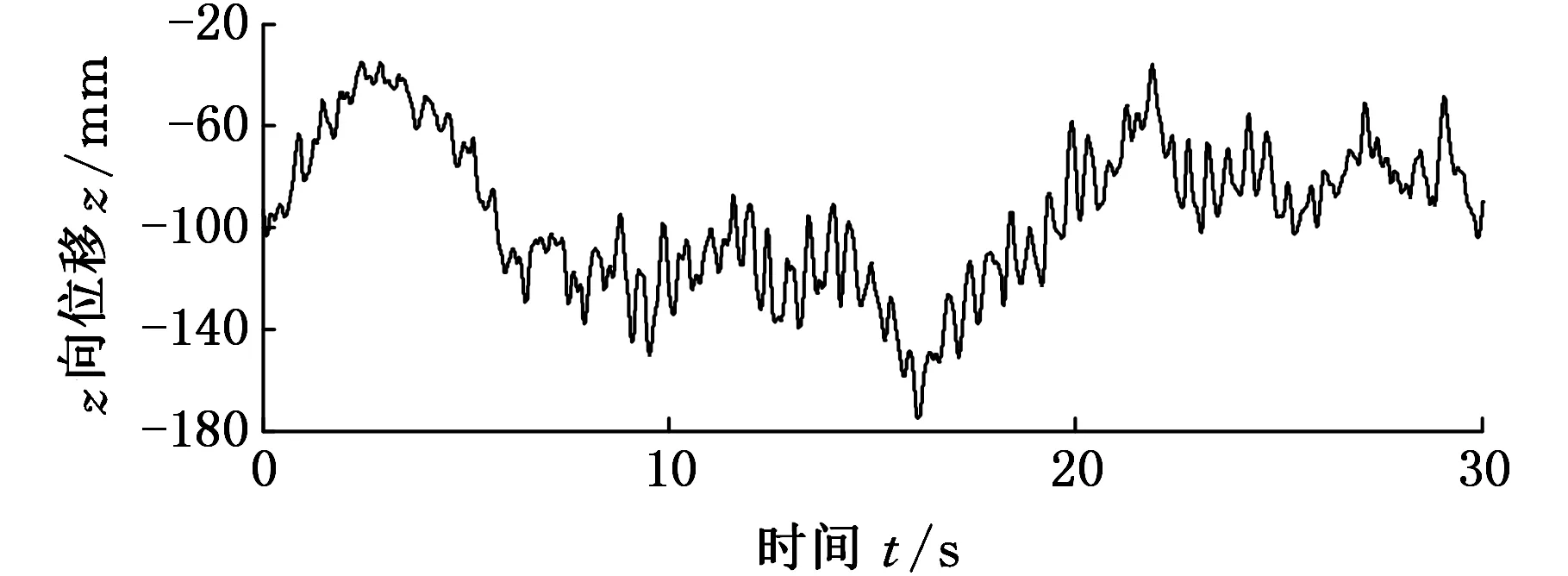
图7 驾驶员座位末端位移激励Fig.7 Displacement load of driver’s seat

图8为驾驶员位移及加速度时域曲线图，通过该结果可对驾驶员动态特性进行分析。从图8可看出，汽车在D级公路上正常行驶过程中，驾驶员z向位移最大幅值为0.15m，加速度变化范围是±10m/s2，幅度和频率都较大，可通过改变相关弹簧和阻尼参数进行优化。此仿真结果可为平顺性分析等汽车动态性能分析提供数据支持。

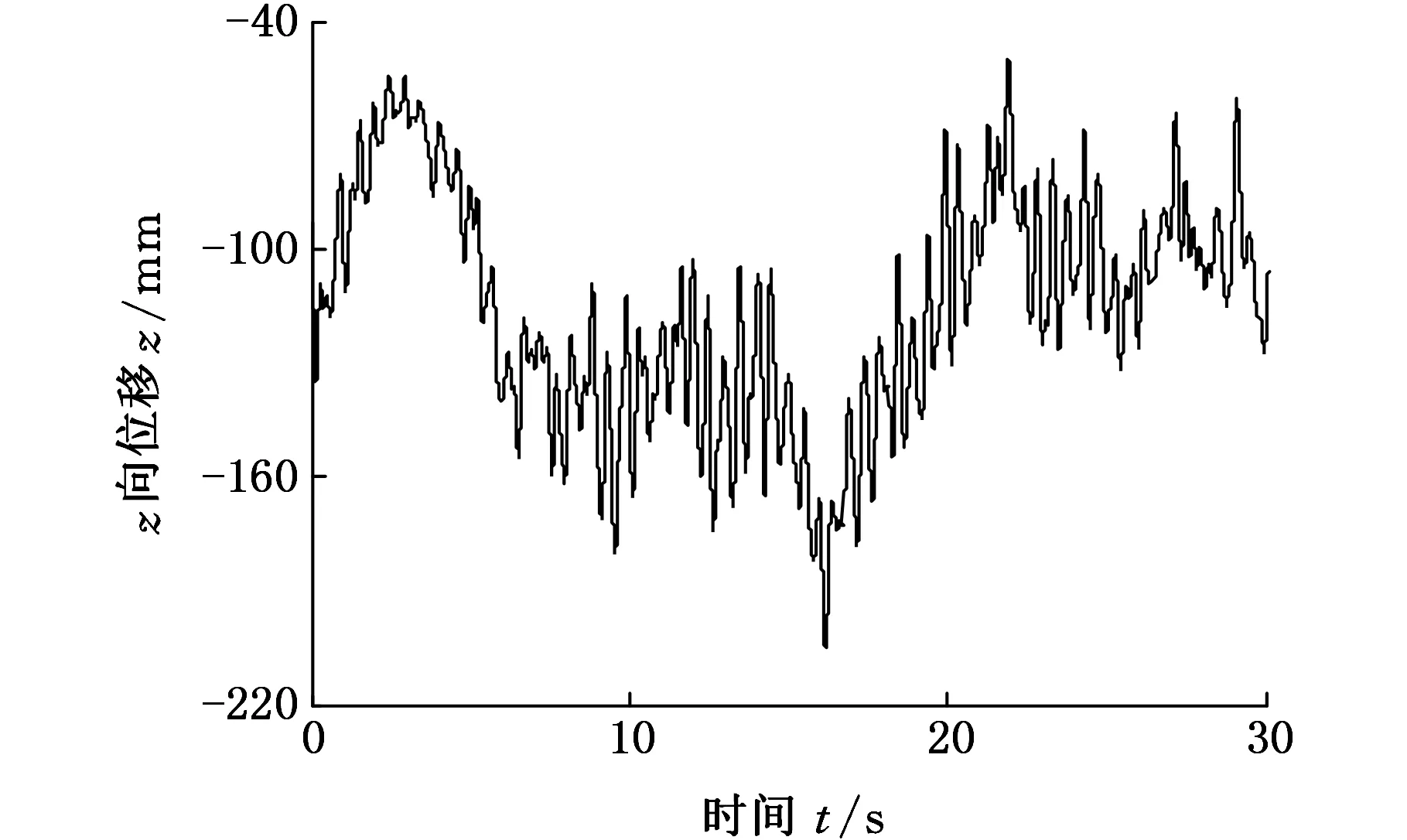
(a)时间-位移图

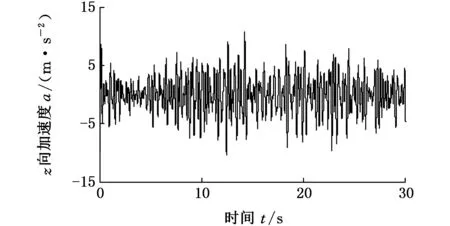
(b)时间-加速度图图8 驾驶员位移及加速度时域曲线图Fig.8 Driver’s displacement and accelerationcharacteristic

5 结论

(1)离散模型与Lagrange模型的对比表明两种建模方法得到的分析结果差别极小，可忽略不计，证明离散该模型是正确的。

(2)通过D级路面激励，得到了车身关键点和驾驶员的动态特性曲线，为后续的分析提供原始数据，还可为汽车弹簧和阻尼器设计提供依据。

(3)本文初始条件的设定以空载仿真结果为依据，这与实际情况有一定的差异，故仿真前0～2s内可能出现振荡，但由于阻尼器的存在，振荡的影响很快会消失。

(4)本文提出的方法也可用于一般乘用车或其他商用车，但当考虑乘客及座椅对整车动力学性能的影响时，可将车身等效质量点中的一个质点转化到座椅对应位置，通过乘客和车身质点串联模型，建立对应的数学模型。

[1]UDWADIAFE,KALABARE.ANewPerspectiveonConstrainedMotion[J].Proc.RoyalSociety, 1992, 439: 407-410.

[2]UDWADIAFE,KALABARE.AnalyticalDynamics:aNewApproach[M].Cambridg:CambridgeUniversityPress, 1996.

[3]UDWADIAFE,KALABARE.ExplicitEquationsofMotionforMechanicalSystemswithNon-idealConstraints[J].J.Appl.Mech., 2001, 68: 462-467.

[4]UDWADIAFE,KALABARE.OnConstrainedMotion[J].Appl.Math.Comput., 2005, 164: 313-320.

[5]UDWADIAFE,PHOHOMSIRIP.ExplicitEquationsofMotionforConstrainedMechanicalSystemswithSingularMassMatricesandApplicationstoMulti-bodyDynamics[J].Proc.RoyalSociety, 2006, 462: 2097-2117.

[6]CHENYH.Second-orderConstraintsforEquationsofMotionofConstrainedSystems[J].IEEE/ASMETrans.Mech., 1998, 3(3): 240-248.

[7]ZHAOH,ZHENSC,CHENYH.DynamicalModelingandSimulationofMulti-bodySystemsbyUsingUdwadia-KalabaTheory[J].Chin.J.Mech.Eng., 2013, 26(5): 839-850.

[8] 甄圣超,赵韩,黄康,等.应用Udwadia-Kalaba理论对开普勒定律的研究[J].中国科学：物理学 力学 天文学, 2013, 44(1): 24-31.ZHENShengchao,ZHAOHan,HUANGKang,etal.OnKepler’sLaw:ApplicationoftheUdwadia-KalabaTheory[J].ScienceChina：Physics,Mechanics&Astronomy, 2014,44(1):24-31.

[9] 方浩,李晓宾,王璐,等.基于路面随机激励的8 自由度整车动力学仿真[J].中国工程机械学报,2007,5(2):167-173.FANGHao,LIXiaobin,WANGLu,etal.DynamicalSimulationof8-DOFVehicleSuspensionBasedonStochasticRoadSurfaceExcitation[J].ChineseJournalofConstructionMachinery, 2007,5(2):167-173.

[10] 管西强,屈求真,张建武,等.四轮转向汽车的模型跟踪变结构控制[J].机械工程学报,2002,38(3):54-58.GUANXiqiang,QUQiuzhen,ZHANGJianwu,etal.Four-wheel-steeringSystemBasedontheVariableStructureModelFollowingControl[J].JournalofMechanicalEngineering, 2002,38(3):54-58.

[11] 张云清,项俊,陈立平,等. 整车多体动力学模型的建立、验证及仿真分析[J]. 汽车工程,2006,28(3):287-291.ZHANGYunqing,XIANGJun,CHENLiping，etal.TheSettingUp,ValidationandSimulationofFullVehicleMulti-bodyDynamicsModel[J].AutomotiveEngineering, 2006,28(3):287-291.

[12] 李杰,秦玉英,赵旗.汽车行驶平顺性建模与仿真的新方法[J].中国机械工程,2009,20(13)：1625-1629.

LIJie,QINYuying,ZHAOQi.ANewMathematicalModellingandSimulationMethodforVehicleRideComfort[J].ChinaMechanicalEngineering, 2009,20(13)：1625-1629.

(编辑 张 洋)

Modeling and Analyses of Heavy-duty Truck Dynamics Based on System Constraints

HUANG Kang1DUAN Songlin1ZHEN Shengchao1XU Rui1XUE Yongchang2

1.School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei,230009 2.Fu Ma Components Co.,Ltd.,Maanshan,Anhui,243100

Aiming at difficulties of building vehicle model, a discrete dynamics model of heavy-duty truck was proposed based on system constraints, and dynamics analyses were made based on the model. Basic theory of the model was from Udwadia and Kalaba’s multi-body dynamics system. The situations that four tires’ loads generated by road were different during normal operations considered. The dynamics characteristics ofzdirection of the vehicle were mainly researched . Though simulations by MATLAB, the graphs of each particles under conditions of unload and load beyond level D were obtained. Compared with the graphs which was generated by Lagrange model, the correctness of the dynamics model was proved, and the simulation graphs of dynamic characteristics of key particles and the driver were analyzed.

heavy-duty truck; system constraint; discrete dynamics system; Udwadia and Kalaba theory; dynamics analysis

2016-03-10

国家自然科学基金资助项目(51505116)

U461.1

10.3969/j.issn.1004-132X.2017.04.017

黄 康，男，1968年生。合肥工业大学机械工程学院教授、博士研究生导师。主要研究方向为计算机辅助公差设计、新型传动设计及理论、齿轮动力学。E-mail:hfhuang98@163.com。段松林，男，1990年生。合肥工业大学机械工程学院硕士研究生。甄圣超，男，1988年生。合肥工业大学机械工程学院副教授。徐 锐，男，1985年生。合肥工业大学机械工程学院博士研究生。薛永昌，男，1867年生。福马汽车零部件有限公司工程师。