波登管2D压力伺服阀反馈装置的特性研究

左希庆 阮 健 李 胜 刘国文 孙 坚

1.浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州,3100142.湖州职业技术学院机电与汽车工程学院，湖州,313000

波登管2D压力伺服阀反馈装置的特性研究

左希庆1,2阮 健1李 胜1刘国文2孙 坚1

1.浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州,3100142.湖州职业技术学院机电与汽车工程学院，湖州,313000

设计了2D压力伺服阀样机模型，利用波登管作为伺服压力反馈单元保持其输出压力恒定。针对波登管在特定范围内随压力线性变形的特性，在分析其变形机理的基础上，建立了数学模型，仿真分析了其受力变形过程，得到其结构参数对线性变形的影响。设计了波登管线性变形实验方案并搭建实验平台，实验结果表明：随着压力的升高，波登管的变形与压力升高基本成线性关系，16 MPa时，其线性变形量为0.7 mm； 动态实验中波登管从受冲击开始到基本稳态耗时约0.9 ms。实验结果与仿真分析基本一致，波登管的特性研究为其在2D压力伺服阀上的应用奠定了基础。

波登管；压力伺服阀； 伺服反馈；静动态特性

0 引言

本文针对波登管在特定范围内随压力线性变形的特性，设计了2D压力伺服阀，将波登管作为压力伺服阀力反馈单元的重要组成部分，首次用在2D压力伺服阀上，来保持压力伺服阀的输出压力恒定，因此，波登管的性能优劣决定了2D压力伺服阀性能的好坏。本文对2D压力伺服阀及波登管的工作原理进行了说明，建立了波登管的数学模型，利用ANSYS软件仿真分析了其受力变形过程，在理论分析和仿真研究的基础上，设计了波登管的实验方案，通过实验验证了波登管的线性变形特性和频率特性。

1 2D压力伺服阀工作原理

1.低压通道 2.低压孔 3.直槽 4. 敏感腔 5.高压孔 6.阀芯 7.高压通道 8.压力腔 9.阀体 10.左弹簧座11.弹簧 12.右弹簧座 13.右端盖 14.卡簧图1 2D压力伺服阀工作原理Fig.1 Working principle of 2D pressure servo-valve

2D压力伺服阀的工作原理如图1所示。它主要由阀体、阀芯、拨杆拨叉传力机构、波登管反馈机构和旋转电磁铁组成。阀芯左侧端面与阀体内孔之间形成圆柱形敏感腔，压力为pc。阀芯右端凸肩端面与阀体内孔之间形成压力腔，因压力腔与进油口连通，其压力为ps。设计时，将阀芯敏感腔的作用面积设计为压力腔作用面积的两倍，因此当pc=ps/2时，阀芯轴向受力平衡，阀芯静止不动。阀体中孔左端内表面上对称地设置一对直槽敏感通道，阀芯左端凸肩外表面对称地设有一对高压孔和一对低压孔，高压孔通过高压通道压力腔连通，而低压孔与回油腔相通，当阀芯装配到阀体中时，阀芯凸肩上的高压孔与低压孔分别位于直槽敏感通道两侧，并与直槽之间形成弓形重叠，两个弓形重叠在压力腔与回油腔之间形成液压阻力半桥。

当阀芯以顺时针方向旋转时(从阀芯右端观察)，低压孔与流动的动能转换成压力能，直槽重叠面积增大，而高压孔与直槽重叠面积减小，敏感腔压力pc降低，而压力腔的压力ps不变，阀芯轴向受力失去平衡，阀芯向左移动。移动过程中，高压孔与直槽之间的弓形重叠面积逐渐增大，低压孔与直槽之间的弓形重叠面积逐渐减小，敏感腔压力随之增大，阀芯在两端敏感腔压力差的作用下轴向滑动。滑动的同时，阀芯在波登管压力负反馈作用下反向旋转，直到高压孔、低压孔与直槽之间的重叠面积相等为止。此时两端敏感腔的压力再次使阀芯轴向受力重新达到平衡，阀芯就在新平衡位置处于稳定状态，出口Q压力保持不变。

当阀芯逆时针方向旋转时，上述变化过程恰好相反，阀芯向右移动到达新的平衡位置。实际应用中，由于扰动因素的存在，其压力不可避免会产生波动，出口Q压力通过阀体上通道与波登管相连，当压力产生波动时，波登管发生相应形变，牵制拨杆拨叉的转动，而拨杆拨叉又直接影响阀芯的旋转，直到二者达到一个稳定的动态平衡，使出口Q的压力保持恒定不变[1]。波登管的变形作用一方面提高了力反馈的响应速度，另一方面也起到了位置反馈(限位)的作用[2-3]。

2 波登管的变形机理

本文所述弹簧波登管形状如图2所示。管子截面为椭圆环状，波登管在压力作用下发生弯曲变形通常就是非圆截面的变形所致。液压传动中的油液具有压力能和动能，这里由于波登管一端封闭，流量几乎可忽略，因此动能的影响可不考虑。具有压力能的油液可对管道壁面产生一定的压强，从而驱动管道弯曲部分产生胀管力，该胀管力可使非圆截面有变圆的趋势,因此波登管受压后产生的拉应力和压应力组成断面力矩，从而引起管子的弹性不平衡。当管子一端固定，另一端自由时，管子将趋于平直，产生形变。其变形机理如图3所示，由管道流体流动的特性可知，胀管力主要驱使波登管在A处产生变形，从而转化为对端部B处的力矩，使波登管发生形变。形变角θ越大，则力矩T也越大，产生的形变位移也越大[4]。

图2 波登管结构图Fig.2 Structure of Bourdon tube

图3 波登管变形机理Fig.3 Deformation principle of Bourdon tube

3 数学模型

C形波登管是压力弹簧管中最简单的形式，为了便于分析，可将2D伺服阀中所用的弹簧波登管的变形近似看作三个C形波登管的总和[5]。

对于C形波登管，在压力载荷作用下，其稳定平衡的标志是总势能最小[6]。利用最小势能原理，即可建立弹簧波登管的数学模型。由于波登管椭圆截面的短半轴b远小于中心线曲率半径R,波登管总势能可看作内势能U1和外势能U2的总和，即

U=U1+U2

(1)

从波登管中截取中心角为dθ的一个微小部分，如图4所示，图中y是波登管中心到管壁的距离，相对于R可忽略不计。假设层间无挤压，管子无限小单元处于二向应力状态，则此势能表达式为

(2)

式中,ε1、ε2分别为在坐标1和坐标2方向的应变；E为弹性模量；μ为泊松比。

图4 波登管截面图Fig.4 Bourdon tube section

因此，整个管子的势能可看作微小单元的积分：

(3)

式中,V为波登管的体积。

由式(3)可得波登管中心角为γ的内势能为

(4)

式中，s为波登管法向截面中线的弧长；h为波登管壁厚；z为微小截面的高度。

由虚位移定理可知[7]，力在位移方向上所做的功W等于外势能，而外势能则等于作用于管上的外力与管子由于变形所引起体积变量的乘积，即

U2=-W=-pΔV

(5)

式中，p为油液作用于管壁的压力。

而R与γ值不变，则体积变量为

ΔV=Rγ(A2-A1)=RγΔA

(6)

式中，A1、A2为波登管变形前后的截面积。

因此，由式(4)和式(5)可得波登管的总势能为

(7)

再根据李兹法可求得中心角γ的变化率与压力p的关系，即弹性特性。利用摩尔积分，确定中心角的变化量后，即可确定波登管的末端位移，如图5所示。

图5 波登管末端位移Fig.5 End displacement of Bourdon tube

力在波登管切向和法向做的功分别为

(8)

(9)

由式(8)和式(9)可得

(10)

(11)

式中，b、a分别为椭圆截面长轴、短轴的长度；α，β为椭圆截面系数；k为波登管主参数。

4 仿真研究

为更清楚地掌握影响波登管的动静态特性及其结构影响因素，在分析其数学模型的基础上，利用ANSYS软件对其进行了仿真研究[8]，其受力云图与仿真模型如图6、图7所示。

表1所示为仿真中所用的结构参数。利用MATLAB将仿真所取得的数据进行拟合分析，得到系统压力与变形位移之间的曲线，如图8所示。由图8可知，波登管在系统压力小于28MPa时，其变形位移与系统压力基本成线性增长趋势，超过28 MPa后，成抛物状增长，不再成比例关系。

图6 波登管受力云图Fig.6 Bourdon tube stress nephogram

图7 波登管受力分析仿真模型Fig.7 Bourdon tube simulation model

半径rd(mm)1.5圆心角(°)270工作压力ps(MPa)28弹性刚度K(N/mm)500油液密度ρ(kg/m3)880泊松比μ0.3弹性模量E(GPa)150

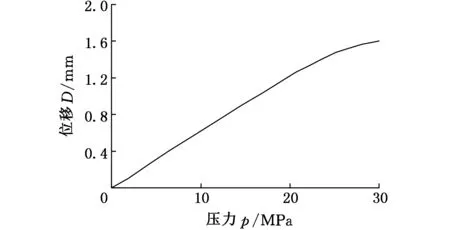
图8 波登管受力变形仿真曲线Fig.8 Bourdon tube deformation simulation curve

利用波登管数学模型在MATLAB/Simulink中搭建动态特性仿真模型[7-8]，在输入一阶跃冲击信号后，得到其频率特性仿真曲线如图9所示。从图9中可以看出，波登管从受冲击开始到基本稳态耗时约0.6ms，可以满足压力伺服阀的动态反馈特性要求。

图9 波登管阶跃响应仿真曲线Fig.9 Bourdon tube step response simulation curve

5 实验研究

为进一步验证波登管作为伺服反馈装置的稳定性，本文设计了静动态实验方案，并搭建了实验台架，实验样机如图10所示。波登管通过特殊焊接技术，一端封闭，一端与油路连接板连接，连接板与油源相通，动态实验中给波登管施加一个突变力来模拟系统压力突变时的状态，通过激光位移传感器检测波登管位移变化情况，从而得到波登管反馈装置的动态响应特性，实验同时也验证了高压下反馈装置焊点的稳定性。

图10 波登管实验样机Fig.10 Bourdon tube prototype

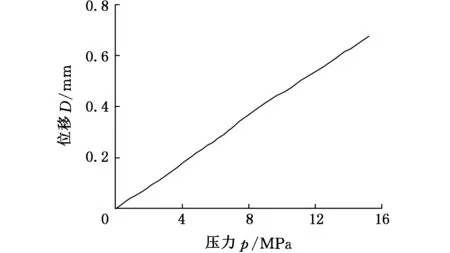
图11 波登管受力变形实验曲线Fig.11 Deformation experiment curve

图12 波登管阶跃响应实验曲线Fig.12 Step response experiment curve ofBourdon tube

静动态实验曲线如图11、图12所示。由图11可知，系统压力由0逐渐增至16 MPa的过程中，波登管的变形位移基本成比例增长，虽然期间有波动，但其波幅在伺服控制的许可范围之内，且系统压力为16 MPa时，波登管变形位移约为0.7 mm，且随着压力的升高，变形并无明显非比例变化趋势。图12表明，受突变力的影响，波登管初始变形较大，但在弹性力的作用下，迅速趋于稳态，从突变到基本稳定所用时间约为0.9 ms, 趋稳后仍有小幅波动，经计算后可忽略，并不影响控制压力的恒定[9]。

6 结论

(1)本文设计了一种2D压力伺服阀，利用波登管作为其伺服反馈装置，从而能精确控制出口压力大小并使其保持压力恒定。

(2)基于2D压力伺服阀工作原理和波登管变形机理，利用管道流体力学理论搭建了波登管的数学模型，应用MATLAB软件仿真分析了其静态变形和动态频率特性。仿真结果表明，波登管作为伺服反馈机构，具有良好的静动态特性,为其在阀上的应用及阀的优化设计提供了理论依据。

(3)波登管静动态实验结果表明，波登管的静态变形特性是线性可控的，变形量可以满足2D压力伺服阀的反馈需要，其复位刚度足以满足动态特性的要求，从突变到稳态所需时间约为0.9 ms，具有良好的静动态特性。

[1] 王积伟. 液压传动[M].北京：机械工业出版社, 2007：34-37. WANG Jiwei. Hydraulic Drive [M]. Beijing: China Machine Press, 2007: 34-37.

[2] 阮健, 裴翔, 李胜. 2D电液数字换向阀[J]. 机械工程学报, 2000, 36(3): 86-89. RUAN Jian, PEI Xiang, LI Sheng. 2D Digital Di-

rectional Control Valve[J]. Chinese Journal of Mechanical Engineering, 2000, 36(3):86-89.

[3] 李胜,阮健,孟彬.2D数字阀滞环颤振补偿技术研究[J].农业机械工程学报,2011, 42(3): 208-214. LI Sheng, RUAN Jian, MENG Bin. Dither Compensation Technology for Hysteresis of 2D Digital Valve[J].Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(3): 208-214.

[4] 翁善臣. 仪表弹性元件设计基础[M].北京：机械工业出版社，1982：142-150. WENG Shanchen. Design Basis of Elastic Instrument Component [M]. Beijing: China Machine Press, 1982：142-150.

[5] 徐芝纶 . 弹性力学[M].北京：高等教育出版社.2006：206-210. XU Zhilun. Elastic Mechanics [M]. Beijing: Academic Education Press, 2006：206-210.

[6] 高耀东,刘学杰. ANSYS机械工程应用精华50例[M].北京：电子工业出版社,2012：192-215. GAO Yaodong, LIU Xuejie. 50 Cases of ANSYS Application in Mechanical Engineering[M]. Beijing: Electronic and Industry Press, 2012：192-215.

[7] 哈尔滨工业大学理论力学教研室. 理论力学(I)[M].7版.北京：高等教育出版社, 2012：72-80. Theoretical Mechanics Teaching and Research Section of Harbin Institute of Technology. Theoretical Mechanics[M]. 7th ed. Beijing: Academic Education Press, 2012：72-80.

[8] 薛定宇，陈阳泉. 高等应用数学的MATLAB的求解[M].3版.北京：清华大学出版社，2014:110-116. XUE Dingyu, CHEN Yangquan. MATLAB Solution of Academic Applied Mathematics[M]. 3rd ed. Beijing: Tsinghua University Press, 2014：110-116.

[9] 盛敬超. 液压流体力学[M].北京：机械工业出版社,1980：124-128. SHENG Jingchao. Hydraulic Fluid Mechanics[M]. Beijing: China Machine Press, 1980：124-128.

(编辑 王旻玥)

Research on Characteristics of Bourdon Tube 2D Pressure Servo-valve Feedback Equipment

ZUO Xiqing1,2RUAN Jian1LI Sheng1LIU Guowen2SUN Jian1

1.Key Laboratory of Special Purpose Equipment and Advanced Processing Technology, Ministry of Education,Zhejiang University of Technology,Hangzhou，310014 2.Department of Mechanical and Electrical Engineering,Huzhou Vocational &Technical College,Huzhou,Zhejiang,313000

A prototype of 2D pressure servo-valve was designed by using Bourdon tube for servo feedback equipment to keep output pressure constant. Aiming at Bourdon tube, which was linearly changed with pressure variations in a particular range, based on the analysis of its deformation mechanism, a mathematical model was established and its deformation processes were simulated, the influences of its structural parameters on linear deformation were presented. The linear deformation experiments of Bourdon tube and its test stand were designed and built, experimental results show that the deformation has nearly linear relationship with pressure risings, the linear deformation range is as 0.7 mm when system pressure is of 16 MPa. In dynamic experiments of Bourdon tube, it took about 0.9 ms from impacts to basic stabilizing. Experimental results and simulated analysis are basically consistent, the research lays the foundation for the applications in a 2D pressure servo-valve.

Bourdon tube； pressure servo-valve； servo feedback； static and dynamic characteristics

2016-04-07

国家自然科学基金资助项目(51405443);浙江省自然科学基金资助项目(LZ13E050002);浙江省科技厅公益技术资助项目(2016C31056);湖州市科技局基金资助项目(2016YZ07)

TH137

10.3969/j.issn.1004-132X.2017.04.013

左希庆，男，1975年生。浙江工业大学机械工程学院博士研究生，湖州职业技术学院机电与汽车工程学院副教授。主要研究方向为流体控制元件及电液数字控制。E-mail：zuoxiqing@yeah.net。阮 健，男，1963年生。浙江工业大学机械工程学院教授、博士研究生导师。李 胜，男，1968年生。浙江工业大学机械工程学院教授、博士。刘国文，男，1976年生。湖州职业技术学院机电与汽车工程学院讲师、博士。孙 坚，男，1989年生。浙江工业大学机械工程学院硕士研究生。