柱形测压铜柱的静态特性分析

王芳， 郭增贵， 朱明武

(1.南京理工大学 机械工程学院， 江苏 南京 210094； 2.国营第641厂， 辽宁 锦州 121017)

柱形测压铜柱的静态特性分析

王芳1， 郭增贵2， 朱明武1

(1.南京理工大学 机械工程学院， 江苏 南京 210094； 2.国营第641厂， 辽宁 锦州 121017)

为了提高铜柱测压的精度，对广泛应用于兵器膛压测量的柱形铜柱静态变形规律进行了研究。在合理假设基础上建立了柱形铜柱静态变形的数学模型，并根据大量的铜柱静态校准数据对模型参数进行了估计。根据此模型进行的仿真计算结果与实验数据能很好地吻合，具有对不同规格铜柱的广泛适用性，能可靠地估算铜柱的静态变形规律。依据该数学模型，对铜柱测压灵敏度随变形量变化的规律和加工尺寸偏差对测压精度的影响两方面进行了计算和分析。结果表明：当铜柱压后高度为原始高度的73%时，铜柱的测压灵敏度最高；铜柱及工作活塞的几何尺寸误差是影响测量不确定度的主要因素，通过提高铜柱的加工精度可以明显提高铜柱测压精度。

兵器科学与技术； 膛压测量； 测压铜柱； 塑性测压器； 静态特性

0 引言

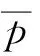
1 铜柱静态变形的数学模型

1.1 铜柱静态变形的数学模型建立

尽管镦粗研究的最终结果不能用于铜柱的分析计算，然而其研究的某些方法和结论却有可借鉴之处。影响墩粗过程的要素主要是材料的力学特性、被镦粗体的原始尺寸(直径d0和高度h0)和试件端面与压头之间的摩擦应力。其中摩擦力是铜柱变形过程复杂化的重要原因。

大量柱形铜柱静态校准数据的分析结果表明，可以把原本复杂的三维变形过程简化为“准一维变形”过程。建模的基本假设及其根据如下：

1)所有铜柱的材料力学特性是高度一致的。因为铜柱都采用高纯度的无氧铜，并经过严格的多次冷拔、退火处理，材质的均匀性和一致性远远超过一般的工业用金属材料。

2)摩擦力对于各种规格的铜柱影响基本相同。因为铜柱测压器的材料、加工精度、表面质量等影响摩擦力的因素，几乎都得到严格的控制。

3)铜柱变形过程中，其形状始终保持为圆柱形，即忽略腰鼓形的影响。

4)铜柱变形过程中体积不变。因为高纯度的无氧铜的弹性极限很低(约30 MPa)，相应的应变值小于3×10-4；而铜柱的工作应变却较高，达0.1～0.55. 因此弹性变形引起的体积变化可以忽略，而塑性变形过程是体积不变的。

根据以上假设，可以列出以下基本方程：

力平衡方程

pS=σSc,

(1)

体积不变关系

(2)

应变与瞬时高度关系

(3)

弹性恢复关系

Eεe=σe,

(4)

式中：p是压力(Pa)；S是活塞工作面积(m2)；σ是铜柱平均应力(Pa)；Sc是铜柱截面积(m2)；h是铜柱受压后的瞬时高度(m)；d0、h0分别为铜柱的原始直径和原始高度(m)；ε是铜柱的应变值；E是铜柱材料的杨氏模量(Pa)；εe是铜柱卸载过程的弹性应变；σe是铜柱卸载过程的应力(Pa)。

(1)式、(2)式联立可得

(5)

(4)式、(5)式联立并考虑到弹性恢复过程的总应变值为

(6)

式中：Δ是铜柱卸载过程的弹性恢复量(m)；hc是铜柱卸载后的残余高度(压后高度)。可得

(7)

(3)式、(6)式、(7)式联立可得铜柱在加压p时的瞬时应变值：

(8)

铜柱静态校准的结果是获得一组关于压力与压后高的数据对(pi,hci),i=1,2,…,n. 利用(5)式和(8)式，可以计算得到相应的瞬时应力、应变数据对(σi,εi),i=1,2,…,n. 对7种规格的柱形铜柱(φ3 mm×4.9 mm,φ4 mm×6.5 mm,φ5 mm×8.1 mm,φ6 mm×9.8 mm,φ8 mm×13 mm,φ4 mm×8 mm,φ3.5 mm×8.75 mm)，38个批次的313个数据对[8]，进行了计算分析，结果表明，用一个3阶多项式可以很好地描述柱形铜柱的应力、应变关系：

σ(ε)=2.458×109ε3-3.233×109ε2+
1.592×109ε+5.293×107.

(9)

拟合曲线的相关系数为0.992 4，标准差为4.1 MPa. 图1清楚地表明了拟合曲线与上述7种不同规格铜柱的实验数据符合得很好。应当指出的是，根据(5)式和(8)式计算所得的应力、应变值以及由此而来的应力、应变关系式(9)式，并不是材料真正的应力和应变关系，而是隐含了对摩擦力等影响因素进行了修正的等效应力和等效应变的关系式。

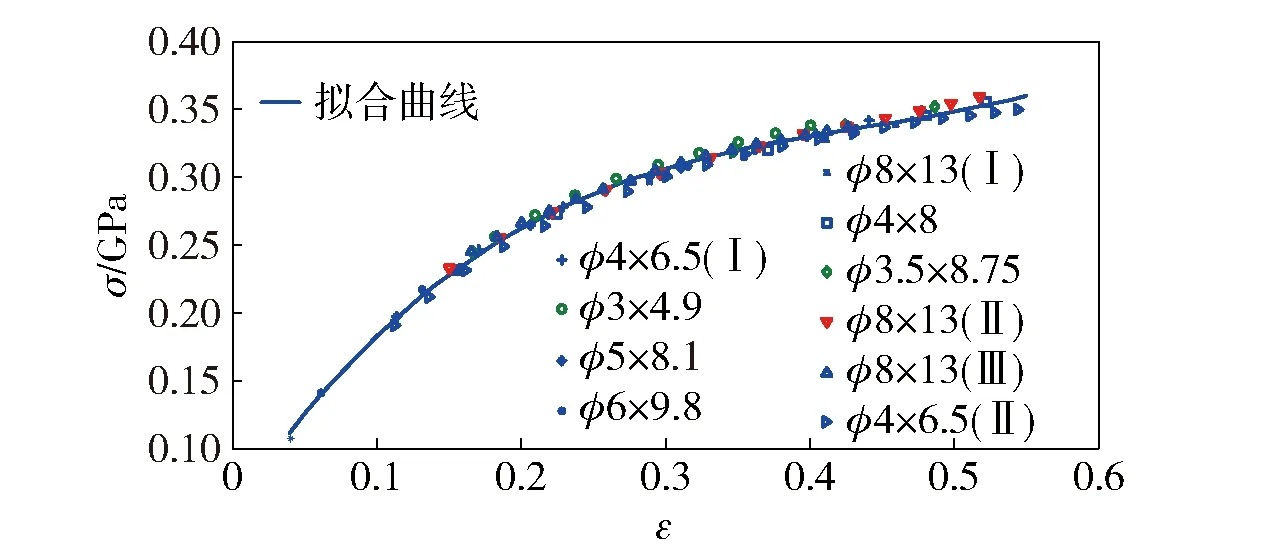
图1 铜柱材料的塑性应力、应变曲线Fig.1 Plastic strain-stress curve of copper cylinders

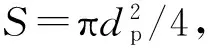
(10)

式中的系数a0、a1、a2、a3可以根据以上分析计算获得，但按照(10)式直接利用7种不同规格铜柱的多批次静态校准数据(共百余组校准数据)进行拟合，得到其中的系数应该是更可靠的。计算结果如下：a0=2.516×109,a1=-6.602×109,a2=7.659×109,a3=-3.528×109.

根据(10)式不难求得铜柱的压力系数k=dp/dhc，符合

(11)

图2是按照(10)式和(11)式绘出的统一的柱形铜柱特性曲线，图2(a)和图2(b)两条曲线适用于各种不同规格的柱形铜柱。

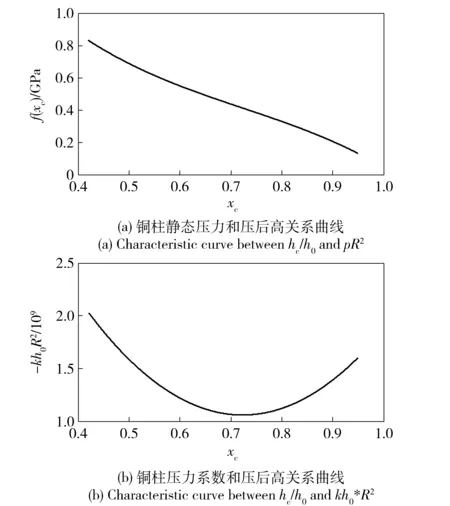
图2 统一的柱形铜柱工作特性曲线Fig.2 Unified characteristic curves of copper cylinders

1.2 柱形铜柱特性的计算分析和验证

根据以上数学模型，给定基本参数d0、h0、S，并合理设定一系列铜柱受压后的相对压后高xi(i=1,2,…,m)，代入(10)式可得到一系列数据f(xi). 再代入某种铜柱的R值，可计算出pi,并根据xc求得压后高值hci，从而可以得到各种铜柱的工作特性曲线。

图3是7种不同规格铜柱的计算结果与实验数据的关系图。图3中的曲线和数据点都相当吻合，说明(10)式对铜柱分析具有很好的工程精度和广泛的适用性。

图3 7种柱形铜柱的工作特性计算结果Fig.3 Calculated results of seven different copper cylinders’ parameters

2 柱形铜柱静态特性分析

利用(10)式和(11)式还可以分析铜柱多方面的工作特性，下面仅从铜柱压力系数的特点和加工尺寸偏差对测压精度的影响两方面进行初步分析。

2.1 铜柱压力系数的变化规律

按(11)式不难证明，k的最小值出现在xc=2a2/6a3=0.73附近。即在hc=0.73h0附近灵敏度最高(见图2(b)曲线)。这一点与实际数据非常吻

合。由于铜柱的实际压后高度在(0.45～0.9)h0范围之内，这说明铜柱的灵敏度在其量程内呈两端低、中间高的特点，所以任何柱形铜柱工作在其量程的中间偏上的压力处是最佳的。

2.2 铜柱及活塞尺寸偏差对测压精度的影响

铜柱及活塞的主要几何尺寸如铜柱的原始直径d0和高度h0及活塞直径dp的加工误差显然对铜柱的测压误差是有影响的，然而过去由于缺乏适用的数学模型，一直无法定量分析其中的关系。而上述(10)式建立了这些参数及压力之间的数学模型，为定量分析提供了基础。表1是根据(10)式求得的当误差源分别来自于铜柱的原始直径d0和高度h0及活塞的直径dp，输出分别为压力p和压后高度hc时误差传递的灵敏系数。表1中相对误差传递的灵敏系数除了3个常系数(k2,k3,k4)之外，其他3个都与k1有关。分析可知k1随相对压后高度xc增大而急剧增大，说明原始高度h0的相对误差对测压的相对误差影响随着压力减小而急剧增大。而k2、k3都是常数，所以d0、dp的误差对测压精度的影响是不随压力大小变化的。而k5、k6随xc的变化相对较小。

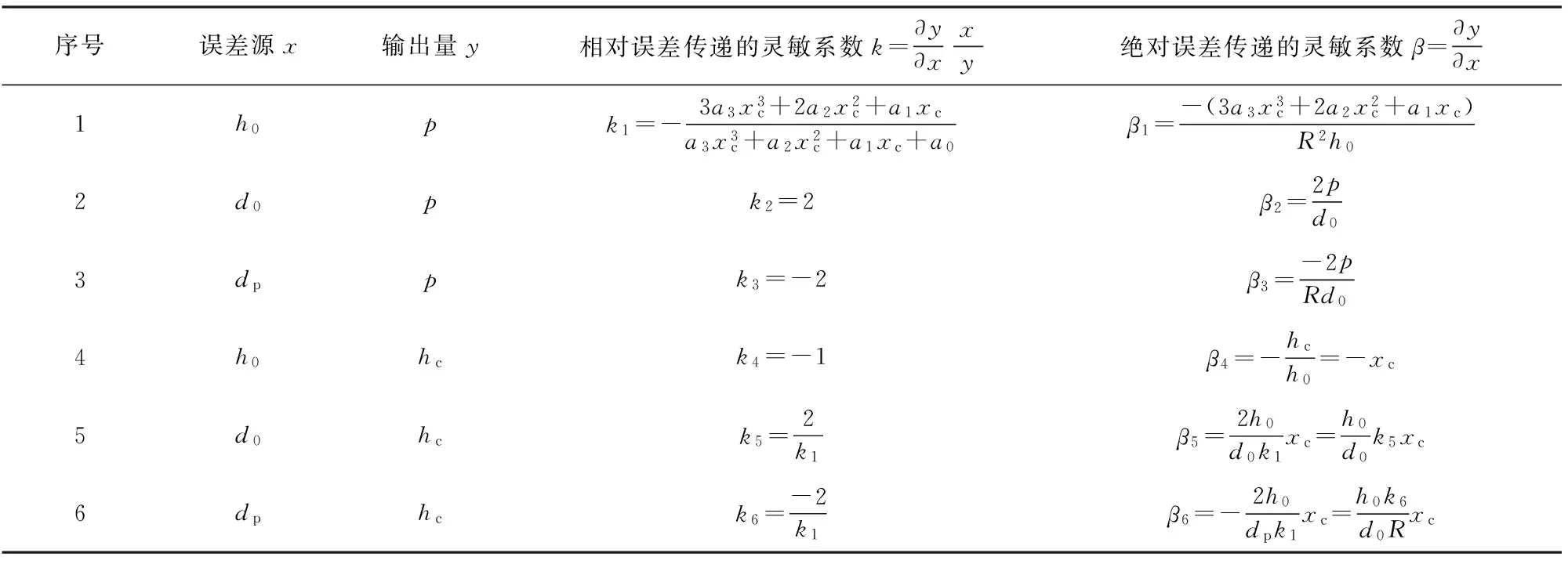
表1 柱形铜柱几何参数的误差传递灵敏系数

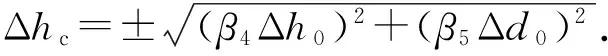
由以上计算结果可知：第一，铜柱原始直径d0公差的影响大于铜柱原始高度h0的公差；第二，同样的尺寸公差对小尺寸铜柱的影响较大；第三，h0公差的影响随xc的增大而增大，即对小压力测量的影响大；d0公差的影响随xc的增大而减小，即对小压力测量的影响小。最后，由计算偏差与允许偏差之比可以看出，铜柱原始尺寸偏差是标定压后高度偏差的主要成因，由此可以得出结论：提高铜柱加工精度可以明显地提高铜柱测压的精度。利用(10)式和(11)式还可以进行多方面的分析，本文限于篇幅不再赘述。

表2 铜柱加工误差对压后高度的影响

3 结论

1)本文从工程应用出发，建立了柱形铜柱的半经验数学模型，通过与大量实测数据的比较表明，该模型具有足够高的工程计算精度，和对不同规格铜柱的广泛适用性。

2)分析表明，铜柱压后高度等于原始高度的73%时灵敏度最高，合理的工作量程应尽可能对称地分布在这个压后高值的两侧。

3)目前我国的铜柱及工作活塞的几何尺寸误差是影响测量不确定度的主要因素，通过提高铜柱的加工精度可以明显提高铜柱测压精度。

4)利用本文的数学模型还可以对柱形铜柱的优化设计、合理生产及科学使用提供更多的帮助，相关的研究工作尚待继续进行。

References)

[1] 王芳, 孔德仁, 李丽萍. 静标测压铜柱的静动差修正方法研究[J]. 计量学报, 2016, 36(2): 158-161. WANG Fang, KONG De-ren, LI Li-ping. Research on the correction method of dynamic-static error for the statically calibration of the manometry copper cylinder[J]. Acta Metrologica Sinaca, 2016, 36(2):158-161. (in Chinese)

[2] 彭大署. 金属塑性加工原理[M]. 第2版. 长沙: 中南大学出版社, 2014. PENG Da-shu. Principles of metal forming processes[M]. 2nd ed. Changsha: Central South University Press, 2014. (in Chinese)

[3] Johnson W, Mellor P B. Engineering plasticity[M]. London: Van Nostrand Reinhold Company, 1973.

[4] 刘助柏, 倪利勇, 刘国晖. 大锻件形变新理论新工艺[M]. 北京: 机械工业出版社, 2009. LIU Zhu-bai, NI Li-yong, LIU Guo-hui. New theory and new technology of deformation of large forgings[M]. Beijing: China Machine Press, 2009. (in Chinese)

[5] Унксов Е П,Сафаров Ю С,Вентер Р Д, et al. Теория Пластических Деформаций Металлов[M]. Москва: Машинострение, 1983.

[6] 田贵义, 李佩华. 铜柱测定膛压装置动态误差分析[J]. 测试技术学报, 2004, 18(增刊):121-124. TIAN Gui-yi, LI Pei-hua. The dynamic error analyses about the copper columniation measuring pressure equipment in interior ballistics[J]. Journal of Test and Measurement Technology, 2004, 18(S):121-124. (in Chinese)

[7] 杨丽侠, 张邹邹, 靳建伟, 等. 塑性测压静态校准用标准铜柱研究[J]. 计测技术, 2013, 33(4):33-36. YANG Li-xia, ZHANG Zou-zou，JIN Jian-wei, et al. Study of standard copper cylinders for static calibration system of plastic pressure measuring Elements[J]. Metrology and Measurement Technology, 2013, 33(4):33-36. (in Chinese)

[8] 伍鹰. 测压铜柱静动态特性分析[D]. 南京: 南京理工大学, 1991. WU Ying. The analysis of the static and dynamic characteristics of copper cylinder[D]. Nanjing: Nanjing University of Science and Technology, 1991. (in Chinese)

Static Characteristics of Copper Cylinders for Chamber Pressure Measurement

WANG Fang1, GUO Zeng-gui2, ZHU Ming-wu1

(1.School of Mechanical Engineering,Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China;2.State-owned Factory 641, Jinzhou 121017, Liaoning, China)

Copper cylinders as a sensing element of crusher gauges are widely used for measuring the peak pressure in weapon chamber. In order to improve the measuring accuracy, a new mathematic model is proposed to investigate the static deformation of copper cylinders. The model parameters are estimated based on calibrated data.The calculated results are in good agreement with the experimental results. This model can be well applied to estimate the static deformation law of copper cylinders, and has wide applicability to different specifications of copper cylinders. According to the mathematical model, the variation of copper cylinder pressure sensitivity with deformation and the influence of machining dimension deviation on the accuracy of pressure measuring are calculated. When the height of copper cylinder after compression is 73% of its original one, the pressure sensitivity of the copper cylinder is the highest. The geometric dimension tolerances of copper cylinder and piston are the main factors which affect the pressure measurement uncertainty. The pressure measuring precision of copper cylinders can be improved by improving the machining precision obviously.

ordnance science and technology; chamber pressure measurement; copper cylinder; crusher gauge; static characteristic

2016-07-12

国防科技工业基础科研计划项目(2014年)

王芳(1966—)，女，博士研究生。E-mail: wangfang@mail.njust.edu.cn； 郭增贵(1931—)，男，研究员。E-mail: guosong816@sina.com

朱明武(1933—)，男，教授，博士生导师。E-mail: zhumw105@126.com

TJ012.1+6

A

1000-1093(2017)02-0412-05

10.3969/j.issn.1000-1093.2017.02.028