集中供热系统的供水温度预测与控制研究
隋修武,程国栋,胡秀兵,徐立伟
(天津工业大学机械工程学院,天津市现代机电装备技术重点实验室,天津 300387)
0 引言
集中供热系统由热源、换热站、用户和各环节相连的热网组成,其中换热站包括一次网供热回路、二次网供热回路及中间换热器[1]。为保证用户供暖质量,对二次网供水温度的控制至关重要。文献[2]提出了神经网络模型预测算法,预料和控制未来时刻的加热炉温度值,解决了步进梁加热炉温度控制的非线性和滞后性问题。文献[3]采用了基于单神经元动态模型的二次网供回水温度控制方案,很好地适应了环境变化和模型不确定性。文献[4-6]指出了模糊控制算法是一种基于规则的控制,不需要建立被控对象的精确的数学模型,尤其适合于非线性、时变及纯滞后系统的控制。借鉴前者的思想,本文针对集中供热系统的复杂特征,构建RBF神经网络预测模型并设计一种自适应Smith-Fuzzy-PID控制器,控制系统的输入设定值即为预测的二次网供水温度值,通过对二次网供水温度闭环控制保证用户供暖质量。
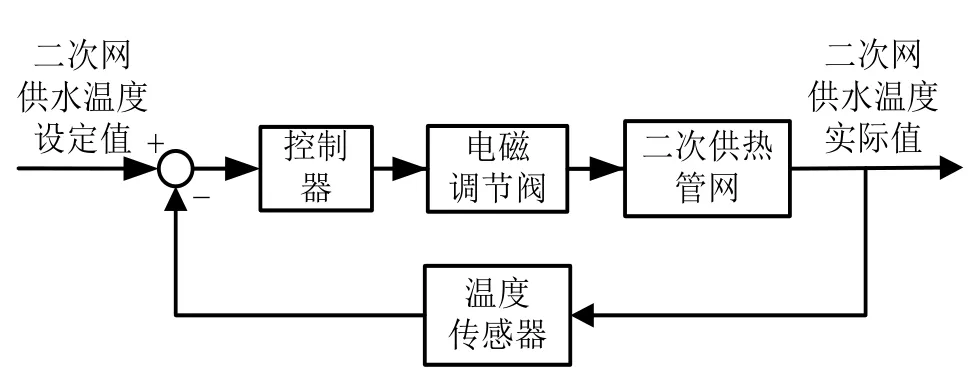
图1 二次网供水温度控制系统Fig.1 Control system of secondary net supply water temperature
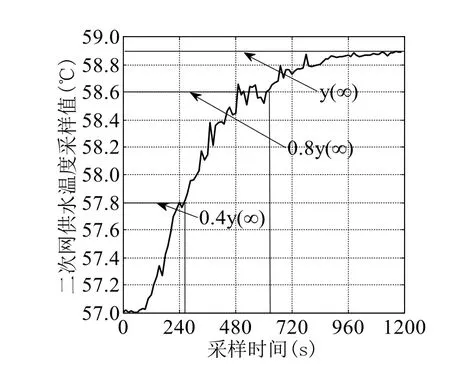
图2 二次网供水温度阶跃响应曲线Fig.2 The step response curve of secondary net supply water temperature
1 供水温度控制系统及模型的建立
供热系统的质调节方式是通过控制一次网流量大小来控制整个系统的。图1所示为二次网供水温度控制系统。为使一、二次网的热力水利良好运行,系统需要设计一种控制器,将二次网供水管道温度传感器采集的信号反馈到控制器内,经运算后将控制信号传给电磁调节阀,调节其开度调控二次网供水温度。
由于实际运行的供热系统相当复杂,本文拟通过实验来获得二次网供水温度动态特性曲线,再用两点法求取相关特性参数[7]。对天津市某一供热站,实验操作如下:某一时刻迅速改变一次网供水阀门开度由45%开至70%,一次网供水流量由45.58(t/h)升为54.61(t/h),观察记录二次网供水温度变化值,采样周期为12 s,共采100次得到1200 s的温度数据,建立二次网供水温度阶跃响应曲线如图2。
根据供热阶跃响应特点,设其数学模型为

两点法[8]的原理为:在阶跃响应曲线标记得到最终稳态值y(∞),分别估计出到达0.4y(∞)和0.8y(∞)的时间t1和t2,根据近似公式(2)、(3)、(4)计算各个特性参数。

(2)式中,q为输入值。令q=27,由7可得,t2=620s,滞后时间τ=70,代入(2)、(3)、(4)式得被控对象的数学模型为

2 供水温度预测模型的设计
当室外温度变化时,二次网供水温度控制系统的输入值也应随之变化,需要采用先进算法得到精确的二次网供水温度设定值。由于供热系统没有精确的数学模型,本文建立了径向基函数(RBF)神经网络预测模型。RBF神经网络相比BP神经网络是一种性能较好的前向神经网络模型,收敛速度快效率高,不存在局部极小化问题[9,10]。
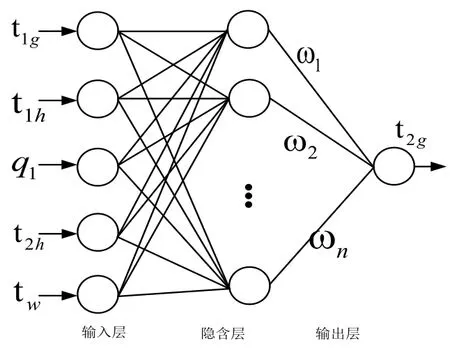
图3 RBF神经网络预测模型结构图Fig.3 Forecasting model structure figure of RBF neural networks
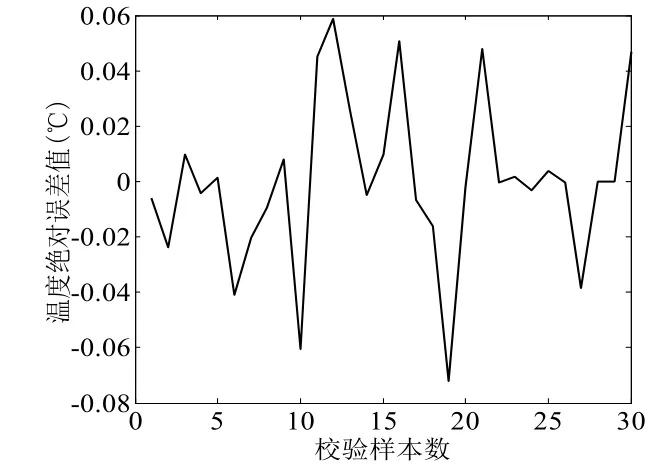
图5 RBF预测模型校验误差图Fig.5 Verification calibration error figure of RBF forecasting model
RBF神经网络由输入层,隐含层和输出层组成,本文采用了影响二次网供水温度的5个因素作为输入量,分别为一次网供水温度t2g、一次网回水温度t2h、一次网流量q1、二次网回水温度t2h以及室外温度tw。隐含层节点数量与非线性映射能力相关,隐含层节点越多,网络的非线性映射能力就越强,反之网络的非线性映射能力就越弱[11]。隐含层节点数量的确定由网络自动调节。输出量为二次网供水温度t2g。图3为RBF神经网络预测模型结构图。
为创建神经预测模型,需要对网络进行训练和校验。实验数据来自天津市静海区某换热站,网络训练所用的198组数据为2016年11月16日至20日现场测得的数据,数据采样间隔时间为10 min。在Matlab中建立并训练RBF神经网络。为了达到理想的预测精度,径向基函数扩展速度进行了调整,预测精度为0.01。通过实验,扩展速度取0.0052。网络校验所用的30组实验数据为2016年11月29日的实测数据。RBF预测模型校验预测图,如图4所示。
如图5所示,网络校验实验中得到二次网供水温度的平均绝对误差为0.0048℃。
供水温度自适应控制器的设计
由于供热系统存在滞后性,为消除其给控制系统带来的不良后果本文引入Smith预估补偿。其原理为:利用人造模型的方法将事先设计好的补偿环节并联在原控制系统中实现将纯延迟的环节转移到控制回路之外从而改善控制效果[12]。
集中供热系统是一个时变非线性系统,若只采用模糊控制不容易达到满意的效果,所以选择模糊PID控制[13]。其原理为:在控制器中输入偏差E和偏差变化率Ec,经模糊化和模糊推理之后再经去模糊化处理得到输出值U,即PID控制器的比例、积分、微分参数,根据模糊控制器的输出值对自身参数进行修正调整,见公式(4)、(5)、(6)。PID控制器时域输出u(t)方程见公式(7)。式中:ΔKp、ΔKi、ΔKd均为通过模糊推理得到参数校正值;Kp0、Ki0、Kd0均为模糊PID参数的初始值。

自适应Smith-Fuzzy-PID控制器的结构见图6。
在供热温度控制系统中,二次网供水温度的变化直接取决于一次网的阀门开度大小,对一次网的阀门开度调节策略至关重要。在整体调节过程中,对阀门开度一共有三种调节方式:定开度调节、定温度调节、温补动态调节。随着供热的运行,控制器会根据温度偏差e的大小,采取三种不同的调节方式,将系统依次划分为三个不同的运行阶段,直至最后供热站稳定运行,供热站运行调节过程如图7。其中e1,e2为设定的偏差范围且满足 0<e1<e2。
由经验知,自适应控制器对反馈量与输入量之间的偏差十分敏感,随着误差增大,其控制精度逐渐下降。为解决这一问题,在主反馈通道中加入一个惯性环节1/(tfs+1)(其中tf为滤波时间常数),作为滤波处理避免偏差的变大[14]。供热过程中,供热系统模型与自适应控制器失配可由放大倍数、时间常数或滞后时间变化引起。当放大倍数改变时,引入惯性环节会降低控制效果且如果放大倍数误差较大,模糊PID控制器也可能失去控制作用,此时自适应机构会根据反馈信号y/ym导数值为零而不引入惯性环节进行滤波;当时间常数和滞后时间发生改变时,自适应机构会根据反馈信号y/ym导数值不为零而引入惯性环节能对系统进行控制。
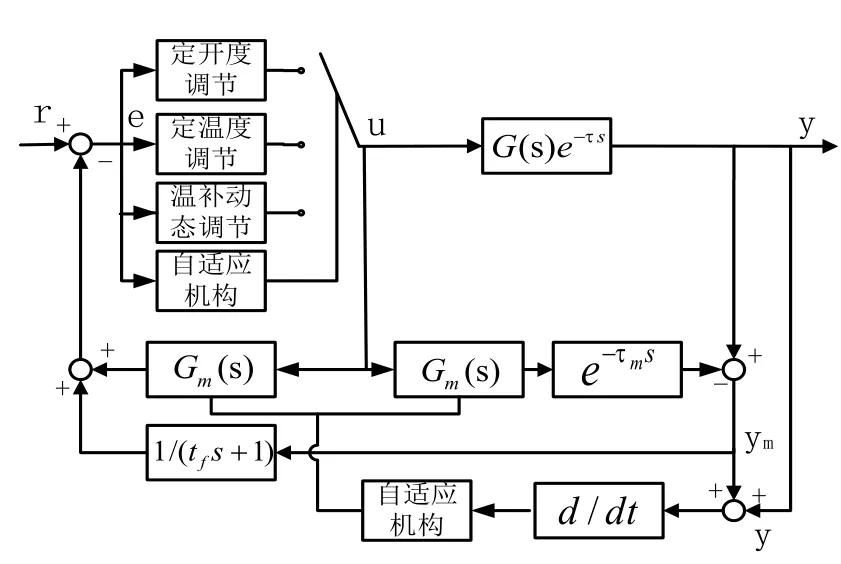
图6 自适应Smith-Fuzzy-PID控制器结构Fig.6 Structure figure of adaptive Smith-Fuzzy-PID controller
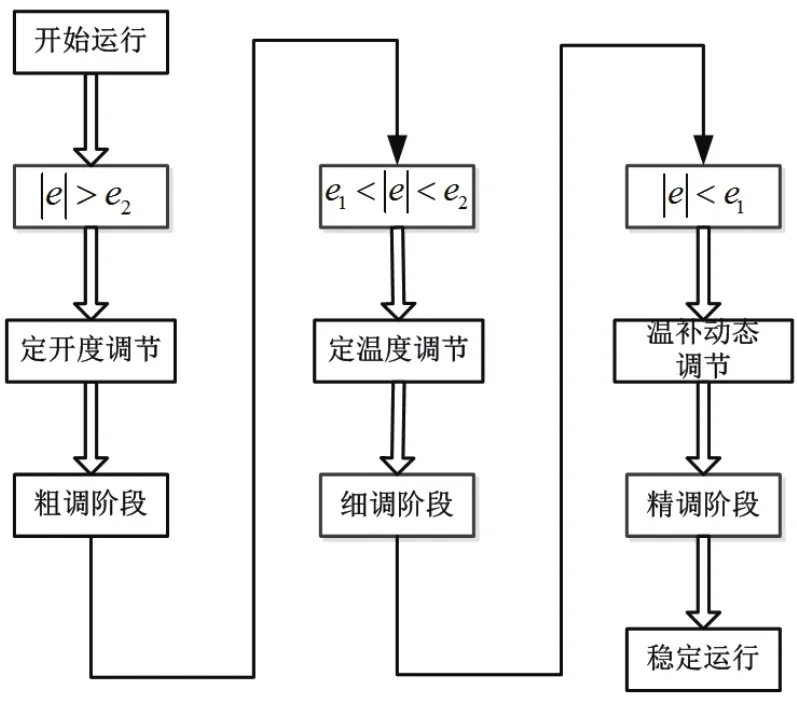
图7 供热站运行调节过程Fig.7 Heating station operation adjusting process
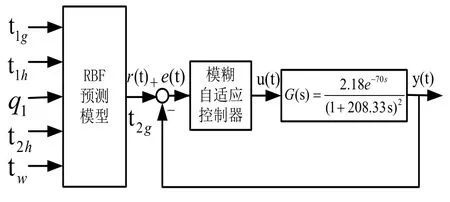
图8 供水温度控制系统框图Fig.8 Control system of supply water temperature
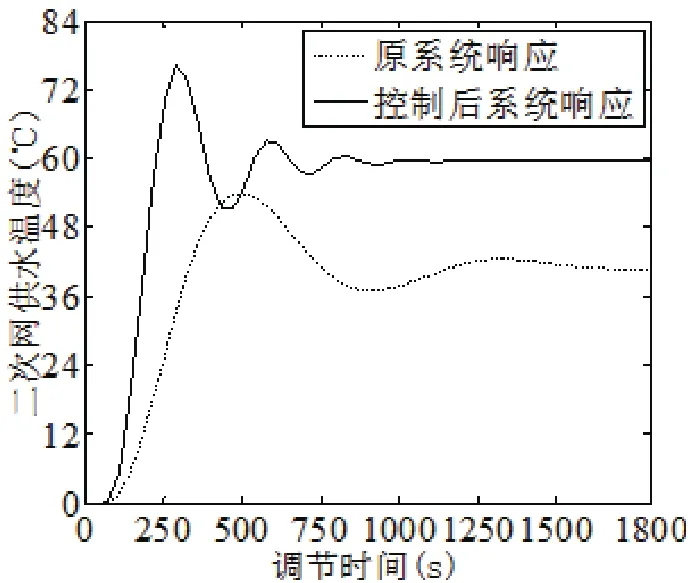
图9 系统控制仿真输出Fig.9 Simulation output of control system
4 供热系统仿真研究
供水温度控制系统为一闭环控制系统,见图8。
RBF预测模型的输入为一组矢量值:一次网供水温度t1g、一次网回水温度t1h、一次网流量q1、二次网回水温度t2h以及室外温度tw,模型输出二次网供水温度t2g作为控制系统的给定值r(t)。控制对象是集中供热二次供水管网温度控制系统的数学模型。控制量y(t)为二次网供水温度。现场采得的15组数据用作RBF预测模型的输入、输出仿真数据见表1,可得预测结果精确有效。
在Matlab中对系统模型建立Simulink仿真实验。各参数设置如下:论域e=ec=u=[-6,+6],量化因子ke、kec分别取 0.1、0.6,比例因子 kp、ki、kd分别取 0.1、0.001、0.02。PID初始参数kp0、ki0、kd0设为3.2、0.001、2。模糊规则参考文献[15]。仿真实验结果如图9、10、11、12所示。
图9、10 分别显示了系统在控制后和受干扰时的阶跃响应,由图9可知,在控制其作用下,系统超调20%, 调整时间为550 s,使供热系统短时间内达到稳定状态。由图10可知,系统在1100 s时受到一个干扰信号影响,由于自适应控制器的调节作用,大约经过200 s的时间重新回到稳定状态。
由经验可知,当室外温度急剧变化时,供热系统的数学模型主要受放大倍数变化的影响;当用户自身调节室内温度时,供热站的负载易发生变化,供热系统的数学模型主要受时间常数变化的影响。供热系统受外界信号扰动时易引起与预定模型不相匹配。
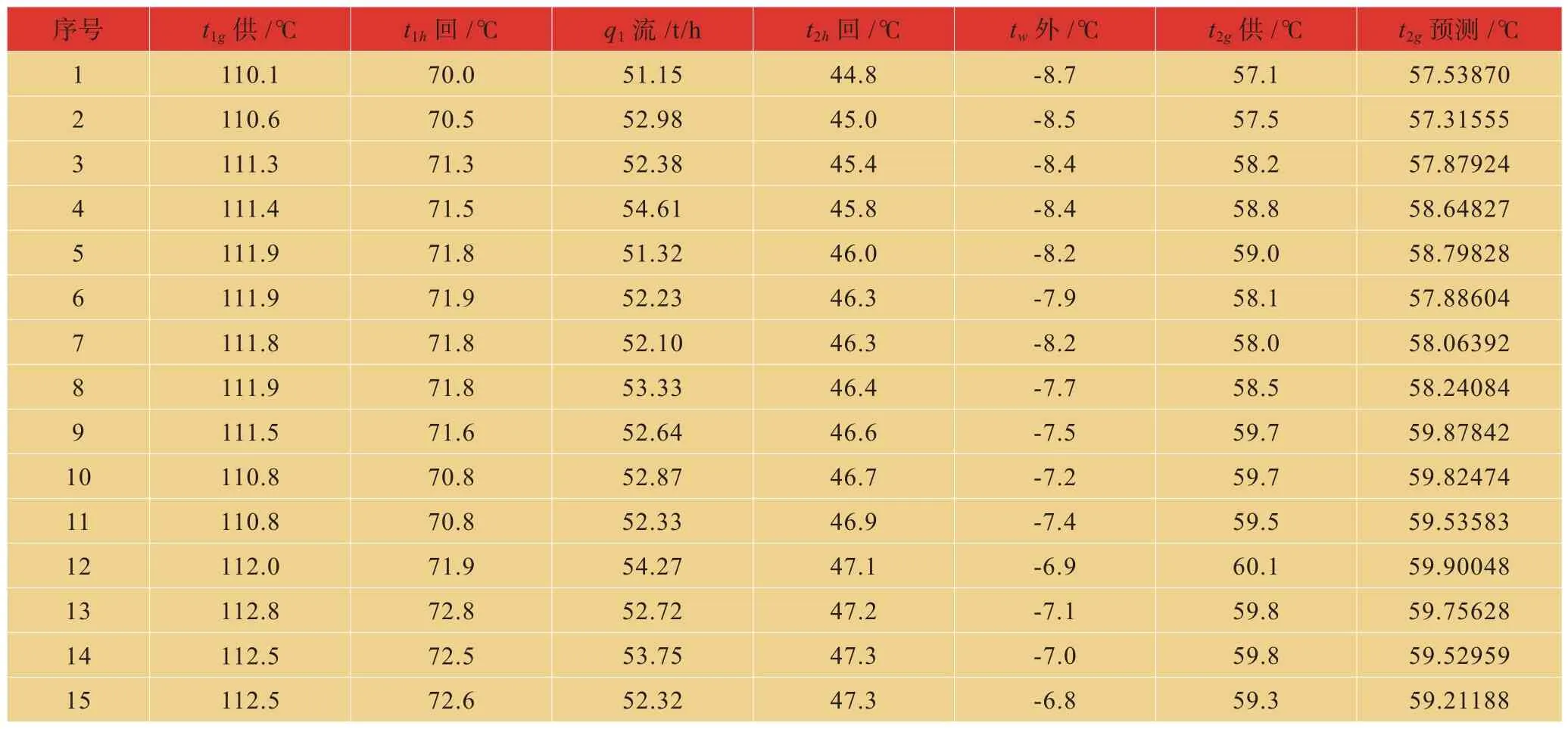
表1 仿真实验数据Table 1 Simulation of experimental data
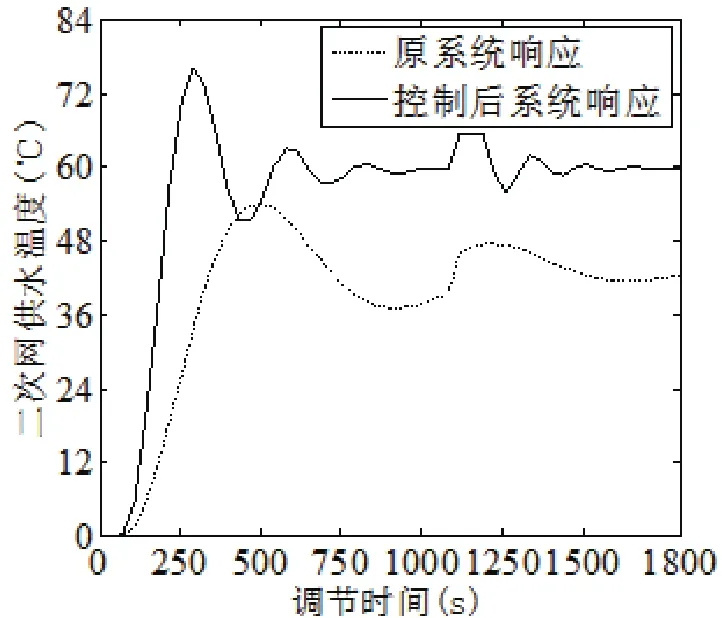
图10 系统受外界干扰时控制仿真输出Fig.10 Simulation output of control system by outside interference
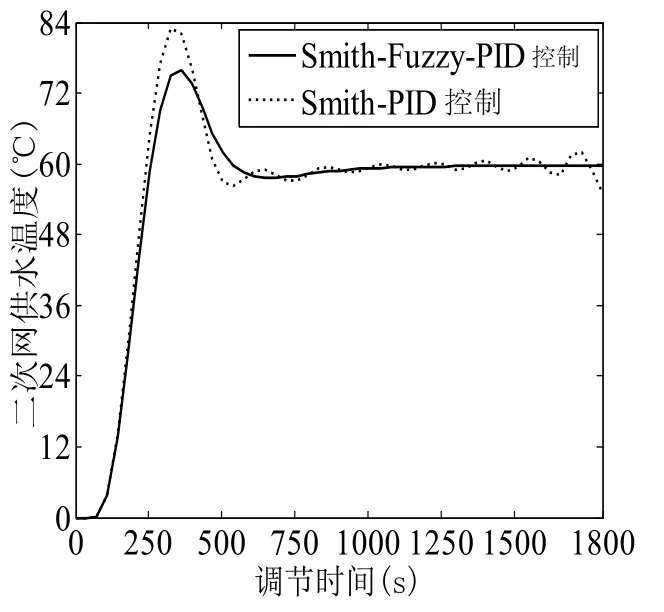
图11 时间常数T增大50%时的仿真Fig.11 Simulation output of the time constant increased by 50%
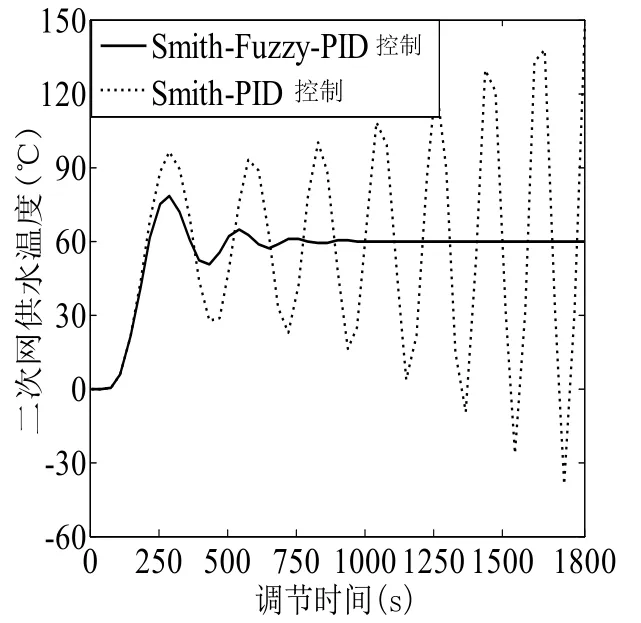
图12 放大倍数A增大50%时的仿真Fig.12 Simulation output of the amplification increased by 50%
下面分别对放大倍数K放大50%和时间常数T增大50%时对二次网供水温度的影响进行仿真,如图11、12。图11中,传统Smith-PID控制超调40%,调整时间600 s;Smith-Fuzzy-PID控制超调20%,调整时间550 s。图12中,Smith-PID控制彻底失去了作用,Smith-Fuzzy-PID控制仍然稳定控制。因此,本文的算法超调小,响应速度快,鲁棒性好,避免了因放大系数、时间常数变化带来的系统不稳定问题。
5 结论
建立的基于RBF神经网络预测模型,预测的平均温度绝对误差为0.0048℃,可精确预测二次网供水温度值;
在自适应Smith-Fuzzy-PID控制算法下,系统超调量为20%,调整时间为550 s,迅速使原系统达到预期的稳定值,而且具有抗干扰能力;
与传统Smith-PID控制相比,自适应Smith-Fuzzy-PID控制超调小,响应速度快,而且可有效解决系统在放大倍数和时间常数变化时的模型失配问题,鲁棒性好。
[1] 陈震,于洋. 供热系统运行调节公式的建立及应用分析[J]. 区域供热,2011,30(01):22-24.Chen Zhen,Yu Yang.Establishment and application analysis of regulating formula of heating system operation[J]. District Heating,2011,30(01):22-24.
[2] 沈志华,赵英凯,张湜. 步进梁加热炉神经网络模型预测控制[J].控制工程,2005,12(S1):87-89.SHEN Zhi-hua, ZHAO Ying-kai, ZHANG Shi. Neural network model predictive control for steel rolled reheating furnaee[J]. Control engineering of China,2005,12(S1):87-89.
[3] 张煜.换热站供热系统研究及智能控制方案设计[D]. 鞍山: 辽宁科技大学,2011.Zhang Y. The study of heat exchange station heating system and the design of intelligent control program [D]. Anshan: University of Science and Technology Liaoning, 2011.
[4] 孙文来. 供热系统模糊PID控制应用研究[D].华北电力大学(河北),2004.SUN Wen-lai. Research on fuzzy PID control of heat supply system[D]. North China Electric Power University,2004.
[5] 张涛.基于模糊控制算法的采煤工作面通风调节模型的设计[J].新型工业化,2014,4(4):39-44.ZHANG Tao.Design of Ventilation Regulation Model at the Coal Mining Working Face Based on Fuzzy Control Algorithm[J].The Journal of New Industrialization,2014,4(4):39-44.
[6] 刘玉霞,熊娟,金升平.基于模糊动态规划算法的船舶航速最优调度模型研究[J].新型工业化,2014,4(1):33-37.LIU Yu-xia,XIONG Juan,JIN Sheng-ping.The Optimal Scheduling Model of Ship Speed Based on The Fuzzy Dynamic Programming Algorithm[J].The Journal of New Industrialization,2014,4(1):33-37.
[7] M S Bass,A G Batukhtin. An Integrated Approach for Optimizing the Operation of Modern Heat Supply Systems[J]. Thermal Engineering,2011,58(8): 678 - 681.
[8] 曾琳,张文涛.基于RBF神经网络的智能PID控制算法[J].计算机与数字工程,2011, 39(1):17-20.Zeng L, Zhang W T. Intelligent PID control based on rbf neural network [J]. Computer & Digital Engineering, 2011, 39(1): 17-20.
[9] 王卫兵,杨传香,王伟,等.改进BP算法解耦热网控制器的设计与仿真[J]. 哈尔滨理工大学学报,2012, 17(02):58-62.WANG Wei-bing,YANG Chuan-xiang,WANG Wei,et al. Design and simulation based on advanced BP algorithm decoupling controller of heat network[J]. Journal of Harbin University of Science and Technology,2012,(02):58-62.
[10] Fernandez de Canete J, Gonzalez-Perez S, Saz-Orozco P del. Software tools for system identification and control using neural networks in process engineering [J]. Engineering and Technology,2008,47(3):59-63.
[11] 朱林,赵晓斌. 基于SOM和RBF网络的软测量方法研究[J].计算机测量与控制,2015,13(04):1112-1114+1117.ZHU Lin,ZHAO Xiao-bin. Research and application of soft measurement method based on SOM and RBF network[J]. Computer Measurement & control, 2015,23(04):1112-1114+1117.
[12] 解英杰,尤洋,谢慕君. Smith-Fuzzy-PID在集中供热控制系统中的应用研究[J]. 计算机测量与控制,2014,12(09):2823-2825.XIE Ying-jie,YOU Yang,XIE Mu-jun. Applications study of Smith-Fuzzy-PID in central heating system[J]. Computer Measurement &control, 2014,(09):2823-2825.
[13] 唐彪.基于模糊PID的Smith预估控制器及应用[D].中南大学,2010.TANG Biao. Smith predictive controller and its application based on fuzzy PID[D]. Central South University,2010.
[14] 安连祥,马华民,刘永刚,等. 基于改进Smith预估器的二阶时滞系统[J]. 计算机仿真,2011,28(01):198-200+233.AN Lian-xiang, MA Hua-min,LIU Yong-gang, et al. A 2th order time delay system based on improved fuzzy Smith predictor [J].Computer Simulation,2011,(01):198-200+233.
[15] 葛楠,李铁鹰,王宇慧. 变论域模糊PID算法在供热控制中的应用[J]. 科学技术与工程,2012,(34):9203-9206.GE Nan,LI Tie-ying,WANG Yu-hui. The application of variable universe fuzzy PID algorithm in heating control system[J]. Science Technology and Engineering,2012,(34):9203-9206.

