基于改进非支配排序遗传算法的维修资源优化配置

王文双，赵建印，赵建忠，张 鑫

（海军航空工程学院a.科研部；b.兵器科学与技术系，山东烟台264001）

基于改进非支配排序遗传算法的维修资源优化配置

王文双a，赵建印b，赵建忠b，张 鑫b

（海军航空工程学院a.科研部；b.兵器科学与技术系，山东烟台264001）

针对在武器装备维修保障过程中出现的资源短缺、资源冲突等问题，构建了多目标的维修资源优化配置模型，并且基于加权思想将多目标转化为单目标以方便求解。针对遗传算法求解多目标优化问题存在的解空间过大、收敛速度慢、计算效率低等问题，提出了基于约束的改进非支配排序遗传算法对资源优化配置模型进行求解。实例分析结果验证了模型及算法的可行性和有效性。

武器装备；维修资源；资源配置；多目标进化算法；非支配排序遗传算法

维修保障资源是武器装备保障系统实施维修任务所必须的物质基础，是开展维修保障活动的基本载体。维修资源种类或数量的短缺均直接影响着维修保障组织的维修能力，从而影响相应维修保障机构上维修任务的顺利实施。武器装备保障中的维修资源配置问题通常涉及多个目标的同时优化，各优化目标间可能不一致甚至互相冲突[1]。进化算法是一类模拟生物自然选择和自然进化的随机搜索算法，具有隐含的并行性和在全局解空间进行搜索的能力。它一次运行便能得到一组折衷解，非常适合求解多目标优化的问题。国内外学者已提出多种典型求解多目标的进化算法（Multi-Objective Evolutionary Algorithm，MOGA）[2-8]。其中，非支配排序遗传算法NSGA-II既有良好的分布性又有较快的收敛速度，已被广泛应用。本文构建了维修保障资源优化配置模型，将多目标函数通过加权转换为单目标函数，并在NSGA-II算法的基础上，结合优化配置模型的优化目标和约束条件，提出一种基于约束的改进NSGA-II算法。

1 维修资源优化配置模型的构建

1.1 资源、组织及任务的约束关系

记在某个维修保障过程中所有资源种类集合为R={Ri,i=1,2,…,I}，参与实施维修任务的维修保障组织为V={Vi,i=1,2,…,N}。在维修保障过程中，每类维修保障资源均可能隶属于维修保障组织中的一个或多个机构，且每个机构上所配置的数量不同。通过对每个维修机构上所配置的资源类型及对应数量的统计，构建维修保障组织与资源对应的关联矩阵，简称为组织-资源约束关系矩阵为[9]：

式（1）中，RVji代表在维修保障机构Vj上所配置资源Ri的数量。

由式（1）中的列元素，可得出每类资源在每个维修机构上配置的数量，通过行元素的统计可得到每个维修保障组织上所配备的每类资源的数量。

在维修保障过程中，通过维修任务调度可得到维修任务与维修机构之间的分配关系。对每个维修机构上所分配的维修任务按照执行顺序依次编号，记某一维修保障机构Vj上经调度后的维修任务集合为MVj={MVjh,h=1,2,…,H} ，对每个维修任务MVjh对应所需的每类维修保障资源进行统计，构建维修机构Vj上所分配维修任务及其资源需求对应的任务-资源需求约束关系矩阵为：

式（2）中，RMjhi表示Vj上执行的第h个维修任务所需要资源Ri的数量。

由式（2）中每行非零元素即可知每个维修任务执行过程中资源需求的类型及相应的数量，由每列非零元素即可得到该列资源需求所对应的维修任务。

1.2 优化配置模型的建立

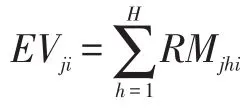
由式（1）可得到维修保障机构SVj上所配置资源Ri的数量RVji，满足EVji＞RVji，即SVj需要向其他配备资源Ri的组织进行支援请求以解决资源短缺问题。记所有维修保障机构的资源支援集合S={Sji,j=1,2,…,J;i=1,2,…,I}，其中Sji表示机构SVj需要资源Ri的支援。记Sji对应所需的资源数量为SRji，满足：

通过搜索式（1）中资源Ri对应列中的非零元素，可得到配置资源Ri的维修保障机构节点集合。选取其中能够满足SRji的维修保障机构集合Vji={Vk,Vk∈V,k=1,2,…,N且k≠j}，记其中Vk上资源Ri可用数量为RVk*i，Vk上所配置资源Ri的数量为RVki，满足

根据式（1）、（2）中的资源配置与资源需求约束模型及式（4）所示的Sji对应所需的资源数量为SRji，结合这3个约束条件得出满足式（5），即能够对Sji提供支援的支援组织约束矩阵：

式（6）中，xjik表示机构Vk能否向维修保障机构SVj支援资源Ri的判断值，满足：

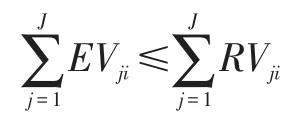
对于资源静态优化配置模型的目标主要考虑以下两方面的目标函数[10-12]：

1）使得每个需要支援的维修保障机构SVj上资源等待时间最短；

资源配置方案Π下的判断矩阵Y表示为：

式（8）中，W表示资源支援集合S中集合元素的总数。

在配置方案Π中，由Vk向维修保障机构SVj提供资源Ri的支援时，yjik=1；否则，yjik=0。

由此，可建立资源静态优化配置模型为：

式（15）表示每个维修保障机构上所提供某种资源支援的数量不能超过本身所配置的数量。

1.3 基于多目标加权的模型转换

由于每个维修保障机构资源配置的数量、运输能力有限及不同维修保障机构间的差异等问题，很难使得每个机构上等待资源的时间达到最小。因此，决策者必须依据一定的偏好准则，使得T(Πj)取得其相应的极小值。借鉴文献[7]中的维修点优先级概念，依据维修保障机构的优先级确定相应的等级权重，将多个维修保障机构的资源等待时间最小的多目标转换为加权的单目标。假定维修保障机构SVj的优先级为αj，根据维修保障机构的优先级确定一个权重系数λj，得出相应的等级权重：

维修保障机构SVj的优先级αj与机构的重要度βj与资源需求率δj等有关。其中，SVj的重要度βj由维修任务的紧迫性、时效性、故障的可维修性及规定时间内维修任务的完成率等指标共同加权决定。资源需求率δj满足：

根据文献[13]中的计算方法，通过对βj与δj运用理想点方法得出每个维修保障机构Vj的优先级αj，然后通过式（10）得到相应的等级权重Wj，从而将式（9）中的目标函数转换为：

2 基于CINSGA-II求解算法的设计

非支配排序遗传算法（NSGA-II）在基本遗传算法的基础上，通过运用快速非支配排序法降低了计算复杂性，提出精英策略防止优秀解的丢失，并通过引入分布函数保持种群多样性[14-18]。

本文在采用NSGA-II算法的基础上，结合资源配置的决策目标与支援组织约束矩阵对算法进行约束化，提出一种基于约束的改进NSGA-II算法（CINSGA-II，Constrained and Improved NSGA-II），对其主要进行以下改进：①依据维修保障机构优先级、时间排序及资源约束等条件的限定设定偏好系数，基于偏好系统生成初始种群，提升算法的导向性；②对染色体编码与解码操作进行配置决策及组织支援的约束化，简化遗传编码与遗传算子的设计，提升算法的搜索与计算效率；③依据组织约束矩阵对染色体的交叉、变异范围及方式进行设计，从而去掉无意义的解、缩小解的空间，减少早熟收敛的概率并改善收敛速度。

根据NSGA-II算法的基本流程，CINSGA-II算法在对资源静态优化配置模型进行求解过程中，主要考虑初始种群的生成、编码、解码、选择操作、交叉操作与变异操作等关键问题，具体算法流程如图1所示。

2.1基于偏好系数产生初始种群

遗传算法对初始种群的依赖性使得初始解的质量对算法求解的效果产生较大的影响。通常，应用NSGA-II算法时初始解是随机产生的，由此使得种群进化方向不够明确。本文提出的算法在产生初始种群时，根据维修保障机构的优先级，对每个维修保障机构资源需求配置的排序进行初步约束。同时，通过搜索式（6）Sji对应行中的非零元素，得出Sji的支援组织集合Vji，对集合中元素分别依据预期支援时间及所需成本从小到大进行排序，然后设定一个偏好概率系数πji，如果随机产生的随机值小于πji则选择支援时间较小的支援机构，否则选择成本较小的支援机构。

2.2 基于决策目标与约束模型的编码与解码

在资源静态优化配置中，配置的决策目标包括资源需求的配置顺序与支援资源需求的维修保障机构选择两方面，在此采用基于配置顺序与机构选择的两层编码。其中，第一层编码采用表示资源需求的配置顺序的自然数编码，基因值为配置顺序随机数，如所有维修保障机构一共有10个资源，则基因为所产生的1～10之间不同的随机数；第二层表示向第一层资源需求提供支援的支援机构编号，通过搜索式（6）所示约束模型中Sji对应行中非零值，得到Oji。如Oji中包括V1与V2，则依据偏好概率系统随机选择1或2作为Sji对应的第二层编码基因值，如表1所示为一条染色体的编码示例。

表1 两层染色体编码示例Tab.1 Sample of two-layer coding example

表1中，由第一层编码中顺序编号可知，维修保障机构资源需求的配置序列为(S14,S11,S42,S44,S22,S13,S31,S21,S33,S23)，由第二层编码可得到V1上先后支援资源需求序列为(S44,S23)，V2上的序列为（S14，S33），V3上的序列为(S42,S22,S13)，V4上的序列为(S11,S31,S21)。

假设基层级维修保障机构（级别值为3）的运输能力为1（每次只能运输1种资源），中继级维修保障机构（级别值为2）的运输能力为2（可以连续运输2种资源），基地级维修保障机构（级别值为1）的运输能力为3（可以连续运输3种资源）。在进行解码时需根据支援资源需求Sjik的Vk对应级别及Vk所提供资源支援的数量来计算支援资源到达的时间为Tjik。以Vk为中继级维修保障机构为例，当其处理的资源需求序列为(Sj′i′,Sj″i″,Sji)时，记Sj′i′,Sj″i″,Sji的运输起始时间分别为T′j′i′k,T′j″i″k,T′jik，运输时间分别为运输到达时间分别为Tj′i′k，Tj″i″k，Tjik。由此，Tj′i′k、Tj″i″k的计算式为：

资源需求Sji所需资源到达时间Tjik的计算式为：

即T′jik为前2个资源到达后再返回总时间的最小值。当Vk为基层级与基地级维修保障机构时，Tjik的计算由其所处支援维修保障机构上的顺序及其之前资源需求的运输时间所决定，计算方法与式（19）、（20）类似。

依据上述方法进行解码后，可得到每个支援维修保障机构上的资源需求先后顺序、每个资源需求到达时间；然后，将解码结果用于计算拥挤度与目标函数值。

2.3 Pareto快速非支配排序与拥挤距离计算

Pareto非支配排序的目标是将种群中所有个体依据非支配解设定相应的等级。在构建非支配解时，运用文献[19-20]中所定义的进化个体间的关系：对于∀q1,q2∈P0，如果q1＞q2（q1支配q2）且q1、q2相不相关，则有q1＞dq2。在进行快速排序过程中，选择一个个体q1为基准对象，将种群中其他个体分别依据关系“＞d”进行比较，由此将种群分为以q1为界的2个部分。然后对这2个部分以同样的方法依次进行快速排序，直至完成所有个体的排序，由此形成非支配曲面集F={Fi,i=1,2,…,i0}，Fi表示处于第i个非支配等级的非支配曲面。

拥挤距离是维持群体分布多样性的重要参数，针对种群中某一层非支配个体qi，记其拥挤距离为L[qi]d，则计算式为：

式（21）中：qi为非支配排序后的第i个个体；qi+1与qi-1为其相邻排序的2个个体；r为目标总维数，在资源静态优化配置模型中，r=2；k代表第k个目标维。

2.4 选择操作

通过拥挤距离的计算，可以确保算法收敛到一个均匀分布的Pareto曲面。通过快速排序与拥挤距离的计算，相应得到每个个体qi的非支配排序等级与拥挤距离级L[qi]d。

在进行择优选择时为确保种群的多样性及收敛到较优的Pareto曲面，本文通过引入一个限制父代精英解的分布函数：

式（22）中：Ni为Fi上选取个体的数目；|Fi|为第i个非支配等级曲面上个体总数；ri为[0 ,1]间的随机数。

种群中分别处于l1与l2个非支配等级上的2个个体，如果l1＜l2，则优先选择；如果l1=l2且L[ql1]d＞L[ql2]d，同样优先选择ql1，选择数量通过式（21）所决定，否则优先选择ql2。

2.5 交叉操作

鉴于资源配置中的两层编码及编码间的对应关系，在进行交叉操作时需一一对应。对于配置顺序所对应的第一层编码，采用线性次序交叉法，随机选取若干个交叉位置或交叉片段，将2个位置上的基因或基因片段进行互换，然后在原父代个体中删除所交叉过来的基因，然后将剩下的基因依次填入未交叉的位置。对于选择组织对应的第二层编码，由于式（6）所示的支援组织约束，每个资源需求对应可选的维修保障机构是限定的，因此交叉操作需要在2个个体对应的位置进行。首先随机选取若干个基因位置或基因片段位置，将2个个体中所选取位置上对应的基因进行交叉，其他位置的基因复制到子代相应的位置。两层编码的交叉操作示例如图2所示。

2.6 变异操作

针对第一层顺序编码，在此采用转换变异法，即随机交换个体中若干个基因的位置。对于第二层组织选择编码，采用多位置替换变异法，即针对某个位置对应资源需求，通过搜索得到式（6）中的行向量中非零元素集Oji，随机选取集合中的其他元素进行替换。如图3所示，对第一层编码变异操作中，交换位置4与7之间的基因；对第二层编码变异操作中，对第3和7个位置上的基因进行替换。其中，第3与7个位置上可替换元素集分别为{1，2，4}与{2，3，4}。

2.7 终止条件

为改变以往遗传算法在规定最大进化代数的终止条件下，无法收敛到最优解或已收敛到最优解后仍继续搜索的问题，在此采用的终止条件为：在指定的迭代次数中，如果子代精英种群的Pareto最优解与父代最优解差值比在规定范围内，则说明算法已收敛到Pareto最优解，迭代终止。

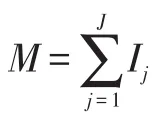
3 案例分析

以某型舰载武器装备为例，针对其在一个为期60 d的训练周期内的使用与维修情况进行分析，对该段时间内维修任务执行过程中出现冲突与短缺的设备与备件的优化配置进行分析。选取出现冲突与短缺的设备与备件种类作为重点分析对象，同时基于现行的维修保障体制，在此主要考虑舰员级、中继级、基地级三级维修机构。记分析起始时刻为t=0，此时所考虑的设备、备件及对应维修机构上相应的配备情况即组织-资源约束数据如表2所示。

表2 组织-资源约束数据Tab.2 Organization-resource constraint data

依据各级维修机构上所分配维修任务对于上述各类设备与备件需求的统计，得到表3所示的组织-资源需求约束。

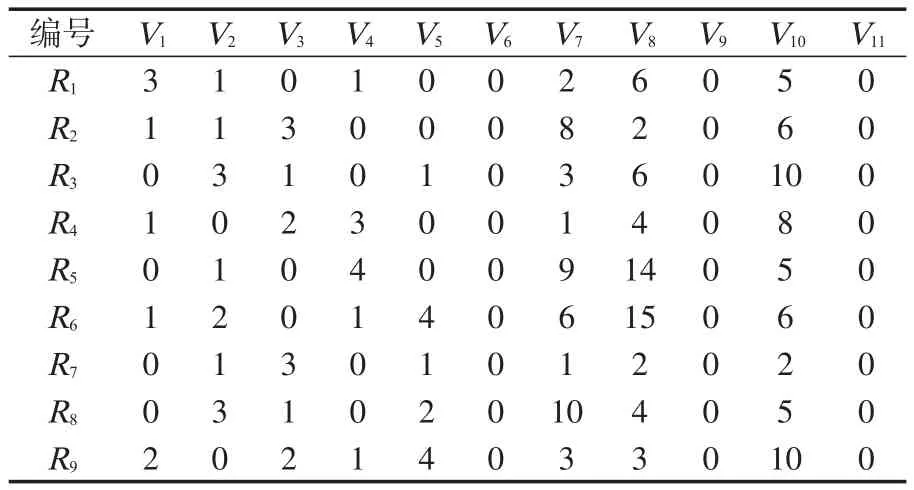
表3 组织-资源需求约束数据Tab.3 Organization-resource requirement constraint data

由表1与2所示的组织-资源约束及组织-资源需求约束，由此可得到所有组织资源支援集合为：

依据表1与2，通过式（4）与（5）的求解，得到支援组织约束矩阵为：

根据该型装备的维修保障系统设计要求、维修保障机构设置及分布，每个维修保障机构向支援组织进行申请相应所需的设备与备件运输时间（h）与所需成本（万元）的估计值可分别表示矩阵T与C。

经计算需要支援的维修保障机构{V1,V2,V3,V4,V5,V7,V8}的 等 级 权 重 值 分 别 为 ：{0.204,0.182,0.158,0.147,0.115,0.103,0.091}。令资源配置开始执行时刻t=0，初始化各维修保障机构资源配置起始时间为0。运行参数设置为：种群大小为100，交叉概率为0.45，变异概率为0.25，选择概率为0.85，最优前端个体系数为0.2，终止条件的差值比为0.001。在算法运行过程中，自动绘制第一前端中个体分布。以某次运行过程为例，算法迭代停止后，得图4所示的第一前端个体分布图，即Pareto最优解分布图。

从图4中可看出，第一前端的Pareto最优解分布均匀，说明算法取得了较好的搜索效果。算法运行结束后，Workspace中返回最优解对应的目标函数值如表4所示。

表4 Pareto最优解对应的目标函数值Tab.4 Objective function values corresponding to the Pareto optimal solutions

由表4求得2个目标函数的均值分别为fˉ1=4.009，fˉ2=1.047。综合资源等待时间及总成本，选取第10个Pareto最优解作为案例资源优化配置模型的最优解，最优解对应的资源优化配置方案的甘特图如图5所示。

为验证本文模型及算法的有效性，使用传统的资源配置策略对案例中的资源需求进行资源配置，记为方案1。传统的资源配置策略即不考虑同级维修机构间资源共享，在出现资源短缺时，直接向本级仓库申请资源，如本级仓库库存不足，则逐级向上级进行资源申请。同时，分别运用NSGA-II算法与本文算法对案例对应的资源优化配置模型进行求解，记为方案2与方案3。运用2种算法独立计算10次，计算目标函数的均值，并对算法的平均运行时间进行统计。3种方案所得的目标函数值分别如表5所示。

表5 3种方案的目标函数值Tab.5 Objective function values of the three plans

由表5可见，方案3对应的目标函数值均优于方案1与方案2。其中，方案3相对于方案1的资源等待时间平均值减小了37.67%，总成本减小了47.41%，说明相对于传统资源配置策略，本文所构建的资源优化调度模型能够有效地优化资源配置策略，在维修任务执行过程中出现资源短缺时以较短的时间与较低的成本满足各类资源需求。依据方案3与方案2的目标函数值对比可知，本文所提出的CINSGA-II算法的求解效果优于基本的NSGA-II算法。同时，由2种算法在同一台计算机上的平均运行时间对比可知，本文算法在计算效率上高于NSGA-II算法。说明通过对NSGA-II算法的改进及约束化，在有效地实现对资源优化配置模型求解的同时，达到了缩小解的搜索空间与降低计算复杂度的效果。

4 结束语

武器装备维修保障资源优化配置能够大大缩短待修装备的平均等待时间，在较短的时间内恢复装备的战斗力，最大限度提高维修保障系统效能。本文针对在武器装备维修任务实施过程中出现的配置不足、资源冲突等资源短缺问题，构建了维修资源配置以最短等待时间、最小成本为目标函数的多目标资源优化配置模型，并且在对多目标优化配置模型求解方法对比分析的基础上，结合武器装备维修保障资源配置的约束模型，提出了基于约束的改进NSGA-II算法对资源优化配置模型进行求解，极大地缩小了解空间，提高了算法的搜索与求解效率。后续可以研究维修资源随维修任务、维修保障组织、保障资源变化的动态优化配置建模问题。

[1]朱亚红，曹继平，王正元，等.变精度粗糙集的战时装备维修保障资源优化配置[J].火力与指挥控制，2014，39（6）：40-44. ZHU YAHONG，CAO JIPING，WANG ZHENGYUAN，et al.Optimal deployment of equipment maintenance support resources based on variable precision rough set in wartime[J].Fire Control&Command Control，2014，39（6）：40-44.（in Chinese）

[2]黄晶晶，郑龙席，刘钢旗.基于第二代非支配排序遗传算法的转子优化设计[J].推进技术，2015，36（12）：1881-1886. HUANG JINGJING，ZHENG LONGXI，LIU GANGQI. Design and optimization of a two-disk Rotor[J].Journalof Propulsion Technology，2015，36（12）：1881-1886.（in Chinese）

[3]杨慧娜，刘钢.基于二代非支配排序遗传算法的电子变压器多目标优化[J].华北电力大学学报，2013，40（5）：31-35. YANG HUINA，LIU GANG.Optimization design of highpower electronic transformer based on NASG-Ⅱ[J].Journal of North China Electric Power University，2013，40（5）：31-35.（in Chinese）

[4]WANG H，LIU Y.Multi-objective optimization of power system reconstruction based on NSGA-Ⅱ[J].Automation of Electric Power Systems，2009，33（23）：14-18.

[5]DEB K，PRATAP A，AGARWAL S.A fast and elitist multi-objective genetic algorithms：NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197．

[6]陈青艳，胡成龙，焦红卫.多工序车削的自适应搜索非支配排序遗传算法[J].机械设计与制造，2013（7）：119-122. CHEN QINGYAN，HU CHENGLONG，JIAO HONGWEI.Adaptive search non-dominated sorting genetic algorithm of multi-pass turning operations[J].Machinery Design＆Manufacture，2013（7）：119-122.（in Chinese）

[7]刘爱军，杨育，程文明.复杂制造环境下的改进非支配排序遗传算法[J].计算机集成制造系统，2014，39（6）：2446-2458. LIU AIJUN，YANG YU，CHENG WENMING.Improved NSGA for complex manufacturing environment[J].Computer Integrated Manufacturing Systems，2014，39（6）：2446-2458.（in Chinese）

[8]王丽美，蔡剑锋，钟一文.基于非支配排序遗传算法Ⅱ的双聚类优化研究[J].大理学院学报，2014，13（12）：15-21. WANG LIMEI，CAI JIANFENG，ZHONG YIWEN.Optimization biclustering algorithm based on parallel nondominated sorting genetic algorithmⅡ[J].Journal of Dali University，2014，13（12）：15-21.（in Chinese）

[9]夏良华，龚传信.装备保障资源柔性分配研究[J].装备指挥技术学院学报，2004，15（3）：30-32. XIA LIANGHUA，GONG CHUANXIN.Research of flexible assignment for equipment support resource[J].Journal of the Academy of Equipment Command&Technology，2004，15（3）：30-32.（in Chinese）

[10]张洪涛，崔珊珊，刘广.机群保障资源配置建模与优化研究[J].系统工程理论与实践，2015，35（4）：1019-1026. ZHANG HONGTAO，CUI SHANSHAN，LIU GUANG. Resource scheduling for air fleet oprerations[J].Systems Engineering-Theory＆ Practice，2015，35（4）：1019-1026.（in Chinese）

[11]SUMAN B，KUMAR P.A survey of simulated annealing as a tool for single and multi-objective optimization[J]. Journal of the Operational Research Society，2006，57（10）：1143-1160．

[12]DIVINA F，AGUILAR，RUIZ J S.A multi-objective approach to discovery biclusters in microarray data[C]//Proceedings of the 9thAnnual Conference on Genetic and Evolutionary Computation.2007：385-392.

[13]曹继平，宋建社，郭军，等.一种战时装备维修保障资源优化调度算法[J].系统仿真学报，2007，19（15）：3390-3394. CAO JIPING，SONG JIANSHE，GUO JUN，et al.Optimization dispatching arithmetic of equipment maintenance support resources in wartime[J].Journal of System Simulation，2007，19（15）：3390-3394.（in Chinese）

[14]张超勇，董星，王晓娟.基于改进非支配排序遗传算法的多目标柔性作业车间调度[J].系统仿真学报，2007，19（15）：3390-3394. ZHANG CHAOYONG，DONG XING，WANG XIAOJUAN.Improved NSGA-II for the multi-objective flexible job-shop Scheduling Problem[J].Journal of System Simulation，2007，19（15）：3390-3394.（in Chinese）

[15]DEB K，PARTAP A，AGARWAL S，et al.A fast and elitist multi-objective genetic algorithm：NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.

[16]韩毅，于恩林，许学文.基于非支配排序遗传算法的直缝焊管焊接工艺参数优化[J].燕山大学学报，2015，39（5）：403-407. HAN YI，YU ENLIN，XU XUEWEN.Optimization of longitudinal welding parameters based on non-dominated sorting genetic algorithm[J].Journal of Yanshan University，2015，39（5）：403-407.（in Chinese）

[17]KALYANMOY DEB，AMRIT PRATAP，SAMEER AGARWA.A fast and elitist multiobjective genetic algorithm：NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197．[18]刘士明，于丹.基于第二代非支配排序遗传算法（NSGA-Ⅱ）的水资源优化配置[J].水资源与水工程学报，2013，24（5）：185-188. LIU SHIMING，YU DAN.Optimal allocation of water resources based on non-dominated sorting genetic algorithm-Ⅱ[J].Journal of Water Resources&Water Engineering，2013，24（5）：185-188.（in Chinese）

[19]郑金华.多目标进化算法及其应用[M].北京：科学出版社，2007：167-213. ZHENG JINHUA.Multi-objective evolutionary algorithm and application[M].Beijing：Science Press，2007：167-213.（in Chinese）

[20]RAQUEL C，NAVAL P J.An effective use of crowding distance in multi-objective particle swarm optimization [C]//Proceedings of the 2005 Conference on Genetic and Evolutionary Computation.2005：257-264.

Optimal Configuration of Maintenance Resource Configuration Based on Improved Non-Dominated Sorting Genetic Algorithm

WANG Wenshuanga,ZHAO Jianyinb,ZHAO Jianzhongb,ZHANG Xinb
（Naval Aeronautical and Astronautical University a.Department of Scientific Research; b.Department of Ordnance Science and Technology,Yantai Shandong 264001,China）

Aiming at the problems of resource conflict,shortage,resource requirement and available resource diversifica⁃tion in the maintenance support process,the multi-objective optimization models of resource static and dynamic configura⁃tion were built.To address the disadvantages of genetic algorithm,such as the large solution domain,slower convergence speed,and low computing efficiency,the constraint-based improved non-dominated sorting genetic algorithm(CINSGA-I) was raised.The example analysis results validated the effectiveness and superiority of the model and algorithm.

weapon equipment;maintenance resource;resource configuration;multi-objective evolutionary algorithm; non-dominated sorting genetic algorithm

E919；TP315

：A

1673-1522（2017）01-0121-08

10.7682/j.issn.1673-1522.2017.01.005

2016-10-08；

：2016-12-07

王文双（1977-），男，助理研究员，硕士。