一种基于非线性回归的载人航天器密封舱内在轨噪声分析方法

李 喆，柏林厚，李兴乾，张 昊，曲 溪，于泓淼

（中国空间技术研究院 载人航天总体部，北京 100094）

一种基于非线性回归的载人航天器密封舱内在轨噪声分析方法

李 喆，柏林厚，李兴乾，张 昊，曲 溪，于泓淼

（中国空间技术研究院 载人航天总体部，北京 100094）

文章提出一种载人航天器密封舱内噪声非线性回归通用分析方法，可基于地面噪声试验测得的数量较多的数据样本和在轨噪声测试获取的少量数据样本，建立密封舱内位置-在轨噪声的数学模型。经验证该模型能够较为准确地拟合密封舱内在轨噪声水平，从而为开展载人航天器的降噪设计、优化噪声仿真模型和验证降噪措施效果提供数据支持。

载人航天器; 密封舱；在轨噪声；非线性回归分析

0 引言

载人航天器长期载人飞行中，密封舱内噪声是极为重要的环境因素。噪声会影响航天员工作效率，危害航天员的身心健康，因此需对舱内噪声进行严格的评价及控制。经识别，载人航天器密封舱内噪声的主要来源为风机、泵和控制力矩陀螺，其中风机噪声为辐射传播，泵和陀螺的噪声为振动传导[1-2]。

美国和俄罗斯均对国际空间站舱内噪声开展了深入研究，获得了较为丰富的在轨噪声数据，并形成一套有效的降噪措施[3-7]。随着我国长期飞行载人航天器研制工作的开展，针对舱内噪声的研究也取得了一系列的成果，如提出了噪声控制的具体措施，并在地面实施了模拟在轨飞行状态的噪声测试，验证了噪声控制设计与仿真结果的一致性等。由于我国长期飞行载人航天器上开展的噪声测量试验较少，在轨噪声数据稀缺，所以当前的研究多为地面研制阶段开展的预先设计和验证[1,8-10]。

本文提出了一种基于非线性回归的载人航天器密封舱内噪声通用分析方法，以某载人航天器地面阶段测得的密封舱内人主要活动区域的噪声数据样本为基础，建立了位置-噪声地面非线性回归模型，再结合在轨阶段测得的少量噪声数据样本，进一步建立了在轨噪声与地面噪声的非线性回归模型，最终获得了位置-在轨噪声的非线性回归模型。利用该模型可较为科学地拟合舱内人主要活动区域的在轨噪声水平，从而为地面开展降噪措施的有效性分析、修正降噪设计方案和优化噪声仿真模型提供数据支持。

1 噪声测量数据说明

1.1 地面噪声测量数据

地面研制阶段在某载人航天器上开展了密封舱内噪声测量试验[1]。如图1所示，航天器水平放置在架车上，I象限朝地，设置为航天员驻留期间的工作模式，前舱门关闭。使用声强计对舱内噪声进行测量，声强计衰减模式设置为A计权模式。

将声强计探头从d剖面开始，沿d到a剖面的方向在距脚踏板1600 mm高处纵向轴线每隔固定距离测量1次噪声，共测得19个位置的噪声值，每个位置偏差不超过±50 mm。

测得位置-噪声记录值见表1（表中数据进行了归一化处理，下同）。其中，位置的起始点定义为0.1，步长为0.05，噪声基值为19个测量位置实测噪声的最大值。

表1 地面噪声测量数据记录（归一化处理后）Table 1 Ground noise measurement data(normalized)

绘制地面测量的位置-噪声数据散点图（图2）。

1.2 在轨噪声测量数据

根据声强计在轨布局安排，测得4个点的噪声值见表2。位置起点、步长均与地面噪声测量相同，噪声数据归一化处理的基值仍为地面噪声测量试验中19个测量位置实测噪声的最大值。

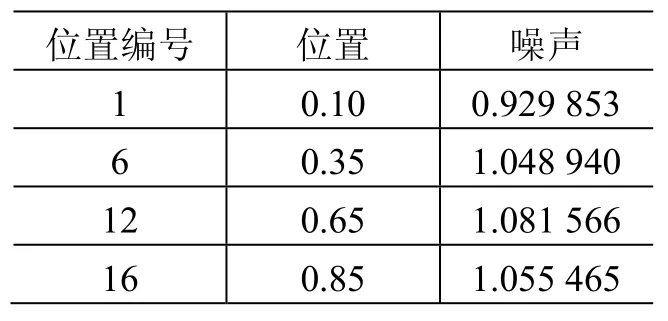
表2 在轨噪声测量数据记录（归一化处理后）Table 2 On-orbit noise measurement data

绘制在轨测量的位置-噪声数据散点图（图3）。

1.3 测量数据对比分析

对比发现，在同样的测量位置，在轨噪声比地面噪声大，这是由于地面阶段载人航天器放置于水平架车上，泵和陀螺振动时能量可部分传导至大地，而在轨无此传播途径。

2 舱内噪声回归分析

2.1 地面噪声回归分析

设地面阶段舱内噪声为因变量y，位置为自变量x，通过图2可判断，位置-噪声是一种非线性关系。工程上采用回归方法进行数据分析时，可通过变量替换将非线性关系转化为线性关系进行处理[11-13]。

利用多项式回归模型，则回归方程可表示为

从而将多项式模型转换为多元线性回归模型，应用线性回归的方法进行参数估计。

地面噪声随机变量y与一般位置变量x1,x2, …,xp的多元线性回归模型为

其中：b0,b1,b2, …,bp为不依赖x1,x2, …,xp的未知参数，b0称为回归常数，b1,b2, …,bp称为回归系数；ε是随机误差项。

这里对x1,x2, …,xp和y进行n次观测，得到n组观测值xi1,xi2, …,xip和yi，i=1, 2, …,n，它们满足关系式

X是一n×(p+1)矩阵。

为了方便模型的参数估计，对方程有如下基本假定：

1）变量xi1,xi2, …,xip是确定性变量，X是一满秩矩阵；

2）随机误差项具有零均值和等方差，即满足Gauss-Markov条件E(εi)=0，i=1, 2, …,n，

3）随机误差项服从正态分布ε～N(0,σ2In)。

由样本数据得到回归参数的估计值，最常用的方法是最小二乘估计。采用最小二乘法即寻找参数b0,b1,b2, …,bp的估计值，当(XTX)-1存在时，即得回归参数的最小二乘估计为

位置-噪声的多元线性回归模型需要检验多个自变量与因变量之间是否存在相应的线性关系。如果多元线性的显著性检验结果为不显著，则说明因变量与自变量不存在明显的线性关系，无法采用多元线性回归进行拟合。因此，显著性是采用多元线性进行噪声拟合的前提和基础，常用的显著性检验方法有R检验、T检验和F检验3种。

2.2 地面-在轨噪声回归分析

以在轨噪声为因变量yorbit，设g=yorbit-y代表在轨噪声与地面噪声的差值。假定g与位置x同样为多项式回归模型，则回归方程可表示为

令x1=x,x2=x2, …,xq=xq，得到

将多项式模型转换为多元线性回归模型，应用线性回归的方法进行参数估计。

2.3 在轨噪声数学模型

由式(2)和式(8)可以得出

从而建立了在轨噪声数学模型，进而实现对舱内噪声的拟合。

3 仿真结果

3.1 地面噪声模型仿真结果

应用SPSS分析软件，建立表1中地面测量位置-噪声数据的线性、对数、反向、二次、三次、复合、幂、S、增长、指数非线性回归模型，绘制拟合曲线见图4。

计算上述10种数学模型的R2检验值，见表3。

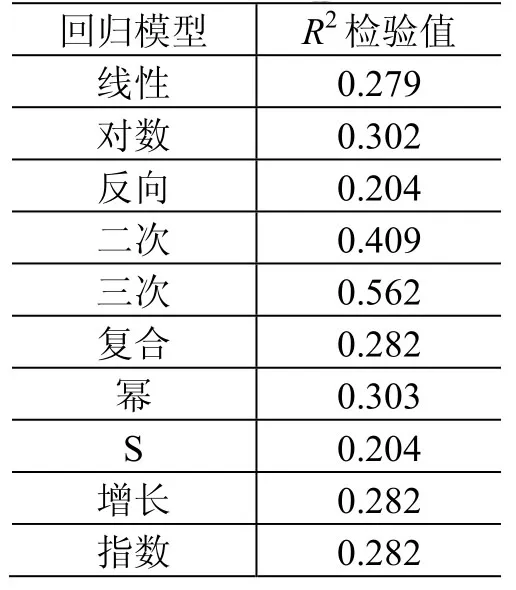
表3 地面噪声数学模型R2检验值Table 3 Mathematical model of ground noise test value (R2)

由表3可见，三次多项式的R2最大，拟合度最优，但仍远小于1，表明样本回归线对样本观测值的拟合程度仍然较差。选择扩大因变量范围，以x,x2,x3,x4,x5,x6,x7,x8,x9,x10作为自变量，进行多元线性回归分析。在递归过程中，发现x4,x5,x7,x8,x9,x10在进行检验时对y的影响不显著，排除它们，保留x,x2,x3,x6，得到回归模型为y=1.022-0.681x+ 2.067x2-1.773x3+0.343x6。经计算，R2检验值为0.866，相比三次多项式的R2检验值0.562更接近于1，显著性明显提高；F检验值为10.510，大于临界值2.36；回归参数T检验值如表4所示。

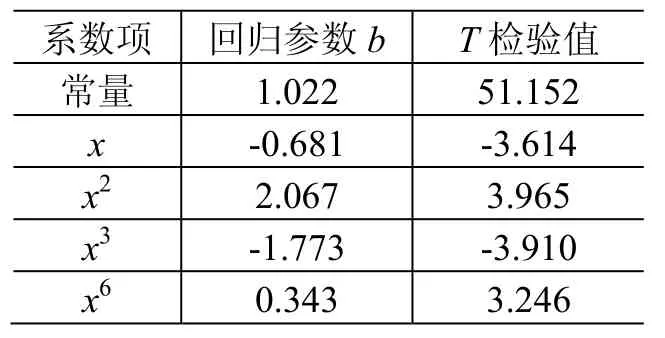
表4 地面噪声数学模型回归参数T检验值Table 4 Mathematical model of ground noise test value (T)

对模型的适合性进行检验，主要是对残差进行分析。图5所示为模型残差散点图，可以看出各散点随机分布在以0为中心的横带中，证明了该模型的适合性。

绘制残差的正态概率图和直方图（图6），从图中可以直观地判断出残差符合正态分布。

绘制模型对地面实测噪声值的拟合图（图7）。

3.2 地面-在轨噪声模型仿真结果

通过表1和表2计算得出在轨噪声与地面噪声差值的样本数据，见表5。

表5 在轨-地面噪声差值与位置观测样本值Table 5 The difference betweenon orbit and ground noise vs the observation position

这里留出x=0.35点作为后续使用的检验点，以x=0.10、0.65和0.85点作为数据样本，同样应用SPSS统计软件建立在轨-地面噪声差值g与位置x的线性、对数、反向、二次、三次的非线性回归模型，绘制拟合曲线如图8所示。由于因变量g包含负数，所以无法计算复合、幂、S 、增长、指数模型。

计算上述5种数学模型的R2检验值，见表6。

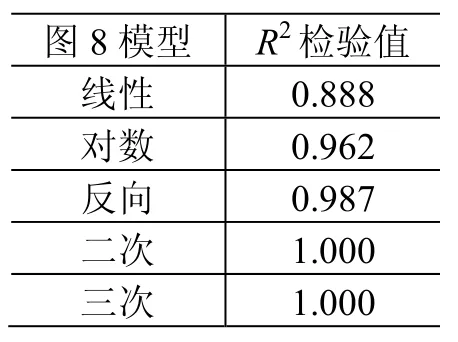
表6 在轨-地面噪声差值与位置非线性模型R2检验值Table 6R2test values of the non-linear model of the difference between the noises on ground and on orbit and position

由表6可见，二次和三次多项式模型的R2值约为1，可实现对样本的完全拟合。从模型简化的角度，选取二次多项式方程，为

同样地，分别以x=0.35、0.65和0.85点作为数据样本，以x=0.10、0.35、0.85点为数据样本，以x=0.10、0.35、0.65点作为数据样本，得到g-x二次多项式方程为：

3.3 在轨噪声模型计算结果

结合位置-地面噪声数学模型，可得位置-在轨噪声的数学模型为：

分别将x=0.10、0.35、0.65、0.85代入到上面4个模型中，计算出模型拟合值与实际在轨测量值间的偏差分别为16.46%、3.72%、4.39%、10.26%。通过对比可发现，以样本点为0.10、0.65、0.85计算所得的方程经验算后偏差最小，拟合度最高。因此，位置-在轨噪声的数学模型选定为方程(15)。

用选定的在轨噪声模型绘制位置-噪声关系拟合图（图9）。

4 结束语

采用非线性回归分析方法对某载人航天器密封舱内噪声数据进行了分析，推导得出该密封舱内位置-在轨噪声关系的数学模型。通过模型验证，实测在轨噪声值与模型计算值偏差控制在 4%以内，表明模型准确度较高，可对地面降噪设计和噪声仿真提供数据支持，并可为重要在轨活动开展期间航天员主动避噪提供指导。

（References）

[1]魏传锋, 张伟, 曹剑峰, 等.载人航天器密封舱噪声控制与试验[J].航天器环境工程, 2013, 30(1): 91-93 WEI C F, ZHANG W, CAO J F, et al.Noise control and test in sealed cabin of manned spacecraft[J]. Spacecraft Environment Engineering, 2013, 30(1): 91-93

[2]张帆, 杨江, 冯咬齐, 等.空间站舱内噪声评价与降噪技术现状及建议[J].航天器环境工程, 2014, 31(2): 223-227 ZHANG F, YANG J, FENG Y Q, et al.Current state of art and suggestions about noise evaluation and control for the space station[J].Spacecraft Environment Engineering, 2014, 31(2): 223-227

[3]GROSVELD F W, GOODMAN J R, PILKINTON G D.International Space Station acoustic noise control-case studies[C]//Proceedings of Noise Conference 2003.Washington DC: US Institute of Noise Control Engineering, 2003

[4]GOODMAN J R, GROSVELD F W.Acoustics in habitable space vehicles and enclosures[C]//Proceedings of 3rdIAASS Conference.Rome, 2008

[5]GOODMAN J R.International Space Station acoustics[C]//Proceedings of Noise Conference 2003.Washington DC: US Institute of Noise Control Engineering, 2003

[6]O’KEEFE E , COUNTER D.On-orbit noise control for Space Station Freedom[C]// AIAA Space Programs and Technologies Conference and Exhibit.Huntsville, AL, 1993-09.DOI: 10.2514/6.1993-4080

[7]ALLEN C S, DENHAM S A.International Space Station acoustics: a status report: NASA-2010- 0039608[R]

[8]金岩.载人航天器热控分系统噪声控制[J].航天器环境工程, 2012, 29(5): 571-573 JIN Y.The noise control technology in thermal control subsystem of manned spacecraft[J]. Spacecraft Environment Engineering, 2012, 29(5): 571-573

[9]耿丽艳, 李新明.载人飞船泄复压过程中轨道舱的噪声环境试验研究[J].航天器环境工程, 2008, 25(6): 568-570 GENG L Y, LI X M.The acoustic environment in the orbit cabin during the depressurization & repressurization courses[J].Spacecraft Environment Engineering, 2008, 25(6): 568-570

[10]武登云, 李刚, 鲁明.1000 N·m·s控制力矩陀螺噪声测试与分析[J].空间控制技术与应用, 2012, 38(6): 31-34 WU D Y, LI G, LU M.Noise test and analysis of 1000 N·m·s control moment gyroscope[J].Aerospace Control and Application, 2012, 38(6): 31-34

[11]李春燕, 俞集辉, 谢开贵.基于多元非线性回归的阻塞管理优化模型[J].电工技术学报, 2008, 23(2): 96-102 LI C Y, YU J H, XIE K G.Optimal model of congestion management based on non-linear regression[J].Transactions of China Electrotechnical Society, 2008, 23(2): 96-102

[12]周晓华, 张树人, 唐斌, 等.环保型多重掺杂 X7R瓷料的多元非线性回归分析[J].无机材料学报, 2006, 21(3): 683-688 ZHOU X H, ZHANG S R, TANG B, et al.Multiple non-linear regression analysis for complex doping of X7R MLCC ceramics[J].Journal of Inorganic Materials, 2006, 21(3): 683-688

[13]宋向荣, 刘芳, 钟秋海, 等.基于遗传规划的中厚板轧制力矩的非线性回归[J].北京理工大学学报, 2006, 26(12): 1077-1080 SONG X R, LIU F, ZHONG Q H, et al.Non-linear regression of rolling torque for medium and heavy plate based on genetic programming[J].Transactions of Beijing Institute of Technology, 2006, 26(12): 1077-1080

（编辑：张艳艳）

A analysis method of on-orbit noise in manned spacecraft pressurized cabin based on non-linear regression

LI Zhe, BAI Linhou, LI Xingqian, ZHANG Hao, QU Xi, YU Hongmiao
(Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China)

The noise inside a manned spacecraft pressurized cabin in orbit is an important issue for astronauts.In this paper, a non-linear regression analysis method for the noise in the manned spacecraft pressurized cabin is proposed.From the noise data of a manned spacecraft pressurized cabin, the on-orbit position-noise math model is built by this method.It is shown that the noise deviation between the value calculated by the on-orbit math model and the value measured by test is less than 4%.The model could offer predicted on-orbit noise data for the noise reduction design, the noise simulation and the noise reduction measure verification on the ground stage.

manned spacecraft; pressurized cabin; on-orbit noise; nonlinear regression analysis

V476.1

：A

：1673-1379(2017)01-0063-07

10.3969/j.issn.1673-1379.2017.01.010

李 喆（1983—），男，硕士学位，从事载人航天器总体设计工作。E-mail: lzxoyo@163.com。

2016-07-10；

：2017-01-19

国家重大科技专项工程

李喆,柏林厚,李兴乾,等.一种基于非线性回归的载人航天器密封舱内在轨噪声分析方法[J].航天器环境工程, 2017, 34(1): 63-69

LI Z, BAI L H, LI X Q, et al.A analysis method of on-orbit noise in manned spacecraft pressurized cabin based on non-linear regression[J].Spacecraft Environment Engineering, 2017, 34(1): 63-69