螺栓预紧力下的应力分析

孙晓萌，麦云飞

(上海理工大学 机械工程学院，上海 200093)

螺栓预紧力下的应力分析

孙晓萌，麦云飞

(上海理工大学 机械工程学院，上海 200093)

针对联接件中螺栓预紧力产生的应力分布情况，利用Hypermesh建立实体螺栓有限元模型，通过建立预紧力截面施加预紧力，利用Abaqus求解得到仿真结果。仿真结果表明，由预紧力生成的应力分布在螺栓附近，其余部分基本不产生应力，且应力最大值出现在螺栓与联接板接触区；同时分析了联接板结合面上的应力分布。

有限元分析；螺栓预紧力；结合面；应力分布

为了便于机器的制造、安装、运输、维修及提高劳动生产率等，各种联接得以广泛的使用。机械结构中应用广泛的联接方式是受拉紧螺栓联接。使联接在承受工作载荷之前，提前受到力的作用。这个预加作用力称为预紧力[1]。

螺栓预紧力就是在拧螺栓过程中拧紧力矩作用下的螺栓与被联接件之间产生的沿螺栓轴心线方向的预紧力。螺栓联接的可靠性、防松能力和螺栓的疲劳强度可通过预紧来提高，且还可增强联接的紧密性和刚性。大量的试验和使用经验证明：较高的预紧力对联接的可靠性和被联接的寿命都是有益的，尤其对有密封要求的联接更为必要，但过大的预紧力会使联接结构失效。因此，预紧力的大小在螺栓联接极为重要。对于有螺栓联接的机械结构进行有限元分析时，如何模拟螺栓联接以及如何将预紧力施加于模型上，较好地模拟螺栓受力情况达到在有限元分析中的准确加载并得到正确的分析结果，有一定难度[2]。本文利用截面法施加螺栓预紧力，分析螺栓联接的应力情况。

1 有限元简介

有限元分析是用比较简单的问题代替复杂问题后再进行求解。其将求解域看成是由诸多称为有限元的小的互连子域组成，每一单元均会有一个合适的假定的(较简单的)近似解，然后推导求解这个域总的满足条件，从而推导出问题的解[3]。因并不是实际的问题，所以该解不是准确解，而是近似解。由于大多数实际问题难以得到准确解，而有限元具有高计算精度高，能适应各种复杂形状，因而成为最常使用且最方便的工程分析手段。有限元方法与其他求解边值问题近似方法的根本区别在于其的近似性仅限于相对小的子域中。

对于不同物理性质和数学模型的问题，有限元分析的基本步骤是相同的，只是具体的公式推导和运算求解不同。有限元求解问题的基本步骤通常为：(1)问题及求解域定义：根据实际问题近似确定求解域的物理性质和几何区域；(2)求解域离散化：将求解域近似为具有不同大小和形状且彼此相连的有限个单元组成的离散域，通常称之为有限元网格划分；(3)确定状态变量及控制方法：将表示具体的物理问题并包含问题状态变量边界条件的微分方程化为等价的泛函形式；(4)单元推导：选择合理的单元坐标系，建立单元试函数，以某种方法给出单元各状态变量的离散关系，从而形成单元矩阵；(5)总装求解：将单元总装形成离散域的总矩阵方程(联合方程组)；(6)联立方程组求解和结果解释：联立方程组的求解可用直接法、选代法和随机法。求解结果是单元结点处状态变量的近似值[4]。

简言之，有限元分析可分成3个阶段：前处理、处理和后处理。前处理是建立有限元模型，完成单元网格划分；后处理则是采集处理分析结果，使用户能简便提取信息，了解计算结果。

2 螺栓预紧力的计算

预紧力Qp的数值应根据载荷性质、联接刚度等条件确定[5-6]。在使用中所施加的预紧力是由旋紧螺帽所施加的扭矩T给出，T可使用测力扳手在旋紧螺帽时测出。拧紧力矩T等于螺旋副间的摩擦阻力矩T1和螺母环形端面与被联接件(或垫圈)支承面间的摩擦阻力矩T2之和，即

T=T1+T2

(1)

螺栓副间的摩擦力矩为

(2)

螺母与支乘面间的摩擦力矩为

(3)

将式(2)和式(3)代入式(1)得

(4)

对于M10～M64粗牙普通螺纹的钢制螺栓，螺纹升角ψ=1°42′～3°2′；螺纹中径d2≈0.9d；螺旋副的当量摩擦角φv=arctan1.155f(f为摩擦系数，无润滑时f≈0.1～0.2)；螺栓孔直径d0≈1.1d；螺母环形支承面的外径D0≈1.5d；螺母与支承面间的摩擦系数fc=0.15。将上述各参数代入式(4)整理后可得

T=0.2Qpd

(5)

因此螺栓预紧力为

(6)

3 螺栓实体有限元建模

3.1 螺栓模拟方式

参考现有的研究文献[7～8]，在有限元分析中常采用7种方式模拟螺栓结构：无螺栓模拟、耦合螺栓模拟、刚体单元螺栓模拟、采蜘蛛网螺栓模拟、混合螺栓模拟、实体螺栓模拟、弹簧单元模拟螺栓结合部等效动力学模型。本文需要考虑螺栓及其联接件的受力特性，研究螺栓的应力分布情况，所以本文采用实体螺栓模拟比较合适。且实体模型模拟螺栓是最贴近现实的仿真方法。其可传递拉伸、弯曲和热载荷[9]。实体螺栓模型需要在上下联接板水平接触面、螺栓头和螺母与法兰的接触上建立接触单元。实体螺栓模型为了简化的需要，忽略了螺纹[10-11]。本文利用Hypermesh建立实体螺栓联接有限元模型，将螺栓与螺母假设为是整体，如图1所示。模型中螺栓头及螺母与联接板建立面—面接触，摩擦系数设为0.18，上下联接板之间同样建立面—面接触，摩擦系数设为0.2，螺杆与联接板之间建立tie接触。

图1 螺栓联接有限元模型

3.2 预紧力施加

创建螺栓预紧力时，可选择下列方法之一：(1)施加力在螺栓上。该方法创建紧固螺栓来承受指定载荷；(2)调整螺栓长度。该方法创建紧固螺栓直到其自由长度由指定值改变；(3)固定螺栓的当前长度。该方法仅当已经在第一个分析步中创建了螺栓而且当前正在随后的分析步中编辑它才可用。该方法允许螺栓长度保持不变以使螺栓中的力根据模型的响应来改变[12-13]。

将预紧力施加在螺栓上时，可利用截面法模拟螺栓预紧力。该方法是在螺杆内部建立一个预紧力截面，在螺帽下部建立一个参考节点，预紧力截面与参考节点之间建立pretension section接触，将预紧力加到参考节点上，如图2所示。

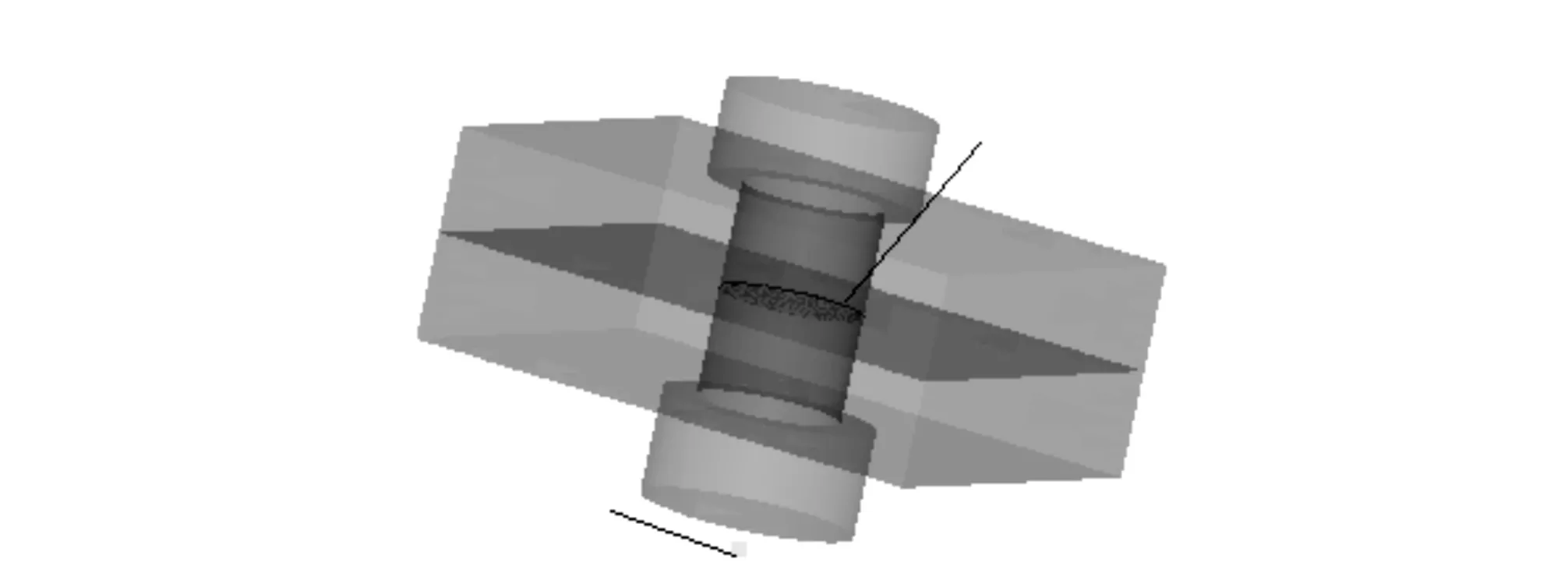
图2 预紧力pretension section

4 螺栓联接实例

以M20螺栓为例，螺杆l=30 mm，直径d=20 mm，螺帽直径30 mm，高13 mm，预紧力矩T=160 N·m，弹性模量E=2.1×105MPa，泊松比μ=0.3。联接板厚度为15 mm，长80 mm，宽60 mm，螺栓材料为45钢，联接板材料为普通钢。计算得到预紧力Qp=40 000 N，预紧力Qp引起的螺杆拉应力为

4.1 预紧力 下仿真结果

通过仿真得到的接触区螺栓径向应力云图和螺栓轴向应力云图如下。

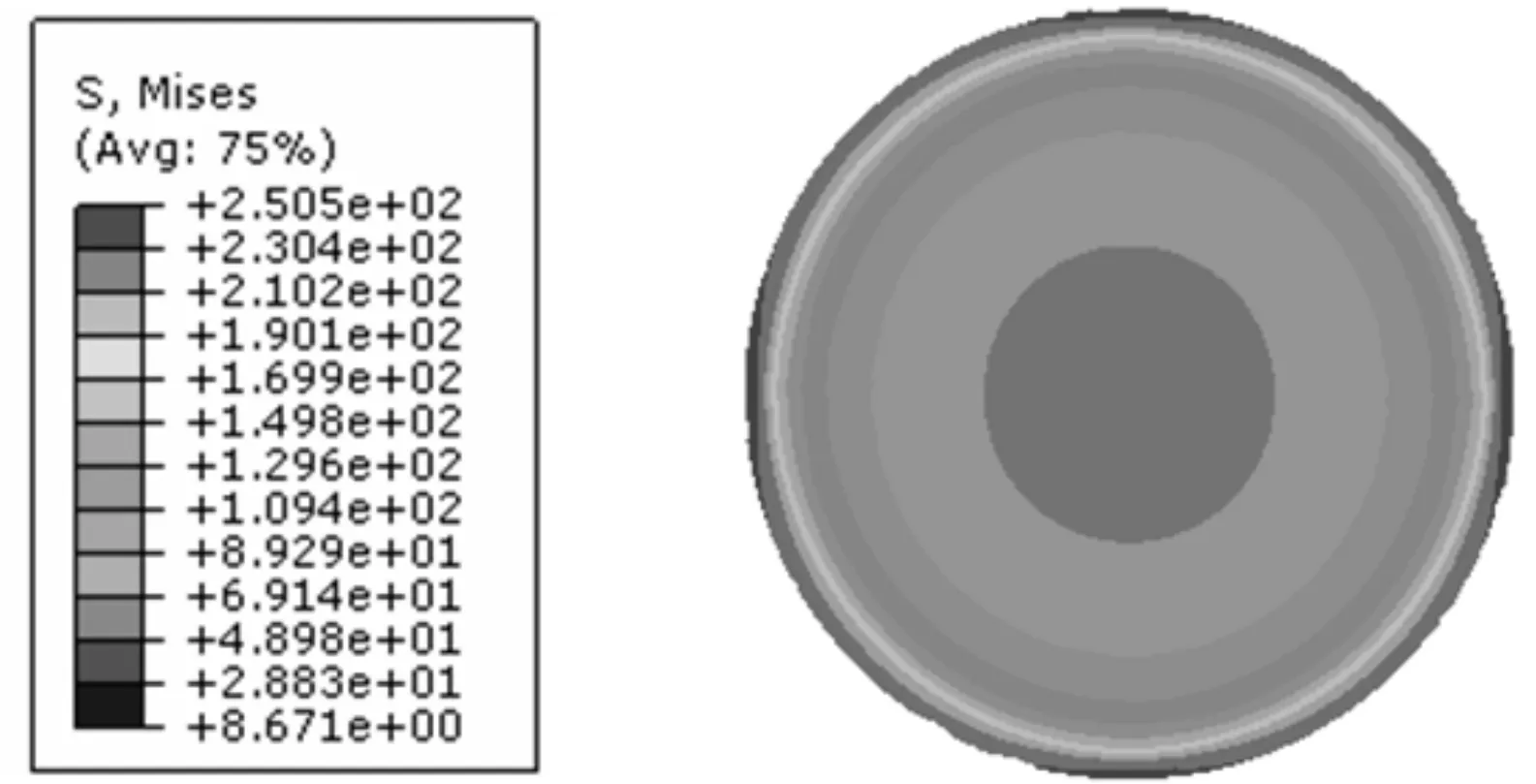
图3 接触区螺栓径向应力云图

图4 螺栓轴向应力云图

提取螺栓截面各节点的轴向应力值并做平均处理[14]，得到轴向平均应力为118.6 MPa，与理论值近似，所以截面法对螺栓预紧力进行仿真可行。上图中可看出，螺杆内部应力分布较均匀，但靠近螺杆接触面区域，应力分布不均与，远离轴心位置应力变大。最大应力出现在螺栓与联接板接触的地方。

4.2 不同预紧力仿真结果

不同的螺栓预紧力会产生不同的应力情况，且对联接板结合面上的影响有所不同[15]。本文施加40 kN和50 kN的螺栓预紧力研究不同螺栓预紧力下应力的分布，两者仿真结果如下图所示。

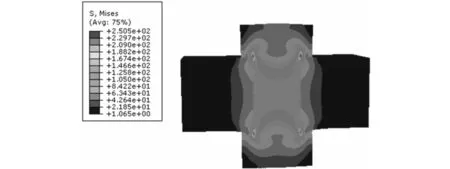
图5 预紧力40 kN下联接板内部应力云图

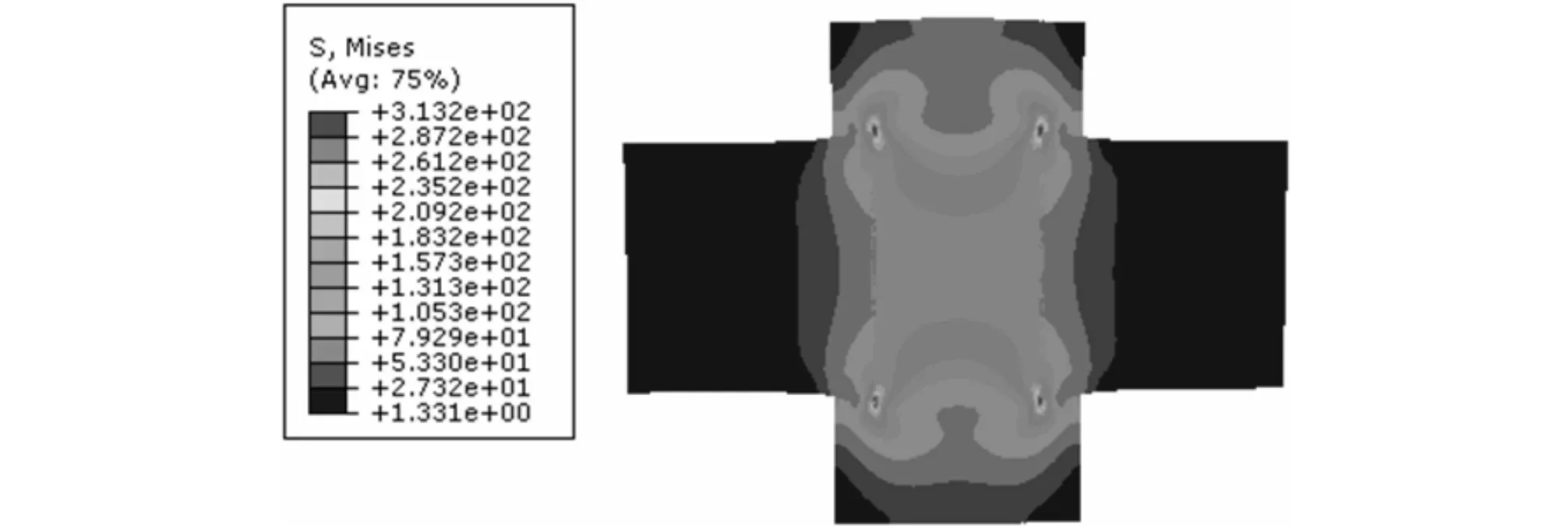
图6 预紧力50 kN下联接板内部应力云图

由图5和图6可看出，不同的预紧力下，应力的分布情况大致相同，应力分布基本维持在在螺栓附近，且最大应力都发生在螺头与联接板接触的地方以及螺栓与螺母联接处。 40 kN预紧力下最大应力值为250.5 MPa，50 kN预紧力下最大应力值为313.2 MPa。

不同预紧力下结合面上的应力分布如图7和图8所示，应力集中分布在靠近螺栓附近，远离螺栓的地方应力较小，且越靠近轴心位置应力越大。不同预紧力下，结合面应力不同，结合面的面压有所不同，所以说较高的预紧力会产生较大的应力，对联接的可靠性和被联接的寿命均是有益的，特别对有密封要求的联接更为必要，但过大的预紧力产生过大的应力会使联接结构失效。因此，控制预紧力在螺栓联接极为重要。

图7 预紧力40 kN下结合面应力云图

图8 预紧力50 kN下结合面应力云

5 结束语

本文研究了预紧力对螺栓联接应力情况的影响。实体螺栓有限元模型理论结果与仿真结果误差约为7%左右，所以有限元模型、接触的定义以及预紧力的施加方法有实际意义，可利用截面法分析预紧力的影响。从仿真结果中可看出，不同螺栓预紧力下，应力的分布情况相同，应力分布在螺栓附近，对其余部分影响较小，且最大应力出现在螺栓与联接板接触的地方。结合面的密封性也受螺栓预紧力的影响，研究结合面密封性时应该考虑预紧力的不同造成的密封性能好坏。

[1] 濮良贵,纪名刚.机械设计[M].8版.北京:清华大学出版社,2006.

[2] 王富生,岳珠峰,张红运.基于三维模型的复合材料层合板单钉螺栓连接件力学性能分析[J].航空制造技术,2010(4):79-82.

[3] 张波,盛和太.ANSYS有限元数值分析原理与工程应用[M].北京:清华大学出版社,2005.

[4] 余娟,余明友,金建伟,等.螺栓连接中预紧力的有限元分析[J].软件导刊,2013(9):64-66.

[5] 李志忠,赵振宇.齿轮箱螺栓结合面的有限元建模研究[J].机电工程,2014,31(6):734-739.

[6] 李会勋,胡迎春,张建中.利用ANSYS模拟螺栓预紧力的研究[J].山东科技大学学报:自然科学版,2006,25(1):57-59.

[7] Montgomery J.Methods for modeling bolts in the bolted joint[C].2002 ANSYS World Users Conference,2002:2-15.

[8] Montgomery J. Modeling multi- bolted systems[C].Toronto,CA:2002 ANSYS World Users Conference，2002.

Analysis of Stress under Bolt Pretension

SUN Xiaomeng，MAI Yunfei

(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

We establish a solid bolt finite element model by using Hypermesh in order to understand the stress of bolt connection, and obtain the simulation results by exerting Pre tightening force on pretension section and using ABAQUS for solution. The simulation results show that the stress generated by the pre-tightening force is near to the bolt with little stress generated elsewhere; the maximum value of stress appears in the contact area between bolt and connecting plate. The distribution of stress on the interface of the connecting plate is analyzed.

finite element analysis; bolt preload; binding surface; stress distribution

2016- 04- 12

孙晓萌(1990-)，女，硕士研究生。研究方向：螺栓联接及结合面密封性的有限元分析。

10.16180/j.cnki.issn1007-7820.2017.02.017

TP391.77

A

1007-7820(2017)02-065-04