边标志算法中常见问题及解决方法
摘 要
本文针对传统的边标志算法在遇到水平边、狭长条以及极值点等情况时会出现错误填充的现象,提出了一种新的改进方法。改进后的算法需要设置一个计量型变量label,访问到一个像素点时将该像素点的label值加1,以完全区别边界点与内点。实验结果表明,改进后的算法对上述问题仅使用标记值加1的简单操作便能够有效的处理,使得改进之后的算法在图形图像数据处理以及多媒体通信等范围内取得更加广泛的适用基础。
【关键词】边标志算法 计算机图形学 扫描转换 区域填充
1 引言
多边形填充是计算机图形学中最基本的算法之一,而边标志算法是多边形填充算法中一种非常简单容易描述的算法。在扫描的过程中设置一个布尔变量Label表示当前点的状态,其初始值为假,对于每一个扫描范围内的像素点如果是多边形边界上的点,便将Label的值取反,当Label的值为真时,便将当前像素点填充为填充色。
边标志算法的这种思想是基于如矩形、椭圆等理想化规则图形才能正确无误的实现。但是在实际应用中,由于计算机硬件设备的限制以及现实生活中各种图形的特点,该算法在离实际应用还有一定的距离。本文在深刻理解现有的边标志算法的基础上,对算法在实现过程中可能出现的问题进行分析,并给出一种相对简单的解决方法。
2 算法的缺陷
2.1 极值点问题
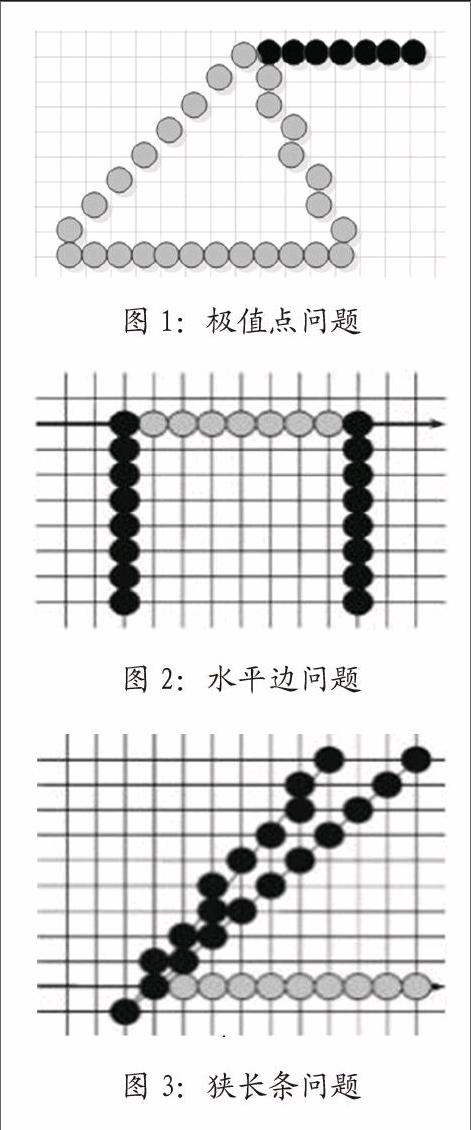
多边形的顶点同时属于两条边,但是并不是所有的顶点都会出现错误填充的现象。如果顶点不属于极值点,则填充正常;否则在进行扫描填充时会使变量Label的值一直为真,从而出现该点右侧出现“拖尾”现象。如图1所示。
2.2 水平边问题
当水平直线的像素点个数为偶数时,不会影响填充效果;当像素点个数为奇数时,就会出现填充错误,如图2所示。
2.3 多边形边界线扫描转换时的问题
边标志算法实现的第一步是对多边形的边界线做上标记,但是这种情况在遇到边界线斜率的绝对值小于1时,直线与同一扫描线之间的交点个数就有可能出现奇数,因此这种情况仍然会出现类似水平边问题的填充异常现象。
2.4 狭长条问题
当两条相交直线的斜率非常接近时,其交点在数字显示器上的交点便会出现多个像素点,这时顶点附近的若干个像素点同样也会重合,与水平扫描线之间的连续交点个数也有可能出现奇数。因此,在进行填充时同样会出现类似于水平边问题的填充异常现象,如图3所示。
3 算法的改进
对上述问题深入分析,可以发现之所以会出现填充异常现象,是因为传统的边标志算法没有将普通的边界点与上述问题中的像素点区别开来。本文提出的新的改进方法的主要思想为:在对多边形的每一条边进行光栅化时,使用label(初始值为0)标记是否为多边形的边界,首先存储单元中取出当前像素点的label值,然后对当前需要标记的像素点的label值进行加1,然后在存放到当前像素点的label值的位置。依次对对每一条边进行光栅化。在对多边形内部区域进行填充时,起先读出当前像素点的label值,当前像素点的label值若是1,则读取当前像素点的水平方向的左侧和右侧像素点的label值,如果他们的值都为1,则布尔变量inner的值不变,否则取反。填充颜色时若当前像素点的label值大于0或者inner为真时,则填充为填充色,不然填充为背景色。如对于图1中的A点和B点,在对两点所在边界光栅化之后他们的label值等于2是大于1的,所以在填充颜色时将A和B点填充为填充色。又因为其前后两个像素点的label值不都为1,所以inner的值仍为假,从而该点右边的像素点不填充。
4 验证
通过多次实验的验证可以发现,改进之后的算法避免了在扫描填充时反复调用边表结构的问题,仅仅使用对边界像素点的标记值加1的操作即可实现上述问题中多边形的正常填充。无论从硬件实现还是从软件实现,改进后的边标志算法比原来算法在运行效率上都有相当的提高。
参考文献
[1]D.F.罗杰斯(梁友栋,石教英,彭群生译).计算机图形学的算法基础[M].北京:科学出版社,1987.
[2]张志龙,李吉成,沈振康.一种新的快速复杂连通区域扫描线填充算法[J].计算机工程与应用,2004,40(31):6-8.
[3]吳章文,杨代伦,勾成俊,等.区域填充极点判别算法[J].计算机辅助设计与图形学学报,2003,15(08):979-983.
作者简介
王利祥(1987-),男,河南省濮阳市人。硕士学位。主要研究方向为电子与通信工程、嵌入式计算。
作者单位
河南护理职业学院网络管理中心 河南省安阳市 455000

