城区物流配送中心选址优化系统设计与实现
郭 鹏,周 洋,周 峰,胡理嫚,马宸昊
(1.西南交通大学机械工程学院,四川成都 610031;2.西南交通大学经济管理学院,四川成都 610031)
,
min f2= τf1+ θ ,
,
f=f′+f3=f1+f2+f3。
城区物流配送中心选址优化系统设计与实现
郭 鹏1,周 洋1,周 峰1,胡理嫚1,马宸昊2
(1.西南交通大学机械工程学院,四川成都 610031;2.西南交通大学经济管理学院,四川成都 610031)
为了提高城区物流配送中心选址效率,克服传统方法须依靠人工计算的弊端,提出利用在线地图获取路径距离信息的方法。基于配送中心的实际建设和运营情况,确定配送中心选址问题的成本影响因素,设计选址优化系统框架,构建以总成本最小化的数学模型,采用基于整数编码的遗传算法对其进行求解。利用C#语言实现系统架构,并进行计算测试。测试发现:所构建系统能够自动获取城区各节点距离信息,较之传统手段减少了规划人员的工作量,围绕2类算例实施优化选址,均在较短时间内获得了切实可行的选址方案。结果表明,所提出的系统架构具有有效性和适用性,能够有效帮助规划人员实施物流节点选择。
物流系统管理;物流配送中心;选址优化;遗传算法;在线地图
随着国内外企业竞争日趋激烈,资源成本和人力成本越来越接近,物流作为企业经营成本中的重要组成部分已经越来越受到重视。在提高物流服务水平和降低物流成本方面,物流配送中心地址的选取,尤其是城区物流配送中心位置的选取非常重要。据统计,中国2014年物流运输费用占社会物流总费用的52.9%,保管费用占社会物流总费用的34.9%,两项之和高达87.8%[1]。如何对物流配送中心进行有效规划以降低物流保管和配送费用,成为政府管理机构面临的难题,同时城区物流需求急剧增长,现代物流对网点布局的要求越来越高。
物流配送中心选址问题作为供应链网络设计的主要内容广受关注[2-3]。问题可简化为设施选址问题,旨在从一系列备选点中选择一部分作为仓库的位置,在满足空间及容量约束的情况下,最小化投资的费用。由于该问题属于NP-hard,目前大量的研究均采用元启发式算法对其求解,诸如模拟退火算法、禁忌搜索算法、遗传算法、蚁群算法及萤火虫算法等群集智能优化技术[4-8]。此外,分支定界及分支定价一类的精确求解算法也得到改进,试图去求解更大规模的问题[9-12]。物流服务能力也被纳入优化指标中加以考虑,以更好地适应易腐食品的处理和应急服务[13-14]。遗传算法在求解物流配送中心选址问题上,性能表现优异,被广泛采用[15-17]。现有物流配送中心选址研究大多先确定备选点,而后手工计算备选点之间的距离,以此作为选址的距离矩阵。备选点及距离矩阵的确定需要耗费大量的时间去调研,使得决策人员难以在短期内做出合理的选址算例,将地理信息系统应用到选址中是缩短调研时间的良方[18],但仍然需要手动确定路网结构。
针对获取现有研究路径距离信息困难这一问题,本研究提出利用在线地图API获取路径距离信息的方法,以求提高选址效率和求解的准确性。在地图上确立备选点后,自动获取各点之间的距离信息。通过利用遗传算法求解问题的数学规划模型来获得最优选址算例。借助C#语言开发系统软件,仿真计算结果表明提出的选址优化系统的有效性和适用性。
1 城区物流配送中心选址优化系统

图1 物流配送中心网络框架
Fig.1 Frame of logistics distribution center network
城区物流配送中心是指以城市区域作为配送范围,能承担多品种、少批量、多用户配送的配送中心,其服务的对象大多是生产企业、经销商、零售商、连锁店[19]。在本研究设计的系统中,假设在某一区域内有n个需求点,拟建立m个物流配送中心来满足顾客的需求,在城区周边已有q个物流基地,其网络结构如图1所示。物流配送中心选址需要从大量的备选点中找出其最佳的建设位置,以满足顾客的需求。在选址过程中需要地价、运输费用和配送中心运营费用等成本因素,以总成本最低为目标,来确定最优的配送中心备选点选取算例。
在所提出的选址优化系统中,通过手动添加或者读取数据文件获得物流基地和顾客点的关联参数,如最大物流存储量、需求量、运费等。在百度地图上点选位置来获得配送中心备选点,并对各点附加相应的参数(运费、地价等),系统自动读取百度地图中提供的各点之间的路径信息。一旦完成参数的输入,系统则调用遗传算法实现对选址优化模型的求解。当满足遗传算法的终止条件时,则输出选址算例,并在地图窗口加以显示。
从上述系统工作的过程中,可以看出各个备选点间的距离信息是影响运费的关键因素。在问题的求解过程中,距离信息的读取由于要调用网络数据而需要消耗一定的时间。遗传算法作为优化求解的工具,可视为系统的核心组成部分,其迭代求解需要一定时间方能给出较好的选址算例。
2 地区物流配送中心选址优化模型
物流配送中心处在配送网络的中间环节,需同时考虑物流基地(供应点)和需求点的影响。在本研究考虑的城区物流配送中心选址问题中,配送中心备选点所处区域的地价、建设成本和单位运营成本均可通过调研或查询政府统计数据获得。每个需求点只能由某个配送中心完成所有货品的配送。通常配送中心物流量越大,其单位面积库存量越高,不同货品种类对于运输造成的影响不予以考虑。在引入模型之前,先介绍3个决策变量:zi若为1,表示对应的备选配送中心将投资建设,否则不予以投资;xij若为1,表明需求点j由配送中心i配送,否则由其他配送中心服务;yki为从物流基地k到配送中心i的运量。
对于管理部门而言,最重要的指标就是综合成本。城区物流配送中心的成本可分成3类,即建设成本、运营成本和运输成本。配送中心的建设成本包括土地购置费和物理设施建设费。根据配送中心的年物流量、单位面积库存量和周转率可以计算得到配送中心所需的面积。在已知配送中心单位面积建设成本和不同位置的单位面积地价时,可以得到建设成本的目标函数f1,总建设成本最小。

(1)

配送中心的运营费用包括人工费用、仓储费用和折旧费用等。如果考虑所有因素,模型将变得十分复杂。由于运营费用与配送中心的规模呈正相关关系,将其简化为与建设成本呈线性相关的函数,便于计算。目标函数f2,总运营费用最小。
minf2=τf1+θ,
(2)
式中:τ=0.035,为相关系数;θ=300,为货物的修正值。
根据物流基地、配送中心及需求点的经纬度利用百度地图API可得到相互之间的实际距离。结合物流基地与配送中心、配送中心与需求点之间的单位运输成本可得到运输费用函数f3(目标函数),总的运输费用最小。

(3)

目标函数f2取决于目标函数f1,因此可将其合并为一个目标函数f′=f1+f2;目标函数f3独立于函数f′,且2个目标一致,各自权重均设为1,于是总目标函数f为
f=f′+f3=f1+f2+f3。
(4)
以下约束在建模时也须考虑:
1) 从物流基地供应给配送中心的各类货品总数不能超过其最大供应量;
2) 待建配送中心的货品总量进出相等;
3) 每个需求点有且只能由某个配送中心进行服务;
基于上面的描述,其数学模型为
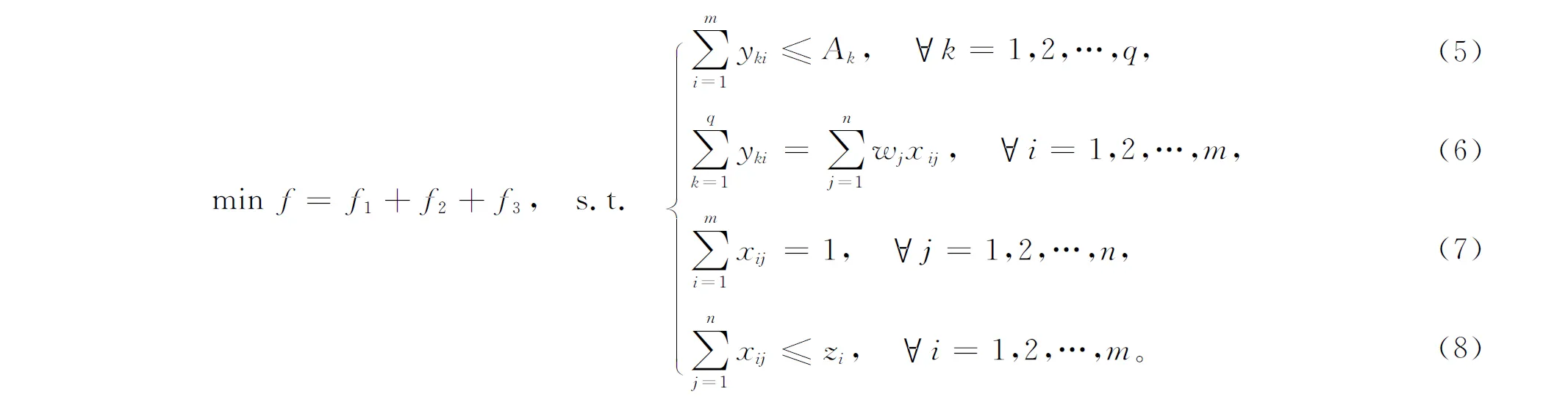
约束(5)表示从物流基地运输到配送中心的各类货品总数不超过其最大供应量Ak;约束(6)表示待建配送中心的货品总量进出相等;约束(7)表示每个需求点有且只能由一个配送中心进行服务;约束(8)表示需求点只能由其所属的配送中心配送。
3 配送中心选址优化设计
由于选址问题是NP-hard的,采用分支定界等精确算法求解难度较大。为此本研究提出利用遗传算法来进行优化,以求在合适的计算时间内获得高质量的解。
3.1 遗传算法
遗传算法对问题种类有很好的鲁棒性,该算法在函数优化、组合优化、自动控制、机器学习、图像处理、人工生命、遗传编码与机器学习等方面都得到了广泛的应用[20]。遗传算法的求解步骤如下。
1)编码 遗传算法在迭代之前,需要先将解空间的数据表示成遗传空间的基因型个体,个体结构的不同组成即为不同的点。通过采用整数编码表示方式,让每一个基因对应一个需求点,其数值表示该需求点由相应的配送中心服务。如个体V=(1, 1, 3, 3, 1)表示需求点1,2,5由配送中心1服务,需求点3,4由配送中心3服务。
2)种群初始化 初始种群作为遗传算法迭代的起始,其能够通过随机方式或结合问题的特性产生,在此以随机方式产生。
3)选择操作 系统采用随机选择方法,从种群中选择3个个体,然后将适应度最佳的个体复制到新一代种群中,并在选择过程中保留最佳个体,以此保证当前种群适应度最佳的个体总能在迭代中生存。适应性函数直接采用目标函数,也就是说目标函数值越小的个体,其适应度越佳。

图2 交叉操作
Fig.2 Crossover operation
4)交叉操作 交叉操作作为遗传算法产生新种群的重要步骤,常见的手段有单点交叉、两点交叉和多点交叉等[21]。基于本问题的编码特性,在此选用两点交叉。随机产生2个断点位置,交换父代个体断点之间的基因即得到新的子代个体,如图2所示。
5)变异操作 变异操作能增加种群多样性,避免算法过早收敛。随机选择一个个体,对该个体以一定的变异概率随机改变其基因位上的值,来实现新个体的产生。
6)个体重置操作 通过比较子代个体与上一代个体的适应度值,如果连续给定次数没有改善个体质量,则随机产生新的个体对其进行替换。通过迭代操作,达到种群的寻优目的。如果迭代次数超过指定的次数则停止操作,并将当前种群最优个体作为最终的解输出到系统中;否则,继续循环上述的选址、交叉和变异操作。
通过初步计算实验,遗传算法选用以下参数能够获得较好的性能:种群大小为100,交叉概率为0.8,变异概率为0.2,最大迭代次数为500,连续未改善次数为50。
3.2 系统开发设计
通过利用C#语言对选址优化系统进行实现,使用WindowsForms开发窗口应用。程序窗体分成地图显示和信息输入2个部分。地图部分使用百度地图API显示城区信息,可根据所显示的情况在地图上自由点选位置点作为物流基地、配送中心备选点及需求点。信息的输入与显示部分则在点选完成后输入具体的参数信息。由于窗口显示空间有限,将物流基地、配送中心备选点和需求点的信息分为3栏显示和输入。考虑程序的适用程度,各点的参数都由使用人员自行输入与修改。在完成所有信息的输入后,利用ASP.NET向百度服务器发出请求,获取各点之间的距离,建立距离矩阵。而后将所有数据导入遗传算法进行寻优。在达到迭代终止条件后输出计算结果。
该选址系统与一般选址方法相比,增加了人机交互界面,将网络访问和选址优化等进程进行了封装,只需在程序窗体进行操作,降低了管理人员的使用难度;结合百度地图更方便快捷的选点方式,使选点过程的速度加快,选点的可靠性提高;还可显示各备选点的经纬度。
4 算例及分析
选取成都市某地区为计算区域,在此区域上选取若干备选配送中心,配送中心备选点规模分别为5,10,标记为算例1,2,其中算例1和算例2物流基地的供应量等于所有需求点需求量之和,对于配送中心不限制其供应规模。参数αi由式(9)求得:
(9)
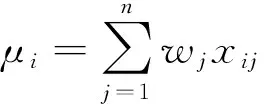
表1为算例1与算例2的需求点对应的需求量。表2给出了备选配送中心的关联参数,如调整系数、占地面积参数、运费等。表3列出了选点后每个位置点的经纬度坐标,便于调用百度地图获取路径距离。各类设施具体位置在地图上的标注如图3所示,其中圆点表示物流基地,菱形表示配送中心备选点,三角形表示需求点。算例2只在表1中列出了各个需求点的需求量,与算例1不同之处仅仅是其物流基地数目比算例1多1处。算例2各个备选配送中心的地价取值如表4所示。图4给出了算例2各类设施在地图上的具体位置。

表1 需求点的需求量

表2 备选配送中心关联参数

表3 各类设施对应的地理位置坐标
将上述参数输入选址优化系统进行求解,获得了算例 1及算例2的结果。在算例1中,备选配送中心1,3,5不 被采纳。配送中心2负责1,4,5的物流配送任务,配送中 心4则负责完成剩下所有需求点的物流配送任务。在此 情况下,总成本最低,为2 943 121.77元。在算例2中,所 有需求点的货物都由5号配送中心提供,总成本为 106 724 751 978.02元。
2个算例结果的区别源于计算规模较小、随机选点和 未规定配送中心的最大规模。在实际情况下,物流配送中 心由于各种因素会限制其最大规模,而在简化模型中只考虑其物流量与满足该物流量所需的建设成本,使得出现了单个配送中心满足所有需求点的情况。当算例的 规模较小,且只有一个物流基地时,若配送中心到需求点和物流基地到配送中心之间的运费差距不大,备选 点之间竞争不明显。为了总成本最小,只选择一个备选配送中心显然优于选择两个备选配送中心的,即算例 2中所出现的结果。若案例规模较大,且不止一个物流基地时,备选点的选择由于运费差异较大就导致了选 择的多样化。

图3 算例1各设施地理分布
Fig.3 Geographic distribution of the facilities for instance 1
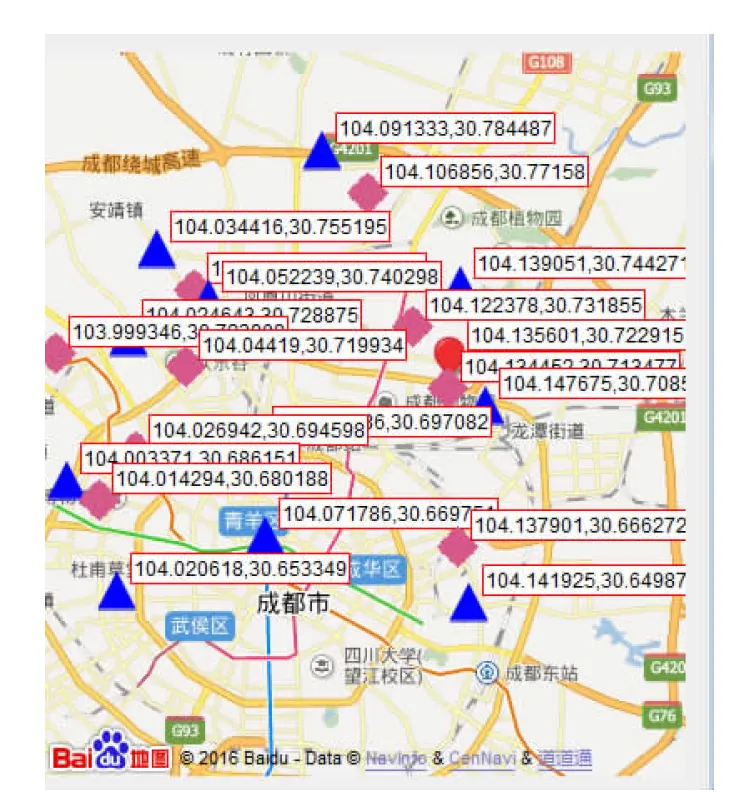
图4 算例2各设施地理分布
Fig.4 Geographic distribution of the facilities for instance 2
虑其物流量与满足该物流量所需的建设成本,使得出现了单个配送中心满足所有需求点的情况。当算例的规模较小,且只有一个物流基地时,若配送中心到需求点和物流基地到配送中心之间的运费差距不大,备选点之间竞争不明显。为了总成本最小,只选择一个备选配送中心显然优于选择两个备选配送中心的,即算例2中所出现的结果。若案例规模较大,且不止一个物流基地时,备选点的选择由于运费差异较大就导致了选择的多样化。

表4 算例2备选配送中心地价
由于系统需要调用百度地图API获取实际道路进行求解,因此求解时间上较直接采用直线距离求解耗时多。但该系统将优化计算与实际车辆路径信息结合,改进了现在大多数文献研究中的距离假设。因此在选址规划时能够大大降低调研数据的工作量,在实际中更加简易、适用。
5 结 语
本文基于实际情况,提出了城区物流配送中心选址模型,针对传统研究中需提前确定备选点和需求点以及物流基地和备选点之间的距离矩阵的弊端,提出利用百度地图获取车辆路径距离信息的方法。在融合遗传算法的基础上,利用C#开发了选址优化系统。计算测试表明,采用在线地图的API获取距离矩阵能够极大降低管理人员的工作量,并有效提高规划精度。后期研究将考虑采用混合算法进一步改善优化过程,以求获得更好的优化效果。此外,将更多的影响因素融入到系统中也是可以进一步探讨的内容。
/References:
[1] 何黎明. 中国物流年鉴:2014年中国物流运行情况分析[M]. 北京: 中国财务出版社, 2015.
[2] SAHIN G, SURAL H. A review of hierarchical facility location models[J]. Computers & Operations Research,2007, 34(8): 2310-2331.
[3] MELO M T, NICKEL S, SALDANHA D G F. Facility location and supply chain management:A review[J]. European Journal of Operational Research,2009, 196(2): 401-412.
[4] MAA J R, KADIPASAOGLU S N, KHUMAWALA B M. An empirical comparison of Tabu search, Simulated Annealing, and Genetic Algorithms for facilities location problems[J]. International Journal of Production Economics,2006, 103(2): 742-754.
[5] GRIFFIS S E, BELL J E, CLOSS D J. Metaheuristics in logistics and supply chain management[J]. Journal of Business Logistics, 2012, 33(2): 90-106.
[6] 李昌兵,杜茂康,曹慧英. 基于层次遗传算法的物流配送中心选址策略[J]. 计算机应用研究,2012, 29(1): 57-59. LI Changbing, DU Maokang, CAO Huiying. Location strategy of logistics distribution centers based on hierarchical genetic algorithm[J]. Application Research of Computers, 2012, 29(1):57-59.
[7] 王坤. 蚁群算法物流配送中心选址优化仿真研究[J]. 计算机仿真,2012, 29(4): 251-254. WANG Kun. Location technology research of logistics distribution based on ant colony optimization algorithm[J]. Computer Simulation, 2012, 29(4):251-254.
[8] FERNANDES D R M, ROCHA C, ALOISE D, et al. A simple and effective genetic algorithm for the two-stage capacitated facility location problem[J]. Computers & Industrial Engineering,2014,75(1): 200-208.
[9] KLOSE A, GORTZ S. A branch-and-price algorithm for the capacitated facility location problem[J]. European Journal of Operational Research,2007, 179(3): 1109-1125.
[10]DUPONT L.Branch and bound algorithm for a facility location problem with concave site dependent costs[J]. International Journal of Production Economics,2008, 112(1): 245-254.
[11]YANG Z, CHU F, CHEN H. A cut-and-solve based algorithm for the single-source capacitated facility location problem[J]. European Journal of Operational Research, 2012, 221(3): 521-532.
[12]BERESNEV V. Branch-and-bound algorithm for a competitive facility location problem[J]. Computers & Operations Research,2013, 40(40): 2062-2070.
[13]李艳,谢能刚,王付宇,等. 物流配送中心多目标优化选址的仿真设计[J]. 计算机仿真,2012, 29(7): 234-237. LI Yan, XIE Nenggang, WANG Fuyu,et al. Simulation design of logistics distribution center multi-objective optimization location[J]. Computer Simulation,2012, 29(7): 234-237.
[14]肖俊华,侯云先. 带容量限制约束的应急设施双目标多级覆盖选址模型及算法[J]. 计算机应用研究,2015, 32(12): 3618-3621. XIAO Junhua, HOU Yunxian. Capacitated bi-objective emergency facility location model and algorithm considering multi-level gradual coverage[J]. Application Research of Computers, 2015, 32(12): 3618-3621.
[15]吴兵,罗荣桂,彭伟华. 基于遗传算法的物流配送中心选址研究[J]. 武汉理工大学学报(信息与管理工程版),2006, 28(2): 89-91. WU Bing, LUO Ronggui, PENG Weihua. Choice of logistics distribution center based on genetic algorithm[J]. Journal of Wuhan University of Technology(Information & Management Engineering), 2006, 28(2): 89-91.
[16]赵冬玲,孔志周,官东. 基于改进遗传算法的物流配送中心选址研究[J]. 统计与决策,2008(11): 153-155.
[17]李绍斌,杨西龙,李耀庭,等. 基于遗传算法的多军事物流配送中心选址决策[J]. 物流技术,2015, 34(21): 213-215. LI Shaobin, YANG Xilong, LI Yaoting et al. Study on decision-making concerning location allocation of multiple military logistics distribution centers based on genetic algorithm[J]. Logistics Technology, 2015, 34(21): 213-215.
[18]林娜,李志. 基于GIS和遗传算法的物流配送中心选址研究[J]. 遥感信息,2010(5): 110-114. LIN Na, LI Zhi. Study on location selection of logistics distribution center based on GIS and genetic algorithm[J]. Remote Sensing Information, 2010(5): 110-114.
[19]冯耕中,李毅学,华国伟. 物流配送中心规划与设计[M]. 西安: 西安交通大学出版社, 2011.
[20]席裕庚,柴天佑,恽为民. 遗传算法综述[J]. 控制理论与应用,1996, 13(6): 697-708. XI Yugeng, CHAI Tianyou, YUN Weimin. Survey on genetic algorithm[J]. Control Theory and Applications, 1996, 13(6): 697-708.
[21]CAUTY R. Genetic algorithms and engineering optimization[J]. Wiley,1997,43(4):379-381.
Design and implementation of urban logistics distributioncenter location optimization system
GUOPeng1,ZHOUYang1,ZHOUFeng1,HULiman1,MAChenhao2
(1.SchoolofMechanicalEngineering,SouthwestJiaotongUniversity,Chengdu,Sichuan610031,China; 2.SchoolofEconomicsandManagement,SouthwestJiaotongUniversity,Chengdu,Sichuan610031,China)
Inordertoimprovetheefficiencyofurbanlogisticsdistributioncenterlocationselection,andtoovercometheshortcomingsofthetraditionalmethodbasedonhumanaidedcalculation,theonlinemapisusedtoobtainthepathdistanceinformation.Consideringthepracticalconstructionandoperationsituationofthelogisticsdistributioncenter,thecostrelatedimpactfactorsaredeterminedandthelocationoptimizationframeisdescribed.Thenthemathematicalformulationisproposedforminimizingthetotalcost,andthegeneticalgorithmbasedonintegercodeisdesignedtosolvetheproblemunderconsideration.ThecorrespondingsystemisimplementedbyC#language.Thesystemistestedbasedonthepracticaldata,andthecomputationalresultsdemonstratethattheproposedsystemcanautomaticallyobtainthedistanceinformationbetweenvariousnodesandperformthelocationoptimization.Finallytheoptimalfeasiblelocationschemeisdeliveredbytheproposedsystem.
logisticssystemsmanagement;logisticsdistributioncenter;locationoptimization;geneticalgorithm;onlinemap
1008-1542(2017)01-0019-07
10.7535/hbkd.2016yx06006
2016-04-17;
2016-06-28;责任编辑:张 军
国家自然科学基金(51405403);西南交通大学大学生科研训练计划项目(150208)
郭 鹏(1988—),男,四川南充人,讲师,博士,主要从事物流运作管理、设施选址优化方面的研究。
E-mail:pengguo318@gmail.com
TP
A
郭 鹏,周 洋,周 峰,等.城区物流配送中心选址优化系统设计与实现[J].河北科技大学学报,2017,38(1):19-25.GUOPeng,ZHOUYang,ZHOUFeng,etal.Designandimplementationofurbanlogisticsdistributioncenterlocationoptimizationsystem[J].JournalofHebeiUniversityofScienceandTechnology,2017,38(1):19-25.

