三浮陀螺伺服测试误差系数估计方法
王永彤,朱志刚,郭宗本,徐 超
(北京航天控制仪器研究所,北京100039)
三浮陀螺伺服测试误差系数估计方法
王永彤,朱志刚,郭宗本,徐 超
(北京航天控制仪器研究所,北京100039)
为了更好地解决工程实际中三浮陀螺极轴伺服测试时误差系数估计问题,采用了Kalman滤波和递推最小二乘的方法。试验结果证明,Kalman滤波方法能够有效地估计出极轴伺服测试时的陀螺误差系数。用统计检验的方法分析了该模型以及各系数的显著性,结果显示对Dvz和Dzz的估计是显著的。
三浮陀螺;伺服测试;Kalman滤波;误差系数估计;显著性分析
0 引言
伺服转台测试是高精度单自由度机电陀螺测试方法之一,该方法的优点是:1)测试精度不受陀螺力矩器精度的限制;2)精度潜力大,由于不直接测量漂移角速度,而是测量漂移角速度随时间的积分,在一定程度上可以用时间换精度;3)测量过程更接近陀螺在平台系统中的工作状态,对实际应用有更好的指导意义。为提高测试精度、丰富陀螺精度鉴定手段,以及给更高精度机电陀螺奠定测试技术基础,提高工程化应用,亟待开展陀螺的伺服转台测试方法、数据处理及误差系数标定的研究。
当陀螺输入轴平行地理极轴做伺服测试时,陀螺误差系数的辨识可以采用谐波系数法、最小二乘估计法和Kalman滤波估计方法[1]。用谐波系数法时,需要陀螺沿输入轴相对地理系旋转至少一周才能解出误差系数,由于耗时长、实时性差,难以满足工程应用。最小二乘估计法使量测估计的精度达到最佳,不使用与估计量有关的动态信息和统计信息,优点是算法简单,在对被估计量和量测误差缺乏了解的情况下仍能适用[3]。Kalman滤波是线性最小方差估计,使用时需要知道被估计量驱动噪声的统计特性、系统状态方程,以及量测噪声的统计特性[3]。最小二乘和Kalman滤波各有优缺点,为提高陀螺误差系数的估计精度,提升陀螺伺服试验效率,同时解决估计方法在实际测试中的实用性,还需进行对比研究。本文根据陀螺漂移的实际特性并结合极轴伺服测试时的特点采用了与主轴角度相关的陀螺误差模型,并在此基础上采用Kalman滤波器与最小二乘法对模型参数进行辨识。随后,对模型的回归方程及各系数进行了显著性分析。
1 陀螺极轴伺服试验
三浮陀螺在1g重力场下误差模型如式(1)所示[1]:

式中,ωd为陀螺的综合漂移,(°)/h;Df为不敏感比力的漂移角速度,(°)/h;Dx、Dy、Dz为与重力加速度成比例的误差系数,(°)/h/g;Dxx、Dzz为与重力加速度平方成比例的误差系数,(°)/h/g2;Dxy、Dxz、Dyz为与重力加速度乘积成比例的误差系数,(°)/h/g2;gx、gy、gz分别为沿x轴、y轴、z轴的重力加速度分量,g;ωm为陀螺的动态相关噪声,(°)/h;ωε为陀螺误差模型残差,(°)/h。
x、y、z分别对应陀螺仪的输入轴IA,输出轴OA,自转轴SA。
陀螺伺服测试时常采用极轴伺服试验考察陀螺的精度[1]。陀螺极轴伺服试验有两种安装方位:陀螺仪输入轴平行极轴指北和指南。陀螺仪坐标系在地球坐标系(O′XYZ)和地理坐标系(OXeYeZe)中的方位如图1所示。在这种安装方式下,陀螺始终敏感地速。重力在陀螺输入轴上投影为常值,在陀螺自转轴和输出轴上投影根据转台主轴转动的角位置呈现周期性变化。
在图1中,φ为当地纬度;ωe为地球转速;O′XYZ为地球坐标系;OXeYeZe(OUNW)为地理坐标系,OXe指天,OYe在当地水平面内指北;oxyz为陀螺仪坐标系,ox、oy、oz分别为陀螺仪的输入轴IA、输出轴OA、自转轴SA;OX2Y2Z2为伺服转台主轴坐标系,OX2、OZ2分别为转台主轴、耳轴,转台零位时OX2与OXe重合,OY2指向OZe反向,OZ2与OYe重合。

图1 极轴伺服试验陀螺仪坐标系方位图Fig.1 Coordinates in servo test
陀螺极轴伺服试验时,有如下运动方程:

其中,˙θ为转台绕转台主轴的旋转角速度,可由角度差分得到,(°)/h;ωx为地速在陀螺输入轴上的投影,(°)/h。
陀螺仪输入轴平行极轴指北的零位方位定义为:陀螺输入轴IA平行极轴指北,马达轴SA指东。重力加速度g朝上为正,伺服转台沿主轴坐标系OX2轴逆时针转动为正,转角为θ,正东方向为角度起始零位。地速在陀螺输入轴上投影为ωe,重力加速度在陀螺各轴上的投影如下:
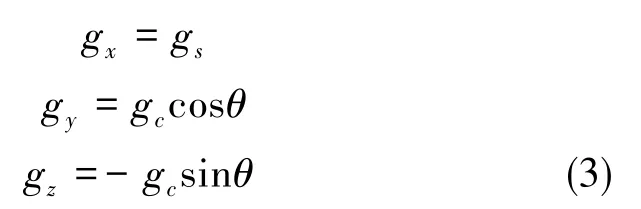
其中,gs=gsinφ,gc=gcosφ。
陀螺仪输入轴平行极轴指南的零位方位定义为:陀螺输入轴IA平行极轴指南,马达轴SA指东。地速在陀螺输入轴上投影为-ωe,重力加速度在陀螺各轴上的投影如下:
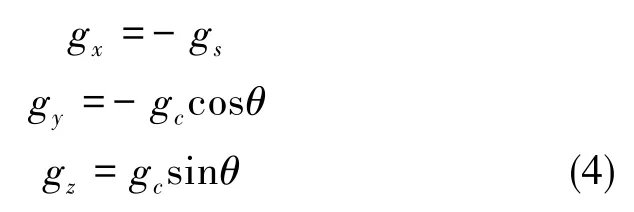
将式(3)带入式(1)后采用谐波分析的方法,得到陀螺漂移是一个关于转台转角θ的周期函数。陀螺漂移可以用式(5)表示,整理后得式(6),式中各系数分为与转台转角无关的项、与转台转角一次谐波有关的项、与转台转角二次谐波有关的项。
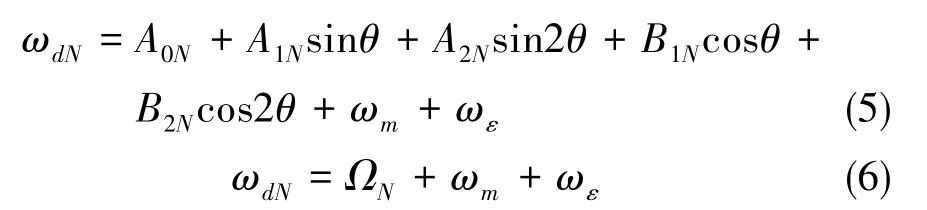
其中,
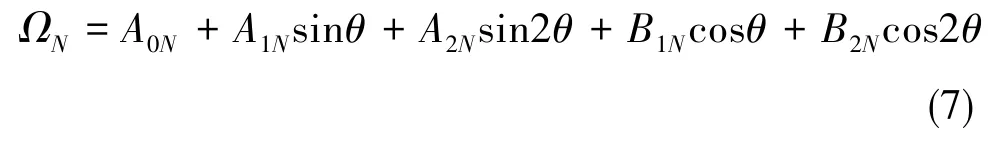
ωdN为陀螺输入轴指北时的综合漂移。
其中,A0N、A1N、A2N、B1N、B2N如式(8)所示。

同理可得到陀螺输入轴指南时的谐波系数方程,A0S、A1S、A2S、B1S、B2S如式(9)所示。陀螺误差系数可由谐波系数通过代数运算解出,因此辨识误差系数的关键是得到谐波系数。

2 伺服测试陀螺误差系数估计方法
2.1 Kalman滤波估计方法
三浮陀螺动态相关噪声ωm为1阶马氏过程,其相关函数为:
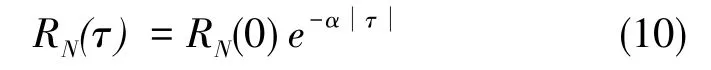
其中,RN(0)为均方值,α为反相关时间常数,τ为两点之间的时间间隔。RN(0)和α可以通过试验进行估算[2]。
将其白化离散后的表达式[3]为:

其中,T为离散时间;wk为白噪声序列。
陀螺伺服测试时,陀螺漂移的系统模型和量测模型方程[1,3]分别为:
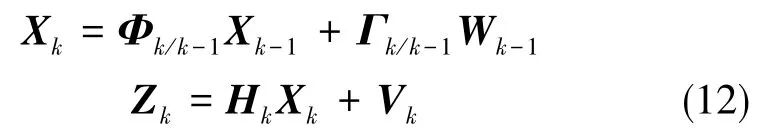
根据式(6)、式(7)和式(11)得到Kalman滤波方程中的各项如下:
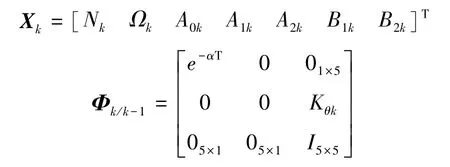
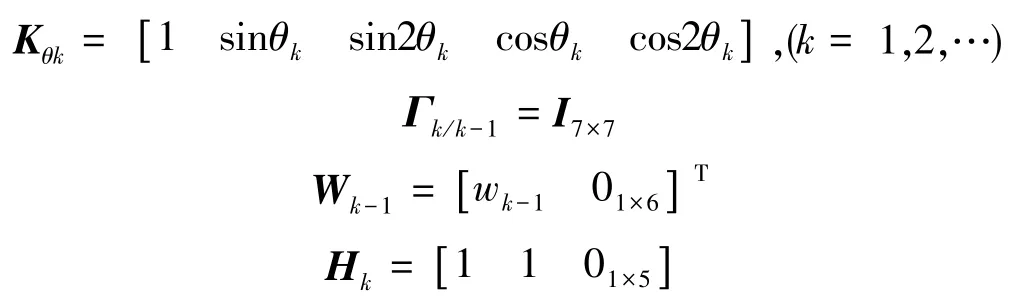
θk为k时刻伺服转台主轴角度。
观测量Zk为伺服转台角速率,由角度差分得出。Vk为伺服转台角速率的量测噪声,角速率的随机误差主要由测角误差造成,设测角误差的峰峰值为ε,ΔT为动平均时间[1],角速率读数误差最大值为ε/ΔT,此误差近似为正态分布,可视为白噪声。ΔT选取时需考虑角速率的平滑效果和陀螺动态误差的相关时间,这里为2000s。量测方差估计为:
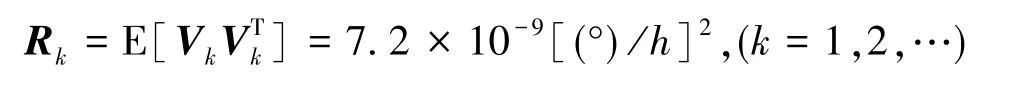
系统噪声方差为:
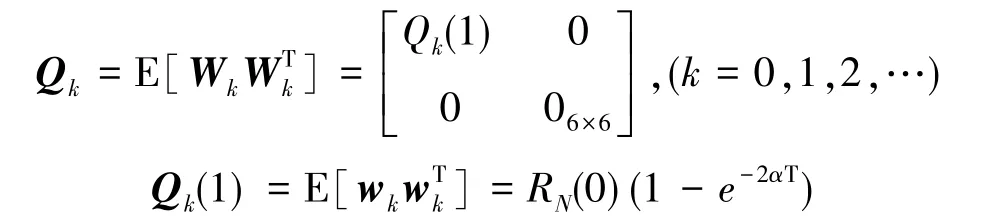
由试验数据计算可得,RN(0)=1.3×10-7[(°)/h]2,α=2000,T=1s。
Kalman滤波方程如下[1,3]:

X0和P0初始值均赋0。
2.2 最小二乘估计方法
为了对比Kalman滤波效果,对三浮陀螺误差系数用最小二乘方法进行估计,式(7)表达可以如式(14)所示,Zi为第i次转台角速度量测值,Vi为第i次随机量测噪声,Hi=[1 sinθisin2θicosθicos2θi],为提高数据处理效率,采用递推最小二乘方法[3]估计谐波系数。
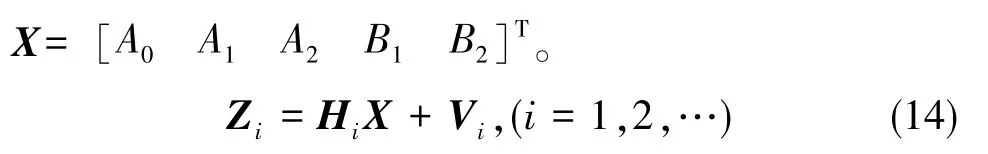
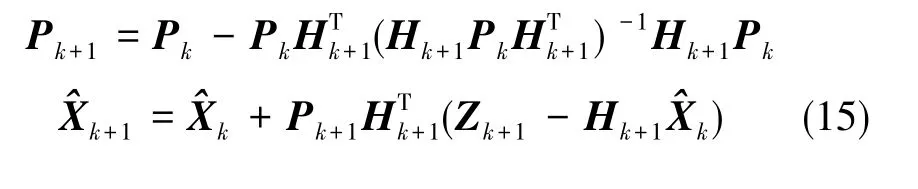
为避免估计误差跳跃剧烈,^X0和P0可由初始数据经最小二乘计算得到[3],如式(16)
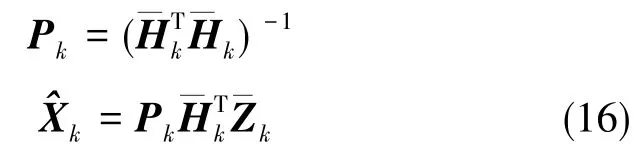
3 试验分析
3.1 试验数据分析
某陀螺极轴伺服试验的主轴角速度数据如图2和图3所示,采样时间为1s。为获取更多数据进行对比,测试时间较长。其中,输入轴指北、指南的数据样本长度分别为52.7h和39h,转台分别转过579.3°(1.61圈)和523°(1.45圈),转台绕主轴旋转一周分别为32.8h和26.9h。用Kalman滤波估计方法,陀螺相关噪声和谐波系数的收敛稳定时间均在6.5h左右,收敛时间占主轴旋转一周时间的21%和 26%。辨识结果如图4和图5所示。各谐波系数体现了所包含陀螺误差系数的综合精度,如式(8)、式(9)所示。用递推最小二乘估计方法辨识结果如图6和图7所示。为避免估计误差起伏剧烈,用前4000个数据做最小二乘估计,将其设为递推初值。各谐波系数收敛时间约为4.5h左右。将陀螺输入轴指北、南两次试验得到的谐波系数做代数运算后,可以得到陀螺各误差系数,结果如表1所示。

图2 陀螺输入轴指北时转台相对主轴角速度Fig.2 The angular velocity of the turntable which axis is parallel to the earth's north polar axis
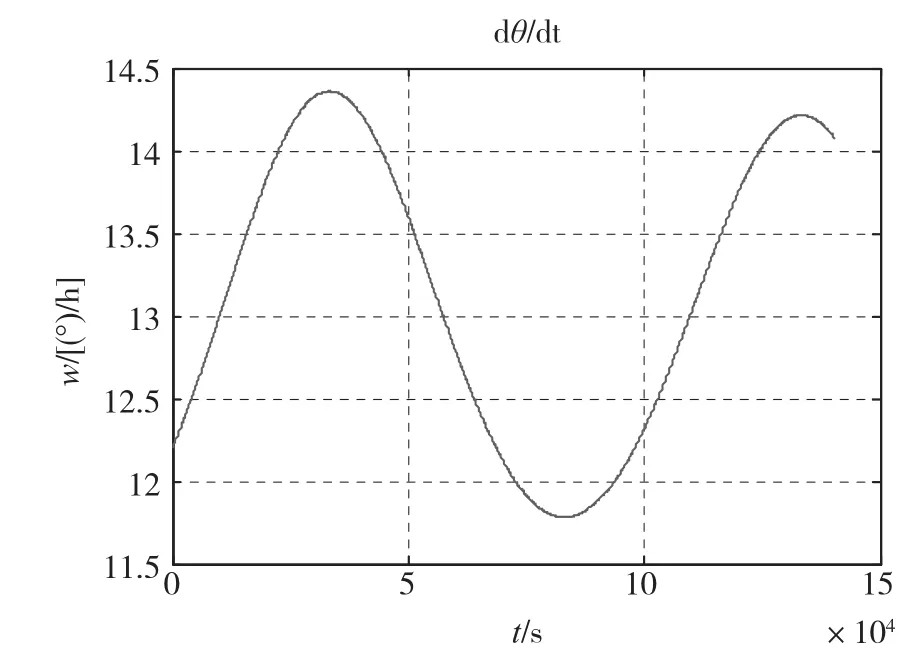
图3 陀螺输入轴指南时转台相对主轴角速度Fig.3 The angular velocity of the turntable which axis is parallel to the earth's south polar axis
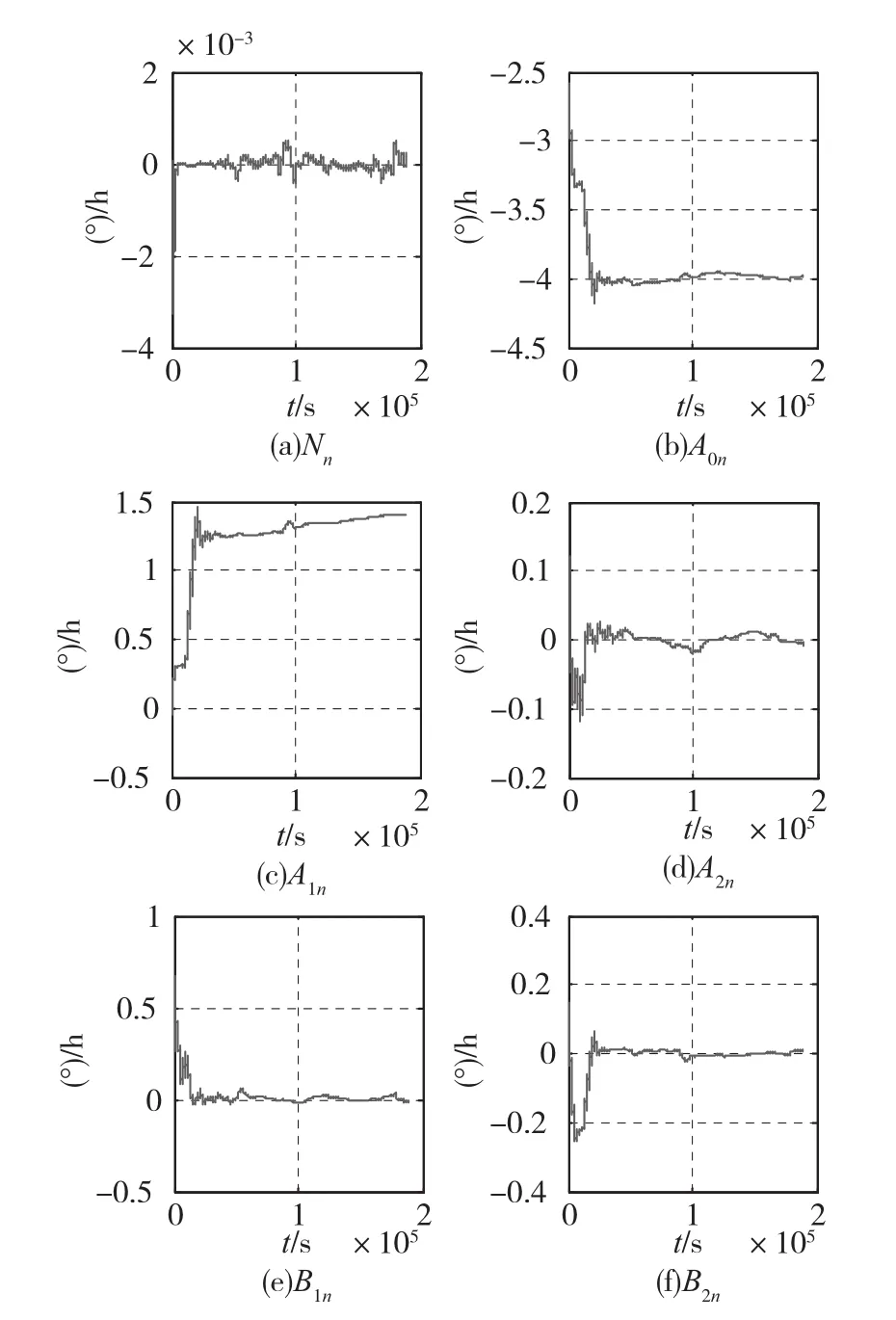
图4 陀螺相关噪声与谐波系数滤波收敛过程(陀螺输入轴指北)Fig.4 The identification results of the model(the turntable's axis is parallel to the earth's north polar axis)

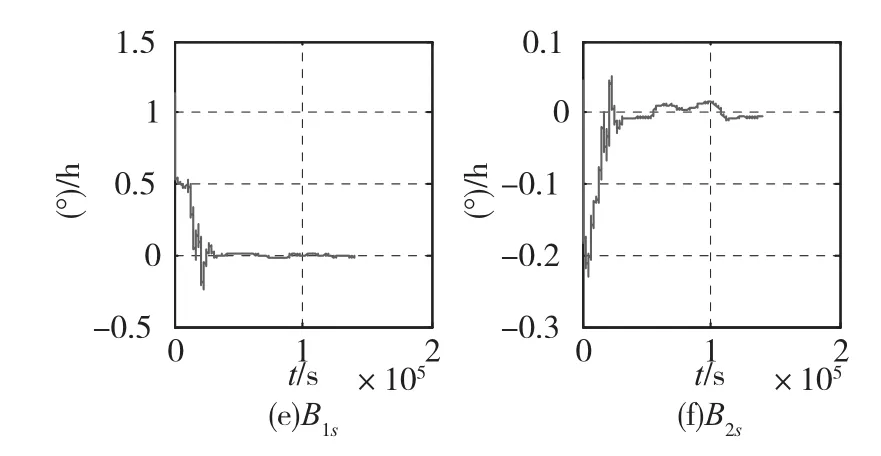
图5 陀螺相关噪声与谐波系数滤波收敛过程(陀螺输入轴指南)Fig.5 The identification results of the model(the turntable's axis is parallel to the earth's north polar axis)
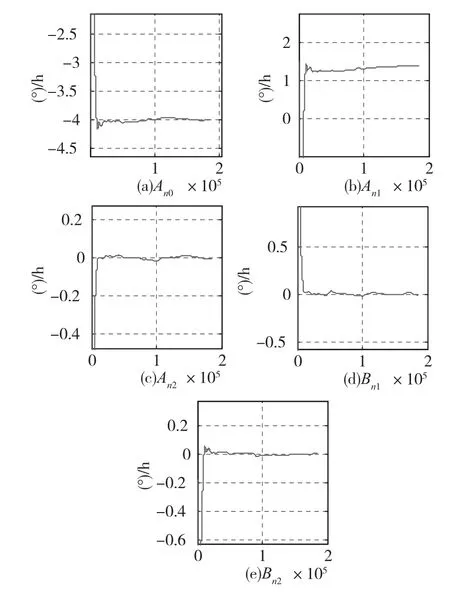
图6 用递推最小二乘法估计陀螺谐波系数收敛过程(陀螺输入轴指北)Fig.6 The identification results of the model by recursive least⁃squares(the turntable's axis is parallel to the earth's north polar axis)
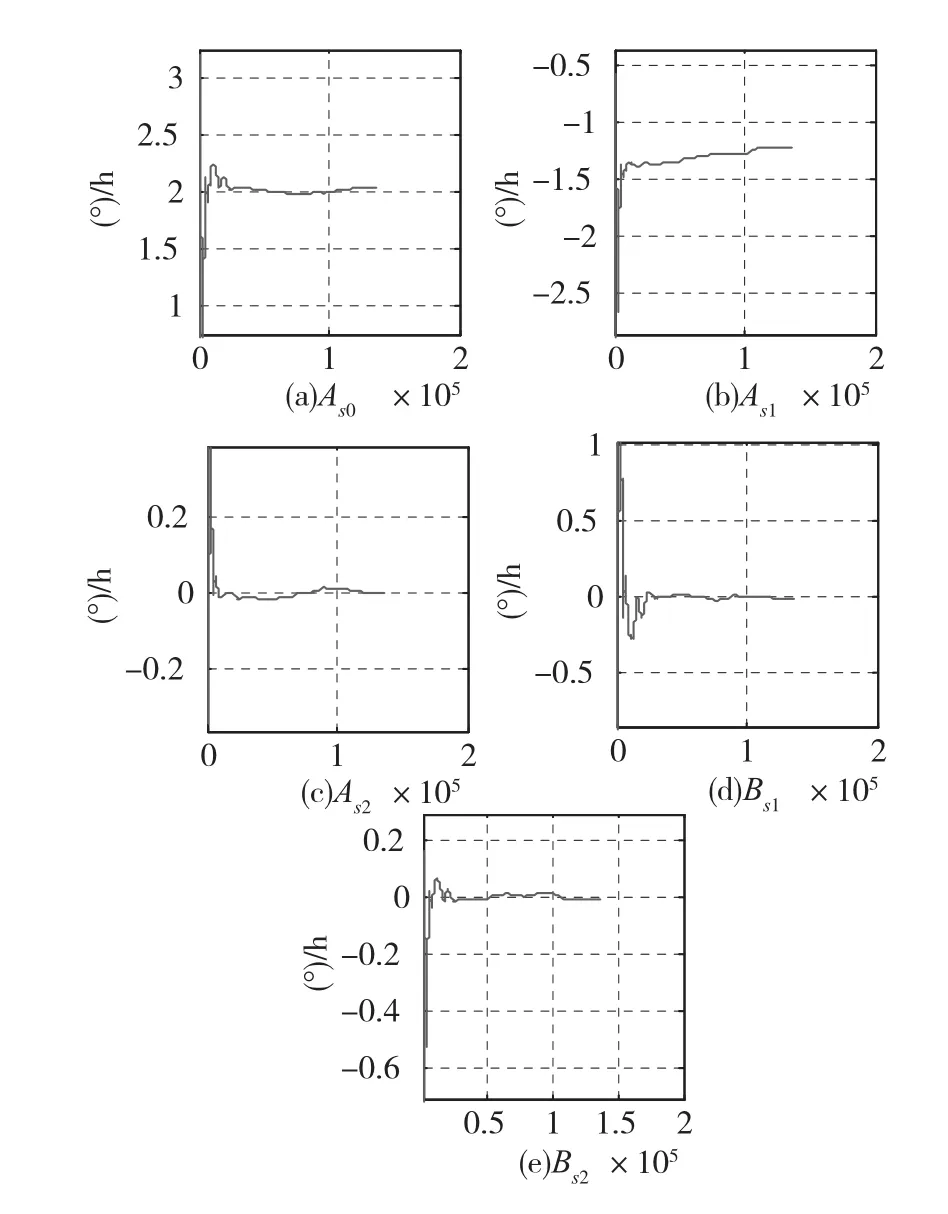
图7 用递推最小二乘法估计陀螺谐波系数收敛过程(陀螺输入轴指南)Fig.7 The identification results of the model recursive least⁃squares(the turntable's axis is parallel to the earth's south polar axis)

表1 陀螺误差系数估计结果(设Dxx=0)Table 1 The determined coefficients of Gyro(Dxx=0)
以陀螺输入轴平行极轴指北的数据为例,用Kalman滤波辨识的系数经拟合后与实测漂移相减的残差如图8所示,标准差如表2所示。与递推最小二乘的相比,Kalman滤波拟合后的残差标准差小,如图9所示。

图8 Kalman滤波拟合后的陀螺漂移残差Fig.8 The drift residuals with Kalman filter

表2 陀螺漂移角速度残差标准差(陀螺输入轴指北)[(°)/h]Table 2 The standard deviation of the gyro drift residuals(the turntable's axis is parallel to the earth's north polar axis)
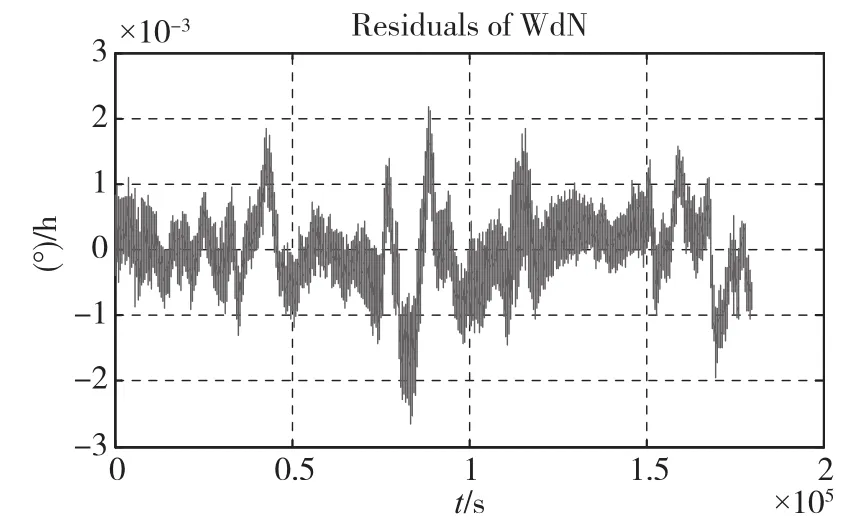
图9 最小二乘方法拟合后的陀螺漂移残差Fig.9 The drift residuals with LSM
3.2 显著性分析
估计出陀螺误差系数后,还需对误差方程及各系数进行统计检验。
假定第j次被测量yj和参数a0、a1、…、an之间呈线性关系n,j=1,2,…,N,N>n,xji为可测的已知变量,ai为n待估计的未知参数,ej是N个相互独立服从同一正态分布N(0,σ2)的随机变量。有观测方程Y=XA+ε。总偏差平方和为回归平方和为残差平方和为可证明ST=SR+SE。
如果变量y与xi之间没有线性关系,只需检验假设H0:a1=0,…,ai=0,这可以通过比较SR和SE来实现。可以证明X满秩和假设H0成立时,SR/σ2~χ2(n),SE/σ2~χ2(N-n-1),SR和SE相互独立,从而:

对给定的一组数据算得F>Fa,则在显著水平α下,认为回归方程是有显著意义的。反之,则认为该线性回归方程没有显著意义。
此外,还需对每个变量进行考察,如果某个变量对y作用不明显,在模型中它前面的系数ai可取值为0。检验因子xi是否显著可以等价于是服从正态分布的随机变量上的第i个对角元与SE相互独立,在假设H0∶ai= 0条件下,计算统计量:

如果F>Fa,则认为在显著水平α下回归系数显著,反之则认为不显著。
在估计陀螺误差系数时,根据陀螺极轴伺服试验的特点,XTX的最大值为5,因此将陀螺误差模型转化为式(14)。对该线性回归模型及各系数进行显著性检验。其中,y=ωd,a0、a1、…、an分别为A0、A1、A2、B1、B2,Vi近似为正态分布。
陀螺输入轴指北时,SEN=0.044,SRN=1.27× 105,N=129727,n=5,经计算得回归方程统计量FN=7.5×106,在显著水平α=0.01下,F0.01(5,129721)=3.02,因此认为回归方程是显著的。
再检验各误差系数。统计量F的下角标代表陀螺各系数,N指陀螺输入轴指北。对角元素pii计算为经计算得FA0N=5.8×1012,FA1N=3.4×1011,FA2N=2.8×104,FB1N=3.2×106,FB2N=9.5×104。在显著水平α=0.01下,F0.01(1,129721)=6.63。因此,各系数是显著的。当陀螺输入轴指南时,也能得出同样的结论。
4 结论
本文在三浮陀螺做极轴伺服测试时,用Kalman滤波器和递推最小二乘方法估计陀螺误差系数,并对最小二乘回归方程以及各谐波系数进行了显著性分析,试验结果表明:
1)所采用的Kalman滤波器是一致渐进收敛的,相对递推最小二乘方法,用Kalman滤波估计法的陀螺漂移残差标准差小。
2)在谐波系数估计的收敛时间方面,递推最小二乘法比Kalman滤波收敛的快,但递推最小二乘的收敛过程对各向量的初值较敏感,数据需要预先处理后才能进入迭代运算,而Kalman滤波对系统初值无特殊要求。
3)统计检验表明,陀螺误差模型的谐波系数回归方程以及估计的各谐波系数是显著的。由此可以判断陀螺误差系数Dyz和Dzz显著,但是尚不能给出数值较小的Dxy、Dxz和Dy是否显著的结论。
当三浮陀螺进行伺服测试时,在模型及参数准确的前提下,用Kalman滤波的方法估计误差系数是一种更好的选择。需要注意的是,当测试陀螺长时间精度时,为了防止新量测值对估计值修正作用下降,陈旧量测值修正作用相对上升,可以根据最优算法结合实际情况采用渐消记忆或限定记忆的方法辨识误差模型。极轴伺服测试得到的陀螺某些误差系数数值较小,一些二次项也无法用统计检验进行显著性分析,建议对这些误差项在高g下进行辨识。
[1]胡恒章.陀螺仪漂移测试原理及其实验技术[M].北京:国防工业出版社,1981. HU Heng⁃zhang.Test theory and technology of gyro drift[M].Beijing:National Defense Industry Press,1981.
[2]王广雄.控制系统设计[M].北京:中国宇航出版社,1992. WANG Guang⁃xiong.Control system design[M].Beijing:China Aerospace Press,1992.
[3]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998. QIN Yong⁃yuan,ZHANG Hong⁃yue,WANG Shu⁃hua. Kalman filter and integrated navigation theory[M].Xi'an:Northwestern Polytechnical University Press,1998.
[4]魏宗康,夏刚,朱宗荣,等.陀螺仪漂移误差参数估计的方案设计[J].导航与控制,2003,2(1):59⁃62. WEI Zong⁃kang,XIA Gang,ZHU Zong⁃rong,et al.Cali⁃bration scheme of gyro's drift errors[J].Navigation and Control,2003,2(1):59⁃62.
[5]张克志,田蔚风,钱峰,等.静电陀螺静态漂移误差模型系数的UKF标定方法[J].上海交通大学学报,2008,42(8):1387⁃1391. ZHANG Ke⁃zhi,TIAN Wei⁃feng,QIAN Feng,et al.Un⁃scented Kalman filter calibration method of electrostatically suspended gyroscope drift[J].Journal of Shanghai Jiaotong University,2008,42(8):1387⁃1391.
[6]吴广玉.系统辨识与自适应控制(下)[M].哈尔滨:哈尔滨工业大学出版社,1987. WU Guang⁃yu.System identification and self⁃adaptation control(2nd)[M].Harbin:Harbin Institute of Technology Press,1987.
[7]安学彬,万彦辉.三浮陀螺仪随机漂移模型研究[J].压电与声光,2009,31(5):643⁃645. AN Xue⁃bin,WAN Yan⁃hui.Research on random drift model of three⁃floated gyro[J].Piezoelectrics&Acous⁃tooptics,2009,31(5):643⁃645.
[8]李璐,孙纯祥.三浮陀螺随机漂移数据建模[J].压电与声光,2011,33(3):378⁃381. LI Lu,SUN Chun⁃xiang.Modeling of random drift data of the liquid floated gyro[J].Piezoelectrics&Acoustooptics,2011,33(3):378⁃381.
[9]何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2015. HE Xiao⁃qun,LIU Wen⁃qing,Applied regression analysis[M].Beijing:China Renmin University Press,2015.
[10]刘建波,魏宗康.石英加速度计误差系数显著性分析[J].中国惯性技术学报,2011,19(5):615⁃620. LIU Jian⁃bo,WEI Zong⁃kang.Significance analysis of QFPA's error model's coefficients[J].Journal of Chinese Inertial Technology,2011,19(5):615⁃620.
[11]严恭敏,李四海,秦永元.惯性仪器测试与数据分析[M].北京:国防工业出版社,2015. YAN Gong⁃min,LI Si⁃hai,QIN Yong⁃yuan.Inertial de⁃vice test and data analysis[M].Beijing:National Defense Industry Press,2015.
Calibration of SDFG Coefficient Based on Servo Test
WANG Yong⁃tong,ZHU Zhi⁃gang,GUO Zong⁃ben,XU Chao
(Beijing Institute of Aerospace Control Devices,Beijing 100039)
When single⁃degree⁃of⁃freedom rate⁃integrating gyro(SDFG)in servo test,to calibrate the coefficient of SDFG whose axis of rotation is nominally parallel to the earth's polar axis,Kalman filter and recursive least⁃squares method were adap⁃ted in this paper.The data show that the Kalman filter method is efficient.Subsequently,the regression equation and coefficients were analyzed by statistical test,and the results verified that the calibrated coefficient Dvzand Dzzis creditable.
single⁃degree⁃of⁃freedom rate⁃integrating gyro;servo test;Kalman filter;error coefficient estimation; prominence analysis
U666.16+3
A
1674⁃5558(2017)05⁃01254
10.3969/j.issn.1674⁃5558.2017.01.018
王永彤,女,高级工程师,研究方向为导航、制导与控制。
2016⁃03⁃16
—— 对极轴(下)

