基于正反Kalman滤波的动基座重力仪数据处理方法

熊志明，郭 刚，李东明，罗 骋，李海兵

（北京航天控制仪器研究所，北京100039)

基于正反Kalman滤波的动基座重力仪数据处理方法

熊志明，郭 刚，李东明，罗 骋，李海兵

（北京航天控制仪器研究所，北京100039)

重力数据处理是动基座重力仪的核心技术，采用了一种基于正反Kalman滤波的数据处理方法提取重力异常值。以动基座重力仪（Sea and Air Gravity，SAG)为研究对象，根据系统参数推导了Kalman滤波方程，并运用正反Kalman滤波方法处理了SAG某飞行架次的数据。将提取的重力异常值与同机搭载飞行的俄罗斯高精度重力仪GT⁃1A的结果进行比对，试验结果表明，两者滤波结果差值的均方根误差要小于1mGal。

动基座重力仪；重力异常；重力数据处理；正反Kalman滤波

0 引言

航空重力测量是在机载重力和GPS组合系统下进行空中重力测量的技术，它是陆地重力和海洋重力测量的拓展和补充，也是重力测量的重要发展方向之一。基于测量速度快、覆盖范围大等优点，航空重力测量可用于大地水准面测定、无人区重力测量、远程武器发射区快速重力测量等方面。目前，航空重力测量技术在地球物理勘探方面得到广泛应用，服务领域涉及基础地质调查与研究、空间科学、石油、天然气及固体矿产资源勘探、大地测量等方面［1］。

重力数据处理对获取高精度重力异常值起到了重要作用。航空重力是在飞机上进行测量，飞机的高频振动将不可避免对重力仪测量数据和DGPS解算数据产生高频干扰影响，因此提取的重力异常初值也含有大量的高频噪声。为了得到有用的重力异常信号，需进行低通滤波消除高频干扰。本文围绕重力数据低通滤波处理这一核心技术展开工作。

目前数据低通滤波处理方法包括无限脉冲响应（Infinite Impulse Response，IIR)低通滤波方法、有限脉冲响应（Finite Impulse Response，FIR)低通滤波方法、RC滤波方法、高斯滤波方法、FFT滤波方法等。以上滤波处理方法都是基于非模型的低通滤波算法，容易导致滤波信号中重力异常信号的损失。因此，对于分辨率要求较高的地球物理勘探来说，需选择基于模型的Kalman滤波估计方法技术作进一步处理［11］，即对重力异常建模并通过Kalman滤波估计重力异常值。

本文在文献［9］和文献［13］的基础上对重力异常模型进行改进，用正反Kalman滤波方法处理SAG的数据，并与用标准离散Kalman滤波方法处理的结果进行对比。

1 SAG系统组成及数据处理流程

1．1 系统组成

SAG是基于捷联惯导的动基座重力仪，以捷联惯性导航为基础，结合差分GPS系统，可以实现动态重力测量。动基座重力测量系统功能组成如图1所示，分为载体、地面和离线处理工作站3个组成部分。

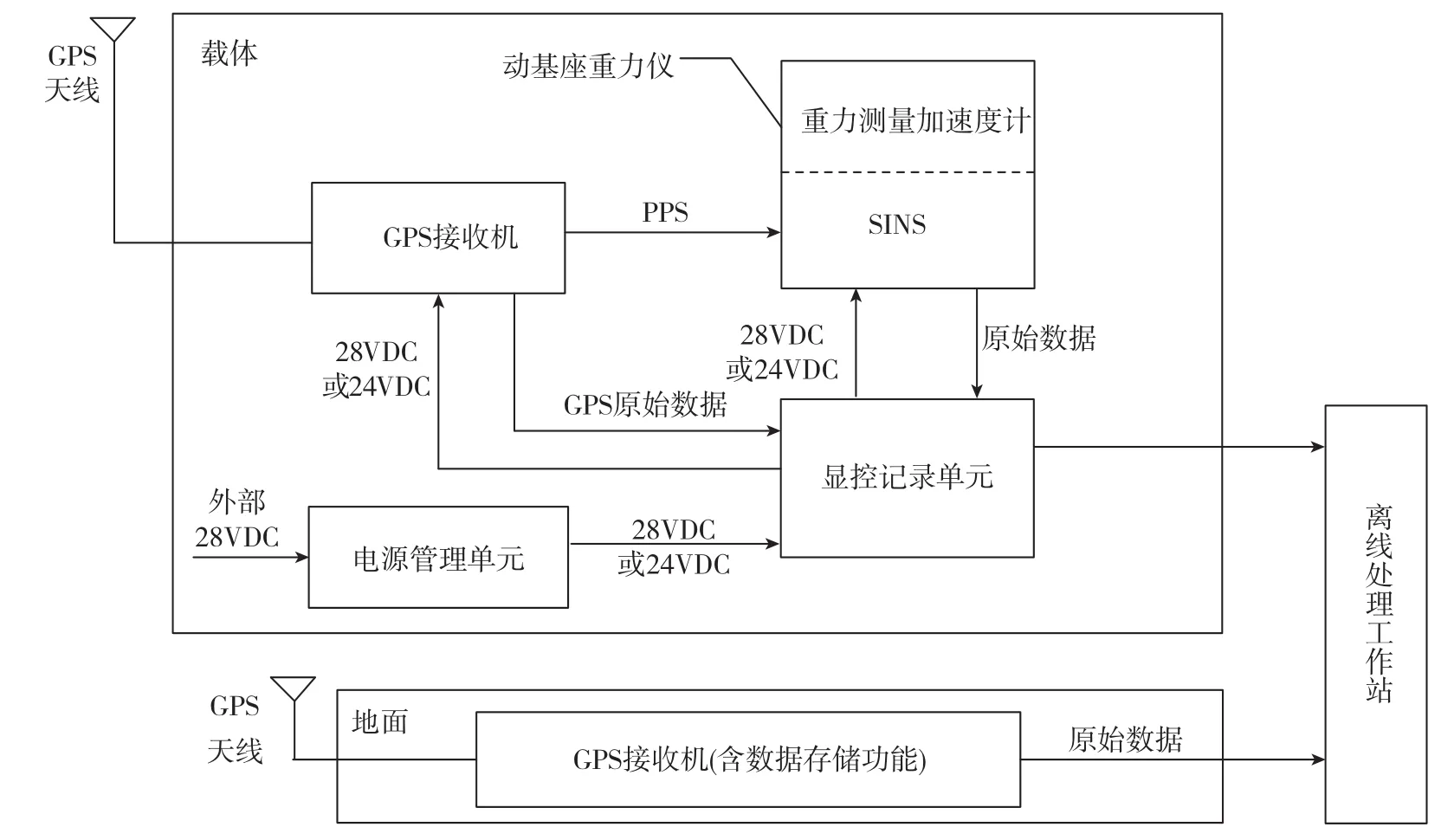
图1 动基座重力测量系统功能组成示意图Fig．1 Schematic diagram of moving base gravity system

载体部分，以动基座重力仪为核心单元，同时还包括由GPS天线和GPS接收机构成的差分GPS移动站、显控记录单元、电源管理单元。

地面部分，主要是由GPS天线和GPS接收机构成的差分GPS基站。

离线处理工作站部分，主要是对数据进行离线处理的计算机及程序软件。

SAG系统包括重力仪及后处理软件系统。重力仪如图2所示，主要包含惯性测量单元、GPS基站、数据采样记录仪、28V直流电源、不间断电源系统UPS、电源显示控制单元。其中，惯性测量单元如图3所示。

图2 重力仪Fig．2 Gravimeter

图3 惯性测量单元Fig．3 Inertial measurement unit

1．2 数据处理流程

数据处理流程图如图4所示，重力仪输出的数据通过记录仪存储，数据包括陀螺、加速度计的原始脉冲以及GPS原始数据。GPS原始数据经差分处理得到精确的位置和速度信息；陀螺和加速度计的原始脉冲经误差补偿后得到加速度和角速度，经捷联惯性导航得到位置、速度和姿态。将惯性导航的结果与GPS的速度和位置进行组合导航，来修正姿态信息得到导航系下的3个比力值。对重力异常进行建模后联立导航系下的比力值建立Kalman滤波方程，经正反Kalman滤波后得到精确的重力异常值。

由图4可以看出，数据处理流程先进行导航解算，再进行重力异常值的提取。导航解算处理包括误差补偿、捷联惯性解算、组合导航。重力异常提取是在导航解算的基础下进行，包括重力异常建模和Kalman滤波方程构建。

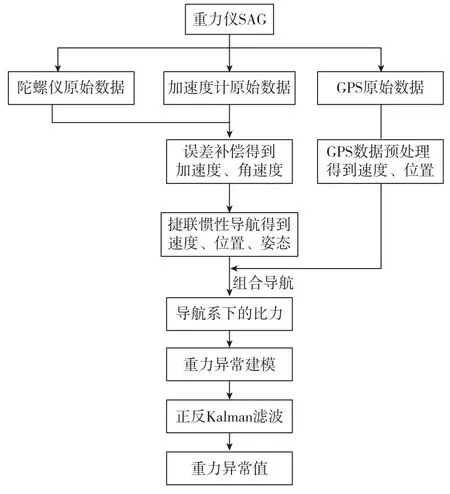
图4 重力数据处理流程Fig．4 Flow chart of gravity data processing

2 正反Kalman滤波与标准Kalman滤波比较

2．1 标准离散Kalman滤波

设离散线性系统的状态方程和观测方程分别为［12］：

其中，Xk为tk时刻的状态向量；ϕk，k-1为tk-1时刻至tk时刻的一步转移阵；Γk-1为系统噪声耦合矩阵；Zk为tk时刻的观测向量；Hk为量测阵；Vk为量测噪声序列；Wk为系统激励噪声序列。

Kalman滤波要求｛Wk｝和｛Vk｝是互不相关的零均值的白噪声序列，有：

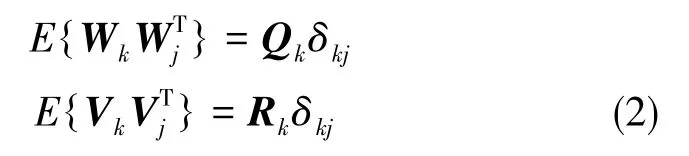
Qk和Rk分别为系统噪声和量测噪声的方差矩阵，在Kalman滤波中要求它们分别是已知值的非负定阵和正定阵。

离散Kalman滤波方程为：

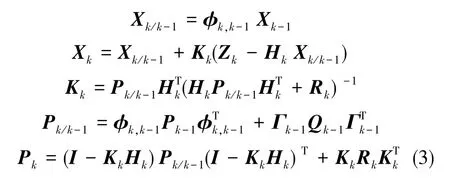
其中，Pk为估计误差方差阵，Kk为最优增益矩阵或者加权矩阵，Pk／k-1为一步预测均方误差，Xk／k-1为状态一步预测。

2．2 正反Kalman滤波器

正反Kalman滤波即将Kalman正向滤波以及Kalman反向滤波的结果进行某种形式的加权求和。将Kalman反向滤波过程k时刻所得的一步状态预测量、状态估计分别记为xf（k／k-1)、xf（k)，相应的误差协方差矩阵分别记为Pf（k／k-1)、Pf（k)。假设Kalman正向滤波产生的状态估计量的数据个数为n，那么Kalman反向滤波过程的一步状态预测量及其误差协方差矩阵初值记为xf（n／n-1)＝0，Pf（n／n-1)＝0。当k由n时刻反向变化为0时刻时，正反Kalman反向滤波的校正过程以及预测过程表达式如下所述。

正反Kalman反向滤波校正过程［9］如式（4)所示。

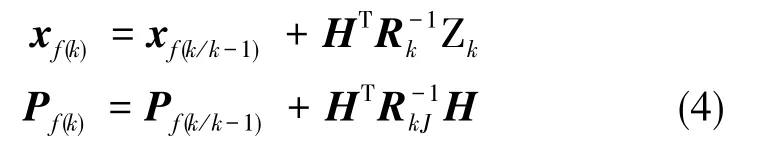
预测过程［9］如式（5)所示。

正反Kalman加权［9］如式（6)所示。

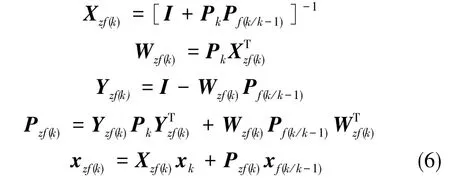
正反Kalman滤波的状态量是Kalman正向滤波的状态估计量xk与Kalman反向滤波的状态估计量xf（k／k-1)的加权求和，两者的权重分别为

2．3 正反Kalman滤波器的特点

标准离散Kalman滤波是正向Kalman滤波过程，一步状态估计量和观测量通过Kalman增益以及相应的误差协方差矩阵各自对状态估计量进行修正；正反Kalman滤波器在标准离散Kalman滤波器的基础上进行了一次反向滤波，并将两种结果进行加权求和，这样能充分使用标准离散Kalman滤波所产生的一步状态估计量、状态估计量及相应的误差协方差矩阵的信息，可以得到更优化的滤波结果。

3 重力异常建模

SAG是基于捷联惯导的动基座重力仪，原始输出量为陀螺仪在载体系下的角度增量和加速度计在载体系下的速度增量。经过SINS／DGPS组合导航滤波方法计算精确的导航系下的比力f′1、f′2、 f′3。但由于计算误差等因素影响，f′3与真值会有微小偏差，对其建立如下方程：

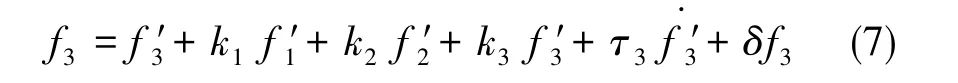
其中，k1、k2为姿态失准角，k3为标度因数误差，τ3为延时参数，δf3为重力噪声。航空重力标量测量的数学模型为：

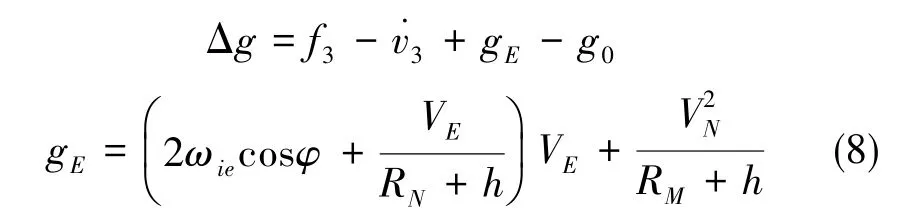
其中，g0为正常重力值，gE是由地球自转和载体相对地球运动引起的，称为厄特弗斯改正项。令：

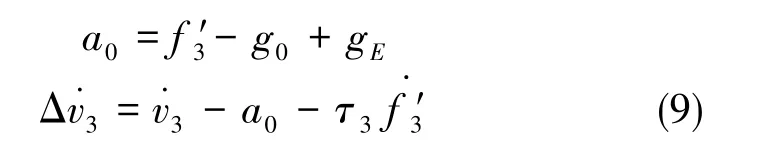
其中，v3为GPS测量的天向速度，Δv3为天向速度误差。将式（7)和式（9)代入式（8)中，得：

由此建立动基座重力仪的高度误差方程：

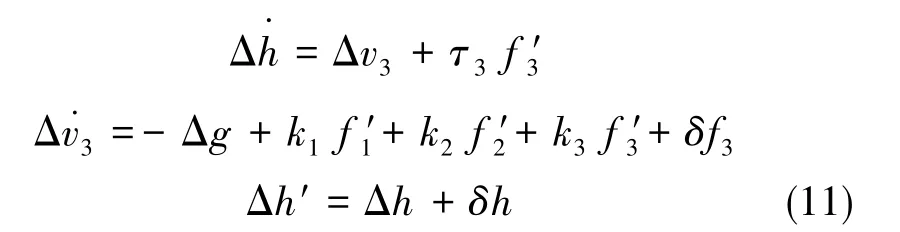
其中，Δh为高度差，为GPS测量的高度与IMU积分得到的高度差。Δh′的结果由式（12)得到：

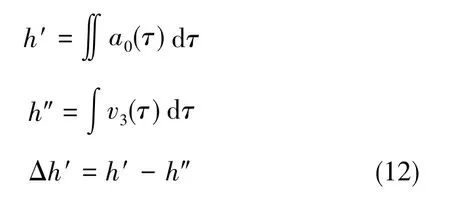
其中，h′为天向运动加速度a0经过二次积分得到，h″为对GPS天向速度v3积分得到。

重力异常是个随机过程，目前，通常采用高斯⁃马尔科夫随机过程对重力扰动进行建模，3阶高斯⁃马尔科夫过程的微分方程为［10］：

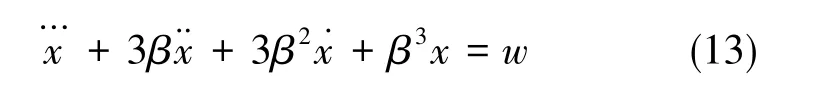
其中，β为相关参数，w为输入的白噪声。

根据式（13)，重力异常的模型可以写成如下形式：

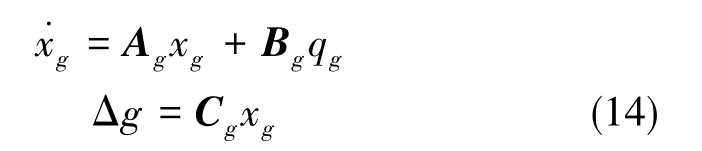
qg是方差强度为Qg的白噪声，Ag、Bg、Cg为常值矩阵。

式（14)结合动基座重力仪的高度误差方程，即可得到重力异常值估计的Kalman滤波方程：

式中，状态变量为x＝［xaxg］T，xa＝［Δv3Δh τ3k1k2k3］T，qf、qk、δh为白噪声。高度差Δh′为状态观测量。

4 飞行试验结果对比

采用上述重力异常模型，分别用标准Kalman滤波和正反Kalman滤波方法对SAG某次飞行试验数据进行了处理，本文给出了其中6条飞行测线处理结果，并将两种结果与同机飞行的GT重力仪结果进行对比。飞机平稳等高度飞行，飞行的平均高度为1500m，飞行平均速度为65m／s。飞行轨迹如图5所示。

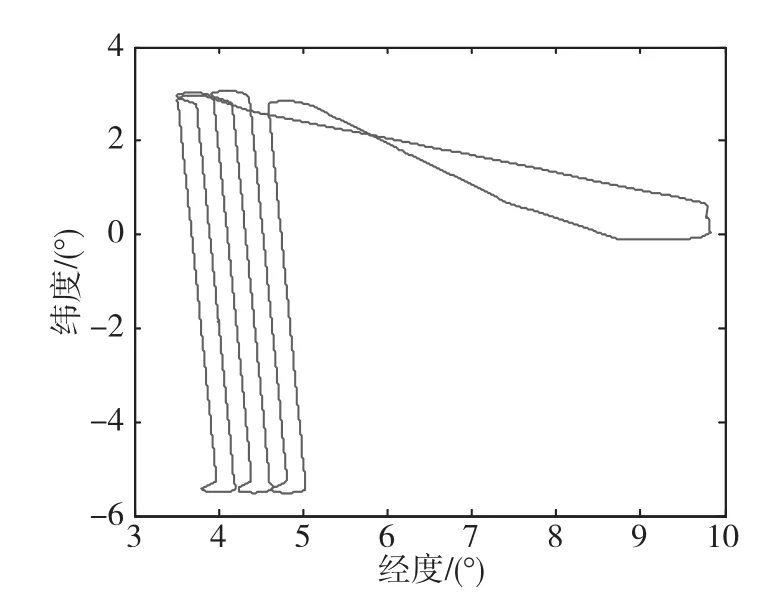
图5 飞行轨迹图Fig．5 Flight path

由图5可以看出，飞行轨迹为6条南北测线。从左至右6条测线分别为测线1至测线6。6条测线的对比曲线分别如图6～图11所示。

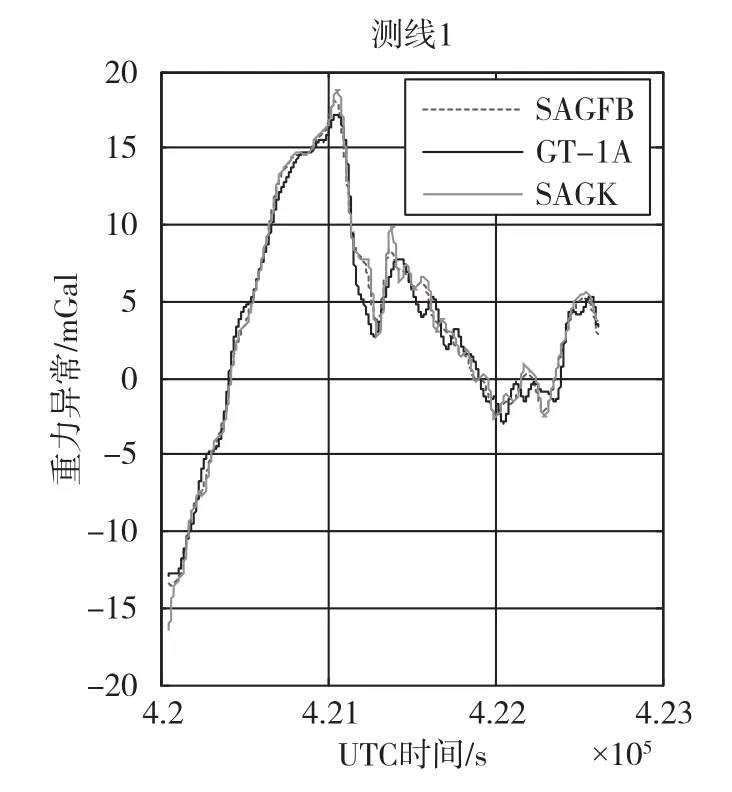
图6 测线1对比曲线Fig．6 Comparison of line 1

图7 测线2对比曲线Fig．7 Comparison of line 2

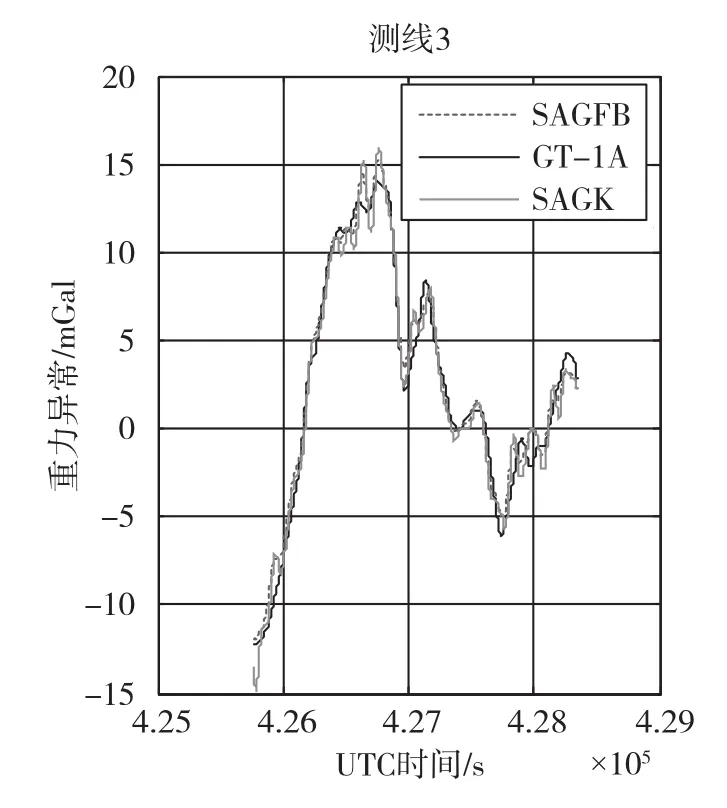
图8 测线3对比曲线Fig．8 Comparison of line 3

图6～图11中的虚线为采用本文的重力异常模型和正反Kalman滤波方法处理的SAG的重力异常曲线（SAGFB)；点线为用标准Kalman滤波方法处理SAG的重力异曲线（SAGK)；实线为GT⁃1A的重力异常曲线（GT⁃1A)；曲线的横坐标为UTC时间，单位为s；纵坐标为重力异常值，单位为mGal（10-5m／s2)。由曲线可以看出，两种Kalman滤波方法估计出来的SAG的重力异常曲线与GT⁃1A的重力异常曲线趋势基本一致。为了更好地比较两种滤波方法，本文统计了两种滤波结果与GT⁃1A结果的符合性精度，如表1所示。

图9 测线4对比曲线Fig．9 Comparison of line 4

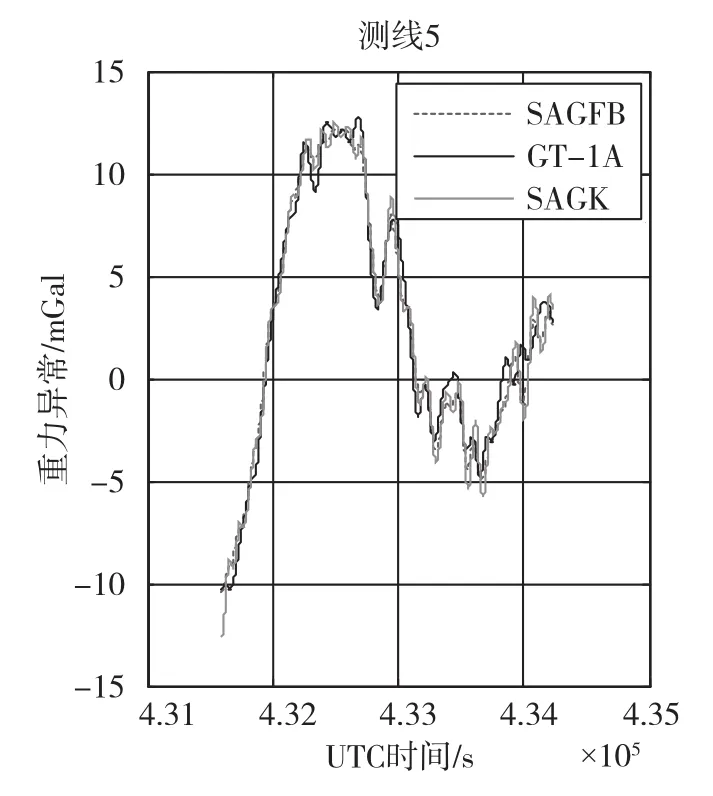
图10 测线5对比曲线Fig．10 Comparison of line 5

表1 SAG与GT⁃1A测量结果的符合性统计表Table 1 Statistical table of measuring result between SAG and GT⁃1A

表1以SAG与GT⁃1A在每条测线上所有测点的均方根误差来评价2套不同重力仪的符合性，并比较两种滤波方法的精度，测点的采样周期为2Hz。每条测线的测点数如表1中第6列所示，各条测线差值的均方根在表的第3列和第5列给出。由表1可以看出，用正反Kalman滤波方法处理的各条测线的差值均方根在1mGal以内，6条测线误差的均方根的平均值为0.9073mGal；用标准离散Kalman滤波方法处理的各条测线的差值均方根高于1mGal，均方根的平均值为1.1273mGal。由此看出，正反Kalman滤波的结果要好于标准离散Kalman滤波的结果。

每条测线的误差均值A计算公式如式（16)所示。

其中，n为测线的点个数，即表格第4列所示；x1、x2、…、xn为GT⁃1A处理的各个测点的重力异常值；y1、y2、…、yn为SAG处理的各个测点的重力异常值；a1、a2、…、an为两种仪器处理的各个测点的重力异常之差。

误差的均方根D的计算公式如式（17)所示。

5 结论

本文探讨了基于正反Kalman滤波的重力异常提取方法，采用该方法对动基座重力仪SAG实际飞行测量数据进行了处理，并与同机飞行的国外进口GT⁃1A重力仪结果进行了对比。根据SAG与GT⁃1A的符合性统计结果表明，本文的滤波方法获得的处理精度与GT⁃1A精度相当，能满足航空重力勘察测绘的要求。这验证了重力异常模型的合理性和正反Kalman滤波算法的实用性，也从侧面反映了SAG已达到国外进口产品同等精度。下一步研究的重点在于进一步优化重力异常模型，得到更精确的模型。

本次飞行试验得到了中国国土资源部物探遥感中心的大力帮助，在此表示诚挚的感谢。

［1］熊盛青，周锡华，郭志宏，等.航空重力勘探理论方法及应用［M］.北京：地质出版社，2010. XIONG Sheng⁃qing，ZHOU Xi⁃hua，GUO Zhi⁃hong，et al.Thoery，method and application of the airborne gravity prospecting［M］.Beijing：Geology Press，2010.

［2］郭志宏，罗锋，王明，等.航空重力数据无限脉冲相应低通数字滤波器设计与实验研究［J］.地球物理学报，2011，54（8）：2148⁃2153. GUO Zhi⁃hong，LUO Feng，WANG Ming，et al.The de⁃sign and experiment of IIR lowpass digital filters for air⁃borne gravity data［J］.Chinese Journal of Geophysics，2011，54（8）：2148⁃2153.

［3］蔡体菁，周薇，丁昊，等.航空重力数据与重力梯度信号处理［C］.惯性技术发展动态发展方向研讨会，2014：53⁃56. CAI Ti⁃jing，ZHOU Wei，DING Hao，et al.Data pro⁃cessing for airborne gravity and land gravity gradient［C］. Dynamic Development Direction Seminar of Inertial Tech⁃nology development，2014：53⁃56.

［4］田颜锋，李姗姗，刘晓刚，等.航空重力数据低通滤波处理及其功效分析［J］.大地测量与地球动力学，2009，29（6）：130⁃132. TIAN Yan⁃feng，LI Shan⁃shan，LIU Xiao⁃gang，et al. Low pass filter and its effect in data processing of aerial gravity measurements［J］.Journal of Geodesy and Geody⁃namics，2009，29（6）：130⁃132.

［5］郭志宏，罗锋，安战锋.航空重力数据窗函数法FIR低通数字滤波试验［J］.物探与化探，2007，31（6）：568⁃571. GUO Zhi⁃hong，LUO Feng，AN Zhan⁃feng.Experiment researches on FIR low pass digital filters based on window functions of airborne gravity data［J］.Geophysical And Geochemical Exploration，2007，31（6）：568⁃571.

［6］李宜龙，曾敏，孙科，等.航空重力测量中FIR滤波与高斯滤波的比较［J］.海洋测绘，2014，34（6）：40⁃42. LI Yi⁃long，ZENG Min，SUN Ke，et al.Comparison be⁃tween FIR filter and Gaussian filter in airborne gravity sur⁃veys［J］.Hydrographic Surveying and Charting，2014，34（6）：40⁃42.

［7］袁园.航空重力数据常用滤波方法对比研究［J］.吉林大学学报，2010，40（S1）：6⁃9＋38. YUAN Yuan.Comparative study of common filtering methods used in airborne gravity data［J］.Journal of Jilin University，2010，40（S1）：6⁃9＋38.

［8］孙中苗，夏哲仁.FIR低通差分器的设计及其在航空重力测量中的应用［J］.地球物理学报，2000，43（6）：850⁃855. SUN Zhong⁃miao，XIA Zhe⁃ren.Design of FIR lowpass differentiator and its applications in airborne gravimetry［J］. Chinese Journal of Geophysics，2000，43（6）：850⁃855.

［9］孟涛.卡尔曼滤波在航空重力数据处理中的应用研究［D］.东南大学，2012. MENG Tao.Kalman filter for airborne gravity data［D］. Southeast University，2012.

［10］Gelb A.Applied optimal estimation［M］.Cambridge，Massachusetts：MIT Press，1974.

［11］王静波，熊盛青，郭志宏，等.航空重力数据Kalman滤波平滑技术应用研究［J］.地球物理学进展，2012，27（4）：1717⁃1722. WANG Jing⁃bo，XIONG Sheng⁃qing，GUO Zhi⁃hong，et al.Kalman smoothing for airborne gravity data［J］.Pro⁃gress in Geophysics，2012，27（4）：1717⁃1722.

［12］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安：西北工业大学出版社，1998. QIN Yong⁃yuan，ZHANG Hong⁃yue，WANG Shu⁃hua.Kal⁃man filter and principal of integrated navigation［M］.Xi'an：North Western Polytechnical University Press，1998.

［13］王静波，熊盛青，郭志宏，等.航空重力异常估计方法研究［J］.物探与化探，2011，35（4）：493⁃498. WANG Jing⁃bo，XIONG Sheng⁃qing，GUO Zhi⁃hong，et al.Research on methods for estimating airborne gravity anomalies［J］.Geophysical＆Geochemical Exploration，2011，35（4）：493⁃498.

［14］Senobari M S.New results in airborne vector gravimetry using strapdown INS／DGPS［J］.Journal of Geodesy，2010，84（5）：277⁃291.

［15］李东明，郭刚，薛正兵，等.激光捷联惯导车载重力测量试验［J］.导航与控制，2013，12（4）：75⁃78. LI Dong⁃ming，GUO Gang，XUE Zheng⁃bing，et al. Gravimetry test of laser strapdown INS on ground⁃vehicle［J］.Navigation and Control，2013，12（4）：75⁃78.

［16］孙中苗，翟振和，李迎春.航空重力仪发展现状和趋势［J］.地球物理学进展，2013，28（2）：1⁃8. SUN Zhong⁃miao，ZHAI Zhen⁃he，LI Ying⁃chun.Status and development of airborne gravimeter［J］.Progress in Geophysics，2013，28（2）：1⁃8.

Gravity Data Processing Based on Forward and Backward Kalman Filter

XIONG Zhi⁃ming，GUO Gang，LI Dong⁃ming，LUO Cheng，LI Hai⁃bing
（Beijing Institute of Aerospace Control Devices，Beijing 100039)

Gravity data processing is the key technology of moving base gravimeter.A data processing method based on forward and backward Kalman filter was used to extract gravity anomaly.According to the system parameter of sea and air gravity（SAG)，Kalman filter equation was deduced and flight data of SAG was processed through forward and backward Kalman filter.It was shown that the root⁃mean⁃square error of the difference of gravity anomaly is lower than 1 mGal by comparing the gravity anomaly result of SAG with GT⁃1A which both been carried on the airplane.

moving base gravimeter;gravity anomaly;gravity data processing;forward and backward Kalman filter

P631.1＋25

A

1674⁃5558（2017)03⁃01232

10.3969／j.issn.1674⁃5558.2017.01.014

熊志明，男，硕士，研究方向为动基座重力测量系统。

2016⁃01⁃13

国家高技术研究发展（863)计划（编号：2011AA060506)；国家国际科技合作专项（编号：2014DFR80750)；航天科技集团公司九院创新基金项目（动基座重力测量系统，航空重磁一体化综合信息系统)