一种球面网壳型平台框架设计及仿真分析

黄云龙，魏宗康

（北京航天控制仪器研究所，北京100039)

一种球面网壳型平台框架设计及仿真分析

黄云龙，魏宗康

（北京航天控制仪器研究所，北京100039)

针对环形和球形惯性稳定平台框架的不足，提出一种球面网壳型惯性稳定平台框架设计。组合正12面体和正20面体并映射到球面上，接着一次细化得到一种由240个弧三角构成的球面网壳。然后通过PROE绘制网壳，确定框架及各部件的大小，并处理轴安装部位，得到一种对流和导热效果很好且等刚度的球面网壳型惯性稳定平台框架。最后通过ANSYS软件作静力学仿真与模态分析，验证结构具有足够的刚度与强度。

平台框架；球面网壳；静力学分析；模态分析

0 引言

平台式惯导系统通过加速计测量载体的视加速度，并通过安装在平台框架上的传感器取得载体相对台体的姿态信息，从而获取计算所需的导航参数［1⁃2］。良好的平台框架利于提升平台系统性能，提高测量精度，以实现精确导航；而理想的平台框架结构应具有足够的刚度和强度，易于实现热传导与热对流，建立良好的温度场，并具备良好的抗干扰性能。

就目前惯性稳定平台框架的发展来看，环形结构因其在3个轴向的转动惯量不一致，会明显地引入2阶非线性干扰力矩［3］；球形结构避免了2阶干扰，却因结构封闭而不利于热传导与热对流。为了吸纳这两种结构的优势，考虑对球形结构作镂空改进，提出一种球面网壳型惯性稳定平台框架设计。

1 球面网壳框架设计

三角形具有稳定性，而网壳结构又需要分布整个球面，因而考虑使用一种仅由弧三角构成的球面网壳；从结构对称性出发，可将正多面体映射到球面上［4］，再展开细化设计。本设计使用所有弧边皆为短程线，即球面上任意两点和球心所构成平面与球面相交部分所对应的一段短弧［5］；简称由几条弧边所构成的多边形为弧多边形；简称所有弧边等长的弧多边形为等弧多边形。

1．1 组合体映射结构

在直角坐标系下，取一个单位正12面体（各顶点到体心距离为1)，将它映射到单位球面上，得到12个相等的等弧五边形所围成结构。按照表1所示选取正12面体的20个顶点坐标并对其按1～20编号，12个等弧五边形的信息由表2给出，每个等弧五边形由顶点1到顶点5依次连接并闭合得到。

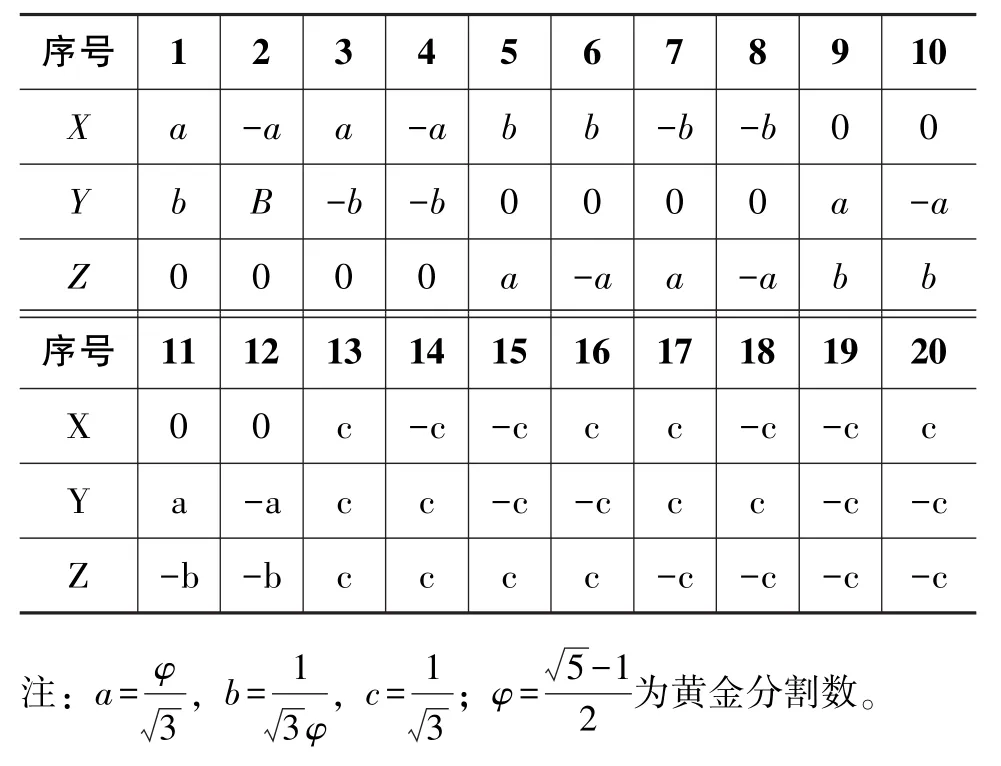
表1 20个顶点坐标分布Table 1 Position of 20 vertexes

表2 12个等弧五边形Table 2 12 equal bow pentagons

正12面体的映射结果如图1所示，它的所有

图1 正12面体映射结构Fig．1 Reflect the pentagonal dodecahedron

图2 组合体映射结构Fig．2 Reflect the combinant

这12个等弧五边形的几何中心构成一个正20面体，图2实际由单位正12面体和单位正20面体对称组合并映射球面得到。该组合体映射结构共60面相等的弧三角形；每个弧三角形有2条弧边等长，剩余1条弧长也与之相近。

1．2 细化组合体

对组合体的每个弧三角形进行截半细化：取3条弧边中点，两两生成新弧边，将1个弧三角形细分为4个弧三角形。经过细分，结构共有4种长度的弧边，依次为0.3649、0.3262、0.3420和弧长相等。使用式（1)，可求取每个等弧五边形所对应正五边形的几何中心W；再用式（2)，可得到等弧五边形的几何中心N；从N到对应5个顶点作新弧边，得到图2所示结构。0.3789，所有弧长接近；共有3种弧三角形，但因所有弧长接近，所有弧三角形非常近似。

在结构体XOY、YOZ及ZOX面上，分别有2条（1组)长弧对称分布，每组长弧中点依次为球面网壳与Y轴、Z轴、X轴的交点。每条长弧由6条短弧相连而成。最终细分结构及3组长弧分布，如图3所示。

图3 最终结构及长弧分布Fig．3 Final structure with its long bows

1．3 PROE模型

取X轴、Y轴与球面网壳的相交部分为轴安装部位，设置轴孔；取YOZ面为剖面，将球面网壳分割。兼顾系统小型化应用需求与结构的稳定性，球体Z轴方向两端最大距离取250.88mm；X轴、Y轴方向，经轴端处理，两端最大距离都变为229.79mm；每条弧边取6mm粗；轴端附近作必要实面化处理；同时加粗安装面YOZ的圆环边，可得到一种球面网壳型框架，如图4所示。其中Y轴方向安装内部机构整体的旋转轴，可通过剖面YOZ打开安装；X轴方向安装此框架及其内部机构整体围绕外围机构旋转的旋转轴。

图4 一种球面网壳型框架示意图Fig．4 Sketch of spherical net shell style frame

2 仿真与分析

2．1 有限元模型

将PROE模型导入ANSYS后，选取铝合金为材料，再进行网格化分。通过权衡精度和执行效率（内存)，框架整体采用自动方式划分网格，根据曲率法确定网格大小，并取网格相关度为20，关联中心取为精细。最终得到网格节点数目239818个，网格单元数目134358个。框架有限元模型如图5所示。

图5 框架有限元模型Fig．5 FEM model of the frame

2．2 静力学分析

不考虑质量、阻尼等惯性因素的影响时，可应用ANSYS线性静态结构模块，计算在固定不变的载荷作用下结构的效应［6］。

以很大的加速度作变速运动时，框架的2对端口会通过X向、Y向2根旋转轴固定，而其最主要冲击来自于大过载。为了检验该框架能否承受得住如此大的冲击，定义3种工况并进行3组仿真。设置边界条件为4个端口面固定，然后在每组仿真中分别取X、Y、Z的正方向施加大小为30g的过载，运行得出3种工况下的形变云图和应变云图。其中，在X正方向上施加30g过载时，施加载荷与约束的情况，如图6所示。3种工况下的形变与应变云图，如图7、图8和图9所示。云图以夸张方式给出变形趋势和应变大小，因此要依照仿真数值结果对具体形变与应变作定量分析。

图6 X向载荷与约束Fig．6 Constraints and load of X direction

图7 X向加载30g时静力学分析Fig．7 Static structure analysis of X direction loading 30g acceleration

图8 Y向加载30g时静力学分析Fig．8 Static structure analysis of Y direction loading 30g acceleration

图9 Z向加载30g时静力学分析Fig．9 Static structure analysis of Z direction loading 30g acceleration

表3对3种工况下的结果进行了统计。不难发现，结构在X正方向上承受30g载荷作用时，最大位移与最大等效应力同时达到3种工况的最高值。此时，结构整体的最大变形仅为0.0812μm，相对整体结构小到可以忽略；最大等效应力为0.2037MPa，比铝合金的屈服刚度280MPa小了4个量级；很明显，该结构的刚度与强度足以支持其作大过载加速运动。

表3 工况为30g过载时分析结果比较Table 3 Results compare of loading 30g acceleration

2．3 模态分析

模态是机械机构的固有振动特性，每个模态具有特定的固有频率、阻尼比和模态振型。模态分析即自由振动分析，是系统辨识方法在工程振动领域中的应用，其最终目标是识别系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报、结构动力特性的优化设计提供依据［6］。

应用ANSYS模态分析模块，考虑应力效应的影响，得到框架前10阶主模态的固有频率和模态振型描述如表4所示。结构对称，使结果总出现两两非常接近的固有频率，而它们所对应的振型描述是相同的。

表4 前10阶主模态Table 4 Former 10 main modals

模态分析还显示，在各模态下，4个轴端经固定和实面化处理，结构相当稳定；而网壳化及剖面安装环部位相对容易出现谐振变形，但在静力学分析中明显看到，结构具有足够的刚度与强度，最大等效应力更是比铝合金的屈服刚度小了4个量级，所以由此估计，谐振产生的变形也不会非常大。其中，前两阶主模态所对应的振型云图，如图10所示。

图10 前2阶主模态振型Fig．10 Former 2 main modals vibration style

3 结论

本文研究一种球面网壳型惯性稳定平台框架。从两种正多面体的组合着手，将其映射到球面进行细化设计，再通过PROE绘制和处理，最终设计出一种镂空、对称且美观的球面网壳型框架。该结构在各转轴的转动惯量大小接近，使之能有效地减小2阶非线性干扰力矩，从而更有效地抗干扰；该结构镂空，使之更易于实现热传导和热对流，以建立良好的温度场。通过ANSYS仿真，还验证该框架具有足够的刚度与强度。但实际应用与仿真必然存在差异，在使用该框架结构实现平台系统的过程中，可作进一步的动力学仿真与测试，不断改进结构，以达到提高整个平台系统性能的目的。

［1］以光衢，王惠南，郭富强，等.惯性导航原理［M］.北京：航空工业出版社，1987. YI Guang⁃qu，WANG Hui⁃nan，GUO Fu⁃qiang，et al.In⁃itial navigation principle［M］.Beijing：Aircraft Industry Press，1987.

［2］秦永元.惯性导航［M］.北京：科学出版社，2007. QIN Yong⁃yuan.Initial navigation［M］.Beijing：Science Press，2007.

［3］陆元九.惯性器件（下)［M］.北京：中国宇航出版社，2009. LU Yuan⁃jiu.Initial device（2rd)［M］.Beijing：China Aer⁃ospace Press，2009.

［4］赵学胜.基于QTM的球面Voronoi数据模型［M］.北京：测绘出版社，2004. ZHAO Xue⁃sheng.Spherical Voronoi data modeling based on QTM［M］.Beijing：Surving and Mapping Press，2004.

［5］Randall D A，Ringler T D，Heikes R P，et al.Climate modeling with spherical geodesic grids［J］.Computing in Science and Engineering，2002，4（5)：32⁃40

［6］凌桂龙，丁金滨.Ansys Workben 13.0从入门到精通［M］.北京：清华大学出版社，2012. LING Gui⁃long，DING Jin⁃bin.Ansys Workbench 13.0 from primer to master［M］.Beijing：Tsinghua University Press，2012.

Design and Simulation Analysis of Spherical Net Shell Style Platform Frames

HUANG Yun⁃long，WEI Zong⁃kang
（Beijing Institute of Aerospace Control Devices，Beijing 100039)

Considering the defaults of annular and spherical initial stable platform frames，the concept of spherical net shell style initial stable platform frame was put forward.The design firstly combined a pentagonal dodecahedron and a regular icosahedron in a symmetrical way，and then reflected the combinant onto a spherical surface.After that，the struc⁃ture was subdivided into a kind of spherical net shell with 240 bow triangles.Meanwhile，the final net shell was generated via PROE，the size of the frame and its components was chosen，and the positions of axles'installation were carefully modi⁃fied.Finally we got a spherical net shell style initial stable platform frame with merits of good convection，perfect heat con⁃duction and equal stiffness.Moreover，static structure analysis and modal analysis of the structure were carried out via AN⁃SYS，proving its wonderful stiffness and strength.

platform frame;spherical net shell;static structure analysis;modal analysis

U666.1

A

1674⁃5558（2017)01⁃01225

10.3969／j.issn.1674⁃5558.2017.01.006

黄云龙，男，硕士，导航、制导与控制专业，研究方向为平台系统设计。

2016⁃01⁃05