短纤维增强橡胶材料隔层的强度与失效分析

刘沙石,侯 晓,郜 捷

(中国航天科技集团公司四院四十一所,西安 710025)

短纤维增强橡胶材料隔层的强度与失效分析

刘沙石,侯 晓,郜 捷

(中国航天科技集团公司四院四十一所,西安 710025)

对短切芳纶纤维EPDM材料试件进行了拉伸试验，利用数字图像分析法处理得到了准确的材料应力应变数据。根据火箭发动机柔性隔层的结构特点，用ABAQUS有限元分析软件建立了柔性隔层的有限元模型，利用轴对称结构大大简化了计算量。通过ABAQUS对拉伸试验数据进行拟合，得到了较为准确的超弹性本构模型，并通过此模型对隔层工作情况进行模拟，得到了隔层的实际应变情况。结果表明，当前工况下柔性隔层受载未超出材料强度极限，且尚具有较高的安全裕度，现有的安全判据是不可用的。改变壳体刚度、隔层与药住间隙计算其应变结果，并综合对比之前的结果，提出了有效的降低隔层应变方法，为隔层的优化提供了依据。

脉冲发动机；隔层；短切芳纶纤维EPDM材料；超弹性

0 引言

采用脉冲发动机的导弹具有高速、远射程、高命中率和较轻的系统结构质量特点，并具备优越的机动性能。在双脉冲发动机中，两个串联药柱由阻燃剂或隔板/隔层间隔开，隔板/隔层在二次点火火箭发动机中起着分隔燃烧室的作用。在第一级发动机工作时，隔板/隔层除了起到隔离高温燃气的隔热作用，还要作为承受一级发动机内压载荷的结构件使用。一脉冲工作时，隔层受到高温高压燃气的作用，发生较大的变形，有可能导致其结构失效而使二脉冲提前工作，燃烧室内压强快速升高，超过壳体的爆破压强进而导致发动机工作失利。因此，选择合适的隔离方案十分重要的。

目前，常用的隔板/隔层主要有陶瓷隔板、金属膜片隔层以及橡胶类材料的软质隔层。软质隔层体积小，质量轻，可与发动机装药、点火器一体化设计，是一种较好的隔离方案[1]。国内外有关隔层方面的有限元计算大多采用线弹性模型。文献[1]分析了金属膜片式隔板的受力情况；文献[2-3]对陶瓷隔板进行了有限元分析与优化设计；文献[4]分析了金属膜片式隔舱的动态破坏过程；文献[5]对预紧力对陶瓷隔板的作用进行了深入探讨。根据隔层特点，这些计算全部都采用了线弹性模型，得到了较为准确的结果。

本文所研究的隔层是一种软质隔层，主要由短纤维增强橡胶材料构成，基体为橡胶材料，与橡胶有着相似的力学性能，采用超弹性模型应能更准确的模拟其力学特性。国内外已经建立了很多超弹性本构模型用于描述弹性材料的力学行为，如Neo-Hookean 模型，Mooney-Rivlin模型、Yeoh模型、Ogden模型等[6]。本文计算基于Mooney-Rivlin和Ogden本构模型。Mooney-rivlin模型参数简单，计算量小，能较好地模拟超弹性材料在150%内的变形[7]；而Ogden模型在模拟大变形问题时具有较高的精度。这2种模型在一些橡胶或者类似的超弹性结构的计算中已经被广泛运用，但很少用于与多脉冲火箭发动机隔层有关的计算。

本文以单向拉伸试验为基础，采用超弹性本构模型对其工作状态下的受力情况进行数值模拟，结合隔层材料的破坏性能进行失效评估，并指出隔层结构的优化方向。

1 橡胶本构理论

大变形和高弹性是橡胶的基本力学特性和显著特点。对于这一特性的本构描述是讨论橡胶粘弹性、mullins效应、payne效应的基础。在连续介质力学中，弹性材料应该具有如下特性：

(1)施加一定的载荷，变形瞬时发生，反之亦然；

(2)载荷卸除后，材料完全回复到初始状态；

(3)应力和应变之间存在一一对应关系；

(4)存在一个应变能函数W(E,T)，应力可从应变能函数求偏导得出：

(1)

式中E和C分别为Green应变和右Cauchy-Green变形张量；T为温度。

特性4又称为超弹性，拥有特性4的材料称之为超弹性材料[8]。

本文计算的隔层主要由橡胶与短切芳纶纤维构成，其在加载过程中具有复合大变形、高弹性的性质。而根据实际情况，卸载并不是发动机隔层研究的重点。因此，运用超弹性模型来模拟隔层本构关系是有依据的。

1.1 Mooney-Rivlin模型

Mooney-Rivlin模型由于结构简单，在超弹性本构计算中被广泛应用，其应变能函数如下：

(2)

式中 N、C、d为材料常数，由材料试验确定；J为体积率，橡胶是不可压缩的，故取J=1。

通过应变能函数对主伸长比λ求导，并根据不可压缩材料单轴拉伸条件可得

(3)

式中t为单轴拉伸应力；λ为主伸长比。

(4)

这就是典型的Mooney-Rivlin公式。

1.2 Ogden模型

1972年Ogden提出了主伸长比λi作为应变能函数自变量的新的应变能函数。

Ogden应变能函数定义为

(5)

式中μn和αn为材料常数；K为初始体积模量。

通过应变能函数对主伸长比求导，并根据不可压缩材料单轴拉伸条件可得

(6)

进一步可得基于OGDEN模型的的单轴拉伸应力表达式为

(7)

2 标准试件试验及材料参数确定

试件采用哑铃状试样：试件狭窄部分的标准厚度为 2.0 mm，长度为25.0 mm。试件基本尺寸如图所示。

拉伸试验采用的实验设备为Z005电子材料万能试验机。

为尽可能模拟发动机工作过程中内压载荷作用下的应变率，采用500 mm/min的拉伸速率进行单向拉伸，连续监测力和位移、应力和应变的变化值，并通过整理分析，得到相关的单轴拉伸实验数据如图2所示。

根据拉伸实验所得数据，通过Abaqus软件拟合本构特性参数如表1、表2所示。

通过Abaqus拟合的超弹性本构模型力与位移曲线如图3所示。

C10C01D16．6488-18．69970

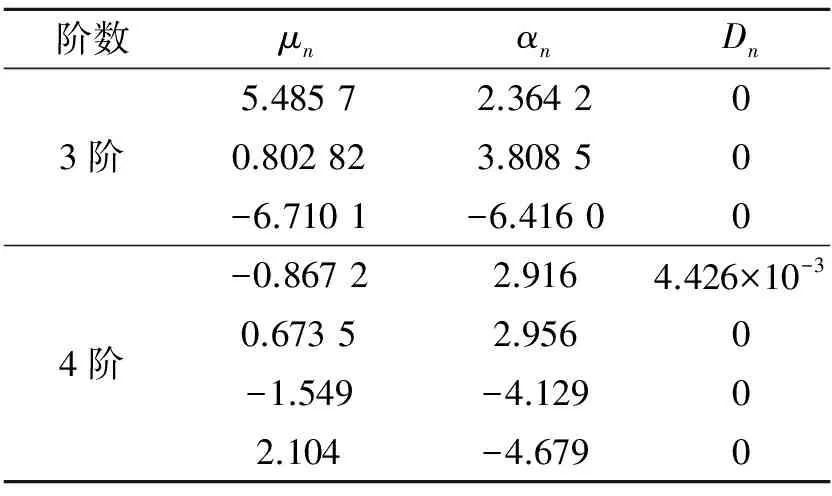
表 2 Ogden模型参数

由图3可看出，Mooney-Rivilin 模型由于参数过于简单，在模拟大变形问题时不能十分准确的反映材料性能；而Ogden模型与材料拉伸曲线在低应力时贴合良好，显然Ogden模型比Mooney-Rivlin模型更能准确反映隔层弹性材料性能。且随着参数数量的提升，4阶Ogden模型比3阶模型具有更高的精度。本文中采用4阶Ogden模型进行隔层结构的有限元分析。

3 计算实例

3.1 有限元分析前处理

为了简化计算，提高计算速度与精度，本次计算仅建立二脉冲发动机模型。发动机为轴对称模型，整个模型由隔层、药柱和壳体构成，其中隔层与药柱间存在一定的间隙。研究重点是隔层结构，在生成网格时局部细化。对药柱和壳体进行一体化布尔运算，采用轴对称缩减积分网格CAX4R。为了减轻沙漏效应，对隔层采用轴对称杂交缩减积分网格CAX4HR，开启沙漏控制增强开关。

发动机轴对称模型如图4所示，发动机半径为R，总长度为2.5R，隔层厚度为0.04R。

在发动机工作工程中，隔层受到一脉冲高温高压燃气作用，容易发现较大变形。由于两端受到壳体的限制，隔层中部理论上应承受较大的环向与径向应变，而轴向应变对隔层的影响相对较小。通过初步计算也认为隔层中部承受了较大的应变，这也与发动机实际失效情况相符。

在隔层中部选取图中A点为重点关注部位，因此在有限元分析过程中，对该部位进行网格细化。

药柱与隔层存在一定的摩擦系数，本次计算中对隔层与药柱接触处设定了0.4的摩擦系数。前裙施加固定约束，对隔层与壳体粘接处施加绑定约束。在分析过程中对隔层施加法向的压力，在1s内先施加一个较小的载荷，让隔层和药柱建立平稳接触。加载曲线如图5所示。

3.2 基于Ogden模型的超弹性有限元分析结果

取壳体刚度为200 GPa，有限元分析得到的隔层整体环向应变云图见图6，关键部位A点的环向应变见图7，A点环向应变随时间变化曲线见图8，加载结束后A点最终的应力应变值见表3。

参数环向径向轴向应力/MPa9109．16应变/%27．3271．9

A点的Von-Mises应变为31.7%。

为了分析壳体刚度、隔层与药柱之间间隙对隔层应变的影响，为隔层优化提供依据，改变了上述条件，进行了相同载荷下的计算，提取A点Mises应变结果见表4。其中壳体刚度变化通过改变其模量来实现。

综上所述可知：

(1)整个结构在受压过程中，由于结构模型限制，隔层在轴向、径向拉伸应变较小：径向方向上隔层与药柱相互挤压，主要受压缩应变，A点的压缩应变达到了25%；轴向方向上由于壳体变形，隔层两端受到了一定程度的拉伸应变，但是A点处拉伸应变接近于0。主要的拉伸应变出现在环向方向，在A点处达到了27.34%，这与发动机实际工作结果相符。

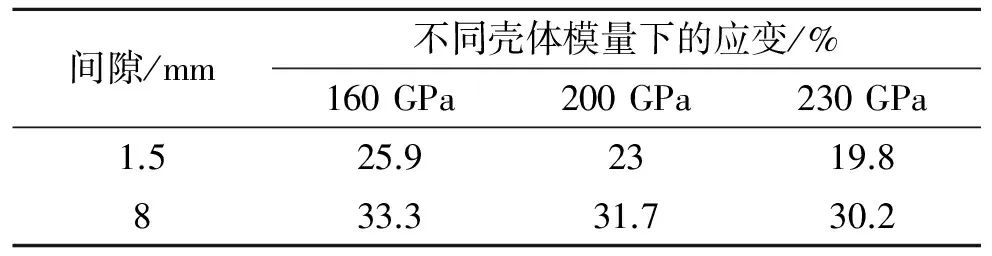
表 4 A点不同条件下隔层的Mises应变值

(2)整个发动机尤其是药柱与隔层具有较大径向位移，最大位移达到了14.8 mm，这是一个典型的大变形小应变问题。

(3)监测A点的环向应变历史输出变量，并同时监测相同轴向坐标上的药柱内侧、壳体环向应变历史输出变量，可发现存在一定的迟滞效应。超弹性隔层在受载后很快发生应变，之后与药柱发生接触，并由于药柱内孔扩张而使其应变进一步增大。壳体由于刚度较大所以应变较小。整个应变提高过程与加载曲线相符。当载荷升高速率加快时，应变提升也随之加快。径向位移历史输出变量也有着相类似的性质。

(4)4阶Ogden模型准确模拟了隔层工作情况，计算结果与实际工作过程基本相符，但最大应变远没有达到柔性隔层材料300%～600%的极限延伸率，说明隔层在达到强度极限之前就已经失效。现有的根据隔层强度极限得到的安全判据是不适用的。

(5)本文中的隔层材料为短切纤维增强的橡胶材料，纤维与橡胶基体之间存在着粘接面。当拉伸应变达到一定水平时，橡胶基体与填料间出现微裂纹与微孔洞；随着隔层应变的进一步增大，微裂纹与微孔洞逐渐发展为宏观裂纹，并在载荷作用下进一步扩展，最终导致结构失效。

(6)由表4看出，壳体刚度、隔层与药柱间隙对隔层应变均有显著影响，通过分析发现：增大壳体刚度与减小药柱与隔层间间隙均可使应变减小；当间隙较小时，刚度对应变的影响较为明显。

4 结论

(1)通过Mooney-Rivlin模型和不同阶数的Ogden模型对发动机隔层拉伸参数进行模拟，发现在大变形条件下，高阶的Ogden模型能更准确的拟合材料性质。

(2)通过对发动机实际工况进行有限元分析，认为发动机正常工况下隔层应变情况未超出材料极限延伸率，略微超过了材料的屈服应变。

(3)隔层应变远小于材料的极限延伸率之前就已经失效，表明现有的以最大延伸率作为材料承载极限的安全判据是不适用的。

(4)分析不同条件下隔层的应变变化情况，发现增大壳体刚度与减小药柱与隔层间间隙均可使应变减小；当间隙较小时，刚度对应变的影响较为明显。

(5)对隔层的优化应考虑在合理范围内增大壳体刚度和减小药柱与隔层之间的间隙。

[1] 刘世东,张辉,杨小良.脉冲发动机级间隔离技术研究[J].航空兵器,2011(4):55-57.

[2] 王长辉,刘亚冰,林震,等.脉冲发动机陶瓷隔板的设计和试验研究[J].固体火箭技术,2010,33(3):327-331.

[3] 高美艳,周紫光,方继明,等.陶瓷隔板的有限元分析及优化设计[C]//首届全国航空航天领域中的力学问题学术研讨会论文集(下册),北京航空航天大学,2004.

[4] 王春光,任全彬,田维平,等.脉冲发动机中金属膜片式隔舱动态破坏过程研究[J].固体火箭技术,2013,36(1):22-26.

[5] 刘亚冰,王长辉,刘宇,等.双脉冲固体发动机隔板预紧载荷数值分析[J].固体火箭技术,2010,33 (5):573-577.

[6] 谢志民,王友善,万志敏,等.热老化的填充橡胶本构关系[J].哈尔滨工业大学学报,2008,40 (9):1404-1407.

[7] 特雷劳尔.LRC.橡胶弹性物理力学[M].王梦蛟,王培国,薛广智,译.北京:化学工业出版社,1982:179-192.

[8] Guo Z,Sluys L J.Constitutive modelling of hyper-elastic rubber like material[J].HERON,2008,53:109-132.

(编辑：吕耀辉)

Strength and invalidation analysis of elastomeric barrier reinforced by short-staple fiber

LIU Sha-shi,HOU Xiao,GAO Jie

(The 41st Institute,The Fourth Academy of CASC,Xi'an 710025,China)

An uniaxial tensile test of the EPDM material reinforced by short-staple fiber was performed.Digital-image method was used to process the test data and obtain the accurate material stress-strain curve.According to the structure characteristics of elastomeric barrier in rocket engine,the finite element model of the barrier was established by finite element analysis software ABAQUS,the calculation was greatly simplified by using the axisymmetric structure.By fitting the tensile test data with ABAQUS,an accurate model of the hyperlasticity was obtained.The model was used to simulate the working situation of the barrier and the actual strain of interlayer was obtained.The result shows that under the working situation,the loading on the barrier does not exceed the strength limit of the material,and still has a high degree of safety,hence the current safety criterion is unavailable.The strain of barrier was calculated while changing the stiffness and the gap between barrier and grain.Comparing with the results before,the methods is put forward to reduce the barrier strain,and a method which can reduce the barrier strain effectively was put forward,which provide the basis for the optimization of the barrier.

pulse solid rocket motor;elastomeric barrier;EPDM material;hyperlasticity

2015-11-24；

2016-01-17。

刘沙石(1991—)，男，硕士，研究方向为多脉冲固体火箭发动机。E-mail：fishoohy@163.com

V255

A

1006-2793(2017)01-0100-05

10.7673/j.issn.1006-2793.2017.01.018