基于控制延时补偿的LLCL有源电力滤波器动态性能研究

（国网湖北省电力公司宜昌供电公司）

基于控制延时补偿的LLCL有源电力滤波器动态性能研究

陈 晗

（国网湖北省电力公司宜昌供电公司）

基于LLCL高阶滤波的有源电力滤波器（APF）可以更好地抑制PWM调制时产生的开关次高频谐波，但谐波电流跟踪控制在动态响应方面不可避免地存在延时，对谐波补偿效果带来一定影响。本文在研究谐波补偿电流跟踪控制器参数变化对系统稳态误差以及动态响应影响的基础上，针对延时对APF补偿效果的影响进行了理论分析，提出了一种利用补偿器来补偿延时和衰减系统高频分量的方法。最后通过仿真和实验验证所提控制方法能稳定、迅速而有效地响应谐波补偿。

有源电力滤波器；LLCL；延时补偿；动态响应

0 引言

APF作为进行动态谐波治理的高效装置，是未来谐波治理技术的发展方向。它克服了传统无源LC滤波器仅吸收固定频率的谐波，且容易过载等缺点[1-3]。为了减少在开关频率处产生的谐振电流，在传统的LCL滤波器中的滤波电容支路中加入了一个电感支路，形成了LLCL滤波器。LLCL滤波器衰减开关频率处的各电流谐波的能力要优于传统的LCL滤波器，能够减少电感装置的体积和重量，加速动态响应时间、提高特征谐振频率点，有利于APF的控制[4-5]。

一般认为APF可以克服无源滤波器的谐波放大问题，但是前提条件是补偿电流能对快速变化的谐波电流进行真正意义上的实时补偿。然而实际上，目前APF多采用数字化控制器实现，从谐波检测到补偿电流输出中的各个环节不可避免地存在延时，不可能做到严格意义上的实时补偿，即应该补偿的电流与APF输出的补偿电流不是同一时刻。目前对有源滤波技术的研究主要是集中在新拓扑结构和先进的控制算法方面，但是对延时给整个滤波系统造成的影响则少有涉及，虽然延时时间很短（一个到几个采样周期）[6-9]，但却严重影响了有源滤波器的补偿性能。因此，对控制延时及其补偿方法的研究是十分必要和有意义的。

本文采用基于LLCL滤波器的APF，对拓扑结构和数学模型进行分析，然后对基于LLCL滤波器的并联型APF产生延时的原因进行分析，并且分析了延时对APF谐波补偿的影响，最后将加入补偿环节后的重复学习控制运用于APF之中，通过仿真和实验验证了该方法的可行性。

1 主电路结构及数学模型

1.1 基于LLCL滤波的并联型APF电路结构和数学模型

图1是基于LLCL滤波的并联型APF的系统结构图，用二极管整流负载作为谐波源。图中usa、usb、usc为电网电压，L2a、L2b、L2c为LCL滤波器的网侧电感，L1a、L1b、L1c为APF侧滤波器电感，C2a、C2b、C2c为滤波电容，Lf为谐振电感，R1代表滤波电感L1的内阻和由每相桥臂上、下管互锁死区所引起的电压损失，R2代表滤波电感L2的内阻[10]。这里选择L1电感电流i1a、i1b、i1c，滤波电容C2、Lf两端电压Uca、Ucb、Ucc以及电网侧电感L2上的电流i2a、i2b、i2c为状态变量（式中uca,、ucb,、ucc,表示滤波电容C2两端电压）。在三相平衡且系统的开关很高时，根据现有理论可以使用状态空间平均法来解决此问题。使用开关函数在一个开关周期的平均值来代替开关函数本身，得出其对时间连续的状态空间平均模型，如式（1）所示

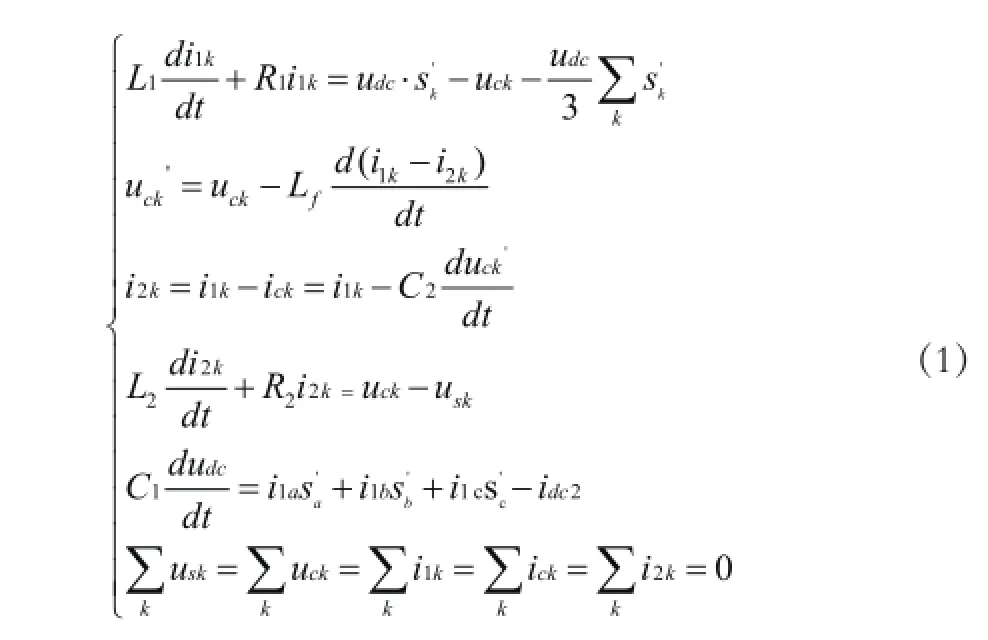
其中k=a，b，c

式中，Sk,为开关函数Sk的平均值，由于开关函数是一个幅值为1的脉冲，所以平均值Sk,等于其占空比。

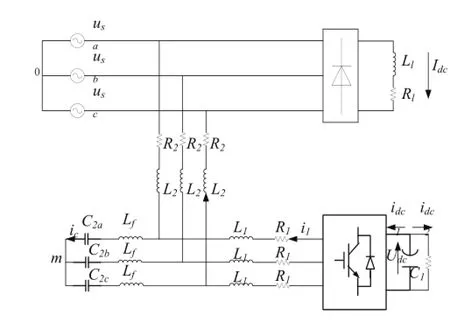
图1 基于LLCL滤波的并联型APF结构图

1. 2 LLCL滤波器的电路结构和传递函数

图2为LLCL滤波器拓扑，L1，L2，Cf分别为变换器侧电感、电网侧电感和滤波电容，Lf为LLCL型滤波器增加的串联在电容支路中的谐振电感，通过该电感与电容Rf对逆变器开关频率发生串联谐振，以最大化的衰减开关纹波，Cf为一个用于阻尼谐振的串联电阻。不考虑Rf作用时，LLCL型滤波器的传递函数为

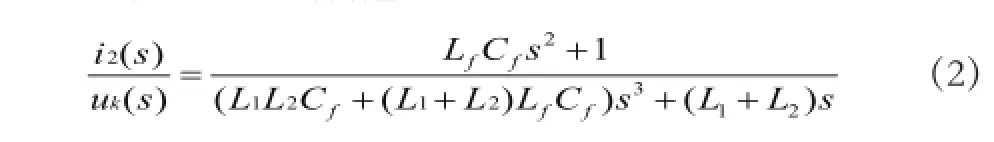
与普通的逆变器侧滤波器主要用来滤除各次谐波不同，针对APF，不但希望起到补偿作用的低次谐波分量可以不受影响地通过LLCL滤波器，而且希望获得一定的高频特性[15]。前者要求滤波器谐振频率尽量高，而后者却要

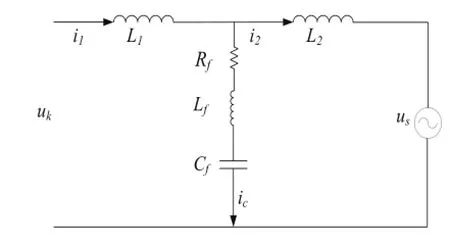
图2 LLCL输出滤波器拓扑

求谐振频率足够低。LLCL滤波器模型如图3所示。

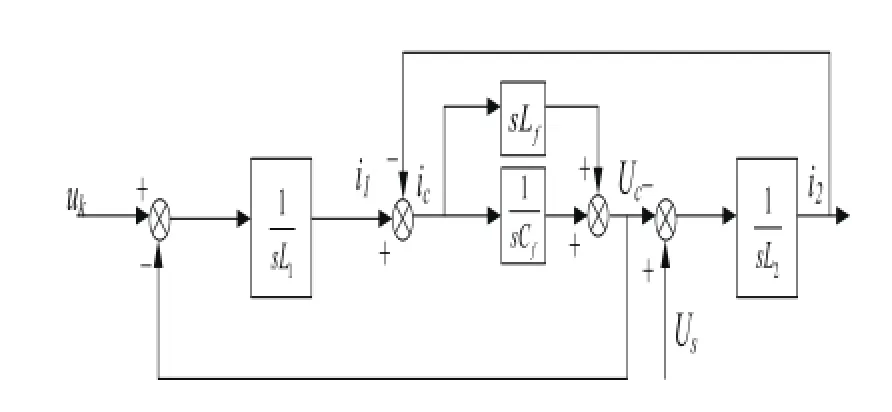
图3 LLCL滤波器模型

2 APF系统中产生延时的原因

目前，数字信号处理器（如DSP和FPGA）已经广泛应用于有源电力滤波系统当中。其有很多优点，如易于开发、易于更改控制算法、控制性能不易受环境的影响，没有元器件随时间老化以及参数漂移问题，然而也给有源滤波系统带来了延时问题。本文所研究的APF系统的数字化控制信号流程图如图4所示，图中的每个环节作为信号处理的一个过程都会给有源滤波系统带来或多或少的延时。

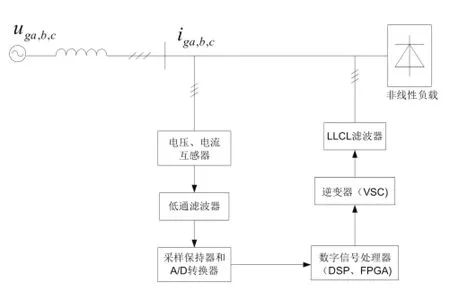
图4 APF数字化控制信号流程图

APF系统主要的延时环节具体分析如下：

1）电压、电流互感器会造成电压、电流波形的测量值滞后于一次侧实际电压、电流56～167μs；

2）A/D转换器通常集成采样保持器，不同性能的转换器造成的数据采样延时范围为10～102μs；

3）数字信号处理阶段引起的延时是指CPU完成数据计算任务所需要的时间，时间的长短主要与所选用的微处理器的运算速度以及程序指令的长短有关；

4）逆变器输出电路的延时，由于APF的逆变输出电路采用电力电子器件，电力电子器件的导通和关断都需要一定的时间，不同类型的开关器件开关时间相差比较大，可认为逆变器的开关时间为微秒级别；

5）在整个数字化控制APF系统中，由于控制的需要，各个微处理器之间需要通信，交换数据。控制指令一般每隔一定的周期才会更新一次,并不随被控对象的变化而变化，因此这是数字化控制所引入的另一种延时。

3 延时对补偿效果的影响

为了简化分析延时对APF补偿效果的影响，先作如下假设：

1）系统三相平衡，且只含有某一次的谐波，假设谐波次数为n，可以只对其中一相进行研究，谐波电流表示如下

由于电网内阻抗及APF交流侧LCL滤波器阻抗的存在，根据前文的分析，谐波电压源可以表示为

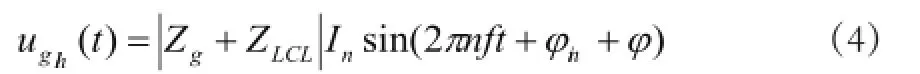
2）系统稳定运行，负载和电网没有发生动态变化。

3）APF的动态性能足够好，即不考虑延时时，逆变器交流侧输出电压能够完全跟踪谐波电压源，做到完全补偿。

根据上述假设，在没有延时的时候，APF输出的电压为

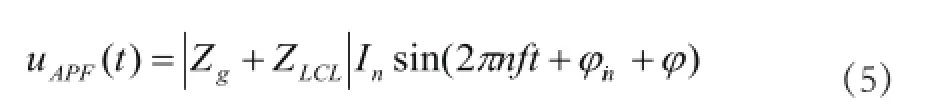
实际上由于延时的存在，APF交流侧输出的电压为

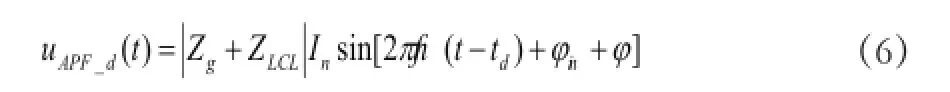
所以，跟踪误差可以表示为

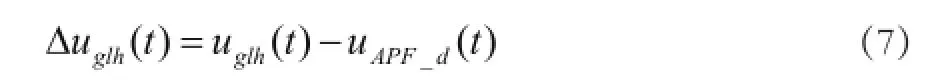
设 ϕd= 2 π n f td，则

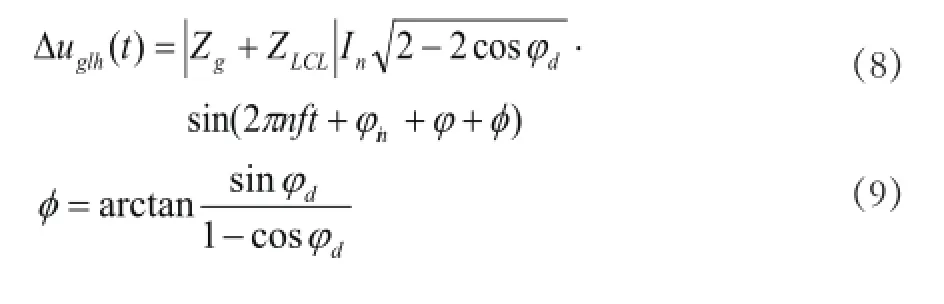
此时，电网侧残存的谐波电流为

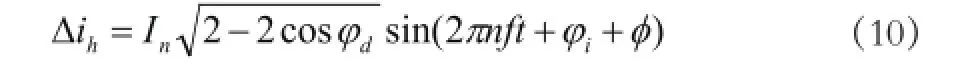
定义有源滤波器谐波补偿残余度为补偿之后和补偿之前的谐波幅值之比，因此

由式（12）和式（13）可知，残存的谐波电流的幅值与延时时间和谐波次数有关，图5为计算机仿真得到的第n次谐波的补偿残余度Dn与延时时间td之间的关系曲线。

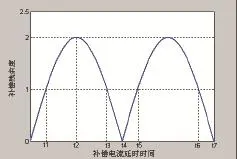
图5 n次谐波补偿残余度与延时时间之间的关系

由图5可知，当td＜t1时，APF对第n次谐波有补偿作用（虽然在t3～t5及t7～t9时间段，也有补偿作用，但是现实中的谐波电流不可能是单次的，在这些时间段内对其他次谐波可能就没有补偿作用，甚至严重放大，且考虑到APF的动态补偿特性，APF不应该工作在此两个及其之后的各延时时间段内）；而当td=t1时，APF恰好对第n次谐波不起作用；而当t1＜td＜t3时，APF不但不对电网中的第n次谐波进行补偿反而放大，产生了相当于无源LC滤波器的谐波电流放大现象。特别是当td=t2时，网侧中的n次谐波电流的幅值为负载电流中的n次谐波幅值的2倍，是谐波电流放大最严重的时候。综上分析可知：若想使APF对n次谐波有补偿作用，则必需满足td＜t1，即t1为APF对第n次谐波有补偿作用时的最大延迟时间，由式（12）可以求得APF对任意次谐波有补偿作用时对应的最大延时时间，即为对应谐波周期的六分之一。

图6为基波频率为50Hz的情况下，计算机仿真得到的最大延时时间td＿max与谐波次数n的关系曲线，可以看出：如果APF进行有效补偿的谐波次数越高，则输出的补偿电流的延时时间应越短

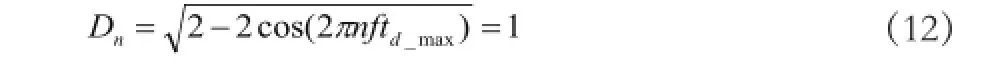
在实际的电网中一般都是多次谐波并存，可类似的分析延时对APF补偿效果的影响。如当系统中含有5、7、11、13次四种谐波，均方根值依次为I5、I7、I11、I13，则补偿后的谐波残余度为

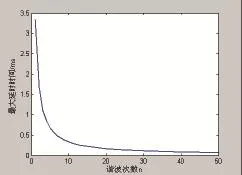
图6 最大延时时间与谐波次数之间的关系

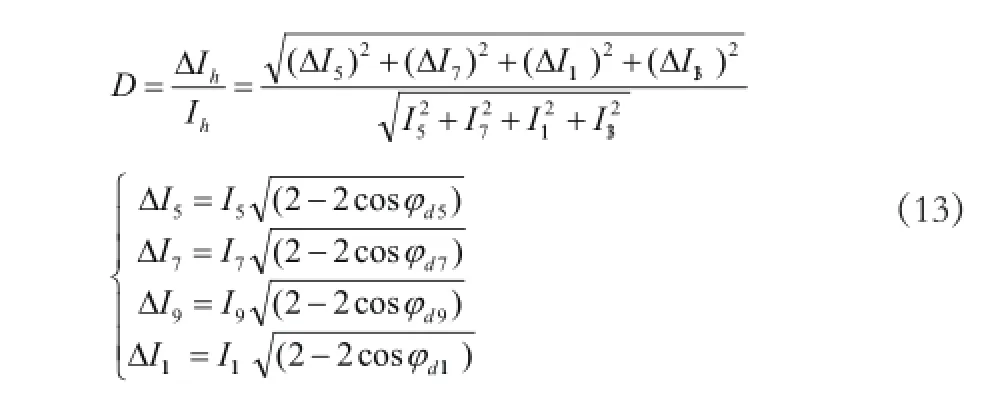
由式（13）可知，当电网中含有多次谐波时，随着延时的增大，谐波残余度也会增大。

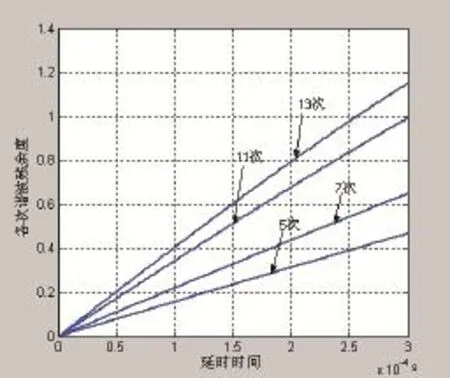
图7 各次谐波残余度与谐波次数及延时时间的关系曲线

图7为对应各次谐波的残余度与延时时间的关系曲线。由图可知，对同一次谐波，延时越大，谐波残余度也越大；对同样的延时时间，谐波次数越高，谐波残余度越大。在延时时间超过300μs时，APF对于11次谐波已经没有补偿作用，高于11次的甚至会被放大。

综上分析，APF的输出延时时间应越短越好。由于电力系统非线性负载种类繁多，电网中的高次谐波成分比较复杂，APF的最大允许延时时间也就很难确定。通常的做法是以网侧电流的畸变率THDig为依据，即只要补偿之后的畸变率小于补偿之前的就可以认为APF起到了谐波抑制作用。以畸变较严重的工频50Hz的方波为例，仿真结果表明：当延时时间为586μs时，APF已经不再有谐波抑制的作用，此时APF对高次谐波严重放大，低次谐波仍有些补偿作用，但是补偿前后的畸变率基本相同。因此，APF的最大延时时间应小于586μs。

4 加入补偿环节的重复学习控制

如图8所示，由重复控制理论可知，补偿器是根据被控对象 P(z)的特性而设置的，是重复控制器最关键的部分，直接决定着重复控制系统的性能。同一延时在被控对象不同频率上引起的相位滞后角度是不相同的，因此相位补偿意味着要针对扰动的每一个频率分量都需要给出合适的提前控制量。因此，补偿器 C(z)的相频特性最好就是被控对象P(z)相频特性的逆特性。如果被控对象P(z)的模型精确可知，那么取C(Z)=P-1(Z)，就可很方便地实现相位补偿。

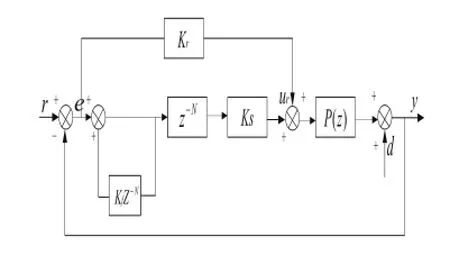
图8 重复学习控制框图

由前面的理论可知，系统前向通道设置了周期延时环节，这使得前向通道上的其他环节可以等效实现“分子阶次高于分母阶次”。因此，可以利用超前环节来实现相位补偿。由于已经假定了指令和扰动具有周期重复性，所以可以将控制量延时至下一个周期的适当时刻而获得超前性。例如为了等效实现k拍的相位超前，可以将控制量延迟(N-k)拍实施来等效实现。可见超前环节的模值恒为1，相角大小则与被控对象的频率成正比。因此，利用超前环节补偿相位，不会影响对幅值的补偿。

利用超前环节来实现相位补偿，仿照传统重复控制，补偿器C(Z)可表示成如下形式

可知重复学习控制器本身含有Ks重复控制增益项，此处补偿器中略去此比例项，仅由相位补偿和滤波器环节组成。滤波器S(Z)主要起以下作用：抵消被控对象较高的谐振峰，使之不会破坏系统的稳定性；增强前向通道的高频衰减特性，提高系统的稳定性和抗高频干扰能力。相对于基于模型对消方法的全频对消模式，这种补偿器只是致力于在中低频段实现对消，在高频段，系统本身就具有很强的衰减特性。

加入补偿环节后的重复学习控制框如图9所示。

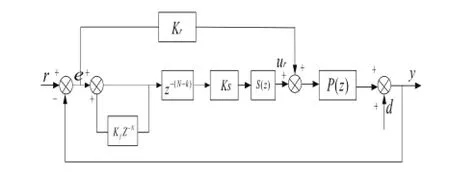
图9 加入补偿环节后系统的控制框图

是否能够将此方法运用到APF的重复学习控制器设计中，对系统的稳定性是否有影响，在此进行具体分析：

1）对于离散的控制系统而言，其本身就有带宽的限制。重复控制系统只是用来消除低于1/2采样频率的谐波信号。加入低通滤波器只会进一步降低系统的带宽，减少可滤除的谐波次数，对系统的稳定性没有影响。

2）一般APF主要用于补偿 25 次及以内的谐波，而且谐波主要集中在中低频段。从低通滤波器的幅频特性可知在控制器中引入低通滤波环节对系统的谐波抑制性能影响不大。

3）对于主电路变流器而言，考虑到开关管的开断以及死区效应，它本身就包含高阶成份。但是它们对系统的作用很小，引入低通滤波环节虽然会改变受控对象的特性，但对系统的稳定性几乎没有影响。

5 仿真与实验验证

5.1 Simulink仿真

考虑APF装置的延时环节，在电流的采样环节分别加入不同的延时，通过仿真，观察APF的实际补偿效果。

当延时Td=70μs时电压电流波形如图10所示。

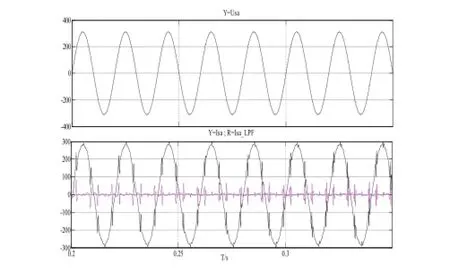
图10 延时70μs时系统A相电压电流波形

运用同一补偿器分别对以上三种延时进行补偿。图11～图13仿真的结果可以看出，延时的确对APF装置的实际补偿效果有较大的影响，相位补偿取超前3拍，滤波器取为2阶滤波器，补偿后A相电流电流THD都维持在3%左右，这说明了加入补偿环节是十分必要的。

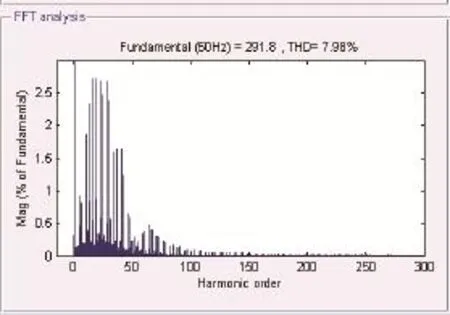
图11 系统A相电流THD

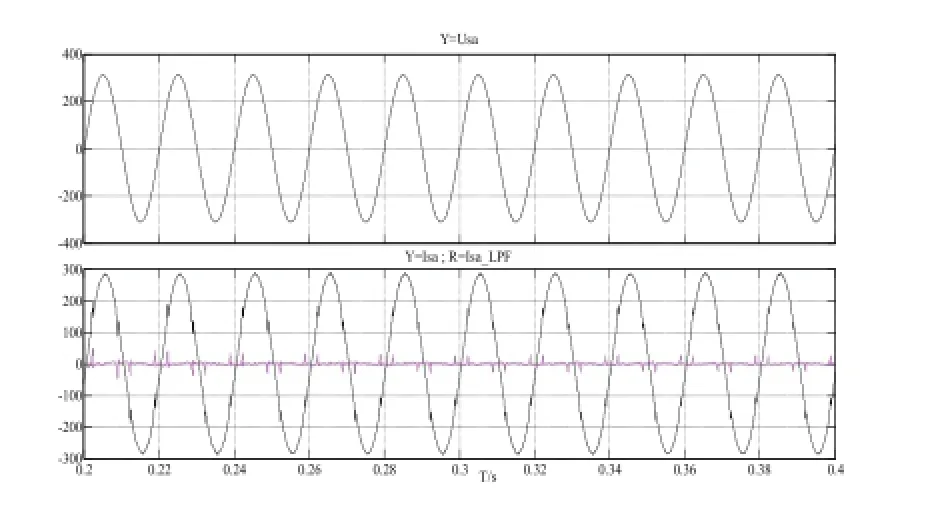
图12 加入补偿环节后A相电压电流波形

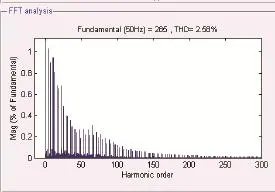
图13 加入补偿环节后A相电流THD分析

5.2 实验验证

加入补偿环节的APF动态性能试验，设定APF恒无功控制方式，APF设定10%额定容量突增至90%额定容量运行，再由90%额定容量突减至10%额定容量运行，装置输出达到目标值的90%所用的时间。用电能质量分析仪测定APF突升与突降时间。

图14和图15可以看出来在APF容量突增和突减时，APF的无功指令的动态响应很快，在电能质量分析仪中得出无功跟踪响应时间小于等于10ms。

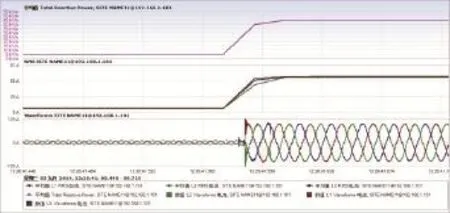
图14 APF无功指令响应时间（突增）波形

图15 APF无功指令响应时间（突减）波形

图16和图17可以看出来在APF容量突增和突减时，APF的谐波补偿的动态响应很快，在电能质量分析仪中得出谐波响应时间小于等于10ms。

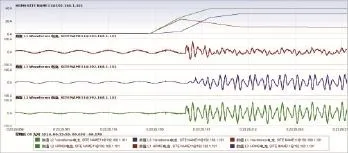
图16 谐波响应时间（突增）测量波形

综上所述，加入补偿环节的重复学习控制，一定的延时下APF的无功指令和谐波补偿的动态响应很迅速。

6 结束语

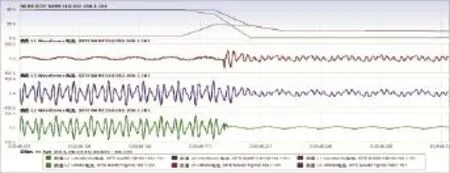
图17 谐波响应时间（突减）测量波形

针对实际的有源滤波装置延时环节的存在，对延时的产生以及对最终补偿效果的影响都进行了理论分析，得出了谐波残余度与延时时间的具体关系。提出了利用补偿环节C(Z)来补偿延时以及提高APF对高频分量的衰减，改善滤波效果。仿真和实验证明了这种方法的有效性，在一定的延时下仍然可以取得较好的补偿效果。

[1]IEEE Std. 519-1992． IEEE recommended practices and requirements for harmonic control in electric power systems[In].1993.

[2] GB/T 14549-93 电能质量公用电网谐波[S]. 北京：中国标准出版社，1994.

[3] 闫光太，梁甲文，王新涛，等. 利用暂态幅值故障测度的谐振电网故障选线[J]. 电力系统保护与控制，2015，43(8):65-67.

[4] 邹志翔，王政，等．双模结构重复控制器在单相并联有源滤波器中的应用[J]. 中国电机工程学报，2013,33(36)： 88-93．

[5]周柯，王凯，等．一种改进型并联混合有源滤波器及其控制[J]. 中国电机工程学报， 2012,32(30)： 67-71．[6] 张霞，陈允平．并联有源电力滤波器的自学习控制[J].电力系统自动化， 2003,23(7)： 58-62．

[7] 查晓明，陈允平．无源与有源结合电力滤波器阻尼谐波器阻尼谐波振荡的重复学习Boost变化控制[J]．电工技术学报， 2004, 19(6)： 30-35．

[8] 查晓明，孙建军，陈允平．并联型有源电力滤波器的重复学习Boost变化控制策略[J]. 电工技术学报，2005， 20(2)： 56-62．

[9] 武健，徐殿国，何娜．并联有源滤波器输出LCL滤波器研究[J]. 电力自动化设备，2007,27(2)： 17-20．

[10]张月明，李俊，刘嘉，等. PI电流内环控制器实现的链式APF在外超导磁体中的应用[J]. 电力系统保护与控制，2015,43(1)：123-127.

2016-11-26）