直驱永磁同步风电机组的无功功率支撑策略

杨骏华，陈永强，刘扬

（西华大学电气与电子信息学院，四川 成都 610039）

直驱永磁同步风电机组的无功功率支撑策略

杨骏华，陈永强，刘扬

（西华大学电气与电子信息学院，四川 成都 610039）

电网准则要求风力发电机组应该具有并网点电压调节能力。基于这一问题，提出了直驱永磁同步风力发电系统无功功率支撑策略。建立了风力涡轮机、永磁同步电机以及电压源型变换器的数学模型，分析了网侧和机侧变换器的控制原理，给出了系统控制框图。通过Matlab/Simulink仿真软件建立了1.5 MW直驱永磁同步风力发电系统的仿真模型，分别对电网正常和电网故障情况进行了仿真研究。实验结果表明所提出的无功功率支撑策略在直流母线电压稳定的基础上能够提升公共耦合点（point of common coupling，PCC）电压。当风电场中多台风电机组采用该方法时，能够帮助PCC电压恢复至正常范围。

直驱永磁同步风力发电系统；无功支撑；最大功率跟踪控制；并网变换器；矢量控制

能源短缺和全球变暖问题已经引起了世界各国的广泛关注，快速发展可再生能源并网发电技术有利于缓解这一问题。在多种可再生能源中，风力发电发展最快，尤其在欧洲国家，如丹麦风力发电的比例已经达到30%，2010年底全球装机容量约为200 GW［1］。为了完成减排目标，我国也相继出台多种政策和机制鼓励风力发电系统发展，在2010年，总的装机容量已经达到44.73 GW［2］。

目前应用最为普遍的2种结构分别为双馈风力发电系统和直驱永磁同步风力发电系统［3］。与双馈风力发电系统相比，永磁同步风力发电机具有的优势主要包括：无需变速齿轮箱，减小了维修成本；定子侧与电网通过背靠背变换器相连，当电网发生短路故障期间，对机侧变换器的运行影响较小，容易实现故障穿越控制［4-6］。

随着风力发电机组装机容量不断增加，电网准则要求风力发电系统应具有并网点电压调整能力，在大型风电场传输系统中，线路阻抗通常为感性，因此可以采用向电网注入无功功率的方式对PCC电压进行支撑。

针对这一问题，文献［7］对风电场低电压穿越无功支撑进行了仿真研究，主要采用静止同步补偿器（static synchronous compensator，SΤAΤCOM）和静止无功补偿器（static var compensator，SVC）作为无功补偿装置，并且比较了两者的优势。文献［8］提出了风电场无功电压协调控制策略，根据PCC电压和功率因数进行分区，分别考虑了不同情况，该方法通过调度指令进行下发，而调度指令下发时间周期较长，而故障时间较短难以实现快速无功支撑。文献［9］研究了通过加设储能装置来控制直流母线电压，而网侧变换器实现无功支撑控制策略。

从传统无功功率支撑控制方案可以看出，在PCC电压发生跌落时，通常采用静态无功补偿装置或者储能系统来保证风电机组向电网提供无功支撑。尽管该方法能够实现动态无功支撑，但是加设的大容量无功补偿装置和储能系统将会增加系统成本和控制的复杂性。

针对这一问题，本文提出了一种新型无功功率支撑控制策略，建立风力涡轮机、全功率变换器以及永磁同步电机的数学模型，给出了网侧变换器和机侧变换器的控制策略，并且进行了详细分析。

为了验证本文所提出控制策略的可行性和有效性，通过Matlab/Simulink仿真软件搭建了额定功率为1.5 MW的风力发电系统并网模型，对电网正常和故障情况进行了仿真研究。

1 风力发电系统的数学建模

直驱永磁同步风力发电系统主要由风力涡轮机、永磁同步电机和全功率变换器组成，下面分别建立各个组成部分的数学模型。

1.1 风力涡轮机数学模型

风力机从风能吸收的功率可以表示为［10］

式中：ρ,R,V,β,λ分别为空气密度、桨叶半径、风速、桨距角和叶尖速比；Cp(λ,β)为风能利用系数。

风能利用系数Cp的大小与叶尖速比和浆距角有关。反映了风能转化为发电量的效率。Cp(λ,β)可以表示为

1.2 功率变换器的数学模型

直驱永磁同步风力发电系统的网侧变换器的系统结构框图如图1所示，主电路采用电压源型两电平变换器，网侧接有电感滤波器，直流侧接有直流电容，直流电容的接入能够使风力发电系统的网侧变换器和机侧变换器实现解耦，进而保证网侧变换器和机侧变换器独立运行。

图1 网侧变换器的结构框图Fig.1 The structure diagram of grid-side converter

当以d轴电压进行定向时，网侧变换器在两相同步旋转坐标系下的数学模型为［11］

式中：ed,eq分别为PCC电压的dq轴分量；sd,sq分别为开关函数的dq轴分量；id,iq分别为逆变器输出电流的dq轴分量；ω为基波角频率；Lg为滤波电感；R为滤波电感等效串联电阻；C为直流母线电容；udc为直流电压；idc为直流电流。

1.3 永磁同步电机的数学模型

将同步坐标系的d轴定向于转子磁极，而q轴超前于d轴90°，在dq坐标系下能够得到永磁同步电机的定子电压方程和电磁转矩方程为

式中：usd,usq分别为定子电压的dq轴分量；isd,isq分别为定子电流的dq轴分量；Rs为定子电阻；ωe为转子电角速度；Ld,Lq为定子dq轴自感；Ψf为转子永磁铁磁链；Te为电磁转矩；p为极对数。

2 风力发电系统的控制策略

根据电网准则要求，风力发电系统在电网发生短路故障时应具有动态无功支撑能力。为了实现这一控制目标，本文提出了一种具有无功功率支撑能力的控制策略。下面分别对网侧和机侧变换器的控制策略进行分析。

2.1 网侧变换器的控制策略

假设变换器额定容量为S，逆变器输出有功功率为P，无功功率为Q，根据三者之间的关系能够得到：

当有功功率一定时，根据式（6）能得到最大输出无功功率为

为了实现无功功率支撑，设置无功功率最大值为无功功率参考值，当以d轴电网电压进行定向时，逆变器输出有功和无功功率可以表示为

根据式（9）可以算出电网故障期间无功电流参考值为

网侧变换器的控制策略既要保证直流电压恒定，又要实现动态无功支撑，其控制结构如图2所示。电压外环控制直流母线电压，其误差信号经过PI调节器得到d轴电流参考值，而q轴电流参考值与电网电压状况有关，当电网电压大于0.9（标幺值）时，电网电压正常，此时q轴电流参考值为0，运行在单位功率因数模式；当电网电压小于0.9（标幺值）时，电网电压发生跌落，此时q轴电流参考值可以根据式（10）进行计算得到，工作在无功功率支撑模式，可控开关动作可以根据电网电压幅值情况进行控制。为了消除dq轴之间的耦合和PCC电压对系统的影响，采用解耦和前馈控制，通过合成最终得到三相调制信号，将其送入SPWM调制模块得到驱动信号。

图2 网侧变换器的控制策略Fig.2 The control strategy of grid-side converter

2.2 机侧变换器的控制策略

机侧变换器的主要控制目标是实现最大功率跟踪控制，为了说明最大功率跟踪原理，根据表1能够得到风力涡轮机特性曲线。

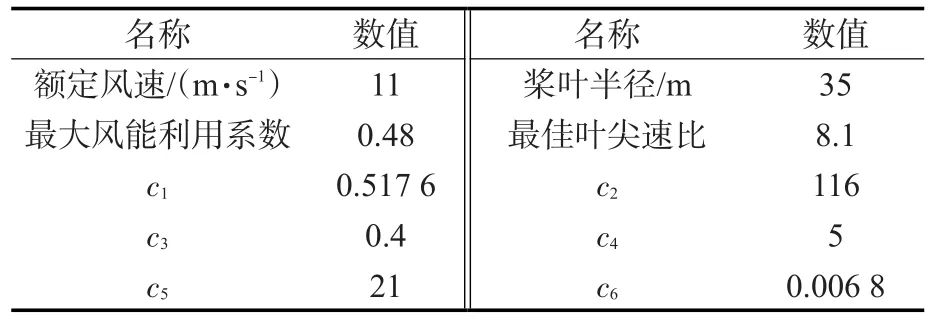
表1 风力涡轮机的主要参数Tab.1 The main parameters of wind turbine

从图3可以看出，系统的输出功率与风力涡轮机的转矩随着风速的逐渐增加而相应增加，反之亦减小。在风速一定的情况下，存在唯一的最佳转速对应着最大功率点，因此可根据最大功率跟踪算法获得最佳转速，再通过转速的闭环控制，实现最大功率跟踪运行［12］。

图3 风力涡轮机特性曲线Fig.3 The characteristic curves of wind turbine

机侧变换器的控制结构如图4所示，主要采用转速外环和电流内环控制策略。首先通过最大功率跟踪控制策略得到转速外环参考值，将其与实际转速相减经过PI调节器得到转矩电流指令，设置励磁电流为0。将电流指令值与实际值相减经过PI调节器得到调制信号，根据式（4）同样可以看出机侧变换器的dq轴之间也是存在耦合的，因此为了消除耦合加入了解耦环节，最终将调制信号通过SPWM模块生成IGBΤ驱动信号。

图4 机侧变换器的控制策略Fig.4 The control strategy of machine-side converter

3 仿真研究

为了验证本文研究控制算法的有效性，通过Matlab/Simulink仿真软件搭建了直驱永磁同步风力发电系统仿真模型，系统结构如图5所示。电网线电压有效值为35 kV，主网与风电机组通过690 V/35 kV变压器连接，PCC线电压有效值为690 V，升压变与主网之间的线路距离为37 km，变换器的额定容量为1.5 MV·A，网侧滤波电感为5 mH，直流母线电容为10 mF，直流母线电压为1 200 V，风力涡轮机参数如表1所示，永磁同步电机定子电压有效值为690 V，极对数为32，额定磁链为5.7 Wb。

图5 直驱永磁同步风力发电系统结构Fig.5 The system structure of direct drive PMSG

3.1 电网正常情况

首先对电网正常情况下进行仿真研究，仿真结果如图6所示。

图6给出了电网电压正常情况下的仿真结果。在初始条件下风速为9 m/s，通过网侧和机侧变换器的控制能够实现最大功率跟踪，并且保证直流电压为1 200 V。在1 s和2 s时，风速分别由9 m/s突变到11 m/s，11 m/s突变到10 m/s，从图中可以看出，在风速突然增加或者突然减小时，采用本文研究的控制方法能够根据风速的变化实现最大功率点运行，于此同时能够保证直流电压稳定，逆变器的并网电流总谐波畸变率小于5%，满足IEEE std 519规定的并网要求，仿真结果验证了所提控制算法的可行性和有效性。

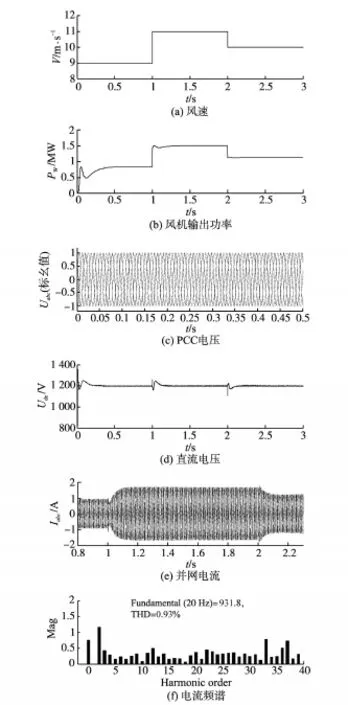
图6 电网正常情况的仿真结果Fig.6 The simulation results of normal grid condition

3.2 所提控制算法的电网电压跌落

前面对电网正常情况下的风力发电系统最大功率跟踪控制算法进行了可行性验证。下面考虑电网附近处三相短路，此时仿真结果如图7所示。

图7给出了电网短路故障情况下的仿真结果，初始条件与图6一致。从图7a中可以看出，采用本文提出的控制策略向电网注入无功功率能够帮助PCC电压抬升，且逆变器输出有功功率不变，维持有功功率平衡，保持直流母线电压恒定。在2 s时电网故障清除，网侧变换器恢复至单位功率因数运行模式，此时无功功率为0。

图7 电网短路故障情况的仿真结果Fig.7 The simulation results of grid short circuit fault condition

本文提出的控制策略能够进一步拓展到风电场，在风电场中一个节点将会接入多个风电机组，此时输出无功功率能力更强，输出无功功率越大PCC电压抬升越高，如表2所示。可以看出，采用本文提出的方法，当同时接入6台风电机组时可以保证PCC电压幅值达到0.9（标幺值）以上，使其处于正常范围内。

表2 多台风电机组接入情况的PCC电压幅值Tab.2 PCC voltage amplitude of multiple wind turbines

4 结论

针对风力发电系统的动态无功支撑问题，本文提出了一种新型无功功率支撑控制策略，与以往的无功支撑方案相比，在没有配置储能系统的情况下，在电网故障期间本文提出的策略仍然能够保证直流母线电压稳定，并且实现风力发电系统最大功率跟踪运行，同时最大限度实现无功功率支撑，抬升PCC电压。当节点中接入多个风电机组时，能够使得PCC电压恢复至0.9（标幺值）以上，使其处于正常范围内。采用本文的控制策略能够减小储能装置和无功补偿装置配置容量，降低了系统投资成本以及控制的复杂性，具有一定的工程应用价值。

［1］Blaabjerg F，Ma K.Future on Power Electronics for Wind Turbine Systems［J］.IEEE Journal of Emerging and Selected Topics in Power Electronics，2013，1（3）：139-152.

［2］Jiang Liping，Chi Yongning，Qin Haiyan，et al.Wind Energy in China［J］.IEEE Power and Energy Magazine，2011，9（6）：36-46．

［3］Marco Liserre，Roberto Cárdenas，Marta Molinas，et al.Over⁃view of Multi-MW Wind Turbines and Wind Parks［J］.IEEE Transaction on IndustrialElectronics，2011，58（4）：1801-1095.

［4］宋卓彦，王锡凡，滕予非，等.变速恒频风力发电机组控制技术综述［J］.电力系统自动化，2010，34（10）：8-17.

［5］王凤翔．永磁电机在风力发电系统中的应用及其发展趋向［J］.电工技术学报，2012，27（3）：12-24.

［6］夏长亮.永磁风力发电系统及其功率变换技术［J］.电工技术学报，2012，27（11）：1-13.

［7］刘云，刘亚丽，胡晓辉，等.基于PSCAD的风电场低电压穿越无功支撑仿真研究［J］.智能电网，2014，2（2）：46-51.

［8］陈宁，何维国，钱敏慧，等.风电场无功电压控制系统设计和应用［J］.电力系统自动化，2011，35（23）：32-36．

［9］Saad Sayeef，Nishad Mendis，Kashem Muttaqi，et al.Enhanced Reactive Power Support of a PMSG Based Wind Turbine for a Remote Area Power System［C］//Australasian Universities Power Engineering Conference，Christchurc，2010：1-5.

［10］Li Shuhui，Timothy A Haskew，Richard P Swatloski，et al.Op⁃timal and Direct-current Vector Control of Direct-driven PMSG Wind Turbines［J］.IEEE Transaction on Power Elec⁃tronics，2012，58（4）：1801-1095.

［11］马宏伟，李永东，郑泽东，等.电流环模型预测控制在PWM整流器中的应用［J］.电工技术学报，2014，29（8）：136-141.

［12］赵仁德，王永军，张加胜.直驱式永磁同步风力发电系统最大功率追踪控制［J］.中国电机工程学报，2009，29（27）：106-111.

Reactive Power Support Strategy for Direct Drive Permanent Magnet Synchronous Wind Turbine

YANG Junhua，CHEN Yongqiang，LIU Yang
（School of Electrical and Information Engineering，Xihua University，Chengdu 610039，Sichuan，China）

Grid criterion requires that the wind power generating system should have PCC voltage regulation ability.Based on this problem，the reactive power support strategy was proposed for direct drive permanent magnet synchronous wind power generation system.The mathematical model of wind turbine，permanent magnet synchronous motor and voltage source converter was established，the control principles of the grid side and the machine side converter were analyzed，and the control graphs were also given.The simulation model of 1.5 MW direct drive permanent magnet synchronous wind power generation system was established by Matlab/Simulink simulation software.Simulation results show that the proposed control strategy can improve the point of common coupling（PCC）voltage on the basis of DC bus voltage stability.When the proposed control strategy is applied for multiple wind turbine generators in the wind farm，it can restore the PCC voltage to the normal range.

direct drive permanent magnet synchronous wind power generation system；reactive support；maximum power tracking control；grid-connected converter；vector control

TM614

A

10.19457/j.1001-2095.20170209

2016-01-15

修改稿日期：2016-07-08

杨骏华（1990-），男，硕士，Email：460235560@qq.com