高频方波注入的永磁电机无传感器控制改进算法

薛映霞，陈庆，何凤有

（中国矿业大学信息与电气工程学院，江苏 徐州 221008）

高频方波注入的永磁电机无传感器控制改进算法

薛映霞，陈庆，何凤有

（中国矿业大学信息与电气工程学院，江苏 徐州 221008）

为提高高频信号注入的内置式永磁同步电机无传感器控制系统的带宽，提出了一种方波信号注入的无传感器控制改进算法。利用方波信号代替传统的正弦波信号，将注入电压频率提高至逆变器的开关频率，通过简单的算术运算求取高频载波电流和基频电流，避免了带通滤波器和低通滤波器的使用，简化了信号处理过程，提高了系统的动态响应速度。仿真和实验结果验证了改进算法的可行性和有效性。

永磁电机；高频方波注入；无传感器控制；带宽；算术运算

永磁同步电动机因其功率密度高、功率因数高、动态响应快等优点已广泛应用于交流传动领域与伺服控制系统中［1］。在高性能的永磁同步电机矢量控制调速系统中，转子磁极位置信息通常由机械式传感器获得。由于其成本高、可靠性低、在特殊场合实现困难等局限性，学者们提出了无传感器控制技术。即通过检测电机的电流（电压）信号，经过一定的信号处理与调制，估算出转子的位置信息［2-3］。

永磁同步电动机无传感器控制技术按其适用速度范围通常分为两类：一类是电机运行在中、高速工况下的无传感器控制技术；另一类是适用于零、低速运行的无传感器技术［4］。前者是基于电动机的反电动势信息获取转子磁极位置，在中、高速范围内有较好的运行特性。由于反电动势与转速成正比关系，低速甚至零速时，反电动势较小，信噪比较低，估算精度会严重下降。后者是利用电机的凸极特性，采用高频信号注入的方法提取位置信号，该方法完全不受电机速度的影响，在零低速范围内估算误差较小。但高频注入会带来额外的转矩脉动，使电机产生振动、噪声。同时，高频信号注入法的信号处理过程非常复杂，滤波器的使用会严重限制控制系统的带宽，且定子电流幅值的增大会降低角度跟踪的准确性［5-6］。因此，适于零、低速运行的高频注入法与中、高速工况下的反电动势法的复合控制法成为全速域无传感器控制的发展趋势。

为了降低信号处理的复杂性，提高控制系统带宽，Seung-kiSul教授提出了方波信号注入的无传感器控制技术。文献［6］中注入方波信号代替传统的正弦波信号，且增大注入信号频率至PWM开关频率一半，可省去用于降低噪声的低通滤波器，一定程度上提高了响应速度。但是，仍然需要用于获取基波电流的低通滤波器以及高频电流的带通滤波器，由这些滤波器带来的信号时延仍然会限制无传感器控制系统的带宽。文献［7］中将注入方波电压频率增大至PWM开关频率，在1个信号注入周期内做3次算术运算得出高频载波电流信号，避免使用带通滤波器，但仍需低通滤波器获取反馈电流信号。文献［8］在1个开关周期内测量4次电流，减小了负载扰动、转速给定变化等动态过程中转子位置的观测误差，但对处理器的运算能力提出了更高的要求。

本文提出了一种基于高频方波注入的无传感器控制改进算法，在1个信号注入周期内，测量2次电流，通过简单的算术计算可获取基波电流以及高频响应电流，不需要任何滤波器。因此信号处理过程中由带通滤波器和低通滤波器产生的时延也将消失。改进的无传感器技术的实现方法将会提高系统的动态响应速度。

1 高频方波注入的无传感器控制原理

图1是典型的高频信号注入的无传感控制的原理框图，主要包括3部分：第1部分为高频信号注入部分，通过注入特殊的连续的高频信号获取电机的凸极信息。第2部分是信号处理部分，从定子电流中分解出注入电压感应的高频载波电流，通过信号处理提取出与转子位置相关的信号（位置误差信号）。第3部分通过位置观测器估算出磁极位置与转速信息［9］。

图1 无传感器控制基本原理框图Fig.1 Basic principle diagram of sensorless control

理论上讲，高频信号可以注入任意的坐标系。当注入到同步坐标系下估算的d轴时（也称脉振信号注入）信号处理过程较简单，且估算性能较好。注入高频方波电压信号为

式中：^为估计的同步旋转坐标系；Uh为注入电压的幅值。

常用的从高频载波电流信号中提取位置信号的方法有两种：一种是分别提取两相静止坐标系下的高频电流iαh,iβh,并利用反正切函数得到转子位置角。文献［6］为了降低计算过程中的噪声信号，避免每半周期正弦信号值为零导致反正切函数无解的情况，注入的高频信号采用方波信号代替正弦波信号。但为了获取基波电流以及高频载波电流，系统中仍需带通滤波器和低通滤波器。其原理图如图2所示。

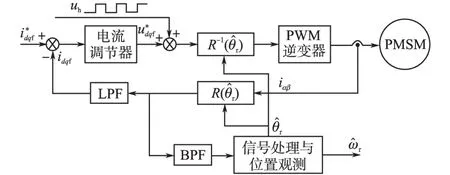
图2 方波注入的无传感器控制原理框图Fig.2 Sensorless control diagram based on square wave signal injection

图3 利用电流变化率获取位置信息Fig.3 Obtained rotor position information through current change rate

2 提出的信号处理方法

2.1 电流提取方法

将高频方波电压信号注入估计的同步旋转坐标系，忽略高次谐波电流，定子电流包含的成分主要有方波电压激励作用产生的载波电流用于电流反馈的基波电流,即

注入的高频方波电压波形以及产生的载波电流响应波形如图4所示。注入电压的频率与逆变器的开关频率相等，且在1个PWM周期内测量2次电流。

图4 方波电压注入下估算同步坐标系下的高频响应电流Fig.4 High-frequency current based on square injection in estimated synchronous-frame

考虑到1个开关周期内基波电流基本不变，因此有：

所以对连续的2个电流采样值做算术运算即可得到基波电流。可以省去为获取基波电流采用的低通滤波器，由此引起的信号延迟以及幅值衰减也可避免。

2.2 估算的同步坐标系下的信号处理方法

在高频低速的情况下，忽略定子电阻以及旋转电动势的影响，可得在同步旋转d-q坐标系下，永磁同步电机的简化模型：

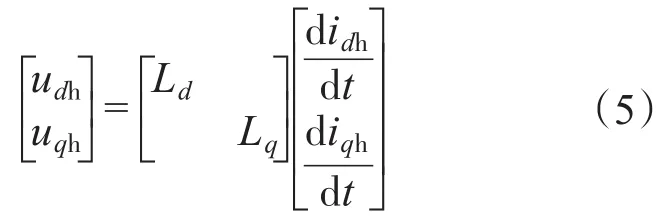
式中：Δθ为估算d轴和实际d轴的夹角，即位置估算误差角。

根据式（5）、式（6）得：

因此，可测量的估算坐标系下的电流信号为

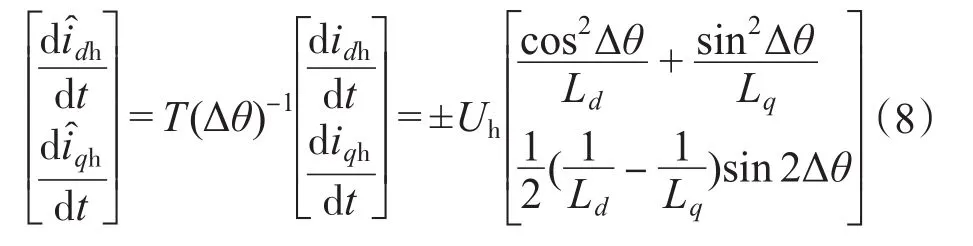
由图4可知，在方波信号的正（负）半周期内，高频感应电流的幅值不变，且注入电压的频率较高，因此可以采用式（8）的离散形式得到电流的变化率，即

式中：ΔT为电流的采样周期。

由式（9）可得，当位置误差Δθ为零时，高频方波电压仅仅在轴上感应出高频载波电流。因此可以利用轴高频电流获取转子位置误差信息，仅需控制轴高频电流为零即可实现转子位置的无误差跟踪。当误差角Δθ很小时，有sin2Δθ≈2Δθ，此时，误差角与成正比关系：

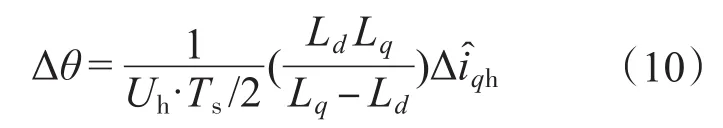
考虑到注入电压的极性，则有：

利用传统的锁相环技术或含转矩前馈控制的位置观测器校正式（10）中的误差信号即可获取转子的位置信息。本文提出的信号处理方法可省略带通滤波器以及低通滤波器，通过简单的算术运算即可获得高频电流和反馈电流信号。由此可避免信号处理过程中电流信号以及位置信号的延迟，同时将注入的方波信号频率提高至逆变器的开关频率，很大程度上提高了无传感器控制系统的带宽。基于改进算法的永磁同步电机无传感器矢量控制系统框图如图5所示。

图5 基于改进算法的无传感器控制系统框图Fig.5 Diagram of sensorless control based on improved algorithm

3 仿真验证

为验证改进算法的可行性，在仿真软件Matlab/Simulink中搭建基于方波注入的无传感器控制系统仿真模型。IPMSM模型参数为：Ld=12 mH,Lq=20 mH,Rs=0.636 Ω,转动惯量0.01 kg·m2，极对数4，永磁体磁链1.19 Wb。注入方波电压的幅值为50 V，频率为5 kHz，逆变器开关频率为5 kHz，电流采样频率为10 kHz。从负载阶跃和转速阶跃2个动态过程验证所提算法的正确性，为验证系统的动态响应，分别测试了转速环和电流环的带宽。

图6为转速阶跃时，采用改进算法得出的转速和位置估算仿真波形。电机空载运行，给定转速为100 r/min，并于0.55 s时给定转速由100 r/min跳变到50 r/min。

图6 转速阶跃仿真结果Fig.6 Simulation result when speed step

由图6可以看出，估算转速和位置都能较好地跟踪电机的给定速度和实际位置，稳态时转子位置估算误差角约为8°（电角度）。当系统采用文献［7］所示的信号处理方法作无传感器运行时，稳态位置误差角约为15°（电角度）。图7为负载阶跃时的仿真结果，分别为估算转速、电磁转矩以及估算位置波形。电机空载启动，给定转速100 r/min，0.4 s时加载4 N·m，0.7 s时电机又作空载运行。根据速度曲线，加减负载时转速的波动较小，可得系统有一定的抗负载扰动性能。

图7 负载阶跃仿真结果Fig.7 Simulation result when load step

为进一步验证系统的瞬态响应速度，分别测试了转速环和电流环的带宽。测试结果如图8、图9所示。

图8 转速环带宽测试Fig.8 Bandwidth measurement of speed loop

图9 电流环带宽测试Fig.9 Bandwidth measurement of current loop

图8a为给定速度频率5 Hz，幅值为100 r/min的正弦波，可以看出估算速度有较好的跟踪性能。当给定频率上升至30 Hz时，从图8b中可以看出估算速度与给定转速的相位相比，有大约50°的滞后，可得速度环的带宽约为30 Hz。当无传感器控制系统采用图3所示的信号处理方法作无传感器运行时，速度环带宽为25 Hz［7］。从图9b可以看出，由于取消了低通滤波器，电流环的带宽可达到300 Hz以上。

4 实验验证

对图5所示的无传感器矢量控制系统进行实验验证。实验电机采用22 kW的内置式永磁电机，电机参数为：定子电阻0.16Ω，极对数3，直轴电感10 mH，交轴电感30 mH，永磁体磁链1.2 Wb，采用30 kW的直流电机作为负载与永磁电机对拖。控制算法均由ΤMS320F2812 DSP实现。图10为电机空载运行时，给定速度变化时的估算速度以及位置波形。可以看出估算转子位置可以很好地跟踪实际位置，电机在无传感器方式下可以稳定运行。实验中由于信号采样以及系统运算等因素，稳态时估算误差约为12°（电角度）。图11为负载阶跃变化时的实验波形。电机空载稳定运行后，加额定负载，从转速曲线可以看出系统有一定的抗扰特性。

图10 转速阶跃实验波形Fig.10 Experimental waveform when speed step

图11 负载阶跃仿真波形Fig.11 Experimental waveforms when load step

5 结论

基于高频信号注入的永磁同步电机无传感器控制系统，本文采用方波信号代替传统的正弦波信号注入，采用简单的算术运算即可获取高频感应电流和基波电流，避免了带通滤波器和低通滤波器的使用，并且简化了无传感器控制算法。仿真和实验结果表明估算速度、位置都能有效地跟踪实际转速与转子位置，并且将估算位置角和估算速度用于闭环系统时，无传感器控制系统有较好的动态响应速度与抗负载扰动性能。通过采用提出的改进算法，逆变器开关频率为5 kHz时，转速环的带宽可达到30 Hz，接近于有传感器控制系统的带宽［6］。

［1］李永东，朱昊.永磁同步电机无速度传感器控制综述［J］.电气传动，2009，39（9）：3-10.

［2］Kulkarni A B，Ehsani M.A Novel Position Sensor Elimination Technique for the Interior Permanent-magnet Synchronous Mo⁃tor Drive［J］.Industry Applications，IEEE Transactions on，1992，28（1）：144-150.

［3］Raca D，García P，Reigosa D D，et al.Carrier-signal Selection for Sensorless Control of PM Synchronous Machines at Zero and Very Low Speeds［J］.Industry Applications，IEEE Trans⁃actions on，2010，46（1）：167-178.

［4］谷善茂，何凤有，谭国俊，等.永磁同步电动机无传感器控制技术现状与发展［J］.电工技术学报，2009，24（11）：14-20.

［5］Chen J L，Liu T H，Chen C L.Design and Implementation of a Novel High-performance Sensorless Control System for Interi⁃or Permanent Magnet Synchronous Motors［J］.Electric Power Applications，IET，2010，4（4）：226-240.

［6］Yoon Y D，Sul S K，Morimoto S，et al.High-band Width Sensor⁃less Algorithm for AC Machines Based on Square-wave-type Voltage Injection［J］.Industry Applications，IEEE Transac⁃tions on，2011，47（3）：1361-1370.

［7］Kim S，Ha J I，Sul S K.PWM Switching Frequency Signal In⁃jection Sensorless Method in IPMSM［J］.Industry Applica⁃tions，IEEE Transactions on，2012，48（5）：1576-1587.

［8］王莉娜，郝强.基于高频方波信号注入的PMSM无传感器低速运行研究［J］.电气传动，2015，45（6）：20-25.

［9］Park N C，Kim S H.Simple Sensorless Algorithm for Interior Permanent Magnet Synchronous Motors Based on High-fre⁃quency Voltage Injection Method［J］.Electric Power Applica⁃tions，IET，2014，8（2）：68-75.

Improved Algorithm of Sensorless Control of PMSM Based on High Frequency Square Wave Signal Injection

XUE Yingxia，CHEN Qing，HE Fengyou
（School of Information and Electrical Engineering，China University of Mining&Technology，Xuzhou 221008，Jiangsu，China）

An improved algorithm of sensorless control based on square wave signal injection for interior permanent magnet synchronous motor was proposed，which could effectively enhance the bandwidth of sensorless control system.The traditional sine wave signal was replaced by square wave signal，and injection frequency is up to switching frequency，the current and feedback current induced by signals of high frequency were obtained through proposed arithmetic operation without any filters.Signal processing was simplified and dynamic response speed of system was enhanced.The validity and superiority were verified by simulation and experimental results.

permanent magnet synchronous motor；high frequency square wave signal injection；sensorless control；bandwidth；arithmetic operation

TM341

A

10.19457/j.1001-2095.20170203

2016-05-24

修改稿日期：2016-09-12

国家“十三五”重点研发计划“煤矿深井建设与提升基础理论及关键技术”（2016YFC060096）

薛映霞（1992-），女，硕士研究生，Email：853869152@qq.com