中职建筑专业中《水准测量原理》的教学方法研究

马勇

摘 要：﹤水准测量原理﹥是建筑专业课程《建筑测量》里面的一节知识，主要介绍了水准测量的基本原理及高差法、仪高法公式的应用讲解，书上仅仅用了一页的文字就讲完了，然而学生学习起来非常吃力，对公式的由来根本没法弄懂，导致很多学生学习了公式也不知道怎么用，特别是一旦已知条件和未知条件进行了互换，学生就无从思考。为了让学生能轻松弄懂水准测量的基本原理，我在教学中不断探索和总结，把本节知识与学生的实践操作结合起来，研究出了一些教学方法。

关键词：中职 水准测量原理 教学方法 研究

一、理论联系实际讲解水准测量的原理，使抽象的知识形象化

教材上用了一大段文字说明了水准测量的原理：是指利用水准测量提供的一条视线水平的原理，照准两点的水准尺，读取水准尺上的读数，根据一个点的高程推算出另外一个点高程的过程。我们在讲解的时候可以找三个学生，一人在A点架设水准尺，一人在B点架设水准尺，一人在中间架设水准仪，望远镜分别照准A点和B点得到A点和B点的读数，然后根据A点的高程推算出B点的高程就是我们的水准测量的原理。学生通过观察三个同学的操作，很容易就弄懂而且记住了水准测量的原理。

二、以图形为载体，结合实际推导出高差法的计算公式

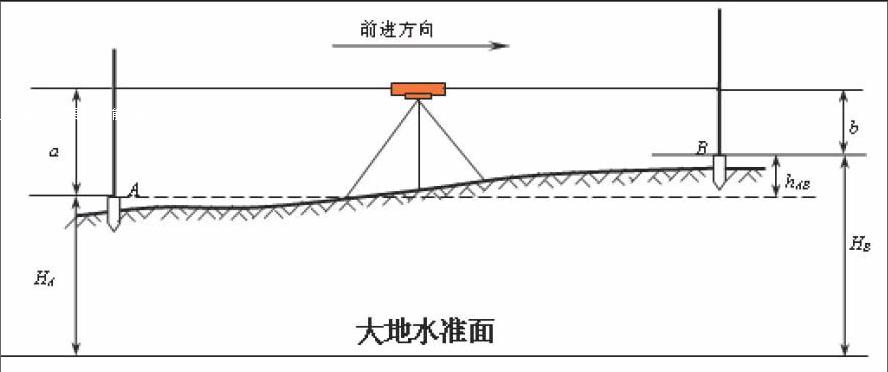
教材上直接给出了高差法的公式：，，但是学生根本不知道这个公式是怎么来的，在使用时也就只能生搬硬套，不能活学活用。我们在讲解的时候结合上图，首先让学生弄懂绝对高程的含义和高差的含义。绝对高程是指地面点到大地水准面的铅垂距离，高差是指地面上两点之间的高程之差。可以发挥学生的思维能力，让学生先思考上图中高差与两者读数和高程的关系，然后我们根据水准测量的原理，进行详细的讲解：在A、B两点架立水准尺，在中间架设水准仪，望远镜照准A点可以读出A点的读数a，照准B点可以读出B点的读数b，从图上可以看出读数a和b之差就是B点相对于A点的高差，从而推出：。再如图，根据高差的含义可得，B点高程与A点高程之差就是B点相对于A点的高差，从而推出：。这样子推出高差法的计算公式，在学生脑海里留下了较深的印象。也让学生弄懂了为什么是这两个

公式。

三、以图形为载体，结合实际推导出仪高法的计算公式

同学们稍微认真观察可以看出图中有一个比较特殊的地方，就是所有的点到大地水准面的铅垂距离加上该点的读数都是水准仪视线的高度，这样我们就可以推导出仪高法的计算公式。我们要为这个共有的视线高程单独用Hi来表示，这样就得到了公式：，，……。

四、分析高差法和仪高法的区别和联系

那么高差法和仪高法在工程当中要怎么选择呢？我们可以让学生先思考，找到各自的特点。然后进行总结归纳：高差法主要用于两个点之间求高差和高程，架设一次仪器可以计算出一个点的高程；而仪高法架设一次仪器可以计算几个未知点的高程或读数。我们要根据工程实际选择适合的计算方法，使得计算过程尽量简单方便。

五、以工程实例为载体，进一步理解水准测量原理中公式的应用

举例：张小强利用水准仪测得A点读数为1.028m，B点读数2.415m，B点高程为32.643m，求A点的高程及B点相对于A点的高差。

解：a=1.028m，b=2.415m，HB=32.643m

∵ hAB=a-b=1.028-2.415=-1.387m

又∵hAB=HB-HA

∴HA=HB-hAB=32.643-（-1.387）=34.030m

答：A点的高程为34.030m，B点相对于A点的高差为-1.387m。

六、适时课堂练习，巩固对水准测量原理的知识的掌握

课堂练习：李明利用水准仪测得A点读数为2.045，B点比A点高0.310m，B点的高程为34.661m，求A点的高程、B点的读数及A点相对于B点的高差。例题讲解了还应当给学生留下充足的时间进行课堂练习，让学生通过课堂练习消化本节课所讲授的知识点。然后请一个学生上讲台展示自己所做的答案，其他同学一起点评同学的答案是否正确，老师再对学生的课堂练习进行必要的讲解，加深学生對知识点的掌握。

中职教育就应当“以学生为主体，教师为主导”，充分发挥学生的积极性和主动性，理论联系实际，让学生多动手、多动脑，熟练掌握知识点并能够正确应用到工程实际中，这样才能培养出专业本领过硬的技术性人才。