附加索对三杆张拉整体结构的影响分析

罗阿妮, 程建军, 李全贺, 李 旭, 刘贺平

(哈尔滨工程大学机电工程学院,黑龙江哈尔滨 150001)

附加索对三杆张拉整体结构的影响分析

罗阿妮, 程建军, 李全贺, 李 旭, 刘贺平

(哈尔滨工程大学机电工程学院,黑龙江哈尔滨 150001)

张拉整体结构是由不连续的受压杆构件和连续的受拉绳索组成的特殊索杆结构,它具有质量轻、刚度高、材料利用率高的特性。研究对三杆张拉整体结构,通过添加附加索来拓展其稳定构型范围。首先,通过结构的力平衡分析,获得添加附加索前后结构保持稳定构型的扭转角度取值范围。然后根据节点坐标与连接矩阵求取构件向量并建立结构的平衡矩阵。最后通过MATLAB仿真编程分析验证了添加附加索后三杆张拉整体结构的稳定构型,范围从基本构型的两个单值角扩展到以这两个角为边界的闭区间域。

张拉整体结构;稳定性;力密度法

0 引 言

张拉整体结构是由不连续的受压构件和连续的受拉绳索组成的特殊索杆结构[1],它由美国人Fuller[2]在20世纪60年代首先提出。它具有造型优美、质量轻盈、受压构件非连续性等优点[3]。张拉整体结构的提出,扩展了人们对结构连接方面的认识。

张拉结构的最简单形式是三杆的张拉整体结构[4],其他类型结构可以由三杆张拉整体结构变换拓扑而得到[5-7]。普通三杆张拉整体结构由3根压杆、6条水平索和3条斜索组成,其中每个节点连接一个杆构件和三个索构件。结构整体外接于一个圆柱,所有节点都位于此外接圆柱的上下底面圆周上。

三杆张拉整体结构作为张拉整体结构的基础[8],引起了很多学者的分析研究。许多学者的研究都已证明,当三杆张拉整体结构的高度确定和上下底面圆的半径相等时,此结构只有2种构型,而且索杆的布置位置要求精确。这就增加了此结构的加工制造难度,构型的单一也限制了它的应用。ZHANG等[9]提出了添加附加索以增加三杆张拉整体结构构型的思想,并对这一思想的可行性进行了分析。

本研究从几何角度构型分析,并围绕结构间内部构件受力关系进一步探究获得三杆张拉整体结构添加附加索前后保持结构稳定时结构参数取值,利用力密度分析方法对所获结论进行验证。

1 三杆张拉整体结构的分析

如图1所示的普通三杆张拉整体结构中,构件内力都沿着其轴线,而构件的端部都连于节点,因此,通过节点可以确定构件的轴线方向,从而确定构件内力方向。所以,分析结构的力平衡,首先应该确定节点坐标。图中上、下底面半径分别为Ru和Rd,并且半径相同,高度为h,扭转角度为θ。

图1 三杆张拉整体结构示意图Fig.1 Sketch map of three-bars tensegrity structure

下底面节点的坐标可表示为

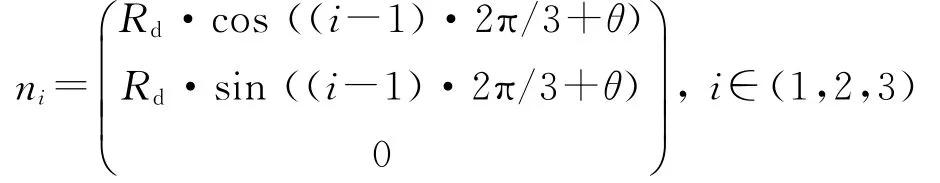
上底面节点坐标可表示为所有节点放在一起,即可形成此结构的节点矩阵:

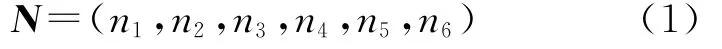
考虑到索与杆的质量很小,忽略不计。由于三杆张拉整体结构具有一定的对称性,其同类构件的长度和内力都相同。构件内力和长度的比值称为力密度,因此同类构件的力密度也相同。定义三杆张拉整体结构水平索的力密度为λ1,斜索的力密度为λ2,杆的力密度为μ;由于每个节点,连接1个杆构件和3个索构件,并且每个点相对应其他的点是关于Z轴对称的,因此各节点受力情况相同。这里只对一个节点进行力平衡分析。当图1所示的第4节点处于平衡状态时,可得

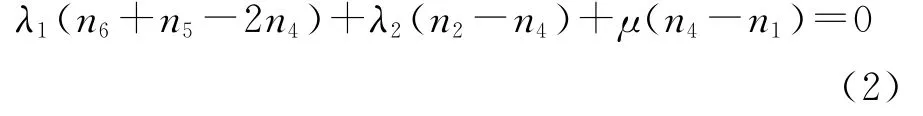
求解式(2)可得

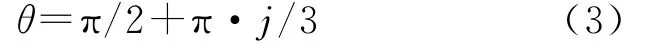
式中:j=1,2。

由式(3)可知,保持三杆张拉整体结构稳定的扭转角度θ只有150°和210°。在实际的工程安装中,由于扭转角度单一,安装精度需要进一步提高,相应地增加工程成本;同时若在外力作用导致结构变形情况下,扭转角度发生改变,结构会产生不可控制的变形失效,因此限制了张拉整体结构的应用。为了解决这一问题,下面将采用附加索来扩大保持此三杆张拉整体结构稳定时的扭转角度范围。

2 添加附加索的张拉整体结构的分析

增加附加索[9],即三杆张拉整体结构的第5、1点间,第6、2点间,第4、3点间分别增加一根索,继续分析推导,结构如图2所示。

同样的,由于对称性的原因,附加索所受到力是相同的。定义附加索力密度为λ3。推导增加附加索之后的各构件的力密度以及扭转角度变化。

以上底面的第4点为研究对象,基于以上的方法,进行分析计算。当结构在不受外力保持平衡时,即可建立类似于式(2)的平衡方程。通过平衡方程的求解,获得各力密度间关系为

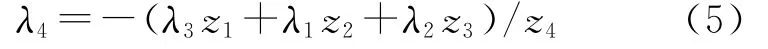
式中:

图2 添加附加索的三杆张拉整体结构Fig.2 Three-bars tensegrity structure with additional cable

这样,就获得了以水平索力密度为自变量的其他构件力密度的表达式。张拉整体结构能够保证结构稳定的必要条件是索构件和杆构件的力密度必须大于0,即λ2＞0,λ3＞0,μ＞0。将这3个限制条件带入式(3),(4),(5)中,就可以得到带有附加索的张拉整体结构扭转角度。为了便于计算,这里令水平索的力密度为1 N/cm。通过具体计算可得θ∈[150°,210°]。

3 验证及分析

3.1 构件向量

通过上面的分析,获得了添加附加索后保持结构稳定的扭转角度的取值范围。通过平衡矩阵判别方法[10]对此取值范围的正确性进行验证。要建立平衡矩阵,必须要先计算各构件向量。

根据各杆构件与节点间的关系,可得

式中:bi(i=1…3)为杆构件向量。

把杆构件向量放在一起,即可形成杆向量矩阵,即

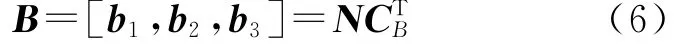
式中:CTB称为杆连接矩阵,

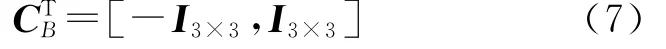
I3×3为3阶单位矩阵。

根据水平索与节点的关系,可得

斜索向量可表示为

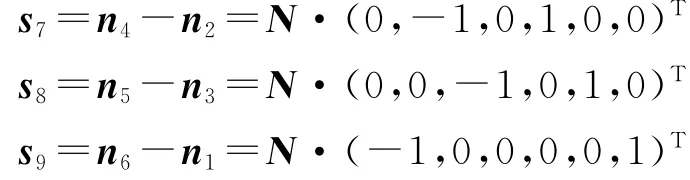
通过计算也能得到,所有的斜索长度是相等的。

3根附加索向量可表示为

能够计算得到,所有的附加索长度是相等的。把所有索构件向量放在一起,即可形成索向量矩阵

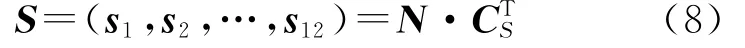
定义索连接矩阵

3.2 平衡矩阵

当图3所示的添加附加索的张拉整体结构未受外力,在节点i处于平衡状态时,有

Numerical research of CCN concentration and its parameterization scheme’s influence on a stratiform

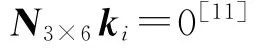
式中:

CSi为矩阵CS的第i列,为矩阵CS第i列的对角阵,CBi为矩阵CB的第i列,为矩阵CB第i列的对角阵,

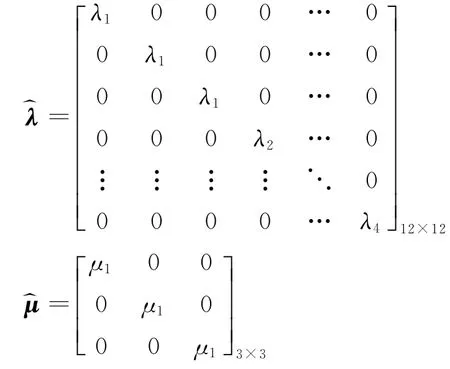
继续推导,可得:

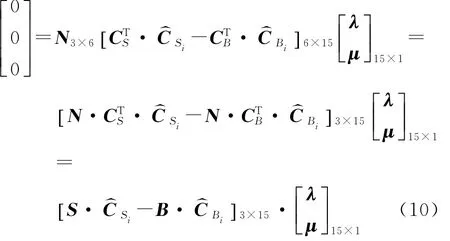
进一步推导,可得整个结构的力平衡方程:

式中A为平衡矩阵。

定义自应力模态数s和位移模态数m,有

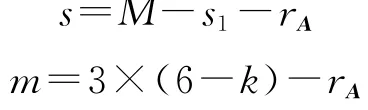
式中:s1代表固定的索数,M代表总构件数,k为约束节点的个数,rA为A的秩。根据参考文献[12],通过s和m的数值,即可判断结构的稳定性。

3.3 仿真分析

取三杆张拉整体结构的外接圆柱高度15 cm,上下端面半径20 cm。张拉结构只受到绳和索内力作用。基于式(11)编写MATLAB程序,可以得到s,m随扭转角度变化关系。当扭转角度在150°～210°变化时,自应力模态数s和位移模态数m始终为恒定值,即s=3,m=0。依据参考文献[11]可知,此结构为动定、静不定结构,因此结构稳定。通过这一分析可以证明,添加附加索增加三杆张拉整体结构的稳定构型的方法是正确的。

由图3构件长度和扭转角度的关系曲线可知,随着扭转角度的增大,附加索长度在不断地减小,长度变化量为4.4 cm。扭转角度对杆的长度变化影响很小,杆长度的变化量仅为0.52 cm。随着扭转角度逐渐增大,斜索长度也在不断地变大,整体呈一种线性关系,变化量为4.45 cm。

图3 长度与扭转角的关系Fig.3 The connection between length and tortion angle

由图4力密度与扭转角的关系知,扭转角度逐渐增大,附加索所受到的力密度也在不断地变大,最大为1.7 N/cm,整体呈一种线性关系。扭转角度逐渐增大,杆所受到力密度刚开始逐渐增大,当扭转角增加到180°时杆受到的力最大,之后扭转角继续增大,杆所受力密度逐渐减小,变化量为0.27 N/cm。扭转角度逐渐增大,斜索所受到的力密度在不断的减小,整体呈一种线性关系,力密度变化量为1.75 N/cm。

通过构件长度、力密度随扭转角的变化可以计算获得构件内力随扭转角度的变化关系。扭转角度逐渐增大,附加索所受到的力也在不断地变大,最大为37.5 N,整体呈一种线性关系。扭转角度逐渐增大,杆所受到的力刚开始逐渐增大,当扭转角增加到180°时杆受到的力最大,之后扭转角继续增大,杆所受力逐渐减小,力的变化量为9.2 N。扭转角度逐渐增大,斜索所受到的力在不断的减小,整体呈一种线性关系,变化量是37.5 N。并且,杆、斜索和附加索的长度和力密度变化以180°为对称轴,在[150°,180°]与[180°, 210°]内完全对称。

图4 力密度与扭转角的关系Fig.4 The connection between force density and tortion angle

4 结 论

通过三杆张拉整体结构进行力密度求解以及仿真分析,得到了如下成果。

(1)建立基于节点广义坐标、连接矩阵、力密度的自应力稳定的3杆12索的张拉整体结构的数学模型。

(2)以节点力平衡为出发点构建了系统的平衡矩阵,分析自应力模态和结构位移模态,获得了稳定构型的扭转角度范围[150°,210°]。

(3)在结构外包络尺寸不变的情况下,分析并获得自应力稳定构型中各构件长度、力密度随着稳定范围内扭转角度变化的函数关系。

(4)三杆张拉整体结构作为基本单元,其他张拉整体结构是在此基础上演变而成。因此,添加附加索以增加结构的稳定构型范围的方法可以考虑用于其他张拉整体结构构型研究。

[1]莫特罗.张拉整体:未来的结构体系[M].薛素铎,刘迎春,译.北京:中国建筑工业出版社,2007.

[2]FULLER R B,APPLEWHITE E J.Synergetics Explorations in the Geometry of Thinking[M].London:Collier Macmillan Publishers,1975.

[3]周一一.浅谈张拉整体结构发展的历史与趋势[J].空间结构,2013,19(4):11-17.

[4]RENÉM,吕佳,杨彬.张拉整体——从艺术到结构工程[J].建筑结构,2011(12):12-19.

[5]CSÕLLEOVÁZ.The analyses of triangular tensegrity prisms pairs[J].Procedia Engineering,2012,40: 74-78.

[6]张幸锵,袁行飞.新型三棱柱张拉整体平板结构研究[J].建筑结构,2011,41(3):24-27.

[7]陈志华,史杰,刘锡良.张拉整体三棱柱单元体试验[J].天津大学学报,2004,37(12):1053-1058.

[8]孙国鼎.张拉整体结构的形态分析[D].西安:西安电子科技大学,2010.

[9]ZHANG P,KAWAGUCHI K,FENG J.Prismatic tensegrity structures with additional cables:Integral symmetric states of self-stress and cable-controlled reconfiguration procedure[J].International Journal of Solids and Structures,2014,51(25/26):4294-4306.

[10]梁锐.基于平衡矩阵理论的张拉整体结构形态分析[D].成都:西南交通大学,2013.

[11]NAGASE K,SKELTON R E.Double-helix tensegrity structures[J].AIAA Journal,2014,53(4): 847-862.

[12]钱若军,杨联萍.张力结构的分析·设计·施工[M].南京:东南大学出版社,2003.

Analysis of three-bars tensegrity structure with additional cable

LUO Ani, CHENG Jianjun, LI Quanhe, LI Xu, LIU Heping

(College of Mechanical and Electrical Engineering,Harbin Engineering University,Harbin 150001,China)

Tensegrity was a special cable-bar structure composed of discontinuous compression bar member and continuous tension cable,which had the characters of small quality,nice mechanical properties and high material utilization.The stability range of three-bars tensegrity structure was analyzed and expanded by adding an additional cable.The torsional angle ranges of the stable structure before and after adding the additional cable were obtained by analysis of the structure force balance.According to the node coordinate and the connection matrix,the component vector was obtained and the equilibrium matrix of the structure was established.The stable configuration of three-bar tensegrity structure was verified by MATLAB simulation program,and the range was extended from the two single value angles of the basic configuration to the closed interval domain with these two angles as the boundary.

tensegrity structure;stability;force density method

TU391

A

1674-1404(2017)01-0071-05

2015-10-10.

国家自然科学基金项目(51605111,51675114);黑龙江省自然科学基金项目(11202128).

罗阿妮(1978-),女,副教授;通信作者:刘贺平(1975-),男,副教授.

罗阿妮,程建军,李全贺,李旭,刘贺平.附加索对三杆张拉整体结构的影响分析[J].大连工业大学学报,2017,36(1):71-75.

LUO Ani,CHENG Jianjun,LI Quan-he,LI Xu,LIU Heping.Analysis of three-bars tensegrity structure with additional cable[J].Journal of Dalian Polytechnic University,2017,36(1):71-75.