基于CS-GPSR的电容层析成像图像重建算法*
田 沛, 刘昭麟, 张立峰
(1.河北省发电过程仿真与优化控制工程技术研究中心,河北 保定 071003;2.华北电力大学 自动化系,河北 保定 071003)
基于CS-GPSR的电容层析成像图像重建算法*
田 沛1,2, 刘昭麟2, 张立峰2
(1.河北省发电过程仿真与优化控制工程技术研究中心,河北 保定 071003;2.华北电力大学 自动化系,河北 保定 071003)
提出将基于压缩感知(CS)理论的稀疏梯度投影(GPSR)算法应用于电容层析成像(ECT)图像重建过程中。采用离散Fourier变换(DFT)基将原始图像灰度信号进行稀疏化处理;将ECT灵敏度矩阵的各行按随机顺序进行排列,得到ECT系统观测矩阵,同时将测量电容向量的各行按相同顺序进行排列,得到观测投影向量;使用GPSR算法进行图像重建。仿真实验结果表明:基于CS理论的GPSR(CS-GPSR)算法重建图像质量明显优于LBP算法和Landweber迭代算法。本文所述算法可实现较高精度的图像重建,为ECT图像重建的研究提供了一种新的手段。
电容层析成像; 图像重建; 压缩感知稀疏梯度投影
0 引 言
电容层析成像(electrical capacitance tomography,ECT)技术发展于20世纪80年代,它基于电容敏感机理对工业管道中多相流体进行在线监测,具有非辐射、非侵入、结构简单、安装携带方便、成本低、响应速度快等优点,为化工、石油、电力、能源等现代工业生产中多相流体的在线测量提供了新的手段[1]。
典型16电极ECT系统成像过程为:数据采集系统产生一定频率的正弦电压信号并将其传送至传感器阵列的激励电极;电极阵列通过测量不同电极对之间的电容值获得测量投影信号;图像重建单元运用某种图像重建算法将管道截面处介电常数分布图像由测量投影信号重建出来。
目前ECT图像重建算法可分为非迭代算法和迭代算法两大类[2]。非迭代算法,如线性反投影算法,简单快速,但重建图像精度太低,无法满足工业要求;迭代算法,如Landweber算法,重建图像精度较高,但其收敛速度慢,影响成像的实时性。
2004年,Donoho D L和Candès E等人提出了压缩感知(compressed sensing,CS)理论[3],它突破了传统采样定理对信号带宽的限制,通过极少量的采样数据即可高精度地重建出原始信号,为信号采集技术带来了革命性的突破。该理论提出:若信号在某个变换域内是稀疏的或可压缩的,便可以使用与稀疏基不相关的随机观测矩阵对原始信号进行投影得到低维测量信号。通过求解最优化问题就能将原始信号从低维测量信号中精确重建。目前,CS理论已经广泛应用于压缩成像、雷达、通信、医疗成像等诸多领域。
本文提出将基于CS理论的稀疏梯度投影算法(CS gradient projection for spare reconstruction,CS-GPSR)应用于ECT图像重建过程中,使得重建图像更加接近于原始图像。
1 CS原理简介
CS的前提条件是信号具有稀疏性或者可压缩性[4],而实际信号往往并非稀疏信号。为了使其满足CS理论,寻找一组合适的正交变换基,对信号进行正交变换,使其成为稀疏信号或可压缩信号。
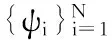
(1)
式中Ψ为N×N维正交基,ΨN×N=[ψ1ψ2…ψN];s为N×1维的系数向量。当s仅有K≪N个非零系数时,信号x在变换基Ψ上是稀疏的,稀疏度为K。
常用的稀疏基有:离散Fourier变换基(DFT)、离散余弦变换基(DCT)、离散正弦变换基(DST)、离散小波变换基(DWT)等。
CS的核心是线性测量过程,设计合适的观测系统对原始信号x进行线性观测。通过对信号x进行投影得到测量投影向量y,即
y=Φx=ΦΨs=Acss
(2)
式中 y为M×1维的观测向量;Φ为M×N维的观测矩阵,且M < N。令ACS=ΦΨ,称ACS为CS矩阵。
对于给定的y从式(2)中求出x是一个线性规划问题,由于观测信号y维数M小于原始信号x维数N,使得方程(2)为欠定方程,通常无确定解。但通过使用K稀疏的先验条件,方程(2)便有望求解。
由CS理论知,当CS矩阵ACS满足限制等距条件[5](restricted isometry property,RIP)时,便可运用多种CS重建算法将s的K个非零系数从M个测量值中准确重建,同时保证重建过程收敛。RIP条件的等价条件是观测矩阵Φ和稀疏基Ψ不相关[6]。文献[7]指出,当使用高斯随机矩阵作为观测矩阵,任意正交基作为稀疏基时,观测矩阵和稀疏基不相关,ACS可在较高概率下满足RIP条件,从而使得欠定方程(2)得以求解。
利用信号稀疏或可压缩的先验条件,最直接的方法是采用最小L0范数模型求解CS信号重构问题

xopt=Ψsopt
(3)
但由于L0范数具有非凸性,直接求解式(3)的数值计算极不稳定而且是NP困难问题[8],故各种替代模型及其对应的CS重建算法相继被提出[9],典型算法如凸松弛(最小L1范数)算法、贪婪算法、迭代阈值算法、最小全变差算法等。
2 基于CS理论的ECT图像重建
离散Fourier变换(DFT)基对于二值图像信号的稀疏效果较好,可用作ECT系统的稀疏基,对重建图像灰度信号进行稀疏化处理,即
g=ΨFFTs
(4)
式中g为N×1维重建图像灰度向量;ΨFFT为N×N维快速Fourier变换(FFT)基;s为N×1维K项稀疏系数向量。
CS理论要求观测系统对原始信号的观测过程为线性过程,ECT系统线性模型如下[10]
λ=Sg
(5)
将式(4)代入式(5)中,得到基于CS理论的ECT系统数学模型
λ=Sg=SΨFFTs=AECTs
(6)
式中 λ为M×1维测量电容向量经归一化处理后的测量投影向量;S即为M×N维的ECT系统观测矩阵;AECT为ECT系统CS矩阵;λ即为ECT采样系统通过观测矩阵S对原始图像灰度信号g进行观测得到的观测投影向量。
16电极ECT系统可以得到的独立测量数M=16×15/2=120,为保证ECT系统成像精度,成像区域采用正方形网格剖分,像素数N=812。由CS理论可知,为使得重建图像灰度向量g的N个像素灰度值可以由测量投影向量λ的M个独立测量值精确重建,ECT系统CS矩阵AECT必须满足RIP条件,即观测矩阵S为高斯随机矩阵。但由于ECT系统硬件条件和固有采样方式的限制,实现测量数据的随机观测十分困难。为提高观测矩阵S的随机性,故本文将原观测矩阵S的各行向量按高斯随机顺序重新排列得到新的随机观测矩阵Snew,使其具有一定的随机性,将测量投影向量λ各行以相同的顺序重新排列得到新的投影向量λnew。这样,随机观测矩阵Snew和稀疏基ΨFFT具有不相关性,在一定概率下满足RIP条件。
文献[11]指出,当观测矩阵Snew和稀疏基ΨFFT不相关时,最小L1范数问题和最小L0范数问题具有相同的解。最小L1范数问题为凸优化问题,可方便地转化为线性规划问题进行求解
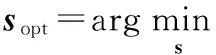
gopt=ΨFFTsopt
(7)
在求解式(7)过程中,将约束凸优化问题转化为无约束的凸优化问题,同时使用L1范数正则化模型[12]可有效克服ECT系统病态性
gopt=ΨFFTsopt
(8)
本文使用GPSR算法[13]对式(8)进行求解,实现ECT系统图像重建。
GPSR算法是用于CS信号重构的一种经典算法,通过把稀疏系数向量s分按正负元素分为两部分(即s=u-v,其中u=(s)+=max(0,s)≥0,v=(-s)+≥0),如式(9)的L1范数正则化模型可被转化成为如式(10)的二次规划问题

(9)
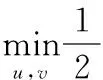
(10)
式中 1N=[1,1,…,1]T为N维元素全部为1的列向量,经过推演,可变形为如式(11)的非负约束集上的二次规划问题
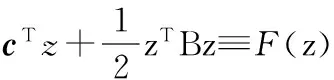
s.t.z≥0
(11)
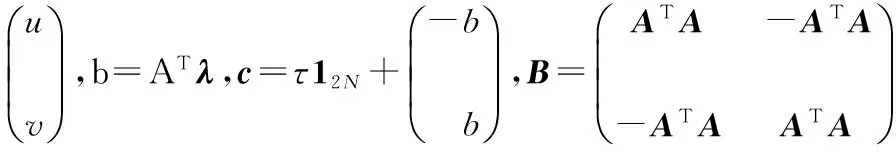

GPSR算法的迭代步骤如下:
初始化:选定初始值z(0),选择参数β∈(0,1)和μ∈(0,1/2),令迭代步数i=0。
1)计算步长:按公式计算α0;

经GPSR算法所重建出的图像灰度值经归一化处理后g∈[0,1],并非二值图像。本文使用最优阈值方法,基于式(12),即考虑可能的阈值,计算选取误差最小时的阈值作为最优阈值,对图像进行二值处理
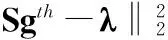
(12)
式中 gth为阈值处理后的图像灰度值。
3 实验结果与分析
本文以油气两相流为研究对象,设定了三种典型流型进行仿真实验,其中油和气的相对介电常数分别为2.6和1,使用COMSOL3.5a有限元软件获得仿真测量电容值数据,使用Matlab软件进行ECT图像重建,成像区域采用正方形网格剖分为812个像素。
仿真过程中,采用LBP算法、Landweber算法及本文提出的基于CS理论的GPSR算法分别进行图像重建,获得初始重建图像,如图1所示;为了使重建图像更好地接近于原始图像,采用最优阈值法对重建图像进行后处理,获得二值图像,如图2所示。
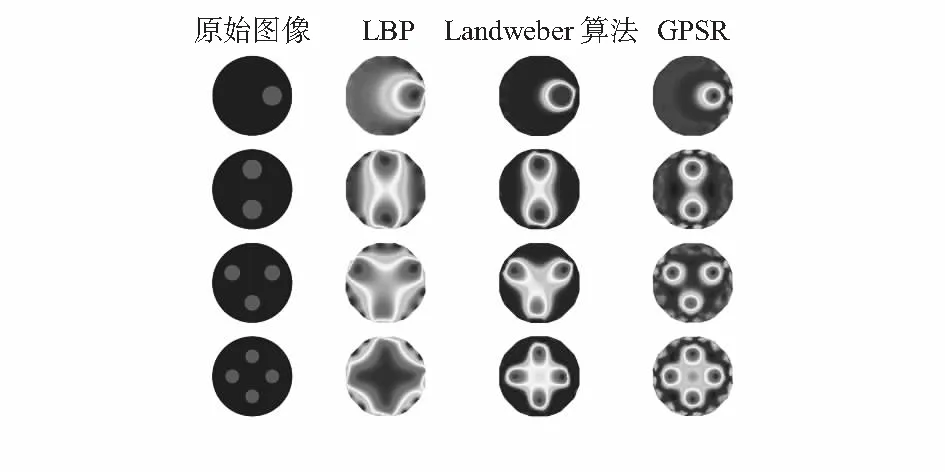
图1 初始重建图像

图2 后处理重建图像
由图1可见,相较于LBP算法和Landweber算法重建图像,基于CS理论的GPSR算法能够较高精度地对场域中的各种流型进行重建。GPSR算法能够较清楚地重建场域内物体的位置信息和边缘信息,重建图像中,物体分布准确、边缘规则、区分度好、形状保真度高;而LBP算法和Landweber算法重建图像中,重建物体发生形变、伪迹明显、不能清楚地区分。由流型3和流型4的重建图像可以看出,对于较为复杂的流型,LBP算法重建图像完全失真,Landweber算法重建图像精度较低,而GPSR算法依然可以实现较高精度的图像重建。由图2可见,对三种算法重建图像进行最优阈值处理之后,其重建图像精确度均有明显改善,可以看出GPSR算法重建图像更加接近真实分布。
为定量评价重建图像质量,采用相对误差(RE)和相关系数(CC)作为评价指标,其定义分别为
(13)
(14)

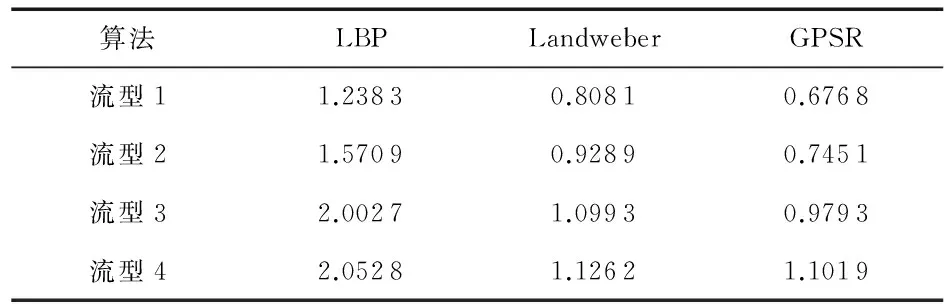
表1 初始重建图像相对误差(RE)
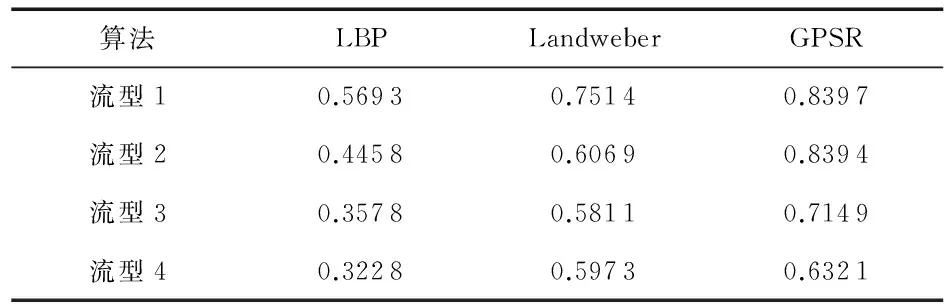
表2 初始重建图像相关系数(CC)

表3 后处理重建图像相对误差(RE)
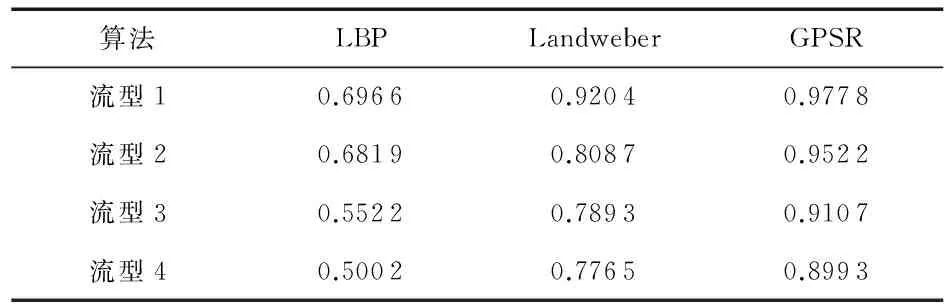
表4 后处理重建图像相关系数(CC)
分析表1~表4中三种算法重建图像的性能指标可知,对比LBP算法、Landweber算法和基于CS理论的GPSR算法重建图像的各项指标,GPSR算法重建图像的相对误差最小,而相关系数最大,说明GPSR算法重建效果优于LBP算法和Landweber算法,重建图像精度较高,与真实分布更加接近。通过使用最优阈值法后处理,三种算法重建图像精确度均有明显改善,但GPSR算法重建图像精度仍优于LBP算法和Landweber算法。故将本文所论述的算法应用于ECT图像重建中,可获得较高精度的重建图像。
4 结 论
本文提出将基于CS理论的稀疏梯度投影(CS-GPSR)算法应用于ECT图像重建过程。由于CS理论可以在较少观测数据的情况下精确重建原始信号,故应用于ECT图像重建中可以较好地解决ECT系统欠定性问题;同时GPSR算法可以对场域内物体的位置信息和边缘信息进行有效地重建,故重建图像精度较高。仿真结果表明:该算法成像精度高,适合应用于ECT图像重建过程中,为ECT图像重建提供了一种新的途径和手段。
[1] 高彦丽,章勇高,邵富群,等.电容层析成像技术中图像重建算法的发展及研究[J].传感器与微系统,2007,26(10):9-11,14.
[2] 王 挺,范文茹,郝魁红,等.平面式电容传感器阵列激励模式研究[J].传感器与微系统,2012,31(9):71-74.
[3] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[4] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.
[5] Candès E.The restricted isometry property and its implications for compressed sensing[J].Acadèmie des Sciences,2006,346(1):589-592.
[6] Baraniuk R G.A lecture on compressive sensing[J].IEEE Trans on Signal Processing Magazine,2007,24(4):118-121.
[7] Baraniuk R,Davenport M,Devore R,et a1.A simple proof of the restricted isometry property for random matrices[J].Constructive Approximation,2008,28(3):253-263.
[8] Natarajan B K.Sparse approximate solutions to linear system-s[J].SIAM Journal on Computing,1995,24(2):227-234.
[9] 李 佳,张立峰,田 沛.基于Kalman滤波的ECT图像重建算法[J].传感器与微系统,2015,34(8):128-130.
[10] Dickin F J,Wang M.Electrical resistance tomography for process applications[J].Meas Sci Technol,1996,7(3):247-260.
[11] Chen S S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Review,2001,43(1):129-159.
[12] 王丕涛,王化祥,孙犇渊.基于l1范数的电容层析成像图像重建算法[J].中国电机工程学报,2015,35(18):4709-4714.
[13] Figueiredo M A T,Nowak R D,Wright S J.Gradient projection for sparse reconstruction:Applicationto compressed sensing and other inverse problem[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(4):586-597.
Image reconstruction algorithm for electrical capacitance tomography based on CS-GPSR*
TIAN Pei1,2, LIU Zhao-lin2, ZHANG Li-feng2
(1.Hebei Engineering Research Center of Simulation & Optimized Control for Power Generation,Baoding 071003,China; 2.Department of Automation,North China Electric Power University,Baoding 071003,China)
Gradient projection for spare reconstruction(GPSR)algorithm based on compressed sensing(CS) theory is applied to electrical capacitance tomography(ECT)image reconstruction. Use orthogonal basis of discrete Fourier transformation(DFT),the gray signals of original images can be transformed into sparse signals.Measurement matrix of ECT system is designed by rearranging the rows of the sensitivity matrix of ECT in a random order and the measurement projection vector is designed by rearranging the rows of the capacitance value vector in the same order.The GPSR algorithm is used for image reconstruction.The simulation results show that the quality of the reconstructed images are better than the corresponding images obtained by the LBP algorithm and the Landweber algorithm.The proposed algorithm can achieve higher precision of ECT image reconstruction and provide a new method for the research of ECT image reconstruction.
electrical capacitance tomography(ECT); image reconstruction; compressed sensing gradient projection for spare reconstruction(CS-GPSR)
10.13873/J.1000—9787(2017)03—0136—04
2016—04—07
国家自然科学基金资助项目(51306058);中央高校基本科研业务费专项项目(2014MS142)
TP 391
A
1000—9787(2017)03—0136—04
田 沛(1957-),男,教授,主要从事现代传感技术,多源信息融合和软测量,数字图象处理及机器视觉研究工作。
刘昭麟, 通讯作者,E-mail:liu_zhaolin1991@163.com。

