滴灌灌水器迷宫流道结构对泥沙运动的影响

喻黎明 徐 霞 杨启良 吴永栋 白晓军

(1.昆明理工大学现代农业工程学院， 昆明 650500； 2.长沙理工大学水利工程学院， 长沙 410114；3.青海省水利水电勘测设计研究院， 西宁 810001)

滴灌灌水器迷宫流道结构对泥沙运动的影响

喻黎明1徐 霞2杨启良1吴永栋3白晓军3

(1.昆明理工大学现代农业工程学院， 昆明 650500； 2.长沙理工大学水利工程学院， 长沙 410114；3.青海省水利水电勘测设计研究院， 西宁 810001)

采用基于颗粒动力学理论的欧拉-拉格朗日固液多相湍流模型，选用夹角、上底宽、齿高、齿尖参差量、流道宽等五因素四水平组成16个迷宫流道模型，进行水沙运动CFD-DEM耦合数值模拟，分析沙粒群通过率、速度下降百分数、沙粒群运动和分布规律。结果表明：沙粒群通过率能有效描述迷宫流道的抗堵塞性能，沙粒群通过率与沙粒速度下降百分数呈负相关，沙粒群整体速度下降是影响迷宫流道内沙粒通过率的核心因素；沙粒速度的变化取决于流道内水流运动特性，而夹角、流道宽是影响水流特性的主要流道结构参数，其中夹角具有显著性影响；较优结构中可使沙粒始终受曳力牵引，大部分沙粒运行于主流区中，保持较高的运动速度，速度下降较小，动能损失少，通过率高，减少了被堵塞的机率；该方法统计了沙粒群运动及分布规律，从微观角度分析迷宫流道内沙粒运动，将有效提高迷宫流道结构设计效率。

滴灌灌水器； 迷宫流道； 结构参数； 数值模拟； 通过率

引言

迷宫流道滴头是目前使用最为广泛的一种滴头[1]，但结构复杂、尺寸微小使水中泥沙颗粒易在流道内沉积，最终导致堵塞[2]，因而滴头堵塞问题是众多专家的研究热点。NAKAYAMA等[3]和TAYLOR等[4]认为滴头的堵塞是流道几何参数、形状参数等多个因素综合作用产生的结果，认为滴头的结构设计最重要。LI等[5]、张俊[6]、谢巧丽等[7]通过正交试验分析了齿间距、夹角、齿高、流道深等迷宫流道结构参数对迷宫流道抗堵塞能力的影响，得出夹角对抗堵塞能力影响最大且显著。王文娥等[8]认为，在齿形流道所有参数中对颗粒分布影响程度由大到小的顺序是：齿角度、齿间距、流道深度、齿高。以上研究均是通过宏观的试验，分析找出结构参数对堵塞影响的程度和顺序。而魏正英等[9]通过计算流体动力学(Computational fluid dynamics, CFD)数值模拟的方法，针对消除流速较小的滞止区域，提出了主航道抗堵优化设计思路。孟桂祥等[10]认为，在灌水器流道设计时要加强水流的紊流程度，以增强流道的自清洗功能。

上述学者分析了部分结构参数对堵塞的影响，但分析方法上，有根据物理模型测试分析具体的结果，而内在的原因不明确，有从水流运动分析，根据水流运动规律推算沙粒的运动和分布，尤其是CFD使用欧拉-欧拉两相流模型或更简单地使用拉格朗日坐标系下弥散相模型(Discrete phase model， DPM)，将沙粒当成固相流体研究，忽视了沙粒本身及壁面所具有的碰撞以及对流场反作用的影响。本文采用CFD-DEM耦合计算方法，追踪所有进入流道的沙粒在每个时刻的运动特性和具体位置，揭示结构参数变化对滴头内沙粒运动与分布的影响，为迷宫流道抗堵塞设计提供理论依据。

1 数值模拟方法

1.1 物理模型及网格划分

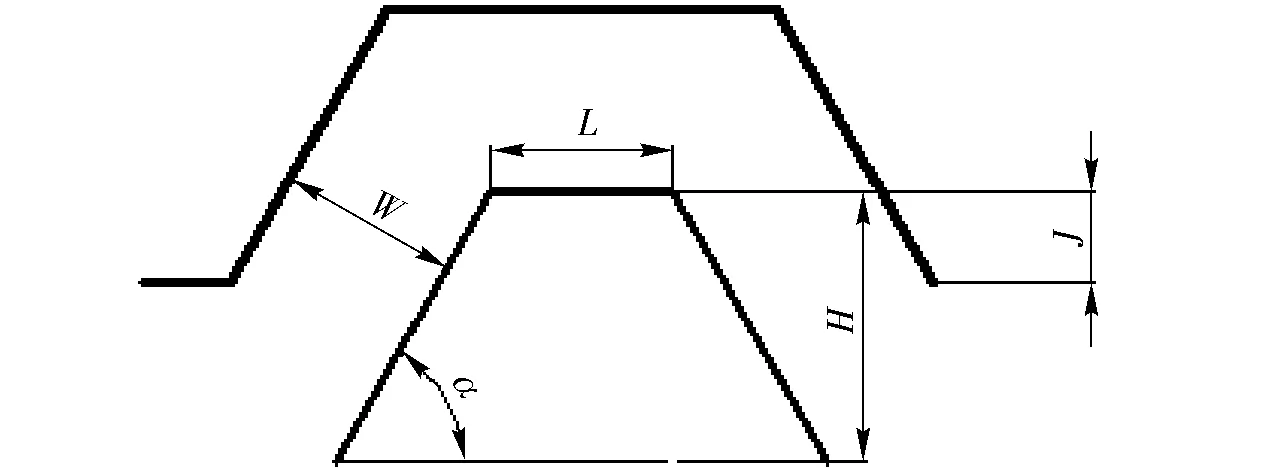
图1 流道结构示意图Fig.1 Structure sketch of flow path of emitter

图1为灌水器结构示意图，其主要参数有：流道宽W、斜边和底边夹角α、齿高H、上底宽L、齿尖参差量J，流道单元数为8 个，流道深D为0.8 mm，进出口长度均设为1 mm，如表1所示。按五因素四水平设计正交试验L16(45)，共计组合成16种灌水器。

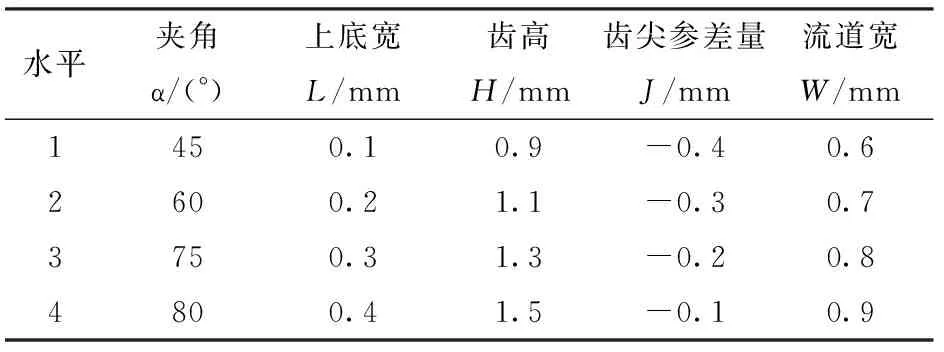
表1 试验因素水平Tab.1 Factors and levels of experiment

1.2 网格划分和数值模拟方法

采用的CFD和DEM软件分别为FLUENT 12.0、EDEM 2.1，计算域为从灌水器的进口到出口，在计算域内利用GAMBIT划分网格，采用六面体网格单元，网格单元长度为0.1 mm左右，网格单元数为(4～8)×104个单元。采用FLUENT软件默认的标准壁面函数法对流道壁面处理，数值计算采用有限体积方法及离散控制方程，对流项等各参数的离散均采用二阶迎风格式，速度与压力的耦合采用SIMPLE算法求解，收敛精度为10-4。

流道内水流可视为粘性不可压缩流体，常温下定常流动，本文采用定常流动假设进行模拟，考虑重力作用，忽略表面张力影响。目前，滴头雷诺数Re在78～1 284之间， PAULAU等[11]发现层、紊流转变发生在雷诺数Re为200～350时，远小于常规平直流道的临界雷诺数。因此，连续相的模拟采用标准k-ε紊流模型，其计算公式参照文献[12]。

水相连续性方程和动量方程为

(1)

(2)

其中

Fdci=-∑Fdc,di

工作压力为50 kPa，沙粒粒径为0.065 mm，沙粒体积分数为1%，属于稀相流，采用拉格朗日耦合方法，沙粒的移动、沙粒与沙粒之间的碰撞、沙粒与壁面之间的碰撞以及沙粒运动对周围连续相的作用、能量和动量交换均采用离散方法模拟，沙粒之间及沙粒与壁面之间的碰撞不会发生显著的塑性形变，属于硬沙粒接触，是湿沙粒接触模型，本文采用“Hertz-Mindlin (no slip) built-in”模型计算，主要考虑曳力和重力，其他附加力如压力梯度力、虚假质量力、升力等与前者相比数量级较小，故不予考虑[13]，所采用的模型参数参照文献[14]。

沙粒相连续性方程和动量方程[17]为

(3)

(4)

其中

沙粒间法向力Fn计算式[15-16]为

(5)

其中

式中E*——等效弹性模量R*——等效沙粒半径k——重叠量ν1——沙粒1的泊松比ν2——沙粒2的泊松比E1——沙粒1的弹性模量E2——沙粒2的弹性模量

(6)

其中

(7)

式中m*——等效质量β——阻力系数Sn——法向刚度vrel——相对速度m1——沙粒1质量m2——沙粒2质量

沙粒间切向力Ft的计算式为

Ft=-Stδ

(8)

其中

(9)

(10)

式中δ——切向重叠量St——切向刚度G*——等效剪切模量G1——沙粒1的剪切模量G2——沙粒2的剪切模量

(11)

计算中的滚动摩擦是很重要的，它可以通过接触表面上的力矩来说明，即

Ti=-μrFnRiωi

(12)

式中μr——滚动摩擦因数Ri——质心到接触点间的距离ωi——接触点处物体的单位角速度矢量

具体的CFD与DEM双向耦合过程如图2所示。CFD求解连续相后，获得流场信息，通过曳力模型转化为作用在沙粒上的流体曳力，计算结果传递给DEM，由DEM计算沙粒受力情况，给出沙粒新的位置和速度等信息及对流场的反作用力，计算结果传回CFD，由CFD更新流场并产生对沙粒新的受力情况，循环往返，二者通过一定的模型进行质量、动量和能量的传递，实现耦合[17]。

图2 CFD-DEM耦合求解过程Fig.2 Solution process of CFD-DEM

1.3 通过率

沙粒通过率高表明大多数沙粒能穿过流道，不会停留淤积在流道内而造成堵塞，也即通过率越高，滴头的抗堵塞能力越强。沙粒通过率计算式为

(13)

式中Nt——设定时间内通过流道的总沙粒数Nz——设定时间内在流道内出现的总沙粒数Tmin——沙粒通过流道所需要的最短时间T——计算总时长

1.4 速度下降百分数

能量公式为

(14)

式中M——沙粒质量，kgV——沙粒的运动速度，m/s

速度下降百分数为

(15)

式中Vi——沙粒投放时初始速度，m/sVa——沙粒通过流道的平均速度，m/sN——速度下降百分数，%

所有通过的沙粒，都可由EDEM输出运行轨迹线长度和运行时间，根据自编程序可计算出单个沙粒平均速度和沙粒群的平均速度。

2 结果与分析

2.1 结构参数与通过率的正交试验分析

正交试验结果和方差分析结果分别如表2、3所示，由极值分析和方差分析可知，各结构参数对沙粒通过率都有影响。其中夹角对通过率影响最大且显著，其他依次为流道宽、齿尖参差量、上底宽、齿高，但都不具有显著性。编号为5、14、16号流道沙粒通过率较高，而9、10号流道通过率最低。该模拟结果与喻黎明等[18]采用混水试验方法和LI等[5]参照“短周期堵塞测试程序”针对正交试验模型进行的沙粒抗堵塞试验结论一致，该结果表明，采用沙粒通过率能有效描述迷宫流道的抗堵塞性能。对通过率具有显著性影响的原因是夹角对水力性能具有显著性影响，流道夹角的增加加大了水流方向改变的程度，从而加大了水流的紊流程度，使得流道内局部水头损失系数增大，流道内水流总体速度下降，水流携带能力下降从而导致沙粒的运动速度下降，进而影响到沙粒通过率。

2.2 结构参数对沙粒速度和通过率的影响

图3为各结构参数变化与沙粒群通过率、沙粒群平均速度下降百分数的关系。随着各结构参数的变化，沙粒通过率与沙粒平均速度下降百分数呈负相关，即总体变化趋势相反，两趋势线发生相交。通过率越低对应的速度下降百分数越高，也证明了速度下降降低了沙粒的动能，会促使沙粒沉淀，无法通过。

表2 灌水器流道结构参数与沙粒通过率正交试验结果Tab.2 Orthogonal test result of emitter structure parameters and pass rate of sand

表3 灌水器流道结构参数对流道中沙粒通过率影响的方差分析Tab.3 Variance analysis of effect of low path parameters on pass rate of sand

注：*表示差异显著(p<0.10)，F临界值为2.490。

2.3 流体流场与沙粒分布

图4为正交试验中通过率较高的5号流道和通过率较低的9号流道当工作压力为50 kPa时流道宽1/2位置沿水流方向的速度分布图，两者的最大速度和最小速度相同，分别为2.4、0.2 m/s，齿尖附近流速最大，靠近壁面和漩涡区中心处流速最低。5号流道中流场流速分布较为均匀，低速区面积较小且主流区流线流畅，颜色较亮即速度较高部分的区域连贯，迎水面具有较高的速度，背水面速度较低，存在局部的涡旋区；而9号流道，高速区仅存在于齿尖部位，且成点状分布，两高速区之间有较大的

图3 结构参数与沙粒群通过率、速度下降百分数的关系Fig.3 Relationships between structure parameters and pass rate of sand and percentage decrease in speed

图5 沙粒分布Fig.5 Distributions of sand

图4 水流速度分布Fig.4 Distributions of water velocity

速度差，低速区分布面积较大，主要分布在底部和顶部，距离主流区较远，易形成漩涡区。

图5为5、9号流道输入输出动态平衡后沙粒在流道内的分布，9号流道中沙粒分布范围明显比5号流道紊乱很多，在迎水面的拐角处沙粒集中现象非常明显，最快穿过两流道沙粒的运行时间分别为0.05、0.02 s，但9号流道内存留时间大于0.3 s的沙粒占6.71%，大于0.2 s的沙粒占11.31%，大于0.1 s的沙粒占17.62%，而5号流道中沙粒留存数量较少，单个沙粒的轨迹接近沙粒群整体运行轨迹线，光滑整齐，在迎水面出现了少量的堆积现象，且所有沙粒都在0.1 s内穿过流道。

图6为两流道第3、4流道单元上速度线和沙粒分布，红线为2.0～2.4 m/s流速区域，绿线为1.6～2.0 m/s流速区域。5号流道中，红线、绿线形成的区域连贯了整个流道，从入口到出口，大部分的沙粒都在绿线内运动；而9号流道只有绿线连贯了入口到出口，且红线所标示的高速区域形成了独立的封闭区域，中间形成了断层，大部分的沙粒都运动于绿线区域之外。从沙粒分布区域分析，两者都存在迎水面沙粒分布较多的情况，只是9号流道中迎水面存在显著的沙粒积聚现象。

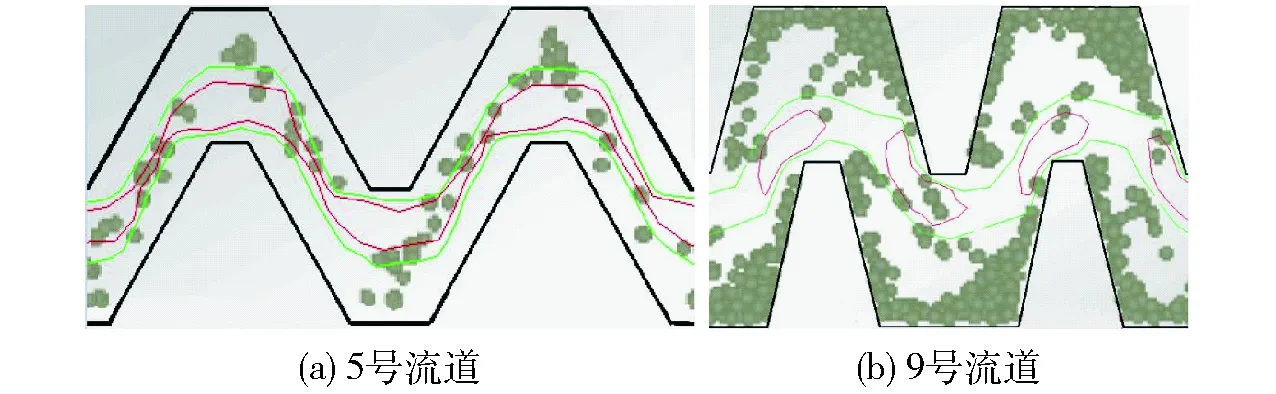
图6 第3、4流道单元速度线和沙粒分布Fig.6 Distributions of sand in the third and fourth flow unit

从沙粒受力分析，沙粒在流道中运行，主要在水流曳力作用下运动，在5号流道中，红线形成的主流区连贯整个流道，沙粒在主流区内始终受到曳力的牵引，沙粒在主流区内运动，较少脱离曳力作用，因而难以被水流抛出去，保持较高的速度运行，最终容易穿过流道；而9号流道中，形成的高速区只出现在齿尖附近，沙粒在齿尖附近获得曳力的牵引，获得较高速度，当沙粒离开高速区，进入绿线区域时，沙粒的运行速度高于水流速度，沙粒所受到的力主要为水流的阻力和本身具有的高速惯性力，沙粒较容易被抛出去，抛出去的沙粒保持了在高速区加速时所获得的运动方向，从而使得迎水面的沙粒较多、较集中，导致沙粒之间、沙粒与壁面之间在碰撞作用下，进入旋涡区，被带到背水面，形成了迎水面沙粒较多、背水面沙粒较少的现象。

这种现象与魏正英等[19]和喻黎明等[20]通过PTV追踪沙粒在流道主流区和漩涡区运动的规律非常相似，均发现当沙粒在主流区时，沙粒能获得较高的速度，且保持时间较长，更易通过，当沙粒在漩涡区时，运动速度下降而难以通过。

2.4 沙粒群分布规律统计

表4是1 s内穿过5、9号流道的沙粒群特性，沙粒的释放速度与水流速度相同，且5号流道中投放的数量更多，但进入旋涡区的沙粒仅为21.90%，而9号流道进入漩涡区的沙粒为84.58%。进入漩涡区沙粒越少，参与漩涡区循环的次数就越少，沙粒总体的运行路程越短，运行时间越少，运行速度就越快，5号流道沙粒的运行速度接近于9号流道中的4倍，即使部分沙粒进入了漩涡区，参与了循环，最终都以较高的速度运行。5号流道中，沙粒平均运动速度相比入口初始速度下降了16.54%，而9号流道中，沙粒平均运动速度相比入口初始速度下降了64.37%，下降速度较大，能量损失较多，降低了沙粒的通过率，从而降低了灌水器的抗堵塞能力。

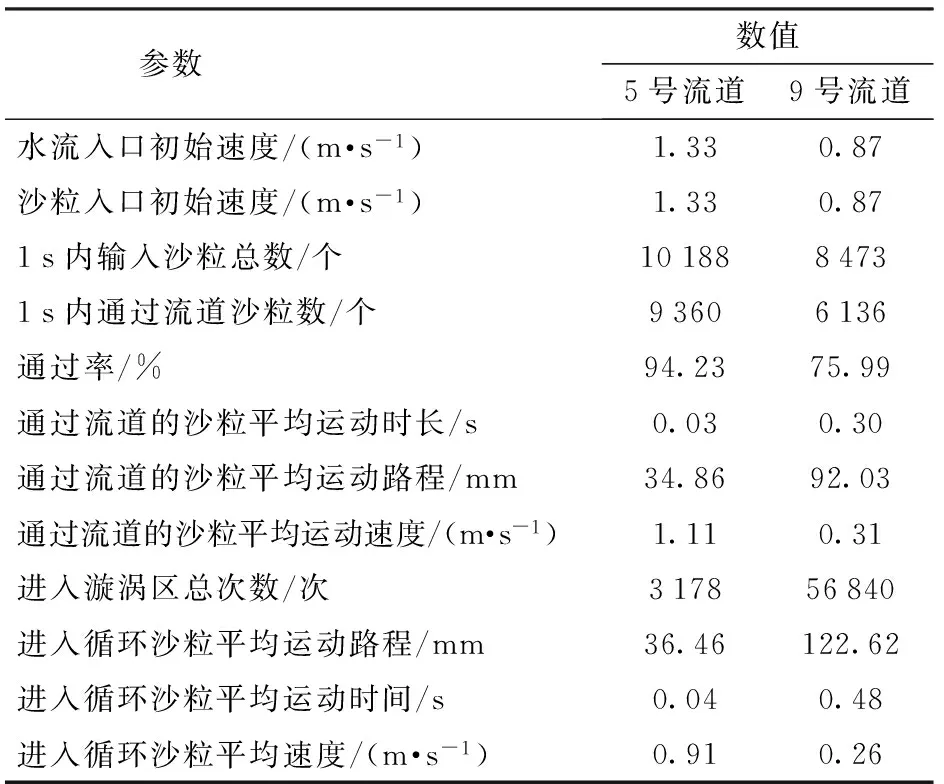
表4 1 s内穿过流道的沙粒群特性Tab.4 Characteristics of sand group passing flow channel in 1 s

通过率为70%～80%之间的只有试验9、10，两者沙粒平均速度下降百分数平均为65.74%，通过率为80%～90%之间、90%～100%之间都为7个，平均速度下降百分数分别为36.92%和23.33%，由此可知，沙粒通过率与沙粒平均速度下降百分数呈负相关，沙粒通过率越高，沙粒平均速度下降百分数越小，沙粒在流道中损失的能量就越少，而沙粒在流道内运动时平均速度下降得越大，能量损失越多，待沙粒能量损失到一定程度时，其速度小到不足以支撑其通过流道，从而在流道中循环运动或最终在流道中沉淀，随着这种沙粒数量增加将造成流道堵塞，因此需要尽量保持沙粒在流道内较高速运动，减少其在流道内的速度损失。

3 结论

(1)正交试验表明，迷宫流道结构参数的变化对沙粒通过率影响程度由大到小顺序是：夹角、流道宽、齿尖参差量、上底宽、齿高，其中只有夹角具有显著性影响。

(2)代表性较优和较差的结构中，流场存在较大的差别，较优结构中的沙粒始终受曳力的牵引，大部分沙粒运行于主流区中，而较差结构中的沙粒反复受水流曳力和阻力作用，易出现大部分沙粒脱离主流区运动的现象。

(3)沙粒通过率能有效描述迷宫流道的抗堵塞性能，沙粒通过率与沙粒平均速度下降百分数呈负相关，当沙粒速度下降百分数较大时，通过率较低，当沙粒速度下降百分数较小时，通过率较高。沙粒通过率与沙粒平均速度下降百分数为灌水器流道结构设计提供了有效方法。

1 WEI Q,SHI Y,DONG W, et al.Advanced methods to develop drip emitters with new channel types[J]. Applied Engineering in Agriculture, 2006, 22(2):243-250.

2 CAMP C R.Subsurface drip irrigation: a review[J].Transactions of the ASAE,1998,41(5):1353-1367.

3 NAKAYAMA F S, GILBERT R G, BUCKS D A. Water treatments in trickle irrigation system[J]. Journal of the Irrigation & Drainage Division, 1978, 104(1):23-34.

4 TAYLOR H D, BASTOS R K X, PEARSON H W, et al. Drip irrigation with waste stabilisation pond effluents: solving the problem of emitter fouling[J]. Water Science & Technology, 1995, 31(12):417-424.

5 LI Guangyong，WANG Jiandong，ALAM M，et al.Influence of geometrical parameters of labyrinth flow path of drip emitters on hydraulic and anti-clogging performance[J].Transactions of the ASABE，2006，49(3)：637-643.

6 张俊. 迷宫流道灌水器水力与抗堵性能评价及结构优化研究[D]. 西安：西安交通大学, 2009.

7 谢巧丽，牛文全，李连忠.迷宫流道转角与齿间距对滴头性能的影响[J].排灌机械工程学报，2013，31(5)：449-455. XIE Qiaoli，NIU Wenquan，LI Lianzhong. Effect of tooth angle and pitch of labyrinth channel on performance of emitter[J]. Journal of Drainage and Irrigation Machinery Engineering，2013，31(5)：449-455. (in Chinese)

8 王文娥,王福军,牛文全,等.滴头流道结构对悬浮颗粒分布影响的数值分析[J].农业工程学报，2009,25(5):1-6. WANG Wen’e,WANG Fujun,NIU Wenquan, et al.Numerical analysis of influence of emitter channel structure on suspended granule distribution[J]. Transactions of the CSAE,2009,25(5):1-6.(in Chinese)

9 魏正英，赵万华，唐一平.滴灌灌水器迷宫流道主舫道抗堵设计方法研究[J].农业工程学报，2005，21(6)：1-7. WEI Zhengying, ZHAO Wanhua, TANG Yiping. Anti-clogging design method for the labyrinth channels of drip irrigation emitters[J]. Transactions of the CSAE, 2005,21(6): 1-7. (in Chinese)

10 孟桂祥，张鸣远,赵万华，等.滴灌滴头内流场的数值模拟及流道优化设计[J].西安交通大学学报,2004,38(9):920-924. MENG Guixiang，ZHANG Mingyuan，ZHAO Wanhua，et al. Numerical flow simulation and optimum channel design of drip irrigation emitter[J].Journal of Xi’an Jiaotong University,2004,38(9):920-924. (in Chinese)

11 PAULAU S, ARVIZA V G, BRALTS J V F. Hydraulic flow behavior through an in-line emitter labyrinth using CFD techniques[C]∥2004 ASAE Annual Meeting, ASAE Paper 042252,2004.

12 王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京：清华大学出版社, 2004.

13 唐学林,余欣,任松长,等.固-液两相流体动力学及其在水力机械中的应用[M]. 郑州：黄河水利出版社,2006.

14 喻黎明，谭弘，常留红，等. 基于CFD-DEM耦合的迷宫流道水沙运动数值模拟[J/OL].农业机械学报，2016,47(8):65-71. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160810&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2016.08.010. YU Liming，TAN Hong，CHANG Liuhong，et al．Numerical simulation of water and sediment flow in labyrinth channel based on coupled CFD-DEM [J/OL]．Transactions of the Chinese Society for Agricultural Machinery，2016,47(8):65-71. (in Chinese)

15 CHU K W, WANG B, YU A B, et al. CFD-DEM modelling of multiphase flow in dense medium cyclones[J]. Powder Technology, 2009, 193(3):235-247.

16 QIU L H, WU C Y. A hybrid DEM/CFD approach for solid-liquid flows[J]. Journal of Hydrodynamics,Ser.B,2014,26(1):19-25.

17 王国强，郝万军,王维新.离散单元法及其在EDEM上的实践[M].西安：西北工业大学出社，2010.

18 喻黎明. 结构参数对梯形流道水力性能及抗堵塞性能的影响[J].西北农林科技大学学报:自然科学版，2011,39(8):197-202. YU Liming. Influence of the structural parameters of trapezoidal-channel emitters on hydraulic and anti-clogging performance[J].Journal of Northwest A&F University:Nat.Sci.Ed.，2011,39(8)：197-202.(in Chinese)

19 魏正英，唐一平，温聚英，等 灌水器细微流道水沙两相流分析和微PIV及抗堵试验研究[J].农业工程学报，2008，24(6)：1-9. WEI Zhengying，TANG Yiping，WEN Juying，et al. Two-phase flow analysis and experimental investigation of miero-PIV and anti-clogging for micro-channels of emitter[J]. Transactions of the CSAE，2008,24(6)：1-9.(in Chinese)

20 喻黎明，吴普特，牛文全，等. 迷宫流道内固体颗粒运动的CFD模拟及PIV验证[J].农业机械学报，2009,40(5):45-51. YU Liming，WU Pute，NIU Wenquan，et al. CFD Numerical simulation and PIV verification about the movement of solid particles in labyrinth channel[J]．Transactions of the Chinese Society for Agricultural Machinery，2009，40(5)：45-51．(in Chinese)

Influence of Geometrical Parameters of Labyrinth Passage of Drip Irrigation Emitter on Sand Movement

YU Liming1XU Xia2YANG Qiliang1WU Yongdong3BAI Xiaojun3

(1.FacultyofModernAgriculturalEngineering,KunmingUniversityofScienceandTechnology,Kunming650500,China2.SchoolofHydraulicEngineering,ChangshaUniversityofScience&Technology,Changsha410114,China3.QinghaiProvincialWaterConservancyandHydropowerSurveyandDesignInstitute,Xining810001,China)

In order to obtain the optimum geometrical parameters for improving the anti-clogging performance of labyrinth flow path of drip emitter,16 kinds of flow paths were designed according to the structural parameters such as angle, height, upper base, offset and width. An Eulerian-Lagrange liquid-solid multiphase turbulence model combined with the kinetic theory of granular flow was used to carry out simulation based on coupled CFD-DEM water-sand two-phase flow in drip irrigation emitter, which analyzed the pass rate of sand group, the percentage decrease in speed of sand, the movement and distribution regulars and force and so on. The result indicated that the clogging performance of labyrinth channel could be expressed by the pass rate of sand. There existed a negative relationship between the pass rate and percentage drop of sand group speed . The speed descending of sand movement was the key factor that affected the sand pass rate in labyrinth channel. The angle and width were the main structural parameters of flow passage that affected the water flow characteristics. The speed of sand particles depended on the flow characteristics of the flow channel, and the angle had a significant influence on sand speed. Sand was always drawn by drag force from water flow in the optimum structure. Most of the sand ran in the mainstream area, so they maintained high movement speed. Little sand lost kinetic energy, thereby it reduced the blocking probability. This method was applied to analyze movement and distribution of sand group, understand the movement of sand from micro-view perspective, and it had become an efficient technique in structural design of labyrinth channel.

drip irrigation emitter； labyrinth channel； structural parameters； numerical simulation； pass rate

10.6041/j.issn.1000-1298.2017.02.034

2016-11-20

2016-12-12

国家自然科学基金项目(51379024)

喻黎明(1976—)，男，副教授，博士，主要从事节水灌溉理论研究，E-mail： liming16900@sina.com

杨启良(1978—)，男，教授，博士，主要从事节水灌溉理论与技术研究，E-mail： yangqilianglovena@163.com

S275.6

A

1000-1298(2017)02-0255-07