Meyer小波在电力系统谐波检测中的应用

杨超，唐平，孙锋

(国电南京自动化股份有限公司，南京 210003)

Meyer小波在电力系统谐波检测中的应用

杨超，唐平，孙锋

(国电南京自动化股份有限公司，南京 210003)

目前所采用的小波基函数和快速傅里叶变换算法对谐波信号进行检测分析时存在频带混叠、泄漏现象，使检测出的谐波存在较大的误差，提出了运用具有无限可导性、双正交性和无频带混叠现象的Meyer小波基函数对谐波信号进行小波分解，进而进行准确检测、识别定位的新方法。运用该方法对谐波信号进行仿真试验，并将仿真结果与用db3小波基分析的结果进行了比较，验证了该方法的准确性。

电能质量；谐波检测；小波分析；Meyer小波

0 引言

随着电力系统的快速发展，电网容量和体系结构变得越来越复杂，大量的非线性负载广泛应用，导致电网中电能质量严重受损。谐波污染是比较突出的问题之一，直接降低了电能在生产、输送和利用中的效率，同时也加快了电气设备的绝缘老化，大大缩短了其使用寿命，甚至给电网的安全稳定运行带来一定的影响[1-4]。对谐波信号的检测不仅局限于检测出电网中各次谐波及其所占的比例，还要对其进行准确定位，为谐波的综合治理打下基础。

目前，快速傅里叶变换(FFT)及其改进算法和采用频域有频带混叠现象的小波基函数是使用最为广泛的谐波分析方法。电网有其自身的复杂性，电网中的负载均处于随机变化中，使得电网中电压和电流波形具有时变非平稳的特性。作为现代信号处理非常强有力的工具，小波变换能够很好地在局域中完成时间与频率之间的快速变换，并且在信息提取上十分高效；然而，如果采用频域有频带混叠现象的小波基函数，也会使谐波信号在检测和定位上产生一定误差[5-12]。参考大量的国内外文献资料，采用基于Meyer函数的小波基函数可以解决以上问题。

这里提出了一种基于Meyer小波的谐波检测方法。Meyer小波基函数收敛速度快，又具有无限可导性和双正交性，在频率支撑区间的宽度仅约为2，而频窗中心的宽度为7，远远满足了频域不产生混叠的条件[13]。基于以上特点，使用该分析方法不仅可以检测出含有的各次谐波，提高谐波测量的精准度，同时还可对各次谐波信号产生的时刻和持续时间做出准确判断。最后仿真分析了稳态和暂态两种状态谐波信号，仿真结果验证了该分析方法的可行性。

1 基于Meyer小波的谐波分析方法

1.1 小波基的选择

提取电力系统瞬态干扰的特征时，选用不同的小波函数对检测结果的准确性和有效性影响比较大，Meyer小波的正交性使分解后的各尺度间没有冗余的信息，对称性保证了相位很好的线性，时域的紧支撑保证了时间特性，而频域的紧支撑使得信号的频域划分得更为严格，因而在检测谐波信号时，Meyer小波可以清晰地划分出各频带，且各频带信号之间不会互相影响产生混叠。Meyer函数是通过频域来定义的，即

式中：v(x)为辅助函数，v(x)=x4(35-84x+70x2-20x3)，x∈(0,1) 。

1.2 小波多分辨率分析

对谐波信号进行多分辨率分析

图1 低频近似信号序列和高频细节信号序列

式中：h为低通滤波器，g为高通滤波器，不同的小波基对应不同的高、低通滤波器；aj(n)为信号的低频部分，也称为离散近似信号；dj(n)为信号的高频部分，也称为离散细节信号；n为滤波器组中滤波器系数的个数；k为小波分解的尺度，k=2j；j为分解层数。

在分解过程中，aj(n)和dj(n)构成了原始信号信息。在下一层分解中，将aj(n)分解成低频aj+1(n)和高频dj+1(n)两部分，aj+1(n)和dj+1(n)则组成aj(n)信号。如此类推，不同频带上的信号分量就被分解出来了，信号的精细程度与分解层数成正比。在本方法的分解过程中，如果某一频段上的小波变换系数出现模的极大值，则继续对该频段进行多分辨率分析，直到将所有谐波信号在不同的频段全部分解出来为止。

1.3 分解层数的确定

在对频带进行划分的过程中，基频信号必须保证落在最低子频带的中心。本文分析的谐波信号的基频fr为50 Hz的N倍的信号(其中N为正整数)，因而对应的最低子频带应为0～100 Hz。在本文中，每个周波的采样点N=128，则采样频率fs=Nfr=6 400Hz。根据香农采样定理，得到h=N/2-1=63，即为最高检测谐波次数，满足GB14549—1993《电能质量 公用电网谐波》中对谐波分析的要求。根据最低子频带0～100Hz的范围，可以确定其他频带的范围依次为100～200Hz，200～400Hz，400～800Hz，800～1 600Hz，1 600～3 200Hz，由此可知，本文的分解层数为5层。在实际检测分析过程中，如果其中一个频带中出现了小波系数模的极大值，将继续对这一频带进行精细划分。

2 仿真结果

模拟在基波频率为50Hz、有效值为220V的电压信号中存在谐波信号，来验证所采用分析方法的准确性和有效性。

2.1 稳态谐波信号仿真

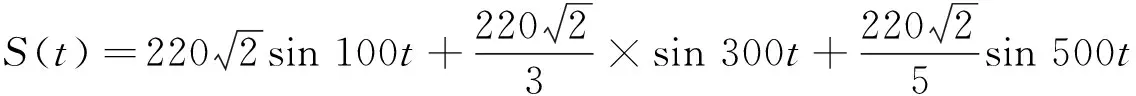
由多分辨分析的性质可知：S(t)=a5+d5+d4+d3+d2+d1，其中：a5对应0～100Hz的子频段，d5对应100～200 Hz的子频段，d4对应200～400 Hz的子频段，d3对应400～800 Hz的子频段，d2对应800～1 600 Hz的子频段，d1对应1 600～3 200 Hz的子频段。从图1可以看出，使用Meyer小波分析法分解、重构给定的信号之后，能够有效提取出各谐波信号，给定信号所包含的50，150，250 Hz信号分别落在了a5，d5和d4对应的子频带中，而d3，d2以及d1对应的子频带中高频细节信号几乎为0。由此可见，使用本方法对谐波信号进行检测时，避免了频谱混叠、泄漏的现象，保证了谐波信号检测的有效性。表1是谐波引起电网波形畸变程度的畸变指标理论值和测量值的比较，从表1可以更直观地看出本文采用的分析方法对谐波信号检测的准确性。

表1 畸变指标的理论值和测量值的比较

图2 Meyer小波处理含暂态谐波的电网信号的结果

2.2 暂态谐波信号仿真

当某一子频带上有局部模极大值出现时，电网信号S(t)在这一子频带上发生了突变，简而言之，小波系数模的极大值点位置可以快速准确地确定谐波信号产生的起止时刻。根据发生时刻及其持续时间，能够有针对性地找到快速有效的治理措施，避免严重事故的发生。给出一电网电压信号S(t)，一个有效值为44 V的5次谐波信号发生在该信号的0.02～0.08 s时段。通过多分辨率分析，高频细节信号序列d1和d2捕捉了谐波信号发生的时刻和结束的时刻。图2为用Meyer小波处理该信号的结果。

由图2可知，本方法能够高效地提取出基波和暂态的5次谐波，而且在高频细节信号序列d1和d2中2个突变点处小波系数很大，突变点之间的小波系数为0。表2比较了谐波产生时间的理论值和测量值之间的误差，根据比较结果可以看出，基于Meyer小波的分析方法能够快速精准地完成谐波定位。

2.3 db3小波处理稳态谐波信号仿真结果

对2.1节中给定的信号采用db3小波进行分析，db系列小波的特点是随着阶次的增大，频带的划分效果越来越好，但是时域的支撑性逐渐减弱，同时分析计算的运算量也大大增加，使得分析的实时性变差。因此，在进行阶次选择时，不但要注重算法本身的效果，还应兼顾算法的效率。以本文为例，在对电网的谐波分析中，经过大量的实验分析比较发现，阶数较大的db系列小波，如db20等，在进行电力系统谐波分析时，虽然具有更好的频带划分效果，但计算时间显著增加，达不到实时检测的要求；为了具有相对较好的频带划分效果和时域的紧支持性，同时兼顾算法本身的效果和效率，选取了db系列的db3小波，检测结果如图3所示。由图3可以看出：基波和谐波发生了非常明显的频谱泄漏，存在比较大的误差，无法实现精准检测。

表2 谐波信号产生时间的理论值和测量值的比较

2.4 db3小波处理暂态谐波信号仿真结果

与2.2节中所用信号一致，db3小波对暂态谐波的检测结果如图4所示，显示出了d1和d2的高频细节信号序列，图中检测出的暂态谐波发生的时间为0.019 5 s，结束的时间为0.079 0 s，持续时间为0.059 5 s，与理论值之间的误差分别为2.50%，1.25%以及0. 83%，远大于本文给出的检测方法的误差。

图3 db3小波处理含稳态谐波的电网信号的结果

图4 db3小波处理含暂态谐波的电网信号的结果

3 结论

本文给出了一个检测公用电网中谐波信号的简单、有效、准确的分析方法，通过MATLAB的具体仿真可以看出，利用此方法对公用电网信号进行分析，可以有效地提取信号的基频分量和各次谐波分量并实时跟踪谐波的变化，达到识别和定位各次谐波的目的。相对于传统的谐波检测分析方法，此方法在快速准确定位谐波信号的起始点和终止点上具有较高的准确性，从而使其在电力系统谐波信号分析检测中具有很广的应用前景。

[1]陈鹏伟,肖湘宁,陶顺.直流微网电能质量问题探讨[J].电力系统自动化,2016,40(10):148-158.

[2]林海雪.电力系统的间谐波来源及其影响[J].电源技术应用，2010，13(5)：1-6.

[3]KURAISHI T,KAWADA M,ISAKA K.Development of recursive interpolated D/FFT for on-line and highly accurate frequency analysis[J].IEEJ transactions on electrical and electronic engineering,2008,3(5):574-582.

[4]刘书铭，李琼林，余晓鹏，等.谐波强度对电容器损耗影响的试验研究[J].电力自动化设备，2014，34(5):169-173.

[5]蒋玮，陈武，胡仁杰.基于超级电容器储能的微网统一电能质量调节器[J].电力自动化设备，2014，34(1)：85-90.

[6]WANG H,LI Q N,WU M L.Investigation on a new algorithm for instantaneous reactive and harmonic currents detection applied to intensive nonlinear loads[J].IEEE transactions on power delivery，2007,22(4):2312-2318.

[7]CHANG Y P,LOW C.Optimization of a passive harmonic filter based on the neural-genetic algorithm with fuzzy logic for a steel manufacturing plant[J].Expert systems with applications,2008,34(3):2059-2070.

[8]熊杰锋,李群,袁晓冬,等.电力系统谐波和间谐波检测方法综述[J].电力系统自动化,2013,37(11):125-133.

[9]金维刚，刘会金.IEC标准框架下谐波和间谐波检测的最优化方法[J].电力系统自动化,2012,36(2):70-76.

[10]NING J X, WANG J H, GAO W Z,et al.A wavelet-based data compression technique for smart grid[J].IEEE transactions on smart grid,2011,2(1):212-218.

[11]贾毅婷，张东来，张斌.基于小波尺度相关性的暂态数据降噪压缩方法[J].电力系统自动化,2013,37(5):68-73.

[12]NASSIF A B，JING Y，MAZIN H，et al.An impedance-based approach for identifying interharmonic sources [J].IEEE transactions on power delivery，2011，26(1)：333-340.

[13]雷何，高山，林新春，等.基于包含谐波模型的加权最小二乘估计算法的电压暂降检测方法[J].电力自动化设备，2013，33(9)：36-41.

(本文责编：刘芳)

2016-07-18；

2016-11-14

TM 930.12

A

1674-1951(2017)01-0001-04

杨超(1985—)，男，江苏建湖人，工程师，工学硕士，从事电能质量在线监测方面的研究(E-mail:yc_kx0323@qq.com)。