135°弯管内硫浆输送的数值模拟
孙芳芳 Muhammad Adnan 张 楠 宋 彬 李映年 吴 宇 刘 蔷
1.中国矿业大学(北京)资源与安全工程学院 2.中国科学院过程工程研究所多相复杂系统国家重点实验室 3.中国科学院大学 4. 中国石油西南油气田公司天然气研究院
135°弯管内硫浆输送的数值模拟
孙芳芳1,2Muhammad Adnan2,3张 楠2宋 彬4李映年4吴 宇4刘 蔷4
1.中国矿业大学(北京)资源与安全工程学院 2.中国科学院过程工程研究所多相复杂系统国家重点实验室 3.中国科学院大学 4. 中国石油西南油气田公司天然气研究院
采用欧拉-欧拉法,对硫浆在135°弯管内的流动状态进行数值模拟。通过和Toda实验的90°弯头对比进行模型的验证。验证结果表明,模拟值和实验值吻合良好。对相同操作条件下45°和90°弯头的压降进行了比较分析,分析了硫浆体积分数和硫浆速度对弯头压降的影响。同时,研究了硫浆体积分数和硫浆速度对135°弯管内流动状态的影响。对本研究所针对的管道而言,当硫浆体积分数为0.15时,建议输送速度大于1.2 m/s。
液固两相流 数值模拟 欧拉-欧拉模型 弯头压降 硫浆输送
液固两相流水力管道输送系统广泛应用于化工、矿业、能源、环保等领域。由于工业输送的需要,两相流输送管道通常由弯头连接。弯头内两相流流动复杂,会给管道造成额外的问题,如附加压降、冲蚀、磨损和堵塞等。
已有大量研究人员进行了浆体输送的研究,Abulnaga[1]综述了浆体不淤速度的计算方法。Wasp[2]提出流型分类标准,把浆体在管道中的运动分为均质流、非均质流和介于两者之间的均质-非均质复合流3种流态。为保证浆体正常输送,研究人员通过理论研究和实验手段分析浆体输送的不淤速度和压降。刘弦[3]通过90°弯管内输送颗粒的受力分析,得到了颗粒沉降速度和两相流临界速度的表达式,可以给出物料密度、弯管半径、两相流黏度和浓度对两相流临界速度的影响。Toda[4]通过实验测定水平和垂直90°弯头的压降情况,分析了速度和浓度对90°弯头压降的影响。研究表明,在垂直90°弯头内,两相流弯头附加压降与两相流平均速度的平方呈正比,这种趋势与水平90°弯头趋势相似,但受颗粒性质和弯头参数的影响,具体参数不同。
随着计算机模拟技术的发展和液固两相流理论基础的完善,CFD(Computational Fluid Dynamics,计算流体力学)研究两相流内流态的分布和发展变化被广泛应用,它克服了实验周期长、经费高的缺点,成为研究两相流运动的有效手段。Hu[5]采用直接数值模拟研究了垂直管道内的液固两相流。王继红[6]采用欧拉-欧拉模型对水平管道内液固两相流进行模拟,研究表明,曳力和湍流扩散力是两相间动量传递的主要影响因素。有研究人员探索改变弯头角度,以减少弯头处的磨损和阻力损失。例如,张少峰[7]利用欧拉-拉格朗日方法模拟了60°~120°弯管内的气固两相流颗粒的运动状态、压力分布和磨损情况。于飞[8]采用DPM(Discrete Phase Model,离散项模型)分析了15°~90°转角时的磨损和阻力损失。结果表明,为了达到减磨、降阻的效果,最好用转角小于60°的锐角弯头代替90°弯头,并且转弯角度越小越好。
前述文献所涉及的大多为水平弯管或垂直90°弯管,而对非90°垂直弯管内的流动研究较少。本研究采用欧拉-欧拉模型模拟了带有45°标准弯头的垂直方向为135°管道内液固两相流的流动状态和压降情况,并讨论了硫浆浓度、硫浆速度对压降和流动状态的影响。
1 数学模型
本研究采用欧拉-欧拉双流体模型,将液固两相视为互相贯穿的连续体。通过Navier-Stokes方程求解两相的质量和动量方程,湍流选用标准k-ε模型[9]。液固两相间动量传递最主要的力是曳力,因而本研究只考虑曳力作用。根据郭慕孙等[10]提出的流态化类型,液固两相输送主要是散式流态化,因此,本研究采用Gidaspow曳力模型[11]。
2 几何结构和网格
2.1 几何结构
讨论液固两相流在带有45°标准弯头的135°弯管中的流动,其几何结构如图1所示。管道内径为0.055 m,水平段长度为1 m,倾斜段长度为4 m,弯头为45°长半径弯头。浆体从水平管进入管道,经过弯头输送向倾斜管,并由倾斜管顶部流出。图1中,A-A截面为水平管0.5 m处,B-B截面为弯头中心,C-C截面为倾斜管道1 m处,D-D截面为倾斜管道2 m处,E-E截面为倾斜管道4 m处,即出口处。

2.2 模型与求解
本研究所模拟的液体密度为1 050 kg/m3,黏度为9.28×10-4Pa·s,硫浆颗粒密度为1 960 kg/m3,颗粒直径为50 μm。硫浆体积分数为0.1~0.3,硫浆速度为0.6~4.7 m/s。采用速度入口、压力出口边界条件。液相壁面设置为无滑移,固相壁面设置为部分滑移边界条件。采用压力-速度修正的SIMPLER算法。首先进行了稳态与非稳态的对比,发现稳态与非稳态模拟得到的压降和颗粒质量流率差别不大,为节省计算时间和计算资源,采用稳态求解。
3 结果和讨论
3.1 网格无关性验证和模型验证
采用5 mm、10 mm、20 mm的六面体网格进行网格无关性验证。对于不同的网格尺寸,颗粒流率和压降变化不大。兼顾计算资源的需求和计算精度,本研究选用10 mm网格。
由于缺少135°弯管的液固实验数据,选取Toda[4]所做的垂直90°弯管内液固实验进行模型验证。在Toda[4]的90°弯管液固实验中,管道直径为30.2 mm,弯头曲率半径为240 mm,水平管道长度为1 m,垂直管道长度为4 m。实验颗粒直径为0.99 mm,颗粒密度为2 500 kg/m3,颗粒质量分数3%~5%。本研究使用与Toda实验相同的几何结构和条件,对颗粒质量分数分别为3%和5%进行了模拟,弯头出入口压降结果见图2。从图2可以看出,使用模型预测的弯头压降随速度增加的趋势与实验值一致,实验数据大部分位于模拟的颗粒质量分数3%~5%之间,因而后续采用所选模型对135°弯管内液固流动进行模拟研究。

3.2 压力场分析
在管道设计和浆体输送过程中,压降是一个重要参数。在输送系统水平方向,造成压降的主要因素是摩擦力,在垂直方向是对颗粒质量的承载与颗粒势能的转换。本研究采用与135°弯管相同的结构模拟90°弯管内的流动,对比了90°和135°弯管内的压降情况。硫浆体积分数为0.15,硫浆速度为1.2 m/s时,90°和135°弯管内压降如图3所示。

从图3可以看出,在水平管段,90°和135°管道压降基本相同。在弯头段,90°的弯头压降大于连接135°管道的45°弯头。相比90°管道,在135°倾斜管道内,壁面对流体和颗粒有一定的支撑作用,因而,135°管道压降的沿流动方向的斜率小于90°管道。
3.2.1 硫浆速度对弯头压降的影响
Ahmed[12]给出了水平90°长半径弯头的局部压降公式,见式(1)。
(1)
式中:Δpb为弯头压降,Pa;Kb是弯头压损常数,无量纲;ρm为浆体密度,kg/m3;vm为浆体速度,m/s;g为重力加速度,m/s2,其值取9.81。
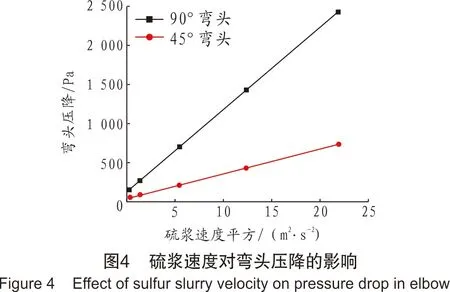
图4是硫浆体积分数为0.15时,硫浆速度对弯头压降的影响。从图4可以看出,45°和90°弯头压降均随硫浆速度增大而增大,与速度平方呈正比,这与Ahmed[12]的结论一致。由于弯头参数不同,采用上述公式计算的压降与模拟的压降数值不同。通过数值拟合,本研究中45°弯头和90°弯头的Kb值分别为0.06和0.12。
3.2.2 硫浆体积分数对弯头压降的影响
图5是硫浆速度为1.2 m/s时,硫浆体积分数对45°和90°弯头压降的影响。

由图5可知,在45°和90°弯头内,压降均随硫浆体积分数的增加而增加,并与硫浆体积分数成正比。硫浆体积分数增加,使弯头内颗粒数目增多,颗粒质量增大。同时,颗粒与颗粒之间以及颗粒与管壁之间的碰撞增强,耗散能量增加,因而压降增大。在相同的操作条件下,90°弯头内的压降大于45°弯头,这与董志勇[13]对于不同角度弯头内压降的研究结果一致。
3.3 速度分布
图6显示的是入口硫浆速度为1.2 m/s时,不同硫浆体积分数所对应的不同位置的截面中心速度分布情况。r0/D等于0,是弯管外壁,r0/D等于1,是弯管内壁。如图6所示,不同位置处速度分布差别很大。从图6(a)可以看出,弯头内速度呈现明显的不对称分布,内壁颗粒速度明显大于弯管外壁。这是由于在弯头处由于离心力的作用,颗粒向外壁处聚集,使得弯管外壁比内壁颗粒浓度高,流道变窄,相应内壁处颗粒速度增大。随着硫浆体积分数的增大,这种不均匀更加明显。从图6(b)~图6(d)可以看出,在倾斜管段,速度分布的对称性明显优于弯头处,管道中心处颗粒速度大,管壁处颗粒速度小。随着硫浆体积分数的增大,倾斜管的速度分布趋于平缓。在倾斜管道下部,颗粒速度最大的位置在管道轴线位置以下,而在管道上部,颗粒速度最大位置已基本恢复到管道轴线位置。
3.4 浓度分布
图7显示的是入口硫浆体积分数为0.15时,在不同硫浆速度下135°弯管内的体积分数分布。从图7可以看出,当vl=0.6 m/s时,管道内体积分数分布出现了明显的分层现象,并且这样的分层现象在弯头内和倾斜管段更加明显。随着流速的增大,管道截面的体积分数分布趋于均匀。
Wasp[2]提出管道内浆体分类标准,用C/CA比值来表征,其中C是管顶下0.08倍直径处的体积分数,CA是管中心处的体积分数。当C/CA≥0.8时,浆体呈均质性;当C/CA≤0.1时,浆体呈非均质性;当0.1 从图8可以看出,当vl=0.6 m/s时,弯头中心位置的C/CA>0.8,此处浆体呈现均质流,弯管出口位置的C/CA=0.73,介于0.1与0.8之间,此处浆体介于均质流与非均质流之间。当vl大于1.2 m/s时,弯头中心位置和弯管出口位置的C/CA均大于0.8,浆体呈现显著的均质流。随着硫浆速度增大,管道内流型更加均匀。另外,当vl>0.88 m/s时,C/CA大于0.8,而通过Wasp[14-15]公式计算的浆体不淤速度为1.16 m/s。综合流型分类与浆体不淤速度的研究,为了保证安全稳定输送,推荐硫浆入口速度大于1.2 m/s。 本研究采用欧拉-欧拉模型模拟了135°弯管内液固两相流的流动状态,并分析了影响液固浆体输送的关键因素。结论如下: (1) 弯头处液固两相流出现明显的分层现象,不同速度下固体颗粒均集中向弯头外壁运动,导致外壁处颗粒浓度高,同时弯头外壁颗粒速度低,因而在弯头处容易发生淤堵。 (2) 硫浆体积分数增大,压降增大,压降和硫浆体积分数呈正比。 (3) 硫浆速度增大,压降增大,压降与硫浆速度平方呈正比。 (4) 结合Wasp不淤速度公式和流型分类,对于本研究所针对的管道,当硫浆体积分数为0.15时,建议输送速度大于1.2 m/s。 [1] ABULNAGA B E. Slurry systems handbook[M]. New York: McGraw-Hill, 2002. [2] 瓦斯普. 固体物料的浆体管道输送[M]. 北京: 水利出版社, 1980. [3] 刘弦. 90°弯管内固液两相流临界流速浅析[J]. 工程建设与设计, 2007(2): 41-44. [4] TODA M, KOMORI N, SAITO S, et al. Hydraulic conveying of solids through pipe bends[J]. Journal of Chemical Engineering of Japan, 1972, 5(1): 4-13. [5] HU H H. Direct simulation of flows of solid-liquid mixtures[J]. International Journal of Multiphase Flow, 1996, 22(2): 335-352. [6] 王继红, 张腾飞, 王树刚, 等. 水平管道内固液两相流流动特性的CFD模拟[J]. 化工学报, 2011, 62(12): 3399-3404. [7] 张少峰, 曹会敏, 刘燕, 等. 弯管中液固两相流及壁面碰撞磨损的数值模拟[J]. 河北工业大学学报, 2008, 37(3): 48-54. [8] 于飞, 刘明, 王汀, 等. 弯头内气-固两相流动与管壁磨损特性研究[J]. 工程热物理学报, 2015, 36(4): 796-800. [9] LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence[M]. London: Academic Press, 1972. [10] 郭慕孙, 李洪钟. 流态化手册[M]. 北京: 化学工业出版社, 2008: 154. [11] GIDASPOW D. Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. London: Academic Press, 1994. [12] AHMED M, SINGH S N, SESHADRI V. Pressure drop in a long radius 90° horizontal bend for the flow of multi-sized heterogeneous slurries[J]. International Journal of Multiphase Flow, 1994, 21(2): 329-334. [13] 董志勇. 弯头(弯管)阻力系数比较与流动特性分析[C]//第五届全国水动力学学术会议暨第十五届全国水动力学研讨会文集. 2001, 北京. [14] WASP E J, KENNY J P, GANDHI R L. Solid Liquid Flow Slurry Pipeline Transportation[M]. Clausthal, Germany :Trans. Tech. Publications, 1977. [15] KAUSHAL D R, TOMITA Y, DIGHADE R R. Concentration at the pipe bottom at deposition velocity for transportation of commercial slurries through pipeline[J]. Powder Technology, 2002, 125(1): 89-101. Numerical simulation of sulfur slurry transportation in a 135° bend pipe Sun Fangfang1,2, Muhammad Adnan2,3, Zhang Nan2, Song Bin4, Li Yingnian4, Wu Yu4, Liu Qiang4 1.SchoolofResourcesandSafetyEngineering,ChinaUniversityofMining&Technology(Beijing),Beijing,China; 2.StateKeyLaboratoryofMultiphaseComplexSystems,InstituteofProcessEngineering,ChineseAcademyofSciences,Beijing,China; 3.UniversityofChineseAcademyofSciences,Beijing,China; 4.ResearchInstituteofNaturalGasTechnology,PetroChinaSouthwestOil&GasfieldCompany,Chengdu,Sichuan,China A numerical simulation study for flow behavior of sulfur slurry in 135° bend pipe has been conducted by Eulerian-Eulerian model. Validation of the models could be obtained from the comparison with a 90° elbow of Toda. The predicted results were in good agreement with experimental data. A general comparison of pressure drop in the 45° and 90° elbow were also discussed in present research at the same operating condition as a reference. The effects of the sulfur slurry volume fraction and sulfur slurry velocity on the pressure drop in elbow as well as on the flow characteristics in 135° bend were studied. In present research, when the sulfur slurry volume fraction was 0.15, the minimum transport velocity was proposed to be higher than 1.2 m/s. liquid-solid two-phase flow, numerical simulation, Euler-Euler model, pressure drop in bend, transportation of sulfur slurries 孙芳芳(1990-),女,河南平顶山人,中国矿业大学(北京)硕士研究生。E-mail: ffsun@ipe.ac.cn TE646; TQ015.9; TP391.9; O6-39 A 10.3969/j.issn.1007-3426.2017.01.005 2016-08-22;编辑:温冬云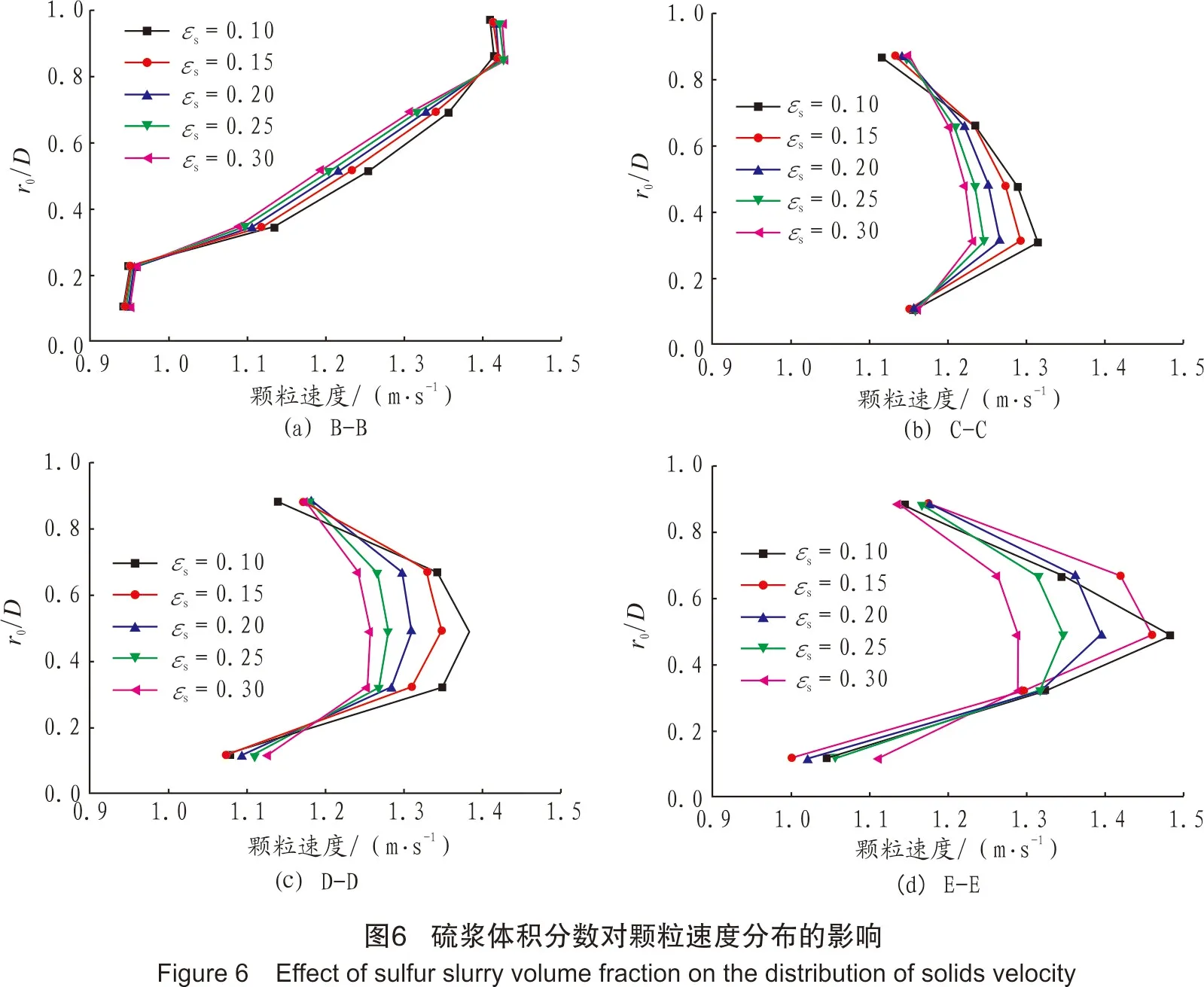


4 结 论

